2020-2021学年苏科版七年级数学下册第8章幂的运算复习课件(25张)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册第8章幂的运算复习课件(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 893.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 15:59:37 | ||
图片预览





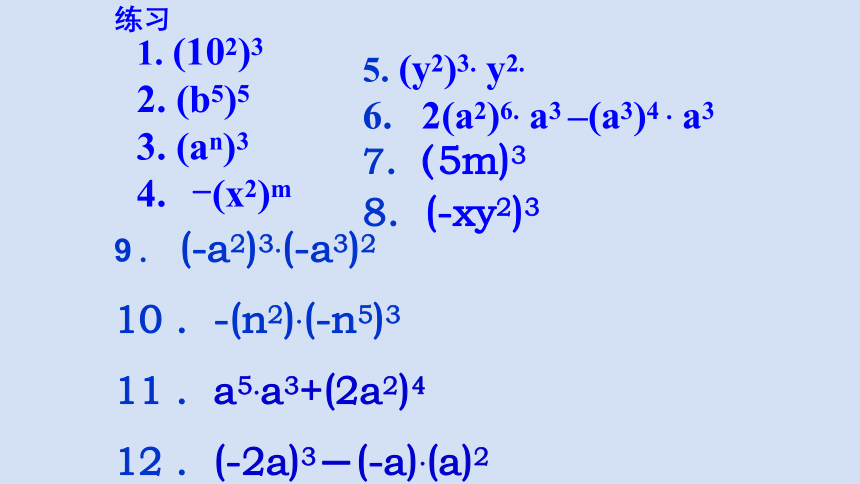


文档简介
2021
第八章 幂的运算复习
苏科版七年级下册 数学
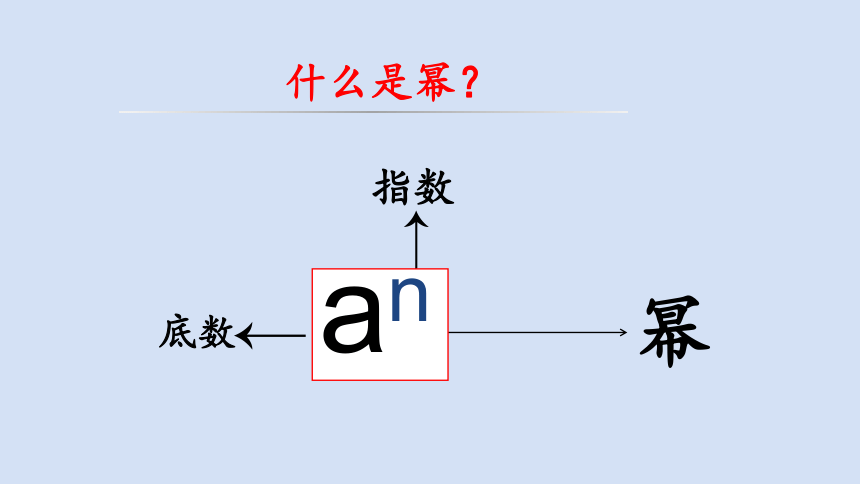
什么是幂?
→
指数
←
底数
幂
an
1.同底数幂的乘法法则
文字叙述:
同底数幂相乘,底数不变,指数相加
字母表示:
am·an=am+n (m,n是正整数)
扩展:
am·an·ap=am+n+p (m,n,p是正整数)
口答:
(1) (-8)12×(-8)5
(2) x·x7
(3) -a3·a6
a3m·a2m-1(m是正整数)
(5) a-2·a-4·a8
填空:
(1) 若a7·am=a10, m=______;
(2) xa·x3=x2a·x2,a=_______;
(3) a3·____·a2=a3;
解答:
(1) 已知:8·22m-1·23m=217,求m的值.
(2) 已知am-n=7,am+n=13,求a2m.
2.幂的乘方法则
文字叙述:
幂的乘方,底数不变,指数相乘
字母表示:
(an)m=amn (m,n是正整数)
扩展:
((an)m)p=amnp (m,n,p是正整数)
(102)3
(b5)5
(an)3
-(x2)m
5. (y2)3. y2.
6. 2(a2)6. a3 –(a3)4 . a3
练习
7.(5m)3
8. (-xy2)3
. (-a2)3.(-a3)2
10 . -(n2).(-n5)3
11 . a5.a3+(2a2)4
12 . (-2a)3-(-a).(a)2
1.若an=3,bn=5,求(1)a3n+b2n,(2)a3n·b2n的值.
2.若2x+3·3x+3=36x-2,则x的值是多少?
3.若xn=3,yn=7,则(xy)n的值是多少?(x2y3)n呢?
4.若x2n=5,求(3x3n)2-4(x2)2n 的值.
5.计算.
(1) (0.125)16×(-8)17
(2) (0.125)15×(215)3
(3) 24·45·(-0.125)4
6.(1)比较340与430的大小;
(2)比较2100与375的大小.
3.积的乘方法则
文字叙述:
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘
字母表示:
(ab)n=anbn (n是正整数)
扩展:
(abc)n=anbncn (n是正整数)
注意它的逆运算
考考你
(5a)8
(-xy3)3
(-2a3b6c2)3
-(ab3)2
(0.25)100. (4)100
(2×106)3
4.同底数幂的除法法则
文字叙述:
同底数幂相除,底数不变,指数相减
字母表示:
am÷an=am-n (a≠0 m,n是正整数 m>n)
扩展:
am÷an=am-n (a≠0 m,n是整数)
考考你
a8 ÷a3
(?)5÷(?)3
(-s)7÷(-s)2
a3 ÷a8 (a≠0)
(-3)2÷(-3)4
(-99)8 ÷(-99)8
5.零指数和负指数法则
零指数
任何不等于0的数的0次幂等于1
字母表示:
a0=1 a≠0
负指数
任何不等于0的数的-n(n是正整数)次幂,等于这个数的n次幂的倒数
字母表示:
a-p= 1/ ap = (1/a)p (a≠0)
考考你
(-0.003)0
(3x)0 (x≠0)
20170
4-2
(-4)-2
(0.1)-3
1.计算.
(1) m19÷m14·m3÷m2·m
(2) (-x2y)5÷(-x2y)3
(3) (x-y)8÷(x-y)4÷(y-x)3
(4) (-a10)3÷(-a)10÷(-a3)2÷a6
(5) (-x2n-2) ·(-x)5÷[xn+1·xn·(-x)]
(6) 98×272÷(-3)18
(7) 22-2-2+(-2)-2
(8) 4-(-2)-2-32÷(-3)0
(9) (103)2×106÷(104)3
(10) 10-2×100+103÷105
6.科学计数法
7.注意这些法则的逆向计算
一般地,
一个正(负)数可以写成±a×10n的形式,
(其中1≤a<10,n是整数)
用科学记数法表示下列各数.
(1) 360000000=____________;
(2) -2730000=_____________;
(3) 0.00000012=____________;
(4) 0.0001=________________;
(5) -0.00000000901=_________;
(6) 0.00007008=_____________.
写出下列各数的原数.
(1) 102=______________;
(2) 10-3=______________;
(3) 1.2×105=__________;
(4) 2.05×10-5=_________;
(5) 1.001×10-6=________;
(6) -3÷10-9=___________.
找错误并改正
(1) a3 .a3=2a6
(2) (a3)2=a5
(3) (xy2)3=xy6
(4) (-2b2 )2=-4b4
(5) a8÷a4=a2
(6) (-z)6÷(-z)2=-z4
1、下列算式中,①a3·a3=2a3;②10×109=1019;③(xy2)3=xy6;④a3n÷an=a3.其中错误的是( )
A、1个 B、2个 C、3个 D、4个
2、在xm-1·( )=x2m+1中,括号内应填写的代数式是( )
A、x2m B、x2m+1
C、x2m+2 D、xm+2
D
D
选一选
计算
(1) an.an+5 ÷a7 (n是整数) (2) [(x-y)3 ]0
(3) (a-b)3(a-b)5 (b-a)2 (4) (-8)55 ×0.12555
(5) -10-2-1×3-1×[2-(-3)2 ] (6) (-0.25)-1+(-2)2 ×50-0.5-2
提高应用
1、已知10m=5,10n=6,求代数式102m+3n的值
课堂小结
1、同底数幂的乘法、除法
2、幂的乘方
3、积的乘方
4、零指数和负指数
注意公式的
逆向应用
第八章 幂的运算复习
苏科版七年级下册 数学
什么是幂?
→
指数
←
底数
幂
an
1.同底数幂的乘法法则
文字叙述:
同底数幂相乘,底数不变,指数相加
字母表示:
am·an=am+n (m,n是正整数)
扩展:
am·an·ap=am+n+p (m,n,p是正整数)
口答:
(1) (-8)12×(-8)5
(2) x·x7
(3) -a3·a6
a3m·a2m-1(m是正整数)
(5) a-2·a-4·a8
填空:
(1) 若a7·am=a10, m=______;
(2) xa·x3=x2a·x2,a=_______;
(3) a3·____·a2=a3;
解答:
(1) 已知:8·22m-1·23m=217,求m的值.
(2) 已知am-n=7,am+n=13,求a2m.
2.幂的乘方法则
文字叙述:
幂的乘方,底数不变,指数相乘
字母表示:
(an)m=amn (m,n是正整数)
扩展:
((an)m)p=amnp (m,n,p是正整数)
(102)3
(b5)5
(an)3
-(x2)m
5. (y2)3. y2.
6. 2(a2)6. a3 –(a3)4 . a3
练习
7.(5m)3
8. (-xy2)3
. (-a2)3.(-a3)2
10 . -(n2).(-n5)3
11 . a5.a3+(2a2)4
12 . (-2a)3-(-a).(a)2
1.若an=3,bn=5,求(1)a3n+b2n,(2)a3n·b2n的值.
2.若2x+3·3x+3=36x-2,则x的值是多少?
3.若xn=3,yn=7,则(xy)n的值是多少?(x2y3)n呢?
4.若x2n=5,求(3x3n)2-4(x2)2n 的值.
5.计算.
(1) (0.125)16×(-8)17
(2) (0.125)15×(215)3
(3) 24·45·(-0.125)4
6.(1)比较340与430的大小;
(2)比较2100与375的大小.
3.积的乘方法则
文字叙述:
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘
字母表示:
(ab)n=anbn (n是正整数)
扩展:
(abc)n=anbncn (n是正整数)
注意它的逆运算
考考你
(5a)8
(-xy3)3
(-2a3b6c2)3
-(ab3)2
(0.25)100. (4)100
(2×106)3
4.同底数幂的除法法则
文字叙述:
同底数幂相除,底数不变,指数相减
字母表示:
am÷an=am-n (a≠0 m,n是正整数 m>n)
扩展:
am÷an=am-n (a≠0 m,n是整数)
考考你
a8 ÷a3
(?)5÷(?)3
(-s)7÷(-s)2
a3 ÷a8 (a≠0)
(-3)2÷(-3)4
(-99)8 ÷(-99)8
5.零指数和负指数法则
零指数
任何不等于0的数的0次幂等于1
字母表示:
a0=1 a≠0
负指数
任何不等于0的数的-n(n是正整数)次幂,等于这个数的n次幂的倒数
字母表示:
a-p= 1/ ap = (1/a)p (a≠0)
考考你
(-0.003)0
(3x)0 (x≠0)
20170
4-2
(-4)-2
(0.1)-3
1.计算.
(1) m19÷m14·m3÷m2·m
(2) (-x2y)5÷(-x2y)3
(3) (x-y)8÷(x-y)4÷(y-x)3
(4) (-a10)3÷(-a)10÷(-a3)2÷a6
(5) (-x2n-2) ·(-x)5÷[xn+1·xn·(-x)]
(6) 98×272÷(-3)18
(7) 22-2-2+(-2)-2
(8) 4-(-2)-2-32÷(-3)0
(9) (103)2×106÷(104)3
(10) 10-2×100+103÷105
6.科学计数法
7.注意这些法则的逆向计算
一般地,
一个正(负)数可以写成±a×10n的形式,
(其中1≤a<10,n是整数)
用科学记数法表示下列各数.
(1) 360000000=____________;
(2) -2730000=_____________;
(3) 0.00000012=____________;
(4) 0.0001=________________;
(5) -0.00000000901=_________;
(6) 0.00007008=_____________.
写出下列各数的原数.
(1) 102=______________;
(2) 10-3=______________;
(3) 1.2×105=__________;
(4) 2.05×10-5=_________;
(5) 1.001×10-6=________;
(6) -3÷10-9=___________.
找错误并改正
(1) a3 .a3=2a6
(2) (a3)2=a5
(3) (xy2)3=xy6
(4) (-2b2 )2=-4b4
(5) a8÷a4=a2
(6) (-z)6÷(-z)2=-z4
1、下列算式中,①a3·a3=2a3;②10×109=1019;③(xy2)3=xy6;④a3n÷an=a3.其中错误的是( )
A、1个 B、2个 C、3个 D、4个
2、在xm-1·( )=x2m+1中,括号内应填写的代数式是( )
A、x2m B、x2m+1
C、x2m+2 D、xm+2
D
D
选一选
计算
(1) an.an+5 ÷a7 (n是整数) (2) [(x-y)3 ]0
(3) (a-b)3(a-b)5 (b-a)2 (4) (-8)55 ×0.12555
(5) -10-2-1×3-1×[2-(-3)2 ] (6) (-0.25)-1+(-2)2 ×50-0.5-2
提高应用
1、已知10m=5,10n=6,求代数式102m+3n的值
课堂小结
1、同底数幂的乘法、除法
2、幂的乘方
3、积的乘方
4、零指数和负指数
注意公式的
逆向应用
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
