2020-2021学年人教版数学八年级下册 18.2.3 菱形及其性质 课件 (63张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册 18.2.3 菱形及其性质 课件 (63张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 16:05:15 | ||
图片预览








文档简介
第十八章
18.2.3 菱形及其性质
人教版数学八年级下册
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
温故知新
复习旧知
同学们,将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?
菱形及其性质
导入新知
学习目标
1.掌握的定义和性质及菱形面积的求法.
2.灵活运用菱形的性质解决问题.
1
知识点
菱形的定义
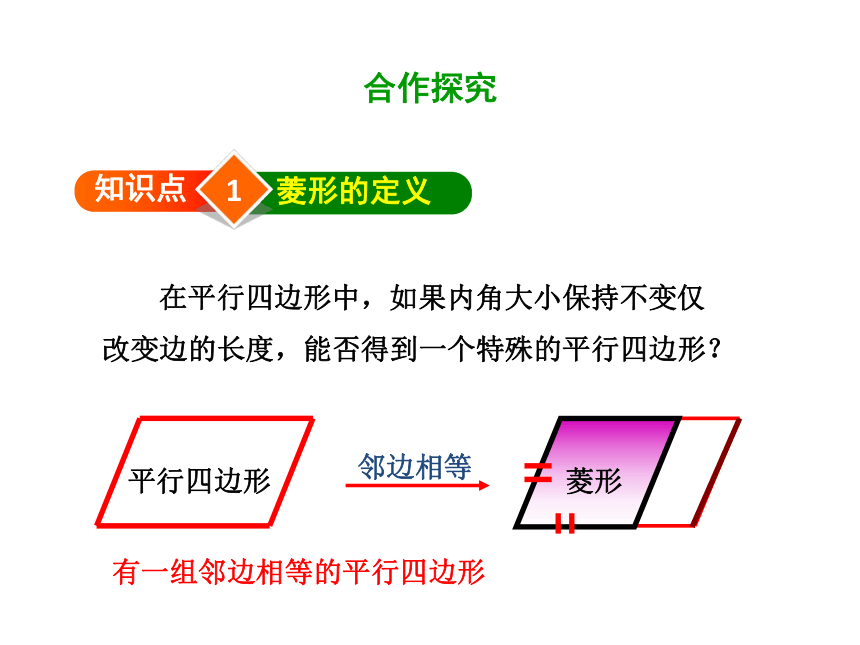
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
平行四边形
有一组邻边相等的平行四边形
菱形
邻边相等
合作探究
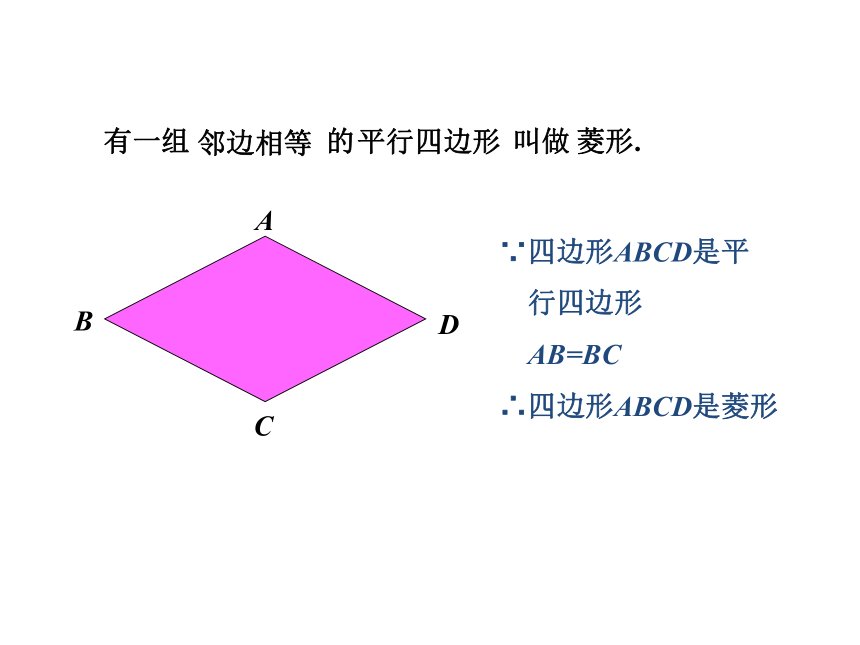
有一组 的 叫做
邻边相等
平行四边形
A
D
C
B
∵四边形ABCD是平
行四边形
AB=BC
∴四边形ABCD是菱形
菱形.
感受生活
你能举出生活中你看到的菱形吗?
生活
感受
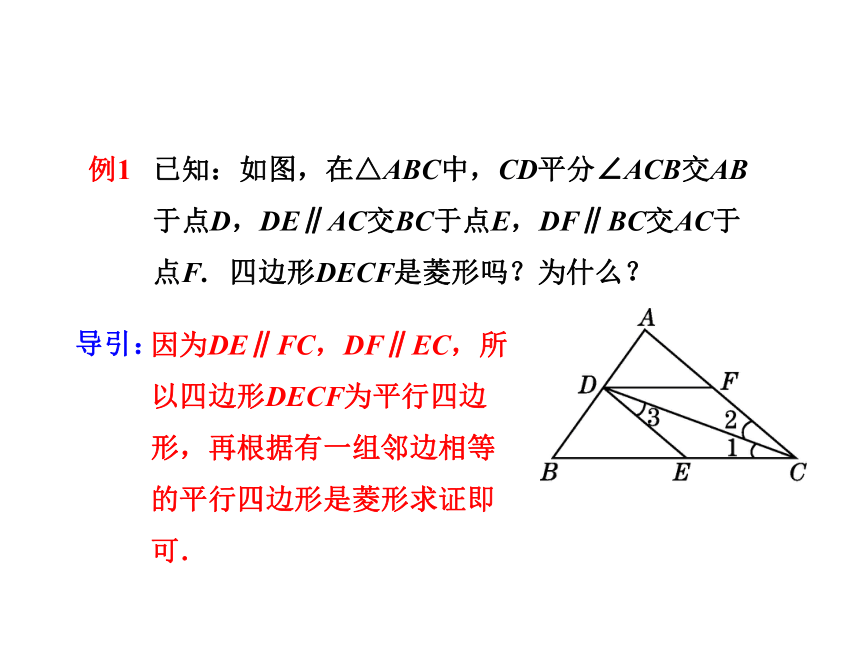
例1 已知:如图,在△ABC中,CD平分∠ACB交AB
于点D,DE∥AC交BC于点E,DF∥BC交AC于
点F. 四边形DECF是菱形吗?为什么?
因为DE∥FC,DF∥EC,所
以四边形DECF为平行四边
形,再根据有一组邻边相等
的平行四边形是菱形求证即
可.
导引:
四边形DECF是菱形.理由如下:
∵DE∥FC,DF∥EC,
∴四边形DECF为平行四边形.
由AC∥DE,知∠2=∠3.
∵CD平分∠ACB,
∴∠1=∠2,∴∠1=∠3,∴DE=EC,
∴平行四边形DECF为菱形(有一组邻边相等的平
行四边形是菱形).
解:
本题考查了菱形的定义,菱形的定义也可
以作为菱形的判定方法.
新知小结
1
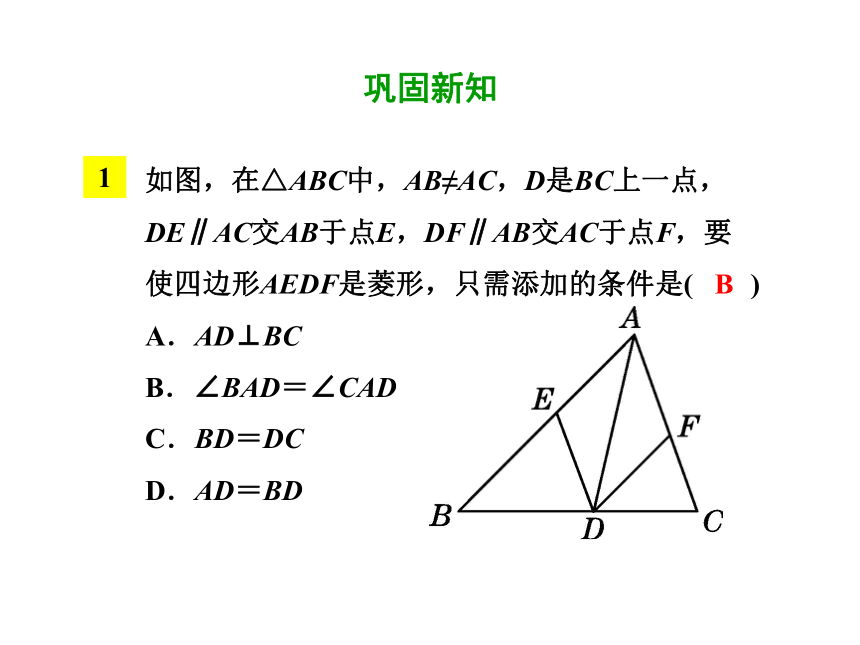
如图,在△ABC中,AB≠AC,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F,要使四边形AEDF是菱形,只需添加的条件是( )
A.AD⊥BC
B.∠BAD=∠CAD
C.BD=DC
D.AD=BD
B
巩固新知
2
知识点
菱形的边的性质
菱形具有平行四边形的所有性质.此外,菱形
还具有哪些特殊性质呢? 根据菱形的轴对称性,你
发现菱形的四条边具有什么大小关系?
问 题
菱形的四条边都相等.
合作探究
例2 如图所示,菱形ABCD中,∠B=60°,AB=2,
E、F分别是BC、CD的中点,连接AE、EF、
AF,则△AEF的周长为( )
A. B.
C. D.3
在菱形ABCD中,因为∠B=60°,连接AC,则
△ABC是等边三角形,又因为E分别是BC的中点,
所以AE垂直于BC,因此AE= ,所以
△AEF的周长为 ,故选B.
B
分析:
在菱形中作辅助线经常连接对角线,构造
三角形来做题,能够迎刃而解.
新知小结
1
边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm
C.12 cm D.15 cm
C
巩固新知
2
【中考·兰州】如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )
A.4
B.3
C.2
D.
B
3
【中考·重庆】如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
A.18 -9π
B.18-3π
C.9 -
D.18 -3π
A
4
【中考·鄂州】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′. 当CA′的长度最小时,CQ的长为( )
A.5
B.7
C.8
D.
B
3
知识点
菱形的对角线的性质
因为菱形是平行四边形,所以它具有平行四边形的
所有性质.由于它的一组邻边相等,它是否具有一般平行
四边形不具有的一些特殊性质呢?
思考
菱形的两条对角线AC与BD之间具有什么位置关系?
合作探究
对于菱形,我们仍然从它的对角线等方面进行研
究.可以发现并证明(请你自己完成证明),菱形还有以
下性质:
菱形的两条对角线互相垂直,并且每一条对角线
平分一组对角.
问 题
菱形的面积如何计算呢?
菱形的面积有两种计算方法:
一种是底乘以高的积;
另一种是对角线乘积的一半.所以在求菱形的面积
时,要灵活运用使计算简单.
由于菱形的四条边都相等,
所以要求其周长就要先求
出其边长.由菱形的性质
可知,其对角线互相垂直平分,因此可以在直角
三角形中利用勾股定理来进行计算.
例3 如图,在菱形ABCD中,对角线AC与BD相交于
点O,BD=12 cm,AC=6 cm.求菱形的周长.
导引:
∵四边形ABCD是菱形,
∴AC⊥BD,AO= AC,BO= BD.
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
在Rt△ABO中,由勾股定理,
得AB=
∴菱形的周长=4AB
解:
菱形的对角线将菱形分成四个全等的直角三角
形,我们通常将菱形问题中求相关线段的长转化为
求直角三角形中相关线段的长,再利用勾股定理来
计算.
新知小结
如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小
路AC和BD. 求两条小路的长(结果保留小数点后
两位)和花坛的面积(结果保留小数点后一位).
例4
∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO = ∠ABC = × 60°= 30°.
在Rt△OAB中,AO = AB = ×20=10,
∴花坛的两条小路长AC = 2AO =20 (m),
BD = 2BO=20 ≈34. 64 (m).
花坛的面积S四边形ABCD=4×S△OAB
= AC·BD=200 ≈346. 4 (m2).
解:
菱形的面积有三种计算方法:
(1)将其看成平行四边形,用底与高的积来求;
(2)对角线分得的四个全等直角三角形面积之和;
(3)两条对角线乘积的一半.
说明:读者可利用(1)(2)两种方法试一试;注意应
用(3)这种方法时不要忽视“一半”.
新知小结
1
四边形ABCD是菱形,对角线AC,BD相交于
点O,且AB = 5,AO = 4. 求AC和BD的长.
如图所示,因为四边形ABCD是菱形,
所以AC⊥BD,且AO=CO,OB=OD.
又因为AB=5,AO=4,
所以在Rt△AOB中,OB=
所以BD=2OB=2×3=6,AC=2AO=2×4=8.
解:
巩固新知
2
已知菱形的两条对角线的长分别是6和8,求菱形的周长和面积.
如图,由已知得,在菱形ABCD中,AC=8,BD=6.所以OA=OC=4,OB=OD=3.又由题意知AC⊥BD,所以在Rt△OAB中,AB=
又因为AB=BC=CD=AD,所以菱形的周长为AB+BC+CD+AD=4AB=4×5=20,
菱形的面积为 AC·BD= ×8×6=24.
解:
3
【 中考·南充】已知菱形的周长为4 ,两条对角线的和为6,则菱形的面积为( )
A.2 B.
C.3 D.4
D
4
【 中考·河北】求证:菱形的两条对角线互相垂直.
已知:如图,四边形ABCD是菱形,对
角线AC,BD交于点O. 求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;④∴AB=AD.
证明步骤正确的顺序是( )
A.③→②→①→④ B.③→④→①→②
C.①→②→④→③ D.①→④→③→②
B
5
【中考·长沙】如图,菱形ABCD的对角线AC,BD的长分别为6 cm,8 cm,则这个菱形的周长为( )
A.5 cm
B.10 cm
C.14 cm
D.20 cm
D
我们已经知道菱形是特殊的平行四边形,因此菱形是中心对称图形,想一想 菱形是不是轴对称图形?如果是轴对称图形,对称轴各几条?
菱形是轴对称图形,对称轴有两条.
拓展延伸
菱形是轴对称图形,它有两条对称轴. 对
称轴是分别经过两组对角顶点的两条直线.
例5 如图①,在菱形ABCD中,E,F分
别是CB,CD上的点,且BE=DF.
(1)求证:AE=AF.
(2)若∠B=60°,点E,F分
别是BC,CD的中点,求证:△AEF为等边三角形.
(1)要证AE=AF,只需证△AEB≌△AFD,由BE=
DF及菱形的相关性质进行证明即可.(2)如图②,要
证△AEF为等边三角形,由AE=AF知,只需证∠EAF
=60°即可,要证∠EAF=60°,只需证∠1=∠2=
30°即可,这可由菱形及等边三角形相关知识证出.
导引:
(1)∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
又∵BE=DF,
∴△ABE≌△ADF,∴AE=AF.
(2)如图②,连接AC.
∵四边形ABCD是菱形,∴AB=BC.
又∵∠B=60°,∴△ABC为等边三角形.
∴∠BAC=60°.
∵E为BC的中点,∴∠1= ∠BAC=30°.
同理∠2=30°,∴∠EAF=60°.
又∵AE=AF,∴△AEF为等边三角形.
证明:
菱形的每条对角线把菱形分成两个全等的等腰三
角形(特殊时为两个全等的等边三角形),两条对角线
把菱形分成四个全等的直角三角形.所以有关菱形的
一些证明与计算问题常常与特殊的三角形的有关问题
综合在一起.
新知小结
1
菱形是轴对称图形,其对称轴的条数为( )
A.2条 B.4条
C.6条 D.8条
A
巩固新知
2
【中考·益阳】下列性质中菱形不一定具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.既是轴对称图形又是中心对称图形
C
1.菱形的定义:有一组邻边相等的平行四边形叫做
菱形
2.菱形的性质:
(1)它具有平行四边形的一切性质.
(2)菱形的四条边相等.
(3)菱形的对角线互相垂直, 并且一条对角线平分
一组对角.
归纳新知
邻边
邻边相等
课后练习
B
B
四条边
12 cm
C
C
C
互相平分且垂直
平分一组对角
一半
对称轴
B
C
C
【答案】B
再 见
18.2.3 菱形及其性质
人教版数学八年级下册
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
温故知新
复习旧知
同学们,将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形呢?
菱形及其性质
导入新知
学习目标
1.掌握的定义和性质及菱形面积的求法.
2.灵活运用菱形的性质解决问题.
1
知识点
菱形的定义
在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
平行四边形
有一组邻边相等的平行四边形
菱形
邻边相等
合作探究
有一组 的 叫做
邻边相等
平行四边形
A
D
C
B
∵四边形ABCD是平
行四边形
AB=BC
∴四边形ABCD是菱形
菱形.
感受生活
你能举出生活中你看到的菱形吗?
生活
感受
例1 已知:如图,在△ABC中,CD平分∠ACB交AB
于点D,DE∥AC交BC于点E,DF∥BC交AC于
点F. 四边形DECF是菱形吗?为什么?
因为DE∥FC,DF∥EC,所
以四边形DECF为平行四边
形,再根据有一组邻边相等
的平行四边形是菱形求证即
可.
导引:
四边形DECF是菱形.理由如下:
∵DE∥FC,DF∥EC,
∴四边形DECF为平行四边形.
由AC∥DE,知∠2=∠3.
∵CD平分∠ACB,
∴∠1=∠2,∴∠1=∠3,∴DE=EC,
∴平行四边形DECF为菱形(有一组邻边相等的平
行四边形是菱形).
解:
本题考查了菱形的定义,菱形的定义也可
以作为菱形的判定方法.
新知小结
1
如图,在△ABC中,AB≠AC,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F,要使四边形AEDF是菱形,只需添加的条件是( )
A.AD⊥BC
B.∠BAD=∠CAD
C.BD=DC
D.AD=BD
B
巩固新知
2
知识点
菱形的边的性质
菱形具有平行四边形的所有性质.此外,菱形
还具有哪些特殊性质呢? 根据菱形的轴对称性,你
发现菱形的四条边具有什么大小关系?
问 题
菱形的四条边都相等.
合作探究
例2 如图所示,菱形ABCD中,∠B=60°,AB=2,
E、F分别是BC、CD的中点,连接AE、EF、
AF,则△AEF的周长为( )
A. B.
C. D.3
在菱形ABCD中,因为∠B=60°,连接AC,则
△ABC是等边三角形,又因为E分别是BC的中点,
所以AE垂直于BC,因此AE= ,所以
△AEF的周长为 ,故选B.
B
分析:
在菱形中作辅助线经常连接对角线,构造
三角形来做题,能够迎刃而解.
新知小结
1
边长为3 cm的菱形的周长是( )
A.6 cm B.9 cm
C.12 cm D.15 cm
C
巩固新知
2
【中考·兰州】如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是( )
A.4
B.3
C.2
D.
B
3
【中考·重庆】如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
A.18 -9π
B.18-3π
C.9 -
D.18 -3π
A
4
【中考·鄂州】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′. 当CA′的长度最小时,CQ的长为( )
A.5
B.7
C.8
D.
B
3
知识点
菱形的对角线的性质
因为菱形是平行四边形,所以它具有平行四边形的
所有性质.由于它的一组邻边相等,它是否具有一般平行
四边形不具有的一些特殊性质呢?
思考
菱形的两条对角线AC与BD之间具有什么位置关系?
合作探究
对于菱形,我们仍然从它的对角线等方面进行研
究.可以发现并证明(请你自己完成证明),菱形还有以
下性质:
菱形的两条对角线互相垂直,并且每一条对角线
平分一组对角.
问 题
菱形的面积如何计算呢?
菱形的面积有两种计算方法:
一种是底乘以高的积;
另一种是对角线乘积的一半.所以在求菱形的面积
时,要灵活运用使计算简单.
由于菱形的四条边都相等,
所以要求其周长就要先求
出其边长.由菱形的性质
可知,其对角线互相垂直平分,因此可以在直角
三角形中利用勾股定理来进行计算.
例3 如图,在菱形ABCD中,对角线AC与BD相交于
点O,BD=12 cm,AC=6 cm.求菱形的周长.
导引:
∵四边形ABCD是菱形,
∴AC⊥BD,AO= AC,BO= BD.
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
在Rt△ABO中,由勾股定理,
得AB=
∴菱形的周长=4AB
解:
菱形的对角线将菱形分成四个全等的直角三角
形,我们通常将菱形问题中求相关线段的长转化为
求直角三角形中相关线段的长,再利用勾股定理来
计算.
新知小结
如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小
路AC和BD. 求两条小路的长(结果保留小数点后
两位)和花坛的面积(结果保留小数点后一位).
例4
∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO = ∠ABC = × 60°= 30°.
在Rt△OAB中,AO = AB = ×20=10,
∴花坛的两条小路长AC = 2AO =20 (m),
BD = 2BO=20 ≈34. 64 (m).
花坛的面积S四边形ABCD=4×S△OAB
= AC·BD=200 ≈346. 4 (m2).
解:
菱形的面积有三种计算方法:
(1)将其看成平行四边形,用底与高的积来求;
(2)对角线分得的四个全等直角三角形面积之和;
(3)两条对角线乘积的一半.
说明:读者可利用(1)(2)两种方法试一试;注意应
用(3)这种方法时不要忽视“一半”.
新知小结
1
四边形ABCD是菱形,对角线AC,BD相交于
点O,且AB = 5,AO = 4. 求AC和BD的长.
如图所示,因为四边形ABCD是菱形,
所以AC⊥BD,且AO=CO,OB=OD.
又因为AB=5,AO=4,
所以在Rt△AOB中,OB=
所以BD=2OB=2×3=6,AC=2AO=2×4=8.
解:
巩固新知
2
已知菱形的两条对角线的长分别是6和8,求菱形的周长和面积.
如图,由已知得,在菱形ABCD中,AC=8,BD=6.所以OA=OC=4,OB=OD=3.又由题意知AC⊥BD,所以在Rt△OAB中,AB=
又因为AB=BC=CD=AD,所以菱形的周长为AB+BC+CD+AD=4AB=4×5=20,
菱形的面积为 AC·BD= ×8×6=24.
解:
3
【 中考·南充】已知菱形的周长为4 ,两条对角线的和为6,则菱形的面积为( )
A.2 B.
C.3 D.4
D
4
【 中考·河北】求证:菱形的两条对角线互相垂直.
已知:如图,四边形ABCD是菱形,对
角线AC,BD交于点O. 求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;④∴AB=AD.
证明步骤正确的顺序是( )
A.③→②→①→④ B.③→④→①→②
C.①→②→④→③ D.①→④→③→②
B
5
【中考·长沙】如图,菱形ABCD的对角线AC,BD的长分别为6 cm,8 cm,则这个菱形的周长为( )
A.5 cm
B.10 cm
C.14 cm
D.20 cm
D
我们已经知道菱形是特殊的平行四边形,因此菱形是中心对称图形,想一想 菱形是不是轴对称图形?如果是轴对称图形,对称轴各几条?
菱形是轴对称图形,对称轴有两条.
拓展延伸
菱形是轴对称图形,它有两条对称轴. 对
称轴是分别经过两组对角顶点的两条直线.
例5 如图①,在菱形ABCD中,E,F分
别是CB,CD上的点,且BE=DF.
(1)求证:AE=AF.
(2)若∠B=60°,点E,F分
别是BC,CD的中点,求证:△AEF为等边三角形.
(1)要证AE=AF,只需证△AEB≌△AFD,由BE=
DF及菱形的相关性质进行证明即可.(2)如图②,要
证△AEF为等边三角形,由AE=AF知,只需证∠EAF
=60°即可,要证∠EAF=60°,只需证∠1=∠2=
30°即可,这可由菱形及等边三角形相关知识证出.
导引:
(1)∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
又∵BE=DF,
∴△ABE≌△ADF,∴AE=AF.
(2)如图②,连接AC.
∵四边形ABCD是菱形,∴AB=BC.
又∵∠B=60°,∴△ABC为等边三角形.
∴∠BAC=60°.
∵E为BC的中点,∴∠1= ∠BAC=30°.
同理∠2=30°,∴∠EAF=60°.
又∵AE=AF,∴△AEF为等边三角形.
证明:
菱形的每条对角线把菱形分成两个全等的等腰三
角形(特殊时为两个全等的等边三角形),两条对角线
把菱形分成四个全等的直角三角形.所以有关菱形的
一些证明与计算问题常常与特殊的三角形的有关问题
综合在一起.
新知小结
1
菱形是轴对称图形,其对称轴的条数为( )
A.2条 B.4条
C.6条 D.8条
A
巩固新知
2
【中考·益阳】下列性质中菱形不一定具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.既是轴对称图形又是中心对称图形
C
1.菱形的定义:有一组邻边相等的平行四边形叫做
菱形
2.菱形的性质:
(1)它具有平行四边形的一切性质.
(2)菱形的四条边相等.
(3)菱形的对角线互相垂直, 并且一条对角线平分
一组对角.
归纳新知
邻边
邻边相等
课后练习
B
B
四条边
12 cm
C
C
C
互相平分且垂直
平分一组对角
一半
对称轴
B
C
C
【答案】B
再 见
