2020-2021学年人教版八年级下册数学:18.1.1平行四边形的性质 (2)(24张)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学:18.1.1平行四边形的性质 (2)(24张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
学习目标
1、什么叫做平行四边形?
2、在对平行四边形认识的基础上,探索并掌握平行四边形的性质。
3、平行四边形有哪些性质?
4、能够利用平行四边形的性质去解决日常生活中的数学问题.
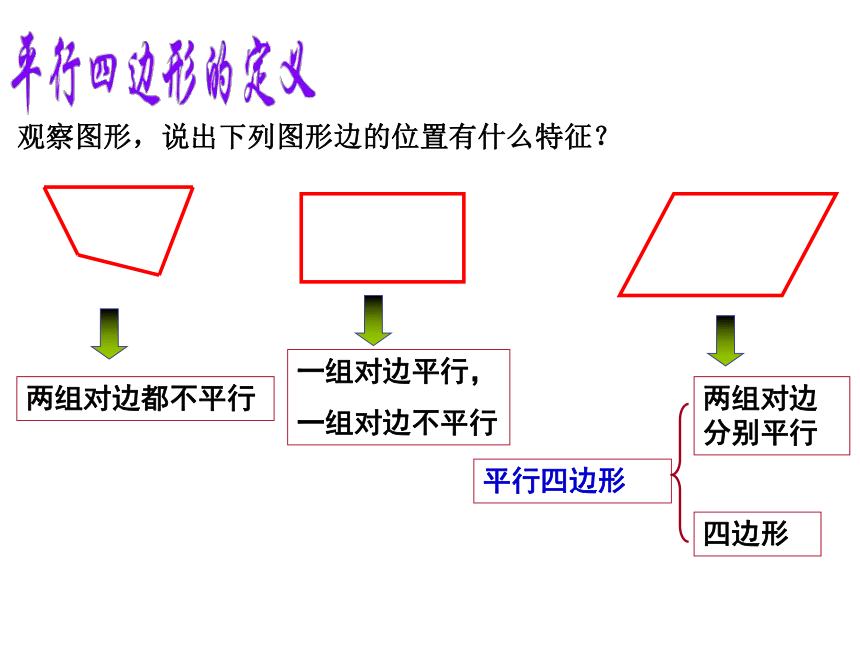
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
观察图形,说出下列图形边的位置有什么特征?
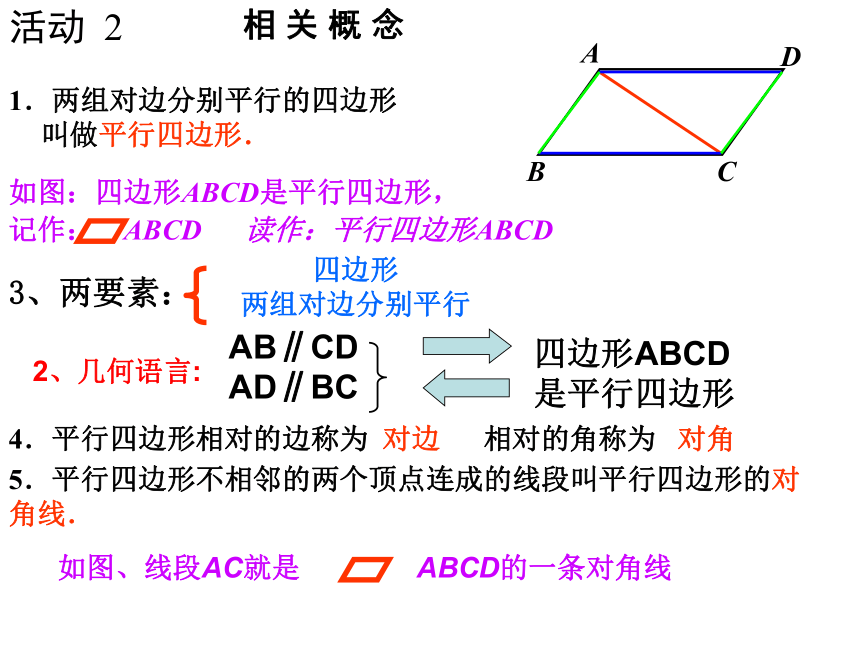
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形,
记作:
ABCD
读作:平行四边形ABCD
5.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
4.平行四边形相对的边称为
对边
相对的角称为
对角
相
关
概
念
A
D
C
B
活动
2
2、几何语言:
AB∥CD
AD∥BC
四边形ABCD是平行四边形
如图、线段AC就是
ABCD的一条对角线
3、两要素:
四边形
两组对边分别平行
A
B
C
D
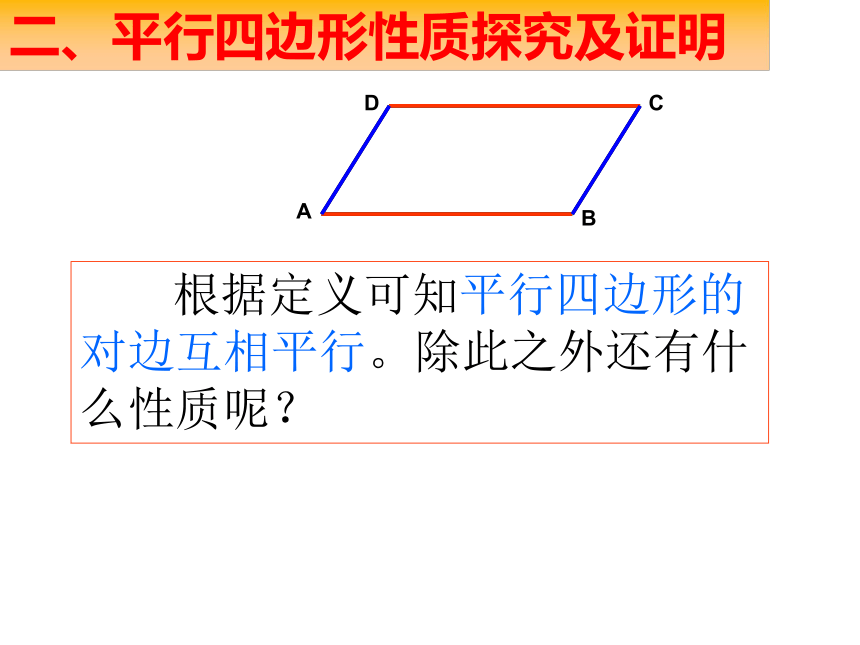
根据定义可知平行四边形的对边互相平行。除此之外还有什么性质呢?
二、平行四边形性质探究及证明
画一画
请同桌合作用定义的方法在网格纸上画一个平行四边形ABCD,四个顶点都在网格顶点上。
A
B
C
D
同桌两个同学合作,用直尺,量角器等工具度量你刚才画的平行四边形的边和角,并记录下数据,猜想平行四边形的对边对角之间的关系?
量一量
动态展示
猜一猜:平行四边形对边、对角有怎样的数量关系?
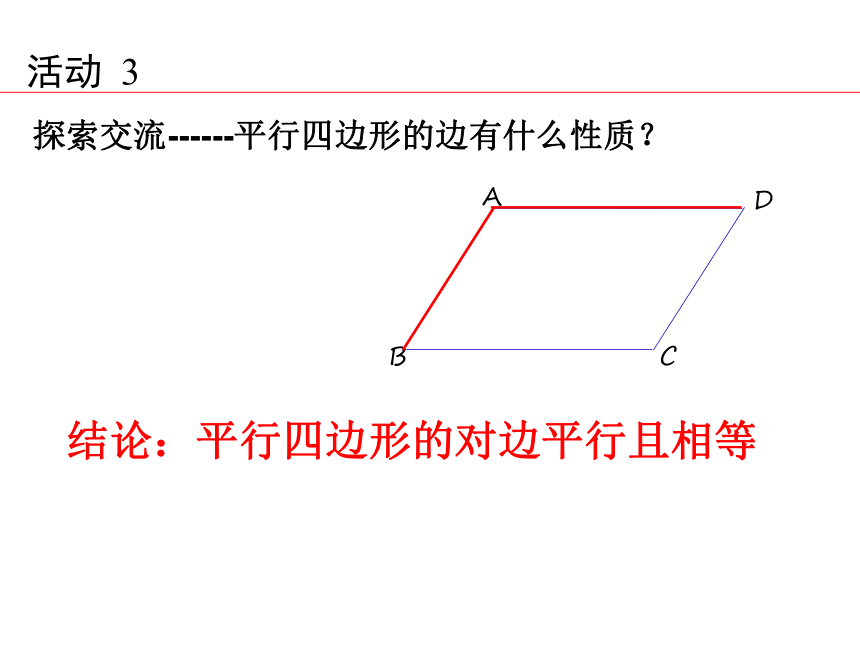
探索交流------平行四边形的边有什么性质?
C
B
A
D
结论:平行四边形的对边平行且相等
活动
3
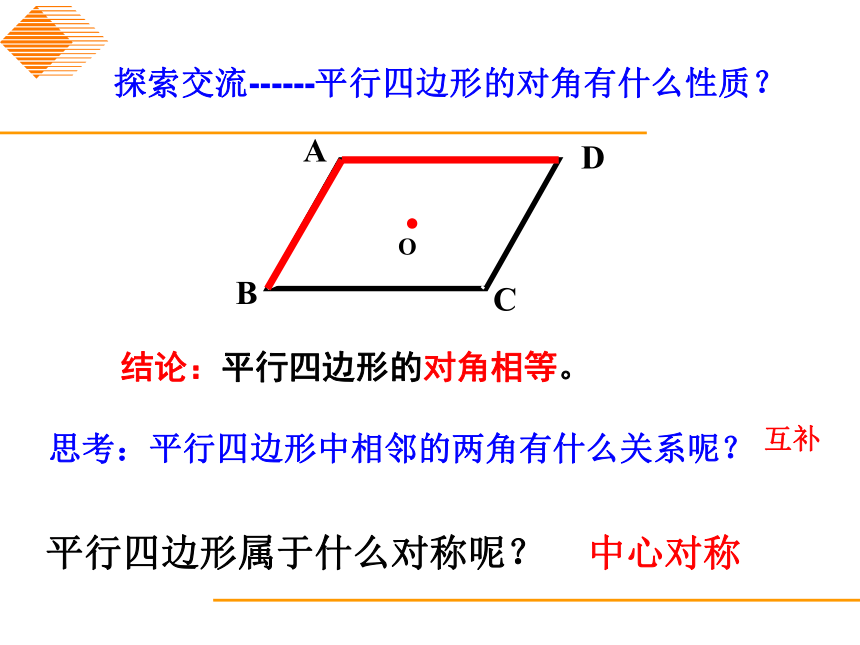
探索交流------平行四边形的对角有什么性质?
A
B
C
D
O
结论:平行四边形的对角相等。
思考:平行四边形中相邻的两角有什么关系呢?
平行四边形属于什么对称呢?
中心对称
互补
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的邻角互补.
平行四边形的性质
A
B
C
D
总结归纳:
平行四边形是中心对称对称图形.
几何语言描述:
∵
四边形ABCD是平行四边形
∴
∠D=
∠B,∠C=
∠A
(平行四边形的对角相等)
∠A+∠B=180°∠A+∠D=180?,∠B+∠C=180?,
∠C+∠D=180?
∵
四边形ABCD是平行四边形
∴
AB=CD,AD=BC.(平行四边形的对边相等)
已知:
ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连结AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,AC=CA,∠3=∠4
∴
ABC≌
CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在
ABC和
CDA中
A
B
C
D
1
2
3
4
性质证明
1.已知:
ABCD中,∠A=100°,你能求出其他各角的度数吗?说说你的理由.
A
D
C
B
活动
4
学
以
致
用
变题1、
中,∠A比∠B大
30
?,
则
∠A=__,∠D=__.
ABCD
变题2、
中,如果∠A的外角是
50°,那么平行四边形的每个内角是多少度?
ABCD
2、如图,已知
中,AB=8,BC=4,其余各边长为多少?其周长等于多少?
ABCD
A
B
C
D
变题2、若
的周长是30㎝,AB
:CB=3
:2,
则AD=
㎝,CD=
㎝.
ABCD
变题1、
的周长是20,已知AB=6,则BC=__,CD=__.
ABCD
解:∵
四边形ABCD是平行四边形
∴AB=CD,
AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴
AD=BC=10m
A
B
C
D
例1
如图
,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
运用所学知识解决问题
有一块形状如图
所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
例2
已知:如图,
AD∥BC,AE∥CD,BD平分∠ABC
,求证:AB=CE.
运用所学知识解决问题
A
D
B
E
C
1
2
3
求
:
的面积.
已知
:
如图,
,
AB=8cm,BC=10cm,∠B=30°.
ABCD
A
B
C
D
解:
过A作AE⊥BC于点E
∠B=
30°,
AB=8
.
ABCD
E
在Rt△ABE中,
ABCE的面积
∴
∴
AE=
AB=
×8
=4
2
1
2
1
S
ABCD
=BC·AE
=10×4
=40(cm2).
例2(补充)如图,在平行四边形ABCD中,AE=CF,
求证:AF=CE
2.如图4.3-9,在ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足.
求证:BE=DF
用两个三边不等的完全相同的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
你能以三角形为基础画平行四边形吗?
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
课堂回顾
1、定义:两组对边分别平行的四边形叫做平行四边形.
2、性质:平行四边形的对边平行且相等。
平行四边形的对角相等。
平行四边形的邻角互补。
3、性质的运用
选做题
1、平行四边形一个角的平分线分对边为5和4两部分,求这个平行四边形的周长。
2、如图,在
ABCD中,点E,F在对角线AC上,且AE=CF.请你以点F为一个端点,和图中已标明字母的某一点连成一条线段,猜想并证明它和图中已有的某一线段相等(只需证明一组线段相等即可).
(1)连结_________
(2)猜想:________=_________.
(3)证明:
学习目标
1、什么叫做平行四边形?
2、在对平行四边形认识的基础上,探索并掌握平行四边形的性质。
3、平行四边形有哪些性质?
4、能够利用平行四边形的性质去解决日常生活中的数学问题.
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
观察图形,说出下列图形边的位置有什么特征?
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形,
记作:
ABCD
读作:平行四边形ABCD
5.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
4.平行四边形相对的边称为
对边
相对的角称为
对角
相
关
概
念
A
D
C
B
活动
2
2、几何语言:
AB∥CD
AD∥BC
四边形ABCD是平行四边形
如图、线段AC就是
ABCD的一条对角线
3、两要素:
四边形
两组对边分别平行
A
B
C
D
根据定义可知平行四边形的对边互相平行。除此之外还有什么性质呢?
二、平行四边形性质探究及证明
画一画
请同桌合作用定义的方法在网格纸上画一个平行四边形ABCD,四个顶点都在网格顶点上。
A
B
C
D
同桌两个同学合作,用直尺,量角器等工具度量你刚才画的平行四边形的边和角,并记录下数据,猜想平行四边形的对边对角之间的关系?
量一量
动态展示
猜一猜:平行四边形对边、对角有怎样的数量关系?
探索交流------平行四边形的边有什么性质?
C
B
A
D
结论:平行四边形的对边平行且相等
活动
3
探索交流------平行四边形的对角有什么性质?
A
B
C
D
O
结论:平行四边形的对角相等。
思考:平行四边形中相邻的两角有什么关系呢?
平行四边形属于什么对称呢?
中心对称
互补
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的邻角互补.
平行四边形的性质
A
B
C
D
总结归纳:
平行四边形是中心对称对称图形.
几何语言描述:
∵
四边形ABCD是平行四边形
∴
∠D=
∠B,∠C=
∠A
(平行四边形的对角相等)
∠A+∠B=180°∠A+∠D=180?,∠B+∠C=180?,
∠C+∠D=180?
∵
四边形ABCD是平行四边形
∴
AB=CD,AD=BC.(平行四边形的对边相等)
已知:
ABCD(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连结AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
∠1=∠2,AC=CA,∠3=∠4
∴
ABC≌
CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在
ABC和
CDA中
A
B
C
D
1
2
3
4
性质证明
1.已知:
ABCD中,∠A=100°,你能求出其他各角的度数吗?说说你的理由.
A
D
C
B
活动
4
学
以
致
用
变题1、
中,∠A比∠B大
30
?,
则
∠A=__,∠D=__.
ABCD
变题2、
中,如果∠A的外角是
50°,那么平行四边形的每个内角是多少度?
ABCD
2、如图,已知
中,AB=8,BC=4,其余各边长为多少?其周长等于多少?
ABCD
A
B
C
D
变题2、若
的周长是30㎝,AB
:CB=3
:2,
则AD=
㎝,CD=
㎝.
ABCD
变题1、
的周长是20,已知AB=6,则BC=__,CD=__.
ABCD
解:∵
四边形ABCD是平行四边形
∴AB=CD,
AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴
AD=BC=10m
A
B
C
D
例1
如图
,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
运用所学知识解决问题
有一块形状如图
所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm、BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
例2
已知:如图,
AD∥BC,AE∥CD,BD平分∠ABC
,求证:AB=CE.
运用所学知识解决问题
A
D
B
E
C
1
2
3
求
:
的面积.
已知
:
如图,
,
AB=8cm,BC=10cm,∠B=30°.
ABCD
A
B
C
D
解:
过A作AE⊥BC于点E
∠B=
30°,
AB=8
.
ABCD
E
在Rt△ABE中,
ABCE的面积
∴
∴
AE=
AB=
×8
=4
2
1
2
1
S
ABCD
=BC·AE
=10×4
=40(cm2).
例2(补充)如图,在平行四边形ABCD中,AE=CF,
求证:AF=CE
2.如图4.3-9,在ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足.
求证:BE=DF
用两个三边不等的完全相同的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
你能以三角形为基础画平行四边形吗?
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
课堂回顾
1、定义:两组对边分别平行的四边形叫做平行四边形.
2、性质:平行四边形的对边平行且相等。
平行四边形的对角相等。
平行四边形的邻角互补。
3、性质的运用
选做题
1、平行四边形一个角的平分线分对边为5和4两部分,求这个平行四边形的周长。
2、如图,在
ABCD中,点E,F在对角线AC上,且AE=CF.请你以点F为一个端点,和图中已标明字母的某一点连成一条线段,猜想并证明它和图中已有的某一线段相等(只需证明一组线段相等即可).
(1)连结_________
(2)猜想:________=_________.
(3)证明:
