2020-2021学年北师大版八年级数学下册课件:4.1因式分解(18张)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册课件:4.1因式分解(18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 16:28:42 | ||
图片预览






文档简介
北师大版数学八年级(下)
1.因式分解
第四章
因式分解
教学目标
1.由因数分解类比因数分解,理解因式分解的概念.(重点)
重点难点
2.弄清因式分解与整式乘法的关系,会分辨因式分解与整式乘法.(难点)
教学过程
温故知新
2.单项式乘以多项式法则与多项式乘以多项式的法则?
单项式乘以多项式:a(b+c)=ab+ac
多项式乘以多项式:(a+b)(m+n)=am+an+bm+bn
1.什么是整式?
单项式与多项式统称为整式.
教学过程
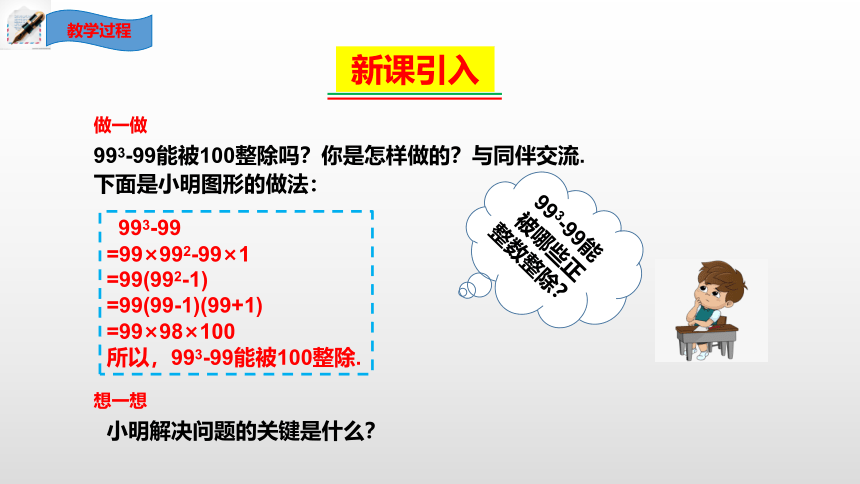
新课引入
做一做
993-99能被100整除吗?你是怎样做的?与同伴交流.
下面是小明图形的做法:
993-99
=99×992-99×1
=99(992-1)
=99(99-1)(99+1)
=99×98×100
所以,993-99能被100整除.
想一想
993-99能被哪些正整数整除?
小明解决问题的关键是什么?
教学过程
新课引入
上面问题中小明解决问题的关键是把一个数式化成了几个数的积的形式.
本节课我们要研究的是把一个多项式式化成几个整式的积的形式——因式分解.
教学过程
新知探究
做一做
上面把993-99化成了几个数的积的形式.你能把a3-a化成几个整式的积的形式吗?
a3-a
=a×a2-a×1
=a(a2-1)
=a(a-1)(a+1).
用到了我们学过的哪些知识?
教学过程
新知探究
试一试
你能把下面的几个多项式化成几个整式的积的形式吗?
5a2-5a=( )( )
ax+ay-a=( )( )
m2-25=( )( )
y2+4y+4=( )( )
5a
a-1
a
x+y-1
m+5
m-5
y+2
y+2
比较上面这几个等式你发现了什么?
等式的左边都是多项式,等式的右边都是几个整式的积的形式.
教学过程
新知探究
做一做
观察下面拼图过程,写出相应等式.
c
a
m
m
m
b
m
a+b+c
=
ma+mb+mc
m(a+b+c)
我们用了什么方法写出了上面这个等式?你能同样的方法写出课本中第二个等式吗?
教学过程
新知探究
议一议
5a2-5a=5a(a-1)
ax+ay-a=a( x+y-1)
m2-25=(m+5)(m-5)
y2+4y+4=(y+2)2=(y+2)(y+2)
ma+mb+mc=m(a+b+c)
x2+2x+1=(x+1)2
左面是我们用不同的方法写出的等式,你能说出这些变形的共同特点吗?
共同特点:等式左边是一个多项式,等式右边是几个等式的积的形式。
教学过程
新知归纳
像上面那样,我们可以把一个多项式进行变形,使它们变成几个整式相乘的积的形式. 像这样的变形我们叫做因式分解.
定义:把一个多项式变成几个整式相乘的积的形式,这种变形叫做因式分解.
像a3-a=a(a+1)(a-1),ma+mb+mc=m(a+b+c),x2+2x+1=(x+1)2都是因式分解.因式分解也可以称为分解因式.
注意:把一个多项式进行因式分解后的每一个整式都是原多项式的因式.
教学过程
现学现用
判断下面的变形是否是因式分解?
做一做
a2-3a=a(a-3) ( )
x2-y2+1=(x+y)(x-y)+1 ( )
x2+2x-3=(x+3)(x-1) ( )
(m+1)(m-1)=m2-1 ( )
12x3y2=6x2y·2xy ( )
x2+1=x( x+ ) ( )
是
否
是
否
否
否
教学过程
新知探究
整式乘法与因式分解的关系
做一做
完成课本第91页的“做一做”.
完成“做一做”,你能说出整式乘法与因式分解的关系吗?
教学过程
新知探究
整式乘法与因式分解的关系
想一想
由3x(x-1)到3x2-3x的变形是什么运算?
由3x2-3x到3x(x-1)的变形呢?
由3x(x-1)到3x2-3x的变形是整式乘法.
由3x2-3x到3x(x-1)的变形是因式分解.
整式乘法与因式分解是两个互逆的过程.
3x2-3x
3x(x-1)
因式分解
整式乘法
教学过程
典例精析
例. 若2(x-m)(x+2)是多项式2x2+nx-6+n分解后的结果,求m+n的平方根.
解:2(x-m)(x+2)=2x2+(4-2m)x-4m,
因为2(x-m)(x+2)是多项式2x2+nx-6+n分解后的结果,
所以2x2+(4-2m)x-4m=2x2+nx-6+n.
4-2m=n
-4m=-6+n
{
所以
解得 m=1
n=2
{
所以m+n=2+1=3.
所以m+n的平方根是± .
教学过程
学以致用
已知二次三项式x2-4x+m有一个因式是(x+3),求另一个因式以及的m值.
提示:可以设另一个因式为(x+n),根据因式分解的概念可解.
教学过程
课堂小结
今天你学到了什么?
定义:把一个多项式变成几个整式相乘的积的形式,这种变形叫做因式分解.
1.因式分解的概念:
2.因式分解与整式乘法的关系:
因式分解与整式乘法是互逆的关系.
课后巩固
分层作业
第一层:课本第94页习题第1、3题
第二层:课本第94页习题第3、4、5题.
结束新课
1.因式分解
第四章
因式分解
教学目标
1.由因数分解类比因数分解,理解因式分解的概念.(重点)
重点难点
2.弄清因式分解与整式乘法的关系,会分辨因式分解与整式乘法.(难点)
教学过程
温故知新
2.单项式乘以多项式法则与多项式乘以多项式的法则?
单项式乘以多项式:a(b+c)=ab+ac
多项式乘以多项式:(a+b)(m+n)=am+an+bm+bn
1.什么是整式?
单项式与多项式统称为整式.
教学过程
新课引入
做一做
993-99能被100整除吗?你是怎样做的?与同伴交流.
下面是小明图形的做法:
993-99
=99×992-99×1
=99(992-1)
=99(99-1)(99+1)
=99×98×100
所以,993-99能被100整除.
想一想
993-99能被哪些正整数整除?
小明解决问题的关键是什么?
教学过程
新课引入
上面问题中小明解决问题的关键是把一个数式化成了几个数的积的形式.
本节课我们要研究的是把一个多项式式化成几个整式的积的形式——因式分解.
教学过程
新知探究
做一做
上面把993-99化成了几个数的积的形式.你能把a3-a化成几个整式的积的形式吗?
a3-a
=a×a2-a×1
=a(a2-1)
=a(a-1)(a+1).
用到了我们学过的哪些知识?
教学过程
新知探究
试一试
你能把下面的几个多项式化成几个整式的积的形式吗?
5a2-5a=( )( )
ax+ay-a=( )( )
m2-25=( )( )
y2+4y+4=( )( )
5a
a-1
a
x+y-1
m+5
m-5
y+2
y+2
比较上面这几个等式你发现了什么?
等式的左边都是多项式,等式的右边都是几个整式的积的形式.
教学过程
新知探究
做一做
观察下面拼图过程,写出相应等式.
c
a
m
m
m
b
m
a+b+c
=
ma+mb+mc
m(a+b+c)
我们用了什么方法写出了上面这个等式?你能同样的方法写出课本中第二个等式吗?
教学过程
新知探究
议一议
5a2-5a=5a(a-1)
ax+ay-a=a( x+y-1)
m2-25=(m+5)(m-5)
y2+4y+4=(y+2)2=(y+2)(y+2)
ma+mb+mc=m(a+b+c)
x2+2x+1=(x+1)2
左面是我们用不同的方法写出的等式,你能说出这些变形的共同特点吗?
共同特点:等式左边是一个多项式,等式右边是几个等式的积的形式。
教学过程
新知归纳
像上面那样,我们可以把一个多项式进行变形,使它们变成几个整式相乘的积的形式. 像这样的变形我们叫做因式分解.
定义:把一个多项式变成几个整式相乘的积的形式,这种变形叫做因式分解.
像a3-a=a(a+1)(a-1),ma+mb+mc=m(a+b+c),x2+2x+1=(x+1)2都是因式分解.因式分解也可以称为分解因式.
注意:把一个多项式进行因式分解后的每一个整式都是原多项式的因式.
教学过程
现学现用
判断下面的变形是否是因式分解?
做一做
a2-3a=a(a-3) ( )
x2-y2+1=(x+y)(x-y)+1 ( )
x2+2x-3=(x+3)(x-1) ( )
(m+1)(m-1)=m2-1 ( )
12x3y2=6x2y·2xy ( )
x2+1=x( x+ ) ( )
是
否
是
否
否
否
教学过程
新知探究
整式乘法与因式分解的关系
做一做
完成课本第91页的“做一做”.
完成“做一做”,你能说出整式乘法与因式分解的关系吗?
教学过程
新知探究
整式乘法与因式分解的关系
想一想
由3x(x-1)到3x2-3x的变形是什么运算?
由3x2-3x到3x(x-1)的变形呢?
由3x(x-1)到3x2-3x的变形是整式乘法.
由3x2-3x到3x(x-1)的变形是因式分解.
整式乘法与因式分解是两个互逆的过程.
3x2-3x
3x(x-1)
因式分解
整式乘法
教学过程
典例精析
例. 若2(x-m)(x+2)是多项式2x2+nx-6+n分解后的结果,求m+n的平方根.
解:2(x-m)(x+2)=2x2+(4-2m)x-4m,
因为2(x-m)(x+2)是多项式2x2+nx-6+n分解后的结果,
所以2x2+(4-2m)x-4m=2x2+nx-6+n.
4-2m=n
-4m=-6+n
{
所以
解得 m=1
n=2
{
所以m+n=2+1=3.
所以m+n的平方根是± .
教学过程
学以致用
已知二次三项式x2-4x+m有一个因式是(x+3),求另一个因式以及的m值.
提示:可以设另一个因式为(x+n),根据因式分解的概念可解.
教学过程
课堂小结
今天你学到了什么?
定义:把一个多项式变成几个整式相乘的积的形式,这种变形叫做因式分解.
1.因式分解的概念:
2.因式分解与整式乘法的关系:
因式分解与整式乘法是互逆的关系.
课后巩固
分层作业
第一层:课本第94页习题第1、3题
第二层:课本第94页习题第3、4、5题.
结束新课
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
