2020-2021学年湘教版(2012)数学八年级下册 2.1.1 多边形 多边形的概念及内角和 课件(29张)
文档属性
| 名称 | 2020-2021学年湘教版(2012)数学八年级下册 2.1.1 多边形 多边形的概念及内角和 课件(29张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 840.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 16:31:27 | ||
图片预览






文档简介
由这图形你抽象出什么几何图形?
三角形
复习回顾
在同一平面内,由不在同一直线上的三条线段首尾顺次连接而成的图形叫作三角形.
三角形的定义:
三角形的边、顶点、内角的概念:
三角形的内角和定理:
三角形的内角和等于180°.
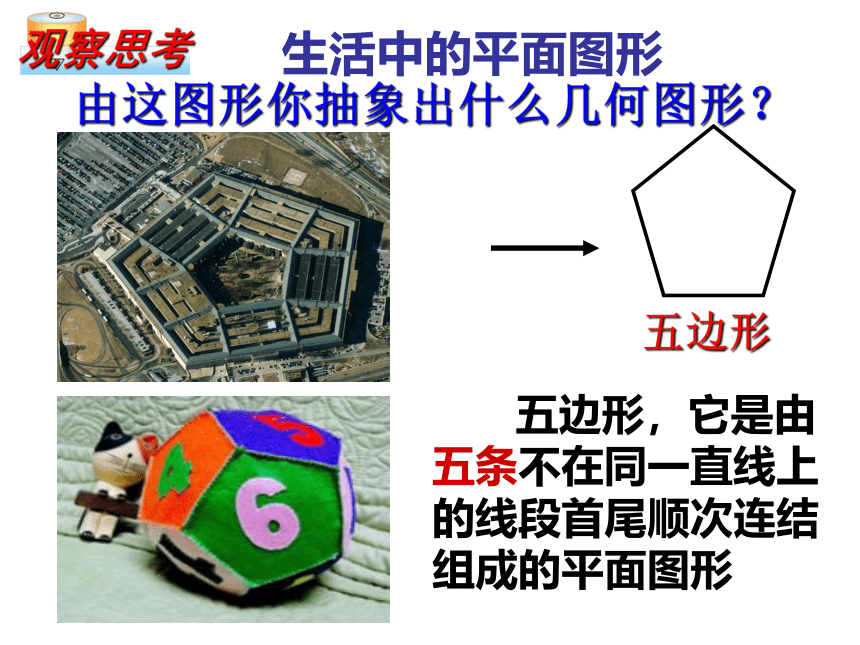
生活中的平面图形
四边形
由这图形你抽象出什么几何图形?
四边形是由不在同一直线上的四条线段首尾顺次连结组成的平面图形.
观察思考
生活中的平面图形
由这图形你抽象出什么几何图形?
五边形
五边形,它是由五条不在同一直线上的线段首尾顺次连结组成的平面图形
观察思考
生活中的平面图形
六边形
由这图形你抽象出什么几何图形?
六边形,它是由不在同一直线上的六条线段首尾顺次连结组成的平面图形.
观察思考
生活中的平面图形
由这图形你抽象出什么几何图形?
八边形
八边形,它是由不在同一直线上的八条线段首尾顺次连结组成的平面图形.
观察思考
生活中的平面图形
湘教版八年级《数学》下册
多边形的概念及内角和
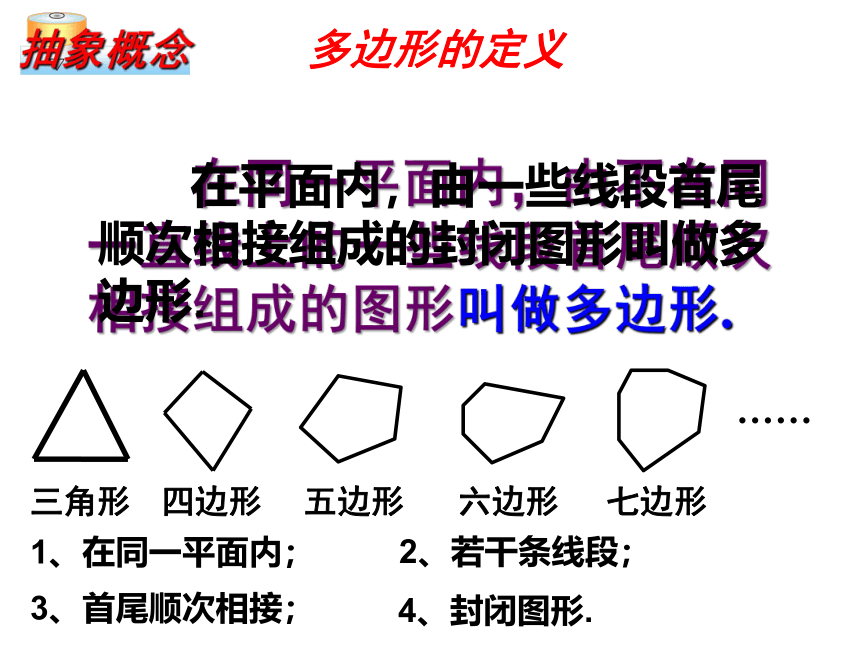
在同一平面内,由不在同一直线上的一些线段首尾顺次相接组成的图形叫做多边形.
多边形的定义
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
抽象概念
……
五边形
六边形
七边形
三角形
四边形
1、在同一平面内;
2、若干条线段;
3、首尾顺次相接;
4、封闭图形.
多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形.
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形.
多边形的定义
抽象概念
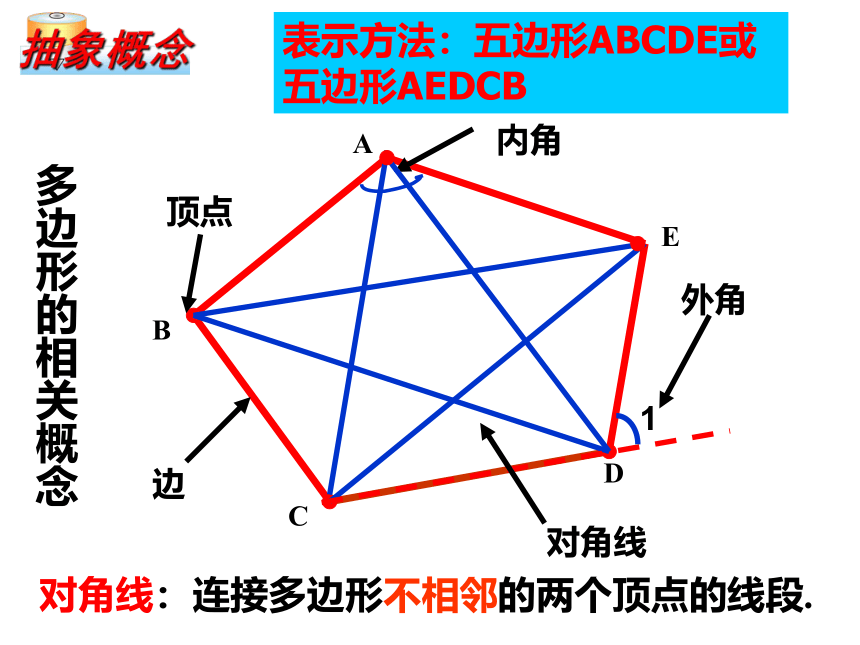
内角
对角线
对角线:连接多边形不相邻的两个顶点的线段.
表示方法:五边形ABCDE或五边形AEDCB
A
B
C
D
E
外角
1
多边形的相关概念
顶点
边
抽象概念
n边形有_____个顶点,
_____条边,
_____个内角,
_____个外角,
_____条对角线.
n
n
n
2n
归纳总结1
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
三角形
六边形
四边形
八边形
……..
五边形
请说出下列图形从某一顶点出发的对角线的条数:
多边形的对角线
合作探究
0
1
2
3
5
从同一顶点引出的对角线的条数:
1
2
3
n-3
分割出的三角形的个数:
2
3
4
n-2
0
1
n边形
……
三角形
四边形
五边形
六边形
n边形
……
四边形
合作探究
n边形从一个顶点出发的对角线条数为 条(n≥3);n边形被分成了 个三角形.
n边形共有对角线 条(n≥3)
(n-3)
?
归纳总结2
(n-2)
(1)
(2)
A
B
C
D
E
F
G
H
你能说出这两幅图形的异同点吗?
合作探究
多边形的分类
如图,画出四边形ABCD的任何一条边所在直线,整个四边形都在这条直线的同一侧,这样的四边形叫做凸四边形.
A
B
C
D
合作探究
A
B
D
C
四边形ABCD是凹四边形,因为画出边CD(或BC)所在直线,整个四边形不都在这条直线的同一侧.
凹四边形
多边形的分类
合作探究
正多边形的定义
正方形的各个角都相等,各条边都相等.像正方形这样,在平面内,各个角都相等,各条边都相等的多边形叫做正多边形.
例如:
正三角形
正方形
正五边形
正六边形
合作探究
当n≥3时,必须同时满足以下两个条件:
(1)是各边相等,
(2)是各角相等.
两者缺一不可.
如长方形各角相等,但各边不一定相等,菱形各边相等,但各角不一定相等,所以它们都不是正多边形。
判断一个n边形是正n边形的条件
菱形
矩形
正三角形
正方形
合作探究
三角形的内角和等于180°,四边形的内角和是多少度呢?
如图,四边形ABCD的一条对角线AC 把它分成两个三角形,因此四边形的内角和等于这两个三角形的
内角和,
即180°×2=360°.
合作探究
多边形的内角和
教材P35:在下列各个多边形中,任取一个顶点,通过该顶点画出所有对角线,并完成下表.
合作探究
五边形
六边形
七边形
八边形
多边形的内角和
五边形
5
3
(5-2) × 180°
六边形
6
七边形
7
图形 边数
可分成三角形的个数
多边形的内角和
八边形
8
…
…
…
…
n边形
n
4
(6-2) × 180°
(7-2) × 180°
5
(8-2) × 180°
6
n-2
(n-2)×180°
五边形
六边形
七边形
八边形
合作探究
n边形的内角和等于(n-2)· 180°
合作探究
多边形的内角和
(n≥3)
你还可以用其他方法探究n边形的内角和公式吗?
如右图,在n边形内任取一点O,与多边形各顶点连接,把n边形分成n个三角形,用n个三角形的内角和n·180°减去中心的周角360°,得n边形的内角和为(n-2)·180°.
例1(1)十边形的内角和是多少度?
(2)一个多边形的内角和等于1980°,它是几边形?
解 (1)十边形的内角和是
(10-2)×180°= 1440°.
(2)设这个多边形的边数为n,则
(n-2 )×180°= 1980°,
解得n = 13.
所以这是一个十三边形.
学以致用
课堂小结
1、多边形的概念及相关概念;
2、多边形的分类;
3、正多边形的定义;
4、多边形的内角和定理.
作业:P39 A 1、B 5、6.
(1)正十二边形的每一个内角是多少度?
(2)一个多边形的内角和等于1800°,它是几边形?
答:150°.
答:十二边形.
学以致用
过多边形某个顶点的所有对角线,将这个多边形
分成10个三角形,那么这个多边形是几边形?
答:十二边形.
结论:正多边形的每一个内角的度数为:
26
作业
1、教材39页第1、5、题.
2、(2018·聊城中考)如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是 .
180°或360°或540°
练一练:
1、下列叙述正确的是( )
A、每条边都相等的多边形是正多边形。
B、如果画出多边形某一条边所在的直线,这个多边形都在这条直线的同一侧,那么它一定是凹多边形。
C、每个角都相等的多边形叫正多边形。
D、每条边、每个角都相等的多边形叫正多边形。
2、小学学过的下列图形中不可能是正多边形的是( )
A、三角形 B、正方形 C、四边形 D、梯形
D
D
例3:如图,在正方形ABCD中,你能用四种不同的方法把正方形面积四等分吗?
A
B
C
D
分析:
正方形的面积问题一般可以转化为三角形问题,本题也可以直接把正方形四等分.
解:如图所示
例题讲解
填空:
如图,此多边形应记作 边形 ,AB边的邻边是 、 ,顶点E处的内角为 ,过顶点A画出这个多边形的对角线,共有 条,它们把多边形分成 个三角形。
n边形有 个顶点, 条边,有 个角。
四边形有 条对角线。五边形有 条对角线。
四边形的一条对角线将它分成 个三角形.
从五边形的一个顶点出发可以画 条对角线,
它们将五边形分成 个三角形.
正多边形的 相等, 相等.
多边形分为 和 两类.
五
ABCDE
AE
BC
∠AED
2
3
n
n
n
2
5
2
3
2
每条边都
每个角都
凸
凹
AE
BC
三角形
复习回顾
在同一平面内,由不在同一直线上的三条线段首尾顺次连接而成的图形叫作三角形.
三角形的定义:
三角形的边、顶点、内角的概念:
三角形的内角和定理:
三角形的内角和等于180°.
生活中的平面图形
四边形
由这图形你抽象出什么几何图形?
四边形是由不在同一直线上的四条线段首尾顺次连结组成的平面图形.
观察思考
生活中的平面图形
由这图形你抽象出什么几何图形?
五边形
五边形,它是由五条不在同一直线上的线段首尾顺次连结组成的平面图形
观察思考
生活中的平面图形
六边形
由这图形你抽象出什么几何图形?
六边形,它是由不在同一直线上的六条线段首尾顺次连结组成的平面图形.
观察思考
生活中的平面图形
由这图形你抽象出什么几何图形?
八边形
八边形,它是由不在同一直线上的八条线段首尾顺次连结组成的平面图形.
观察思考
生活中的平面图形
湘教版八年级《数学》下册
多边形的概念及内角和
在同一平面内,由不在同一直线上的一些线段首尾顺次相接组成的图形叫做多边形.
多边形的定义
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
抽象概念
……
五边形
六边形
七边形
三角形
四边形
1、在同一平面内;
2、若干条线段;
3、首尾顺次相接;
4、封闭图形.
多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形.
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形.
多边形的定义
抽象概念
内角
对角线
对角线:连接多边形不相邻的两个顶点的线段.
表示方法:五边形ABCDE或五边形AEDCB
A
B
C
D
E
外角
1
多边形的相关概念
顶点
边
抽象概念
n边形有_____个顶点,
_____条边,
_____个内角,
_____个外角,
_____条对角线.
n
n
n
2n
归纳总结1
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
三角形
六边形
四边形
八边形
……..
五边形
请说出下列图形从某一顶点出发的对角线的条数:
多边形的对角线
合作探究
0
1
2
3
5
从同一顶点引出的对角线的条数:
1
2
3
n-3
分割出的三角形的个数:
2
3
4
n-2
0
1
n边形
……
三角形
四边形
五边形
六边形
n边形
……
四边形
合作探究
n边形从一个顶点出发的对角线条数为 条(n≥3);n边形被分成了 个三角形.
n边形共有对角线 条(n≥3)
(n-3)
?
归纳总结2
(n-2)
(1)
(2)
A
B
C
D
E
F
G
H
你能说出这两幅图形的异同点吗?
合作探究
多边形的分类
如图,画出四边形ABCD的任何一条边所在直线,整个四边形都在这条直线的同一侧,这样的四边形叫做凸四边形.
A
B
C
D
合作探究
A
B
D
C
四边形ABCD是凹四边形,因为画出边CD(或BC)所在直线,整个四边形不都在这条直线的同一侧.
凹四边形
多边形的分类
合作探究
正多边形的定义
正方形的各个角都相等,各条边都相等.像正方形这样,在平面内,各个角都相等,各条边都相等的多边形叫做正多边形.
例如:
正三角形
正方形
正五边形
正六边形
合作探究
当n≥3时,必须同时满足以下两个条件:
(1)是各边相等,
(2)是各角相等.
两者缺一不可.
如长方形各角相等,但各边不一定相等,菱形各边相等,但各角不一定相等,所以它们都不是正多边形。
判断一个n边形是正n边形的条件
菱形
矩形
正三角形
正方形
合作探究
三角形的内角和等于180°,四边形的内角和是多少度呢?
如图,四边形ABCD的一条对角线AC 把它分成两个三角形,因此四边形的内角和等于这两个三角形的
内角和,
即180°×2=360°.
合作探究
多边形的内角和
教材P35:在下列各个多边形中,任取一个顶点,通过该顶点画出所有对角线,并完成下表.
合作探究
五边形
六边形
七边形
八边形
多边形的内角和
五边形
5
3
(5-2) × 180°
六边形
6
七边形
7
图形 边数
可分成三角形的个数
多边形的内角和
八边形
8
…
…
…
…
n边形
n
4
(6-2) × 180°
(7-2) × 180°
5
(8-2) × 180°
6
n-2
(n-2)×180°
五边形
六边形
七边形
八边形
合作探究
n边形的内角和等于(n-2)· 180°
合作探究
多边形的内角和
(n≥3)
你还可以用其他方法探究n边形的内角和公式吗?
如右图,在n边形内任取一点O,与多边形各顶点连接,把n边形分成n个三角形,用n个三角形的内角和n·180°减去中心的周角360°,得n边形的内角和为(n-2)·180°.
例1(1)十边形的内角和是多少度?
(2)一个多边形的内角和等于1980°,它是几边形?
解 (1)十边形的内角和是
(10-2)×180°= 1440°.
(2)设这个多边形的边数为n,则
(n-2 )×180°= 1980°,
解得n = 13.
所以这是一个十三边形.
学以致用
课堂小结
1、多边形的概念及相关概念;
2、多边形的分类;
3、正多边形的定义;
4、多边形的内角和定理.
作业:P39 A 1、B 5、6.
(1)正十二边形的每一个内角是多少度?
(2)一个多边形的内角和等于1800°,它是几边形?
答:150°.
答:十二边形.
学以致用
过多边形某个顶点的所有对角线,将这个多边形
分成10个三角形,那么这个多边形是几边形?
答:十二边形.
结论:正多边形的每一个内角的度数为:
26
作业
1、教材39页第1、5、题.
2、(2018·聊城中考)如果一个正方形被截掉一个角后,得到一个多边形,那么这个多边形的内角和是 .
180°或360°或540°
练一练:
1、下列叙述正确的是( )
A、每条边都相等的多边形是正多边形。
B、如果画出多边形某一条边所在的直线,这个多边形都在这条直线的同一侧,那么它一定是凹多边形。
C、每个角都相等的多边形叫正多边形。
D、每条边、每个角都相等的多边形叫正多边形。
2、小学学过的下列图形中不可能是正多边形的是( )
A、三角形 B、正方形 C、四边形 D、梯形
D
D
例3:如图,在正方形ABCD中,你能用四种不同的方法把正方形面积四等分吗?
A
B
C
D
分析:
正方形的面积问题一般可以转化为三角形问题,本题也可以直接把正方形四等分.
解:如图所示
例题讲解
填空:
如图,此多边形应记作 边形 ,AB边的邻边是 、 ,顶点E处的内角为 ,过顶点A画出这个多边形的对角线,共有 条,它们把多边形分成 个三角形。
n边形有 个顶点, 条边,有 个角。
四边形有 条对角线。五边形有 条对角线。
四边形的一条对角线将它分成 个三角形.
从五边形的一个顶点出发可以画 条对角线,
它们将五边形分成 个三角形.
正多边形的 相等, 相等.
多边形分为 和 两类.
五
ABCDE
AE
BC
∠AED
2
3
n
n
n
2
5
2
3
2
每条边都
每个角都
凸
凹
AE
BC
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
