2020-2021学年人教版数学八年级下册17.2勾股定理逆定理课件(22张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册17.2勾股定理逆定理课件(22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 394.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 16:32:13 | ||
图片预览








文档简介
八年级上册(RJ)
17.2勾股定理逆定理
学习目标1
1. 理解勾股定理的逆定理的证明方法并能证明勾股定理的逆定理。
2.掌握勾股定理的逆定理,并能利用勾股定理的逆定理判定一个
三角形是不是直角三角形。
理解勾股定理的逆定理的证明方法并能证明勾股定理的逆定理。
掌握互逆命题、互逆定理、勾股数的概念,理清互逆命题之间的关系
利用勾股定理的逆定理判定一个三角形是不是直角三角形。并会求一个三角形的未知边长、高或面积。
自学释疑、拓展提升
自学问题预设:
1.勾股定理逆定理的内容没理解透彻;
2.勾股定理逆定理的证明方法没弄懂。
教学活动设计:
1.学生典型问题展示:
(1)学案上存在的问题展示;
(2)教材中33页练习1做错学生的错题答案。
学生活动:小组交流,代表展示.
知识点一:勾股定理逆定理及其证明
自学释疑、拓展提升
知识点一:勾股定理逆定理及其证明
文字语言:
几何语言:。
问题解决
方案:教师通过提问、点拨、强调等行为引导学生解决并且进一步理解存在的问题.
你能用文字语言和几何语言分别对勾股定理逆定理进行叙述吗?
自学释疑、拓展提升
教学活动设计:
1.学生典型问题展示:
(1)概念理解不透彻,不能准确地找到命题的条件和结论。
(2)展示课本第33页练习2的错误情况
2.问题解决:
方案:两人一组讨论交流,解决存在的问题。
3.同类题检测:平板推题,巩固练习
说出下列命题的逆命题,并判断原命题和逆命题的真假。
(1)有两个角相等的三角形是等腰三角形。
(2)线段垂直平分线上的点到线段两端的距离相等。
知识点二:互逆命题、互逆定理的概念
判断下列数字是不是勾股数:
(1)5、12、13
(2) 1、√2、3
知识点三:勾股数的概念
教学活动设计:
1.学生典型问题展示:
勾股数概念理解不透彻。
2.问题解决
方案:学生再看课本上的概念,进一步理解。
3.同类题检测:平板推题,巩固练习
自学释疑、拓展提升
知识点四:勾股定理逆定理的简单应用
教学活动设计:
1.学生典型问题展示:
(1)不能准确使用勾股定理逆定理判断一个三角形是否是直角三角形。
(2)<自主学习检测试卷>三道题的准确率,错误情况展示。
2.问题解决方案:
小组帮扶解决不能解决的问题,全班师生共同解决。
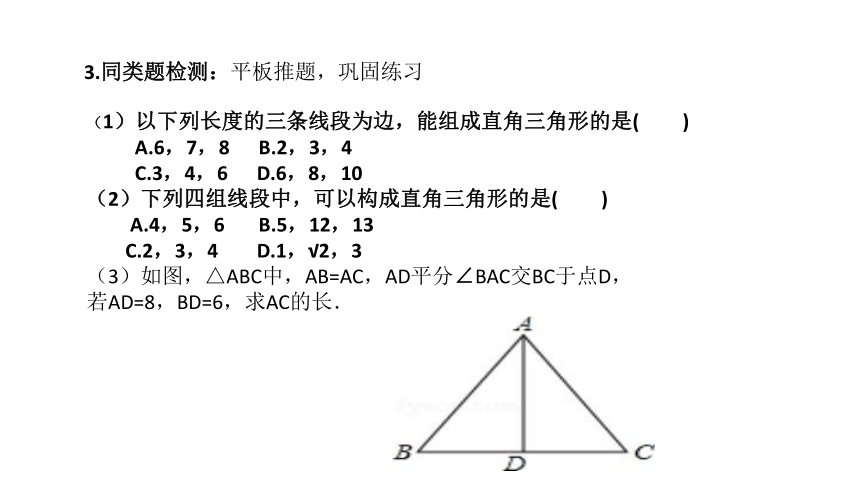
(1)以下列长度的三条线段为边,能组成直角三角形的是( )
A.6,7,8 B.2,3,4
C.3,4,6 D.6,8,10
(2)下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.5,12,13
C.2,3,4 D.1,√2,3
(3)如图,△ABC中,AB=AC,AD平分∠BAC交BC于点D,
若AD=8,BD=6,求AC的长.
3.同类题检测:平板推题,巩固练习
拓展提升:
已知△ABC的三边长分别是a,b,c,且满足a2+b2+c2+50=6a+8b+10c,试判断△ABC是否为直角三角形,并说明理由.
课堂小结
师生活动:学生独立思考,用平板的抢答功能回答问题,教师点 拨补充.
勾股定理逆定理是什么?
什么互逆命题?什么是互逆定理?什么叫勾股数?
3.利用勾股定理逆定理判断三角形是直角三角形时要注意什么?
17.2勾股定理逆定理的应用
学习目标2
1. 理解勾股定理的逆定理的证明方法并能证明勾股定理的逆定理。
2.掌握勾股定理的逆定理,并能利用勾股定理的逆定理判定一个
三角形是不是直角三角形。
1. 通过习题,巩固如何用三角形三边的数量关系来判断三角形的形状。
2. 勾股定理的逆定理的简单应用,体验数形结合思想的应用。
?
自学释疑、拓展提升
知识点一:利用勾股定理逆定理判断一个三角形的形状
自学问题预设:
1.勾股定理逆定理的内容没理解透彻;
2.利用勾股定理逆定理计算三边的关系,判断三角形形状时,易出现计算错误或求两较短边的平方和后,没有通过计算,直接等于第三边的平方。
1.学生典型问题展示:
把学案上第2、3题存在的问题展示。
学生活动:两个同学为一组,相互解决存在的问题。
教师活动:你能用文字语言和几何语言分别对勾股定理逆定理进行叙述吗?
2.问题解决
方案:教师通过提问、点拨、强调等行为引导学生解决并且进一步理解存在的问题.
自学释疑、拓展提升
3.同类题检测:平板推题,巩固练习
下列几组数:
①6,8,10;
②7,24,25;
③9,12,15;
④n2﹣1,2n,n2+1(n是大于1的整数),
其中是勾股数的有( )
A.1组 B.2组 C.3组 D.4组
知识点二:利用勾股定理逆定理判断三角形形状后,再求三角形未知边长、高、面积或周长等
3.同类题检测:平板推题,巩固练习
三角形的三边长分别为6,8,10,则斜边上的高为( )
A.4.8 B.6 C.8 D.2.4
1.学生典型问题展示:
把学案上第4题存在的问题展示。
学生活动:小组交流,代表展示.
2.问题解决
方案:学生代表展示,其他同学适当补充、质疑。
自学释疑、拓展提升
1.学生典型问题展示:
把学案上第5题存在的问题展示。
学生活动:小组交流,代表展示.
2.问题解决
方案:学生通过小组合作交流,解决存在的问题,教师适当引导、点拨。
3.同类题检测:平板推题,巩固练习
如图,在单位正方形组成的网格图中标有AB、CD、EF、GH
四条线段,其中能构成一个直角三角形三边的线段是( )
A.CD、EF、GH B.AB、EF、GH
C.AB、CD、GH D.AB、CD、EF
知识三:勾股定理逆定理在正方形网格中的应用
自学释疑、拓展提升
知识四:勾股定理逆定理与具有非负性式子的应用
1.学生典型问题展示:
把学案上第6题存在的问题展示。
学生活动:小组交流,代表展示.
2.问题解决
方案:学生代表展示,其他同学适当补充、质疑。
3.同类题检测:平板推题,巩固练习
如果一个三角形的三边长a,b,c满足(a-b)2+|b-2|+(c2-8)2=0,
那么此三角形为(??)
A.等边三角形 B.等腰三角形
C.等腰直角三角形 D.直角三角形
自学释疑、拓展提升
.
知识五:勾股定理逆定理在实践生活中的应用
1.学生典型问题展示:
把学案上第1、7、8题存在的问题展示。
学生活动:小组交流,代表展示.
2.问题解决
方案:小组帮扶解决,不能解决的问题,全班师生共同解决。。
3.同类题检测:平板推题,巩固练习
甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,
甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B
两点的直线距离为1000m,甲客轮沿着北偏东30?的方向航行,
则乙客轮的航行方向可能是( )
A.北偏西30? B.南偏西30?
C.南偏东60? D.南偏西60?
拓展提升
已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,
试判断△ABC的形状.小明的解法为:
解:因为a2c2-b2c2=a4-b4,?……①
所以c2(a2-b2)=(a2+b2)(a2-b2).?……②
所以c2=a2+b2,?……③
即△ABC是直角三角形.
请问:
上述解题过程,从哪一步开始出现错误?
请写出该步的代号:? ? ? ? ?;
(2)错误的原因为:? ? ? ? ? ? ? ? ? ? ? ? ??;
(3)写出本题正确的结论,并说明理由.
?
课后作业:
课本习题第34页第3、4题
课堂总结
课堂总结
师生活动:学生独立思考,用平板的抢答功能回答问题,教师点拨补充.
17.2勾股定理逆定理
学习目标1
1. 理解勾股定理的逆定理的证明方法并能证明勾股定理的逆定理。
2.掌握勾股定理的逆定理,并能利用勾股定理的逆定理判定一个
三角形是不是直角三角形。
理解勾股定理的逆定理的证明方法并能证明勾股定理的逆定理。
掌握互逆命题、互逆定理、勾股数的概念,理清互逆命题之间的关系
利用勾股定理的逆定理判定一个三角形是不是直角三角形。并会求一个三角形的未知边长、高或面积。
自学释疑、拓展提升
自学问题预设:
1.勾股定理逆定理的内容没理解透彻;
2.勾股定理逆定理的证明方法没弄懂。
教学活动设计:
1.学生典型问题展示:
(1)学案上存在的问题展示;
(2)教材中33页练习1做错学生的错题答案。
学生活动:小组交流,代表展示.
知识点一:勾股定理逆定理及其证明
自学释疑、拓展提升
知识点一:勾股定理逆定理及其证明
文字语言:
几何语言:。
问题解决
方案:教师通过提问、点拨、强调等行为引导学生解决并且进一步理解存在的问题.
你能用文字语言和几何语言分别对勾股定理逆定理进行叙述吗?
自学释疑、拓展提升
教学活动设计:
1.学生典型问题展示:
(1)概念理解不透彻,不能准确地找到命题的条件和结论。
(2)展示课本第33页练习2的错误情况
2.问题解决:
方案:两人一组讨论交流,解决存在的问题。
3.同类题检测:平板推题,巩固练习
说出下列命题的逆命题,并判断原命题和逆命题的真假。
(1)有两个角相等的三角形是等腰三角形。
(2)线段垂直平分线上的点到线段两端的距离相等。
知识点二:互逆命题、互逆定理的概念
判断下列数字是不是勾股数:
(1)5、12、13
(2) 1、√2、3
知识点三:勾股数的概念
教学活动设计:
1.学生典型问题展示:
勾股数概念理解不透彻。
2.问题解决
方案:学生再看课本上的概念,进一步理解。
3.同类题检测:平板推题,巩固练习
自学释疑、拓展提升
知识点四:勾股定理逆定理的简单应用
教学活动设计:
1.学生典型问题展示:
(1)不能准确使用勾股定理逆定理判断一个三角形是否是直角三角形。
(2)<自主学习检测试卷>三道题的准确率,错误情况展示。
2.问题解决方案:
小组帮扶解决不能解决的问题,全班师生共同解决。
(1)以下列长度的三条线段为边,能组成直角三角形的是( )
A.6,7,8 B.2,3,4
C.3,4,6 D.6,8,10
(2)下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.5,12,13
C.2,3,4 D.1,√2,3
(3)如图,△ABC中,AB=AC,AD平分∠BAC交BC于点D,
若AD=8,BD=6,求AC的长.
3.同类题检测:平板推题,巩固练习
拓展提升:
已知△ABC的三边长分别是a,b,c,且满足a2+b2+c2+50=6a+8b+10c,试判断△ABC是否为直角三角形,并说明理由.
课堂小结
师生活动:学生独立思考,用平板的抢答功能回答问题,教师点 拨补充.
勾股定理逆定理是什么?
什么互逆命题?什么是互逆定理?什么叫勾股数?
3.利用勾股定理逆定理判断三角形是直角三角形时要注意什么?
17.2勾股定理逆定理的应用
学习目标2
1. 理解勾股定理的逆定理的证明方法并能证明勾股定理的逆定理。
2.掌握勾股定理的逆定理,并能利用勾股定理的逆定理判定一个
三角形是不是直角三角形。
1. 通过习题,巩固如何用三角形三边的数量关系来判断三角形的形状。
2. 勾股定理的逆定理的简单应用,体验数形结合思想的应用。
?
自学释疑、拓展提升
知识点一:利用勾股定理逆定理判断一个三角形的形状
自学问题预设:
1.勾股定理逆定理的内容没理解透彻;
2.利用勾股定理逆定理计算三边的关系,判断三角形形状时,易出现计算错误或求两较短边的平方和后,没有通过计算,直接等于第三边的平方。
1.学生典型问题展示:
把学案上第2、3题存在的问题展示。
学生活动:两个同学为一组,相互解决存在的问题。
教师活动:你能用文字语言和几何语言分别对勾股定理逆定理进行叙述吗?
2.问题解决
方案:教师通过提问、点拨、强调等行为引导学生解决并且进一步理解存在的问题.
自学释疑、拓展提升
3.同类题检测:平板推题,巩固练习
下列几组数:
①6,8,10;
②7,24,25;
③9,12,15;
④n2﹣1,2n,n2+1(n是大于1的整数),
其中是勾股数的有( )
A.1组 B.2组 C.3组 D.4组
知识点二:利用勾股定理逆定理判断三角形形状后,再求三角形未知边长、高、面积或周长等
3.同类题检测:平板推题,巩固练习
三角形的三边长分别为6,8,10,则斜边上的高为( )
A.4.8 B.6 C.8 D.2.4
1.学生典型问题展示:
把学案上第4题存在的问题展示。
学生活动:小组交流,代表展示.
2.问题解决
方案:学生代表展示,其他同学适当补充、质疑。
自学释疑、拓展提升
1.学生典型问题展示:
把学案上第5题存在的问题展示。
学生活动:小组交流,代表展示.
2.问题解决
方案:学生通过小组合作交流,解决存在的问题,教师适当引导、点拨。
3.同类题检测:平板推题,巩固练习
如图,在单位正方形组成的网格图中标有AB、CD、EF、GH
四条线段,其中能构成一个直角三角形三边的线段是( )
A.CD、EF、GH B.AB、EF、GH
C.AB、CD、GH D.AB、CD、EF
知识三:勾股定理逆定理在正方形网格中的应用
自学释疑、拓展提升
知识四:勾股定理逆定理与具有非负性式子的应用
1.学生典型问题展示:
把学案上第6题存在的问题展示。
学生活动:小组交流,代表展示.
2.问题解决
方案:学生代表展示,其他同学适当补充、质疑。
3.同类题检测:平板推题,巩固练习
如果一个三角形的三边长a,b,c满足(a-b)2+|b-2|+(c2-8)2=0,
那么此三角形为(??)
A.等边三角形 B.等腰三角形
C.等腰直角三角形 D.直角三角形
自学释疑、拓展提升
.
知识五:勾股定理逆定理在实践生活中的应用
1.学生典型问题展示:
把学案上第1、7、8题存在的问题展示。
学生活动:小组交流,代表展示.
2.问题解决
方案:小组帮扶解决,不能解决的问题,全班师生共同解决。。
3.同类题检测:平板推题,巩固练习
甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,
甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B
两点的直线距离为1000m,甲客轮沿着北偏东30?的方向航行,
则乙客轮的航行方向可能是( )
A.北偏西30? B.南偏西30?
C.南偏东60? D.南偏西60?
拓展提升
已知a,b,c为△ABC的三边,且满足a2c2-b2c2=a4-b4,
试判断△ABC的形状.小明的解法为:
解:因为a2c2-b2c2=a4-b4,?……①
所以c2(a2-b2)=(a2+b2)(a2-b2).?……②
所以c2=a2+b2,?……③
即△ABC是直角三角形.
请问:
上述解题过程,从哪一步开始出现错误?
请写出该步的代号:? ? ? ? ?;
(2)错误的原因为:? ? ? ? ? ? ? ? ? ? ? ? ??;
(3)写出本题正确的结论,并说明理由.
?
课后作业:
课本习题第34页第3、4题
课堂总结
课堂总结
师生活动:学生独立思考,用平板的抢答功能回答问题,教师点拨补充.
