20.3 一次函数的应用课时训练(含答案)
文档属性
| 名称 | 20.3 一次函数的应用课时训练(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三节一次函数的应用课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为预防新冠病毒,某学校每周末用药熏消毒法对教室进行消毒,已知药物释放过程中,教室内每立方米空气中含药量与时间成正比例;药物释放完毕后,与成反比例,如图所示.根据图象信息,下列选项错误的是( )
A.药物释放过程需要小时
B.药物释放过程中,与的函数表达式是
C.空气中含药量大于等于的时间为
D.若当空气中含药量降低到以下时对身体无害,那么从消毒开始,至少需要经过4.5小时学生才能进入教室
2.某口罩生产企业于2020年1月份开始了技术改造,其月利润(万元)与月份之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为45万元
B.改造完成后每月利润比前一个月增加30万元
C.改造完成前后共有5个月的利润低于135万元
D.9月份该企业利润达到205万元
3.如图,在平面直角坐标系中,O为坐标原点,直线与x轴交于B点,与轴交于A点,点在线段 上,且,若点P在坐标轴上,则满足的点P的个数是( )
A.4 B.3 C.2 D.1
4.一次函数的图像与轴、轴交于两点,点是坐标平面内直线外一点,过点作轴的平行线交直线于点,过点作轴的平行线交直线于点,则( )
A. B. C. D.
5.如图,直线和直线相交于点,根据图象可知,方程组的解是( )
A. B. C. D.
6.如图,A、M、N三点坐标分别为A(0,1),M(3,4),N(5,6),动点P从点A出发,沿y轴以每秒一个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒,若点M、N分别位于l的异侧,则t的取值范围是( )
A. B. C. D.
7.直线kx-3y=8,2x+5y=-4交点的纵坐标为0,则k的值为( )
A.4 B.﹣4 C.2 D.-2
8.如图,一次函数的图像与轴,轴分别交于点,点,过点作直线将分成周长相等的两部分,则直线的函数表达式为( )
A. B. C. D.
9.某游泳馆新推出了甲、乙两种消费卡,设游泳次数为时两种消费卡所需费用分别为,元,,与的函数图象如图所示,当游泳次数为30次时选择哪种消费卡更合算( )
A.甲种更合算 B.乙种更合算 C.两种一样合算 D.无法确定
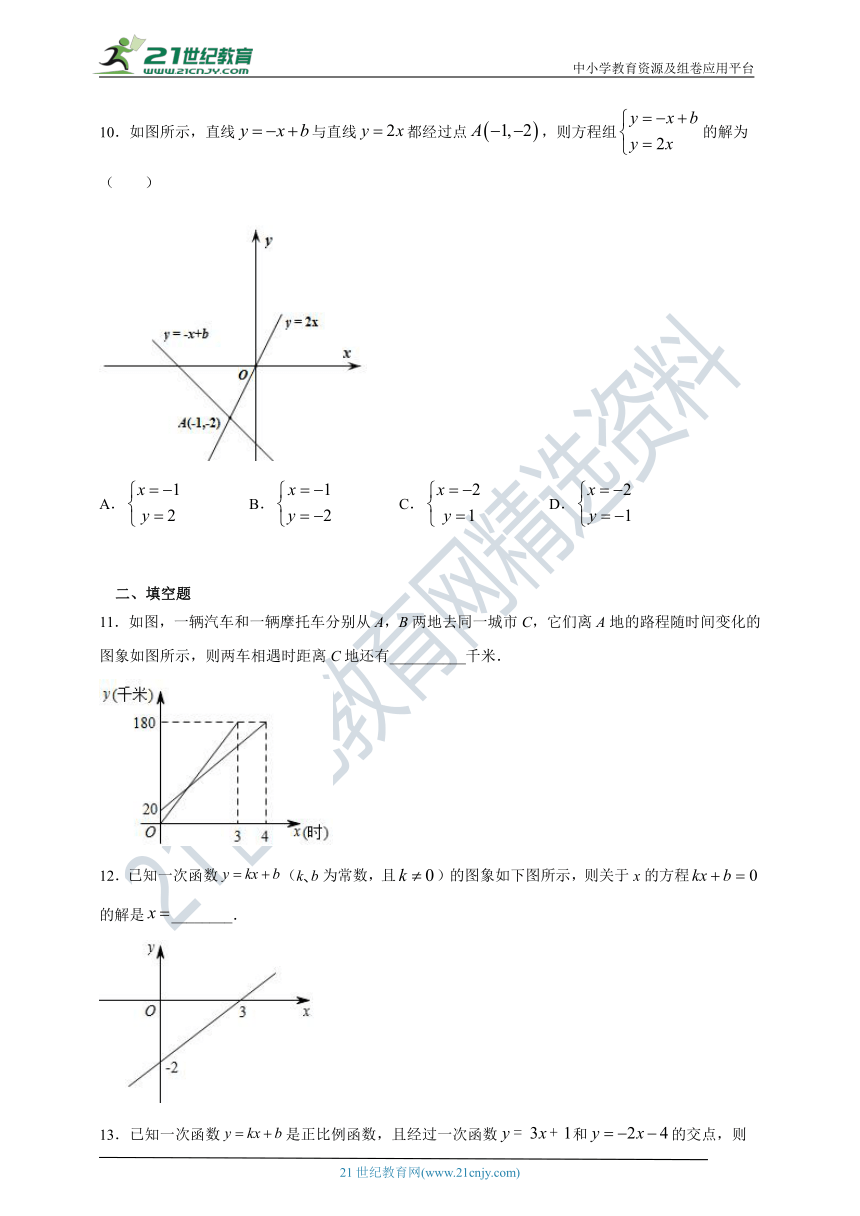
10.如图所示,直线与直线都经过点,则方程组的解为( )
A. B. C. D.
二、填空题
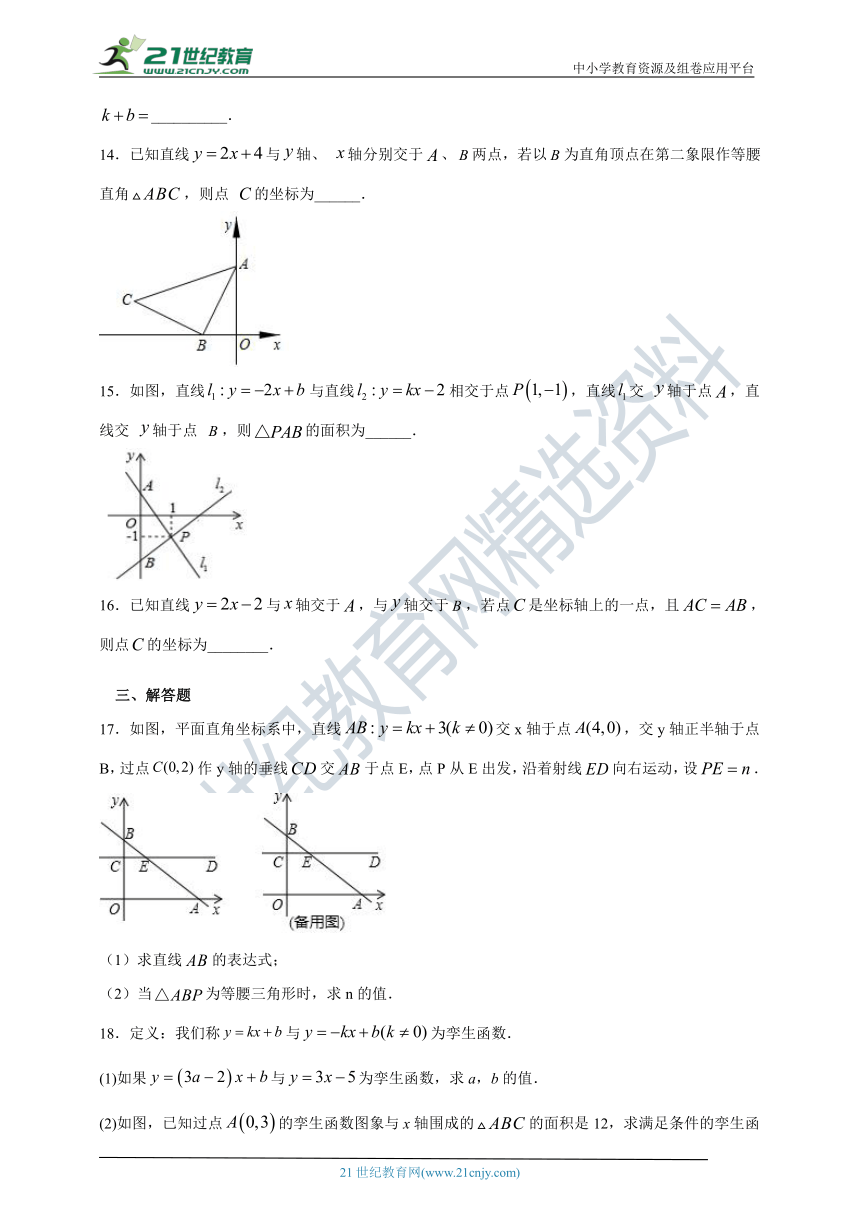
11.如图,一辆汽车和一辆摩托车分别从A,B两地去同一城市C,它们离A地的路程随时间变化的图象如图所示,则两车相遇时距离C地还有__________千米.
12.已知一次函数(k?b为常数,且)的图象如下图所示,则关于x的方程的解是________.
13.已知一次函数是正比例函数,且经过一次函数和的交点,则__________.
14.已知直线与轴、 轴分别交于、两点,若以为直角顶点在第二象限作等腰直角,则点 的坐标为______.
15.如图,直线与直线相交于点,直线交 轴于点,直线交 轴于点 ,则的面积为______.
16.已知直线与轴交于,与轴交于,若点是坐标轴上的一点,且,则点的坐标为________.
三、解答题
17.如图,平面直角坐标系中,直线交x轴于点,交y轴正半轴于点B,过点作y轴的垂线交于点E,点P从E出发,沿着射线向右运动,设.
(1)求直线的表达式;
(2)当为等腰三角形时,求n的值.
18.定义:我们称与为孪生函数.
(1)如果与为孪生函数,求a,b的值.
(2)如图,已知过点的孪生函数图象与x轴围成的的面积是12,求满足条件的孪生函数.
19.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,已知,点是第一象限内在直线上一点.
(1)直接写出,的值;
(2)设,求的面积与的函数解析式;
(3)当是等腰三角形,求点的坐标.
20.计算:
(1);
(2)已知,求的立方根;
(3)如图,一次函数的图像分别与轴、轴交于点、,且经过点,求的面积.
参考答案
1.D
2.D
3.A
4.B
5.C
6.C
7.B
8.D
9.B
10.B.
11.120
12.3
13.2
14.(-6,2)
15.
16.、、
解:令,得到,
,
令,得到,
,
,,
,
以为圆心,长为半径作圆,交坐标轴即为点,
,
,,,或,
故答案为:、、.
.
17.(1);(2)或或
解:将点的坐标代入直线并解得:,
故的表达式为:;
(2)当时,,故点,,则点,,
而点、坐标分别为:、,
则;,,
当时,,解得:;
当时,同理可得:(不合题意值已舍去);
当时,同理可得:;
故或或..
18.(1),;(2)
解:(1)由题意得:,
,解得,
∴,;
(2)由题意得:过点A的李生函数为,
令时,,
∴,
,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴直线的表达式为,直线的表达式为,
∴过点A的孪生函数为.
19.(1)k=-1,b=6;(2)S=;(3)(0,6)或(3,3)或(6-,)
解:(1)∵OA=OB=6,
∴A(6,0),B(0,6),代入y=kx+b中,
,解得:;
(2)∵点P在直线y=-x+6上,
设点P的坐标为(x,-x+6),
∴△OPA的面积为S==;
(3)当OP=OA时,
点P与点B重合,即P(0,6);
当PA=PO时,
点P在OA的垂直平分线上,
∴点P的横坐标为3,代入y=-x+6上,
则y=3,即P(3,3);
当AP=AO时,AP=6,
过点P作PC⊥OA,
∵OA=OB,
∴△OAB是等腰直角三角形,即∠OAB=45°,
∴△PCA是直角三角形,
∴AC=PC,又AP=AO=6,
∴AC=PC==,
∴OC=OA-AC=6-,
∴点P(6-,),
综上:点P的坐标为(0,6)或(3,3)或(6-,).
20.(1);(2);(3).
解:(1)原式=;
(2)∵,
∴,
∴,,
∴,
∴,
∴;
∴的立方根为;
(3)由图像可得点B的坐标为,然后把点和点代入一次函数得:
,解得:,
∴一次函数的解析式为,
令y=0时,则有,解得:,
∴OA=2,OB=3,
∴.
_21?????????è?????(www.21cnjy.com)_
第三节一次函数的应用课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.为预防新冠病毒,某学校每周末用药熏消毒法对教室进行消毒,已知药物释放过程中,教室内每立方米空气中含药量与时间成正比例;药物释放完毕后,与成反比例,如图所示.根据图象信息,下列选项错误的是( )
A.药物释放过程需要小时
B.药物释放过程中,与的函数表达式是
C.空气中含药量大于等于的时间为
D.若当空气中含药量降低到以下时对身体无害,那么从消毒开始,至少需要经过4.5小时学生才能进入教室
2.某口罩生产企业于2020年1月份开始了技术改造,其月利润(万元)与月份之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为45万元
B.改造完成后每月利润比前一个月增加30万元
C.改造完成前后共有5个月的利润低于135万元
D.9月份该企业利润达到205万元
3.如图,在平面直角坐标系中,O为坐标原点,直线与x轴交于B点,与轴交于A点,点在线段 上,且,若点P在坐标轴上,则满足的点P的个数是( )
A.4 B.3 C.2 D.1
4.一次函数的图像与轴、轴交于两点,点是坐标平面内直线外一点,过点作轴的平行线交直线于点,过点作轴的平行线交直线于点,则( )
A. B. C. D.
5.如图,直线和直线相交于点,根据图象可知,方程组的解是( )
A. B. C. D.
6.如图,A、M、N三点坐标分别为A(0,1),M(3,4),N(5,6),动点P从点A出发,沿y轴以每秒一个单位长度的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒,若点M、N分别位于l的异侧,则t的取值范围是( )
A. B. C. D.
7.直线kx-3y=8,2x+5y=-4交点的纵坐标为0,则k的值为( )
A.4 B.﹣4 C.2 D.-2
8.如图,一次函数的图像与轴,轴分别交于点,点,过点作直线将分成周长相等的两部分,则直线的函数表达式为( )
A. B. C. D.
9.某游泳馆新推出了甲、乙两种消费卡,设游泳次数为时两种消费卡所需费用分别为,元,,与的函数图象如图所示,当游泳次数为30次时选择哪种消费卡更合算( )
A.甲种更合算 B.乙种更合算 C.两种一样合算 D.无法确定
10.如图所示,直线与直线都经过点,则方程组的解为( )
A. B. C. D.
二、填空题
11.如图,一辆汽车和一辆摩托车分别从A,B两地去同一城市C,它们离A地的路程随时间变化的图象如图所示,则两车相遇时距离C地还有__________千米.
12.已知一次函数(k?b为常数,且)的图象如下图所示,则关于x的方程的解是________.
13.已知一次函数是正比例函数,且经过一次函数和的交点,则__________.
14.已知直线与轴、 轴分别交于、两点,若以为直角顶点在第二象限作等腰直角,则点 的坐标为______.
15.如图,直线与直线相交于点,直线交 轴于点,直线交 轴于点 ,则的面积为______.
16.已知直线与轴交于,与轴交于,若点是坐标轴上的一点,且,则点的坐标为________.
三、解答题
17.如图,平面直角坐标系中,直线交x轴于点,交y轴正半轴于点B,过点作y轴的垂线交于点E,点P从E出发,沿着射线向右运动,设.
(1)求直线的表达式;
(2)当为等腰三角形时,求n的值.
18.定义:我们称与为孪生函数.
(1)如果与为孪生函数,求a,b的值.
(2)如图,已知过点的孪生函数图象与x轴围成的的面积是12,求满足条件的孪生函数.
19.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,已知,点是第一象限内在直线上一点.
(1)直接写出,的值;
(2)设,求的面积与的函数解析式;
(3)当是等腰三角形,求点的坐标.
20.计算:
(1);
(2)已知,求的立方根;
(3)如图,一次函数的图像分别与轴、轴交于点、,且经过点,求的面积.
参考答案
1.D
2.D
3.A
4.B
5.C
6.C
7.B
8.D
9.B
10.B.
11.120
12.3
13.2
14.(-6,2)
15.
16.、、
解:令,得到,
,
令,得到,
,
,,
,
以为圆心,长为半径作圆,交坐标轴即为点,
,
,,,或,
故答案为:、、.
.
17.(1);(2)或或
解:将点的坐标代入直线并解得:,
故的表达式为:;
(2)当时,,故点,,则点,,
而点、坐标分别为:、,
则;,,
当时,,解得:;
当时,同理可得:(不合题意值已舍去);
当时,同理可得:;
故或或..
18.(1),;(2)
解:(1)由题意得:,
,解得,
∴,;
(2)由题意得:过点A的李生函数为,
令时,,
∴,
,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴直线的表达式为,直线的表达式为,
∴过点A的孪生函数为.
19.(1)k=-1,b=6;(2)S=;(3)(0,6)或(3,3)或(6-,)
解:(1)∵OA=OB=6,
∴A(6,0),B(0,6),代入y=kx+b中,
,解得:;
(2)∵点P在直线y=-x+6上,
设点P的坐标为(x,-x+6),
∴△OPA的面积为S==;
(3)当OP=OA时,
点P与点B重合,即P(0,6);
当PA=PO时,
点P在OA的垂直平分线上,
∴点P的横坐标为3,代入y=-x+6上,
则y=3,即P(3,3);
当AP=AO时,AP=6,
过点P作PC⊥OA,
∵OA=OB,
∴△OAB是等腰直角三角形,即∠OAB=45°,
∴△PCA是直角三角形,
∴AC=PC,又AP=AO=6,
∴AC=PC==,
∴OC=OA-AC=6-,
∴点P(6-,),
综上:点P的坐标为(0,6)或(3,3)或(6-,).
20.(1);(2);(3).
解:(1)原式=;
(2)∵,
∴,
∴,,
∴,
∴,
∴;
∴的立方根为;
(3)由图像可得点B的坐标为,然后把点和点代入一次函数得:
,解得:,
∴一次函数的解析式为,
令y=0时,则有,解得:,
∴OA=2,OB=3,
∴.
_21?????????è?????(www.21cnjy.com)_
