2020-2021学年沪教版数学八年级下册第22章四边形 单元试卷(word解析版)
文档属性
| 名称 | 2020-2021学年沪教版数学八年级下册第22章四边形 单元试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 520.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 18:03:47 | ||
图片预览


文档简介
第22章四边形
一、选择题
如图所示,一个
角的三角形纸片,剪去这个
角后,得到一个四边形,则
的度数为
A.
B.
C.
D.
课外活动时,王老师让同学们做一个对角线互相垂直的等腰梯形形状的风筝,其面积为
,则两条对角线所用的竹条至少需
A.
B.
C.
D.
若等腰梯形两底之差等于一腰的
倍,则这个梯形的一个底角为
A.
B.
C.
D.
已知直角梯形
中,,,,,
分别是
,
边的中点,连接
,
交于点
,连接
并延长交
于点
,连接
,则下列结论不正确的是
A.
平分
B.四边形
为平行四边形
C.
将直角梯形分为面积相等的两部分
D.
为等腰三角形
如图是一块长方形的场地,长,宽,从、两处入口的中路宽都为,两小路汇合处路宽为,其余部分种植草坪,则草坪面积为
A.
B.
C.
D.
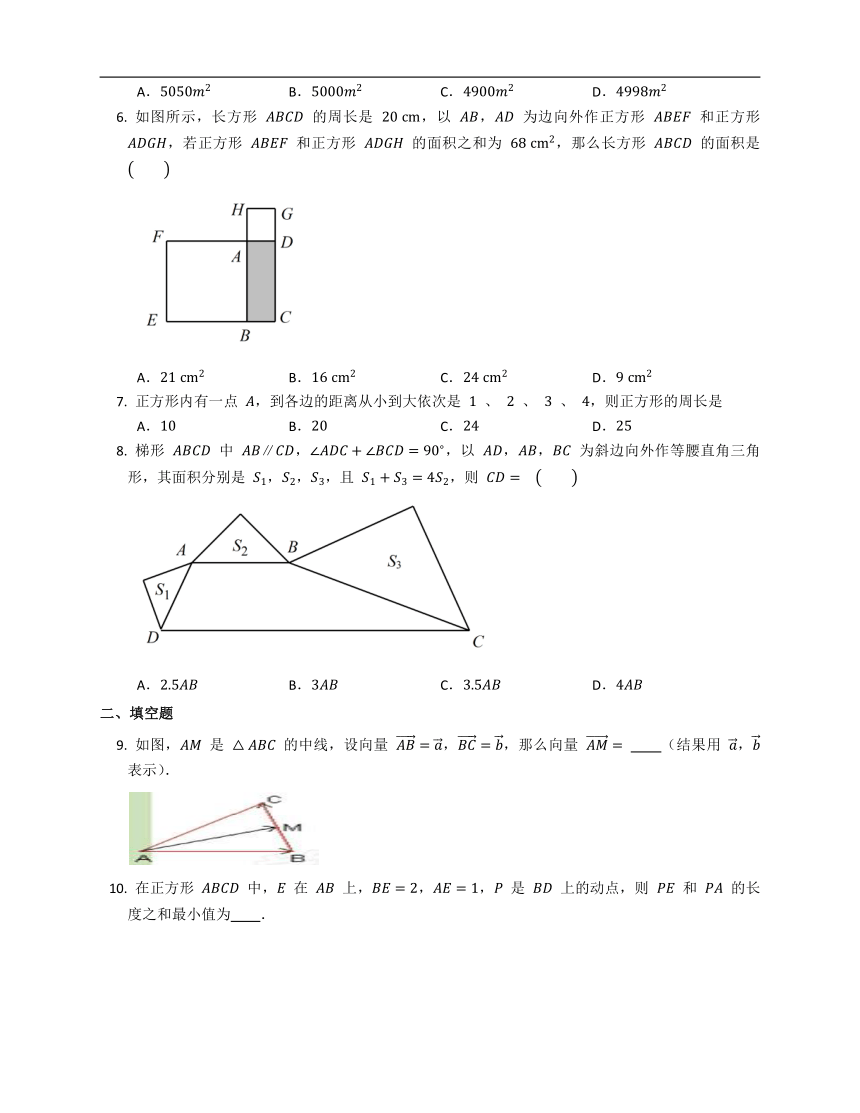
如图所示,长方形
的周长是
,以
,
为边向外作正方形
和正方形
,若正方形
和正方形
的面积之和为
,那么长方形
的面积是
A.
B.
C.
D.
正方形内有一点
,到各边的距离从小到大依次是
、
、
、
,则正方形的周长是
A.
B.
C.
D.
梯形
中
,,以
,,
为斜边向外作等腰直角三角形,其面积分别是
,,,且
,则
A.
B.
C.
D.
二、填空题
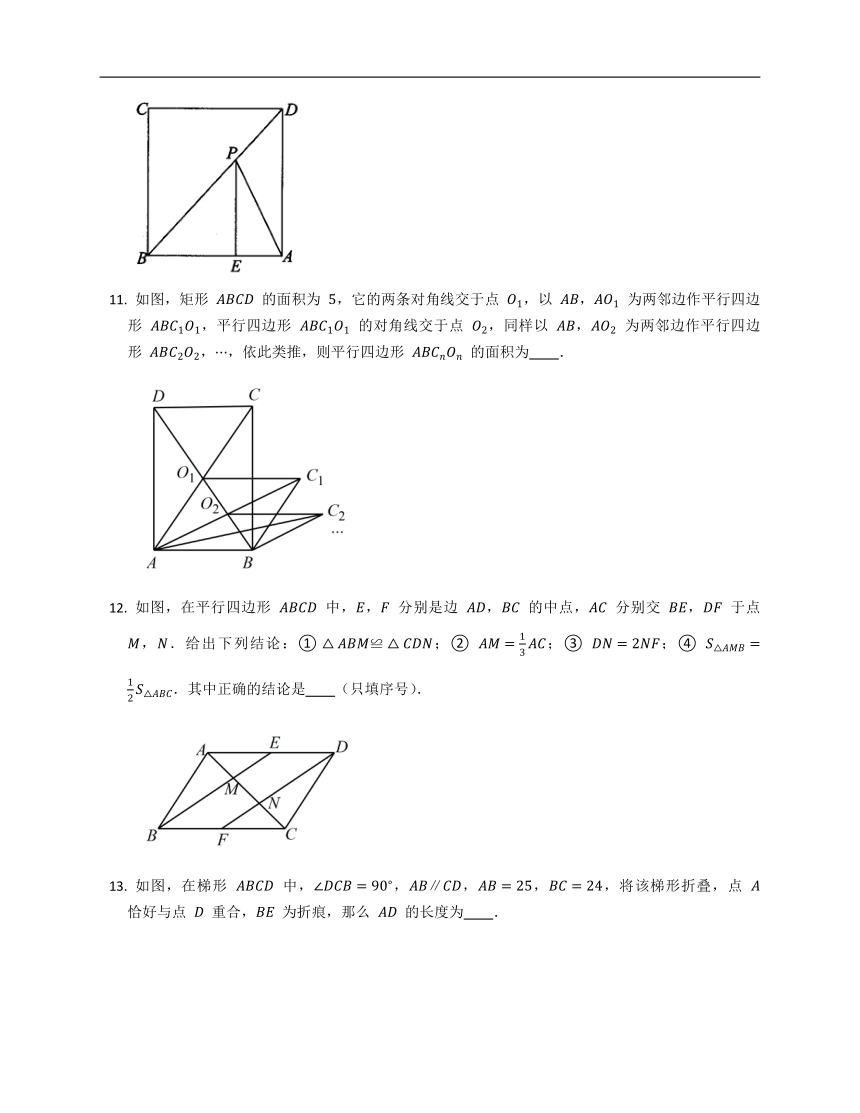
如图,
是
的中线,设向量
,,那么向量
(结果用
,
表示).
在正方形
中,
在
上,,,
是
上的动点,则
和
的长度之和最小值为
.
如图,矩形
的面积为
,它的两条对角线交于点
,以
,
为两邻边作平行四边形
,平行四边形
的对角线交于点
,同样以
,
为两邻边作平行四边形
,,依此类推,则平行四边形
的面积为
.
如图,在平行四边形
中,,
分别是边
,
的中点,
分别交
,
于点
,.给出下列结论:①
;②
;③
;④
.其中正确的结论是
(只填序号).
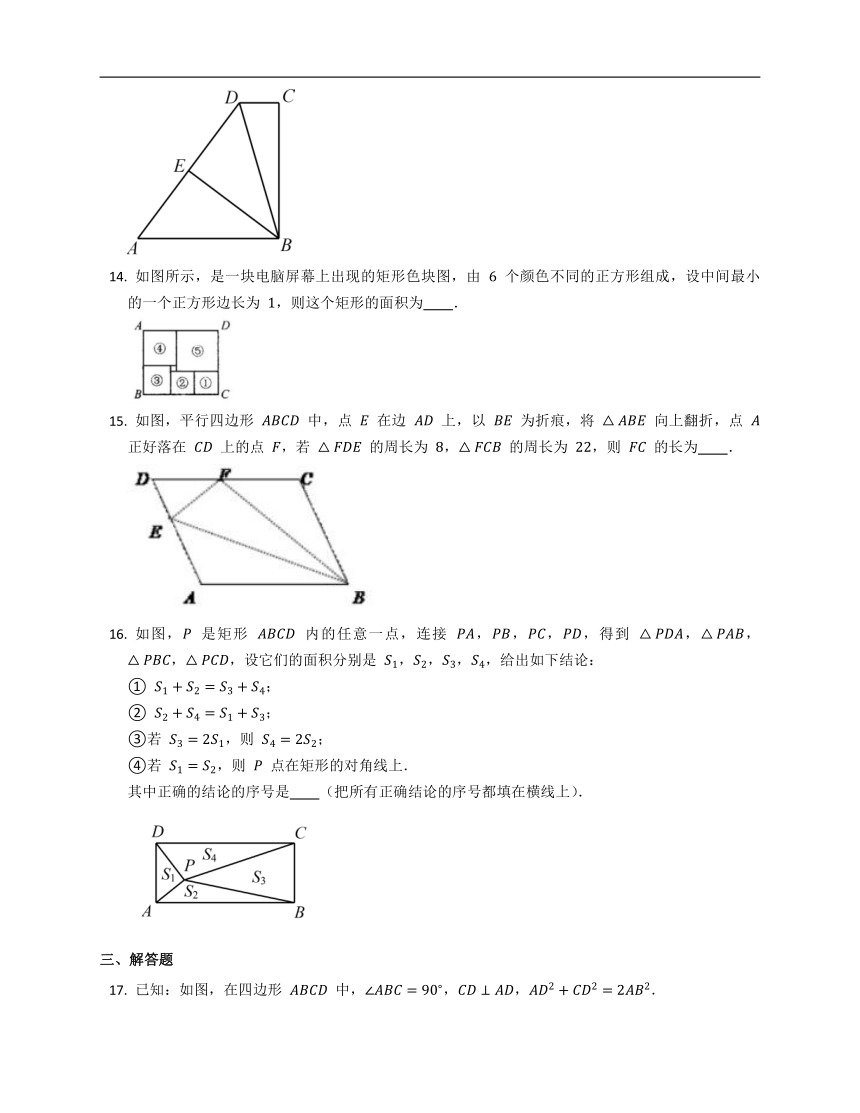
如图,在梯形
中,,,,,将该梯形折叠,点
恰好与点
重合,
为折痕,那么
的长度为
.
如图所示,是一块电脑屏幕上出现的矩形色块图,由
个颜色不同的正方形组成,设中间最小的一个正方形边长为
,则这个矩形的面积为
.
如图,平行四边形
中,点
在边
上,以
为折痕,将
向上翻折,点
正好落在
上的点
,若
的周长为
,
的周长为
,则
的长为
.
如图,
是矩形
内的任意一点,连接
,,,,得到
,,,,设它们的面积分别是
,,,,给出如下结论:
①
;
②
;
③若
,则
;
④若
,则
点在矩形的对角线上.
其中正确的结论的序号是
(把所有正确结论的序号都填在横线上).
三、解答题
已知:如图,在四边形
中,,,.
(1)
求证:;
(2)
当
于
时,试证明:.
如图,在梯形纸片
中,,,将纸片沿过点
的直线折叠,使点
落在
上的点
处,折痕
交
于点
,连接
.
(1)
求证:四边形
是菱形;
(2)
若
,试判断四边形
的形状,并加以证明.
探究问题:
(1)
方法感悟:
如图①,在正方形
中,点
,
分别为
,
边上的点,且满足
,连接
,求证
.
感悟解题方法,并完成下列填空:
将
绕点
顺时针旋转
得到
,此时
与
重合,
由旋转可得:,,,,
,
因此,点
,,
在同一条直线上.
,
.
,,即
.
又
,,
.
,故
.
(2)
方法迁移:
如图②,将
沿斜边翻折得到
,点
,
分别为
,
边上的点,且
.试猜想
,,
之间有何数量关系,并证明你的猜想.
在平行四边形
中,
的平分线交直线
于点
,交直线
于点
.
(1)
在图
中证明
;
(2)
若
,
是
的中点(如图
),直接写出
的度数;
(3)
若
,,,分别连接
,(如图
),求
的度数.
答案
一、选择题
1.
【答案】C
2.
【答案】C
【解析】如图.
且
,
又
等腰梯形
的面积为
,
,解得
.
3.
【答案】C
【解析】如图,,设
,则
,作过点
,
的高
,,
则四边形
为矩形,
.
等腰梯形是轴对称图形,
,
,
.
4.
【答案】C
【解析】本题可用排除法解题,由题意易证
,得
,
.
.
.
.
选项
A
正确;
且
,
四边形
为平行四边形,选项
B
正确;
,,
,即选项
D
正确.
5.
【答案】B
【解析】【分析】根据已知将道路平移,再利用矩形的性质求出长和宽,再进行解答.
【解析】解:由图可知:矩形中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:米,宽为米.
所以草坪的面积应该是长宽米.
故选:.
【点评】此题考查了生活中的平移,根据图形得出草坪正好可以拼成一个长方形是解题关键.
6.
【答案】B
【解析】设
,,则正方形
的面积为
,正方形
的面积为
,可列出方程为
,解得
,.若
,则
;若
,则
.此时长方形
的面积均为
.
7.
【答案】B
8.
【答案】B
二、填空题
9.
【答案】
【解析】
是
的中线,,
,
,
.
10.
【答案】
【解析】连接
,,
与
交于点
,
此时
的最小,即
就是
的长度.
正方形
中,,,
,
.
11.
【答案】
12.
【答案】①②③
【解析】在平行四边形
中,,,
又
,
分别是边
,
的中点,
,,
四边形
是平行四边形,
,
,
,,
;
是
的中点,,
是
的中点,
同理
是
的中点,
,
;
.不成立,
正确的结论是①②③.
13.
【答案】
【解析】过点
作
,垂足为
,
根据题意,,
,
在
中,由勾股定理得,.
14.
【答案】
【解析】设右下角的小正方形①边长为
,则②③④⑤边长分别为
,,,.矩形的长(下边),矩形的长(上边),则
,
解得
,
②③④⑤边长分别为
,,,,
矩形的长
,宽
,
面积
.
15.
【答案】
【解析】设
,,
平行四边形
,
,,
为折痕,
,,
周长为
,
的周长为
,
,,
,解得
.
16.
【答案】②④
【解析】过点
分别向
,
作垂线段,两个三角形的面积之和等于矩形面积的一半,同理,过点
分别向
,
作垂线段,两个三角形的面积之和等于矩形面积的一半.
.
又
,.
所以成立的答案是②④.
三、解答题
17.
【答案】
(1)
连接
.
,
.
,
.
,
.
.
(2)
过
作
于
.
,
四边形
是矩形.
.
,,
.
又
,,
.
.
.
18.
【答案】
(1)
依题意
,,,
,
.
.
.
故
,四边形
是菱形.
(2)
四边形
为平行四边形.
证明:
,
又
,
.
又
,
.
又
,可得
.
四边形
为平行四边形.
19.
【答案】
(1)
;;
(2)
.理由如下:
假设
的度数为
,将
绕点
顺时针旋转
得到
,如图,此时
与
重合,
由旋转可得:,,,,
,
因此,点
,,
在同一条直线上.
,
.
,
,即
.
在
和
中,
.
.
又
,
.
【解析】
(1)
如图①所示;
根据等量代换得出
,
利用
得出
,
.
20.
【答案】
(1)
如图
,
平分
,
,
四边形
是平行四边形,
,,
,,
.
.
(2)
.
(3)
延长
,
交于
,连接
.
,,
四边形
为平行四边形,
,
平分
,
,,,
为等腰三角形,
,
,
平行四边形
为菱形.
,
为全等的等边三角形,
,.
,,,
,
在
与
中,
,
,
.
【解析】
(2)
连接
,.
四边形
为平行四边形,,
四边形
为矩形,
平分
,
,
,,
,,
为等腰直角三角形,
为
中点,
,,
为等腰直角三角形,,
,
,
,
在
与
中,
,
,
,
,
又
,
,
为等腰直角三角形,
.
一、选择题
如图所示,一个
角的三角形纸片,剪去这个
角后,得到一个四边形,则
的度数为
A.
B.
C.
D.
课外活动时,王老师让同学们做一个对角线互相垂直的等腰梯形形状的风筝,其面积为
,则两条对角线所用的竹条至少需
A.
B.
C.
D.
若等腰梯形两底之差等于一腰的
倍,则这个梯形的一个底角为
A.
B.
C.
D.
已知直角梯形
中,,,,,
分别是
,
边的中点,连接
,
交于点
,连接
并延长交
于点
,连接
,则下列结论不正确的是
A.
平分
B.四边形
为平行四边形
C.
将直角梯形分为面积相等的两部分
D.
为等腰三角形
如图是一块长方形的场地,长,宽,从、两处入口的中路宽都为,两小路汇合处路宽为,其余部分种植草坪,则草坪面积为
A.
B.
C.
D.
如图所示,长方形
的周长是
,以
,
为边向外作正方形
和正方形
,若正方形
和正方形
的面积之和为
,那么长方形
的面积是
A.
B.
C.
D.
正方形内有一点
,到各边的距离从小到大依次是
、
、
、
,则正方形的周长是
A.
B.
C.
D.
梯形
中
,,以
,,
为斜边向外作等腰直角三角形,其面积分别是
,,,且
,则
A.
B.
C.
D.
二、填空题
如图,
是
的中线,设向量
,,那么向量
(结果用
,
表示).
在正方形
中,
在
上,,,
是
上的动点,则
和
的长度之和最小值为
.
如图,矩形
的面积为
,它的两条对角线交于点
,以
,
为两邻边作平行四边形
,平行四边形
的对角线交于点
,同样以
,
为两邻边作平行四边形
,,依此类推,则平行四边形
的面积为
.
如图,在平行四边形
中,,
分别是边
,
的中点,
分别交
,
于点
,.给出下列结论:①
;②
;③
;④
.其中正确的结论是
(只填序号).
如图,在梯形
中,,,,,将该梯形折叠,点
恰好与点
重合,
为折痕,那么
的长度为
.
如图所示,是一块电脑屏幕上出现的矩形色块图,由
个颜色不同的正方形组成,设中间最小的一个正方形边长为
,则这个矩形的面积为
.
如图,平行四边形
中,点
在边
上,以
为折痕,将
向上翻折,点
正好落在
上的点
,若
的周长为
,
的周长为
,则
的长为
.
如图,
是矩形
内的任意一点,连接
,,,,得到
,,,,设它们的面积分别是
,,,,给出如下结论:
①
;
②
;
③若
,则
;
④若
,则
点在矩形的对角线上.
其中正确的结论的序号是
(把所有正确结论的序号都填在横线上).
三、解答题
已知:如图,在四边形
中,,,.
(1)
求证:;
(2)
当
于
时,试证明:.
如图,在梯形纸片
中,,,将纸片沿过点
的直线折叠,使点
落在
上的点
处,折痕
交
于点
,连接
.
(1)
求证:四边形
是菱形;
(2)
若
,试判断四边形
的形状,并加以证明.
探究问题:
(1)
方法感悟:
如图①,在正方形
中,点
,
分别为
,
边上的点,且满足
,连接
,求证
.
感悟解题方法,并完成下列填空:
将
绕点
顺时针旋转
得到
,此时
与
重合,
由旋转可得:,,,,
,
因此,点
,,
在同一条直线上.
,
.
,,即
.
又
,,
.
,故
.
(2)
方法迁移:
如图②,将
沿斜边翻折得到
,点
,
分别为
,
边上的点,且
.试猜想
,,
之间有何数量关系,并证明你的猜想.
在平行四边形
中,
的平分线交直线
于点
,交直线
于点
.
(1)
在图
中证明
;
(2)
若
,
是
的中点(如图
),直接写出
的度数;
(3)
若
,,,分别连接
,(如图
),求
的度数.
答案
一、选择题
1.
【答案】C
2.
【答案】C
【解析】如图.
且
,
又
等腰梯形
的面积为
,
,解得
.
3.
【答案】C
【解析】如图,,设
,则
,作过点
,
的高
,,
则四边形
为矩形,
.
等腰梯形是轴对称图形,
,
,
.
4.
【答案】C
【解析】本题可用排除法解题,由题意易证
,得
,
.
.
.
.
选项
A
正确;
且
,
四边形
为平行四边形,选项
B
正确;
,,
,即选项
D
正确.
5.
【答案】B
【解析】【分析】根据已知将道路平移,再利用矩形的性质求出长和宽,再进行解答.
【解析】解:由图可知:矩形中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:米,宽为米.
所以草坪的面积应该是长宽米.
故选:.
【点评】此题考查了生活中的平移,根据图形得出草坪正好可以拼成一个长方形是解题关键.
6.
【答案】B
【解析】设
,,则正方形
的面积为
,正方形
的面积为
,可列出方程为
,解得
,.若
,则
;若
,则
.此时长方形
的面积均为
.
7.
【答案】B
8.
【答案】B
二、填空题
9.
【答案】
【解析】
是
的中线,,
,
,
.
10.
【答案】
【解析】连接
,,
与
交于点
,
此时
的最小,即
就是
的长度.
正方形
中,,,
,
.
11.
【答案】
12.
【答案】①②③
【解析】在平行四边形
中,,,
又
,
分别是边
,
的中点,
,,
四边形
是平行四边形,
,
,
,,
;
是
的中点,,
是
的中点,
同理
是
的中点,
,
;
.不成立,
正确的结论是①②③.
13.
【答案】
【解析】过点
作
,垂足为
,
根据题意,,
,
在
中,由勾股定理得,.
14.
【答案】
【解析】设右下角的小正方形①边长为
,则②③④⑤边长分别为
,,,.矩形的长(下边),矩形的长(上边),则
,
解得
,
②③④⑤边长分别为
,,,,
矩形的长
,宽
,
面积
.
15.
【答案】
【解析】设
,,
平行四边形
,
,,
为折痕,
,,
周长为
,
的周长为
,
,,
,解得
.
16.
【答案】②④
【解析】过点
分别向
,
作垂线段,两个三角形的面积之和等于矩形面积的一半,同理,过点
分别向
,
作垂线段,两个三角形的面积之和等于矩形面积的一半.
.
又
,.
所以成立的答案是②④.
三、解答题
17.
【答案】
(1)
连接
.
,
.
,
.
,
.
.
(2)
过
作
于
.
,
四边形
是矩形.
.
,,
.
又
,,
.
.
.
18.
【答案】
(1)
依题意
,,,
,
.
.
.
故
,四边形
是菱形.
(2)
四边形
为平行四边形.
证明:
,
又
,
.
又
,
.
又
,可得
.
四边形
为平行四边形.
19.
【答案】
(1)
;;
(2)
.理由如下:
假设
的度数为
,将
绕点
顺时针旋转
得到
,如图,此时
与
重合,
由旋转可得:,,,,
,
因此,点
,,
在同一条直线上.
,
.
,
,即
.
在
和
中,
.
.
又
,
.
【解析】
(1)
如图①所示;
根据等量代换得出
,
利用
得出
,
.
20.
【答案】
(1)
如图
,
平分
,
,
四边形
是平行四边形,
,,
,,
.
.
(2)
.
(3)
延长
,
交于
,连接
.
,,
四边形
为平行四边形,
,
平分
,
,,,
为等腰三角形,
,
,
平行四边形
为菱形.
,
为全等的等边三角形,
,.
,,,
,
在
与
中,
,
,
.
【解析】
(2)
连接
,.
四边形
为平行四边形,,
四边形
为矩形,
平分
,
,
,,
,,
为等腰直角三角形,
为
中点,
,,
为等腰直角三角形,,
,
,
,
在
与
中,
,
,
,
,
又
,
,
为等腰直角三角形,
.
