六年级数学下册教案 4 比例 苏教版
文档属性
| 名称 | 六年级数学下册教案 4 比例 苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 326.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 20:32:36 | ||
图片预览

文档简介
第四单元
比例(单元复习一)
教学内容:义务教育教科书数学六年级下册第四单元《比例》单元复习。
教学目标:1、通过整理和复习,使学生在具体情境中进一步理解图形的放大与缩小,能在方格纸上将简单图形放大或缩小。
2、通过复习,联系图形的放大与缩小理解比例的意义,进一步认识比例的项和内项、外项;在复习中进一步掌握比例的基本性质,能应用比例的基本性质解比例。
3、通过复习,使学生经历认识比例和应用比例的有关知识解决问题的过程,进一步丰富对现实世界中数量关系的认识,体会不同部分数学知识之间的联系,获得一些解决问题的策略,培养初步的形象思维和逻辑思维能力,发展空间观念。
教学重点:进一步理解图形的放大与缩小;理解并掌握比例的意义和基本性质,会解比例。
教学难点:在方格纸上按指定的比将简单图形放大或缩小。应用比例的基本性质解决实际问题。
教学准备:课件,方格纸。
教学过程:
一、回顾本单元知识
师:这节课我们一起复习第四单元-------比例。首先回顾一下,本单元我们学习了哪些知识?(板书课题)
生:图形的放大与缩小、比例的意义、比例的基本性质、解比例、比例尺。
二、复习图形的放大与缩小
1、师:已知这两幅图的长和宽,想一想,第二幅图是按几比几放大的?
师:2:1是什么意思?生:现在的长与原来长的比是2:1,现在的宽与原来宽的比是2:1。
根据学生的回答板书:2
:
1
现在
:
原来
师:放大或缩小后的图形与原来图形相比,什么变了,什么没变。
师:根据对应边的长度比就能判断图形是放大还是缩小。
2、练习。(抢答)
下面的这些比哪些表示把图形放大,哪些表示把图形缩小?
4:1
1:1000
5:2
2:3
1:1
100:1
学生抢答,并说说判断的依据。
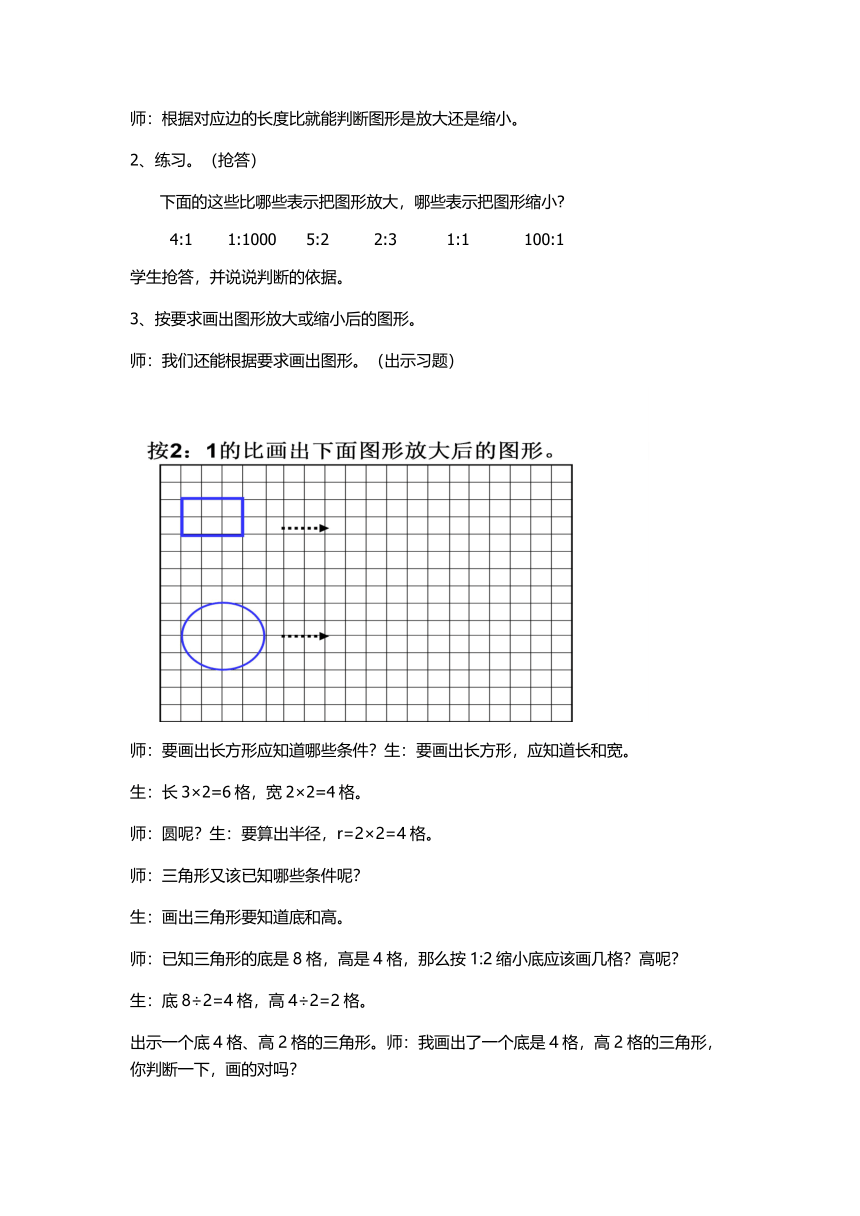
3、按要求画出图形放大或缩小后的图形。
师:我们还能根据要求画出图形。(出示习题)
师:要画出长方形应知道哪些条件?生:要画出长方形,应知道长和宽。
生:长3×2=6格,宽2×2=4格。
师:圆呢?生:要算出半径,r=2×2=4格。
师:三角形又该已知哪些条件呢?
生:画出三角形要知道底和高。
师:已知三角形的底是8格,高是4格,那么按1:2缩小底应该画几格?高呢?
生:底8÷2=4格,高4÷2=2格。
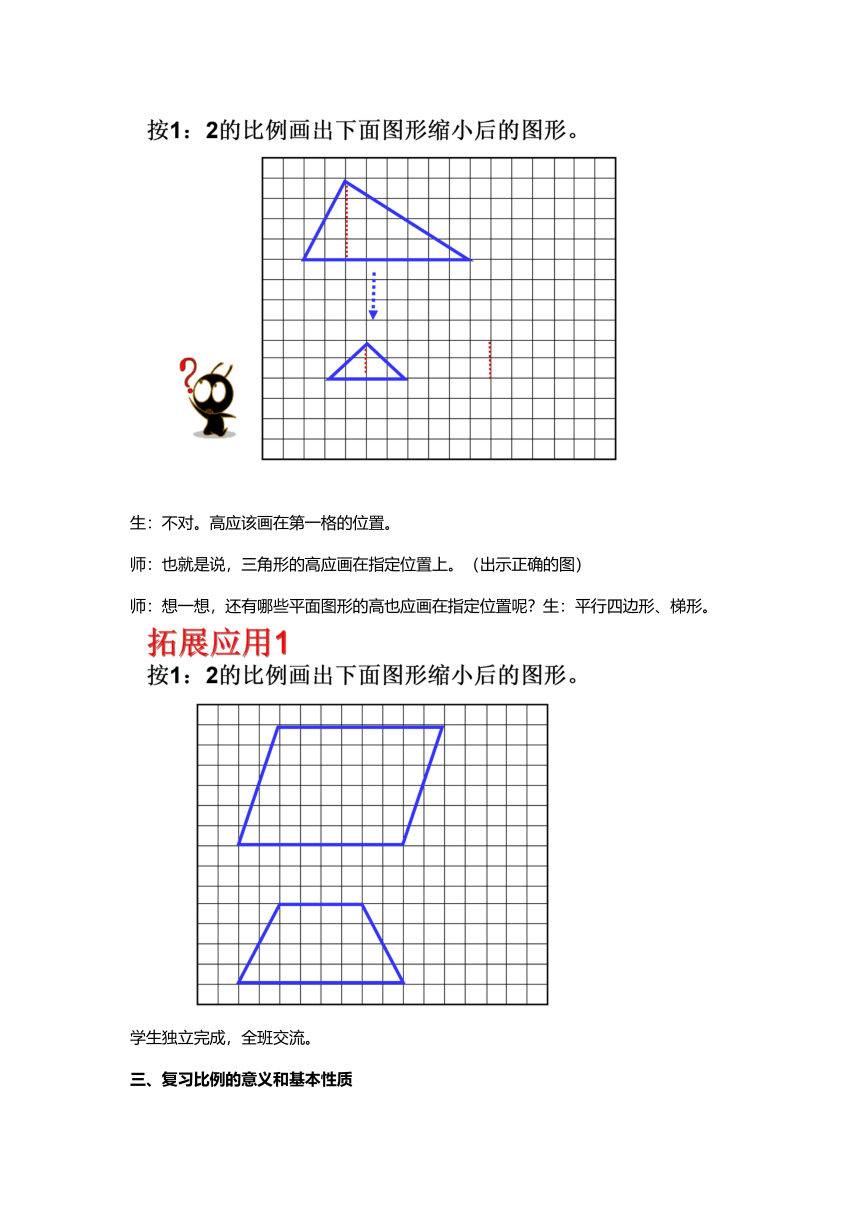
出示一个底4格、高2格的三角形。师:我画出了一个底是4格,高2格的三角形,你判断一下,画的对吗?
生:不对。高应该画在第一格的位置。
师:也就是说,三角形的高应画在指定位置上。(出示正确的图)
师:想一想,还有哪些平面图形的高也应画在指定位置呢?生:平行四边形、梯形。
学生独立完成,全班交流。
三、复习比例的意义和基本性质
1、我们认识了比例,想一想,什么叫比例?
生:表示两个比相等的式子叫比例。
师:这里的6.4:4是一个比,6.4:4=9.6:6是一个比例,那么比和比例有什么区别呢?
学生自由交流。
生:两个数相除,又叫两个数的比。表示两个比相等的式子,叫做比例。
生:比有两个项,比例有四个项。
生:比是一个比,比例是一个等式。
2、根据比例的意义可以判断两个比能否组成比例。
出示练习:根据比例的意义,判断下面哪组中的两个比可以组成比例(口答)。
6∶5
和
12∶10
5∶1
和
6∶2
3、师:还可以根据比例的基本性质来判断,那么什么叫比例的基本性质?
生:在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
师:如果用字母表示比例的四个项,那么这个规律可以表示成------
生:ad=bc
板书:a:b=c:d,那么ad=bc
4、练习:(1)
根据比例的基本性质,将下列各比例改写成乘法等式(口答)。
3∶8
=
15∶40
9/1.6=4.5/0.8
生口答:3×40=8×15
9×0.8=1.6×4.5
(2)师:应用比例的基本性质,可以判断两个比能否组成比例。。
出示:6:5和12:10
5:2和8:5
学生依次口答。
(3)出示练习:哪一组中的四个数可以组成比例?把组成的比例写出来。
(1)6、4、18和12
(2)4、5、6和8
(4)拓展:①a×4=b×7,那么b:a=(
):(
)
师:你是怎样想的?
②a+b=80,a÷b=2/3,那么b=(
)
四、复习解比例。
1、根据比例的基本性质可以解比例。什么叫解比例?
生:求比例中的未知项,叫解比例。
出示例题:解比例9/x=4.5/0.8
2、练习:解比例。
2:8=9:x
x/25=1.2/75
分组练习,集体校对。
3、解决问题。
(1)平面图形中的问题
看图求出未知数x的值。
(2)立体图形中的问题
两个圆柱的底面积相等,第一个圆柱与第二个圆柱高的比是7:11,第二个圆柱的体积是132立方分米,第一个圆柱的体积是多少?
(3)生活中的问题
法国巴黎的埃菲尔铁塔高320米,北京的“世界公园”里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是1:10。这座模型高多少米?
五、课时小结。这节课你又有了哪些收获?
六、思考:5、4、8和另一个数可以组成比例,这个数可能是多少?
比例(单元复习一)
教学内容:义务教育教科书数学六年级下册第四单元《比例》单元复习。
教学目标:1、通过整理和复习,使学生在具体情境中进一步理解图形的放大与缩小,能在方格纸上将简单图形放大或缩小。
2、通过复习,联系图形的放大与缩小理解比例的意义,进一步认识比例的项和内项、外项;在复习中进一步掌握比例的基本性质,能应用比例的基本性质解比例。
3、通过复习,使学生经历认识比例和应用比例的有关知识解决问题的过程,进一步丰富对现实世界中数量关系的认识,体会不同部分数学知识之间的联系,获得一些解决问题的策略,培养初步的形象思维和逻辑思维能力,发展空间观念。
教学重点:进一步理解图形的放大与缩小;理解并掌握比例的意义和基本性质,会解比例。
教学难点:在方格纸上按指定的比将简单图形放大或缩小。应用比例的基本性质解决实际问题。
教学准备:课件,方格纸。
教学过程:
一、回顾本单元知识
师:这节课我们一起复习第四单元-------比例。首先回顾一下,本单元我们学习了哪些知识?(板书课题)
生:图形的放大与缩小、比例的意义、比例的基本性质、解比例、比例尺。
二、复习图形的放大与缩小
1、师:已知这两幅图的长和宽,想一想,第二幅图是按几比几放大的?
师:2:1是什么意思?生:现在的长与原来长的比是2:1,现在的宽与原来宽的比是2:1。
根据学生的回答板书:2
:
1
现在
:
原来
师:放大或缩小后的图形与原来图形相比,什么变了,什么没变。
师:根据对应边的长度比就能判断图形是放大还是缩小。
2、练习。(抢答)
下面的这些比哪些表示把图形放大,哪些表示把图形缩小?
4:1
1:1000
5:2
2:3
1:1
100:1
学生抢答,并说说判断的依据。
3、按要求画出图形放大或缩小后的图形。
师:我们还能根据要求画出图形。(出示习题)
师:要画出长方形应知道哪些条件?生:要画出长方形,应知道长和宽。
生:长3×2=6格,宽2×2=4格。
师:圆呢?生:要算出半径,r=2×2=4格。
师:三角形又该已知哪些条件呢?
生:画出三角形要知道底和高。
师:已知三角形的底是8格,高是4格,那么按1:2缩小底应该画几格?高呢?
生:底8÷2=4格,高4÷2=2格。
出示一个底4格、高2格的三角形。师:我画出了一个底是4格,高2格的三角形,你判断一下,画的对吗?
生:不对。高应该画在第一格的位置。
师:也就是说,三角形的高应画在指定位置上。(出示正确的图)
师:想一想,还有哪些平面图形的高也应画在指定位置呢?生:平行四边形、梯形。
学生独立完成,全班交流。
三、复习比例的意义和基本性质
1、我们认识了比例,想一想,什么叫比例?
生:表示两个比相等的式子叫比例。
师:这里的6.4:4是一个比,6.4:4=9.6:6是一个比例,那么比和比例有什么区别呢?
学生自由交流。
生:两个数相除,又叫两个数的比。表示两个比相等的式子,叫做比例。
生:比有两个项,比例有四个项。
生:比是一个比,比例是一个等式。
2、根据比例的意义可以判断两个比能否组成比例。
出示练习:根据比例的意义,判断下面哪组中的两个比可以组成比例(口答)。
6∶5
和
12∶10
5∶1
和
6∶2
3、师:还可以根据比例的基本性质来判断,那么什么叫比例的基本性质?
生:在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
师:如果用字母表示比例的四个项,那么这个规律可以表示成------
生:ad=bc
板书:a:b=c:d,那么ad=bc
4、练习:(1)
根据比例的基本性质,将下列各比例改写成乘法等式(口答)。
3∶8
=
15∶40
9/1.6=4.5/0.8
生口答:3×40=8×15
9×0.8=1.6×4.5
(2)师:应用比例的基本性质,可以判断两个比能否组成比例。。
出示:6:5和12:10
5:2和8:5
学生依次口答。
(3)出示练习:哪一组中的四个数可以组成比例?把组成的比例写出来。
(1)6、4、18和12
(2)4、5、6和8
(4)拓展:①a×4=b×7,那么b:a=(
):(
)
师:你是怎样想的?
②a+b=80,a÷b=2/3,那么b=(
)
四、复习解比例。
1、根据比例的基本性质可以解比例。什么叫解比例?
生:求比例中的未知项,叫解比例。
出示例题:解比例9/x=4.5/0.8
2、练习:解比例。
2:8=9:x
x/25=1.2/75
分组练习,集体校对。
3、解决问题。
(1)平面图形中的问题
看图求出未知数x的值。
(2)立体图形中的问题
两个圆柱的底面积相等,第一个圆柱与第二个圆柱高的比是7:11,第二个圆柱的体积是132立方分米,第一个圆柱的体积是多少?
(3)生活中的问题
法国巴黎的埃菲尔铁塔高320米,北京的“世界公园”里有一座埃菲尔铁塔的模型,它的高度与原塔高度的比是1:10。这座模型高多少米?
五、课时小结。这节课你又有了哪些收获?
六、思考:5、4、8和另一个数可以组成比例,这个数可能是多少?
