五年级数学下册课件-7 解决问题的策略—转化-苏教版(33张PPT)
文档属性
| 名称 | 五年级数学下册课件-7 解决问题的策略—转化-苏教版(33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 10:24:31 | ||
图片预览





文档简介
解决问题的策略—转化
苏教版五年级数学下册
大象
石头
转化
同等重量
操作要求:
1.每组组长负责拿剪刀操作。
2. 其他同学要仔细观察,讨论交流,完成学习单。
3.副组长负责检查学习单的完成情况。
4.操作时间是5分钟。
5.操作过程中一定要注意安全!
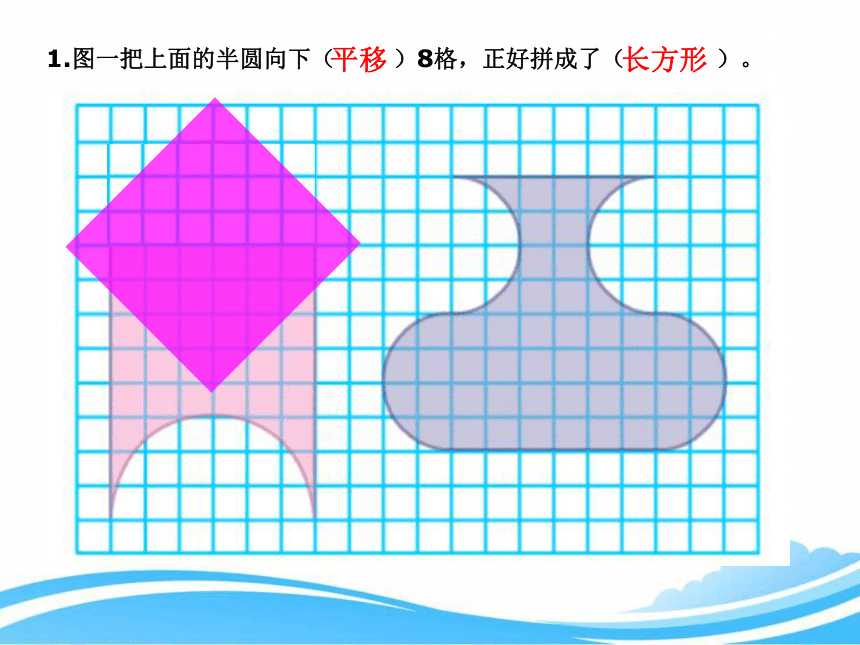
将上面的半圆 向下平移8格
1.图一把上面的半圆向下( )8格,正好拼成了( )。
平移
长方形
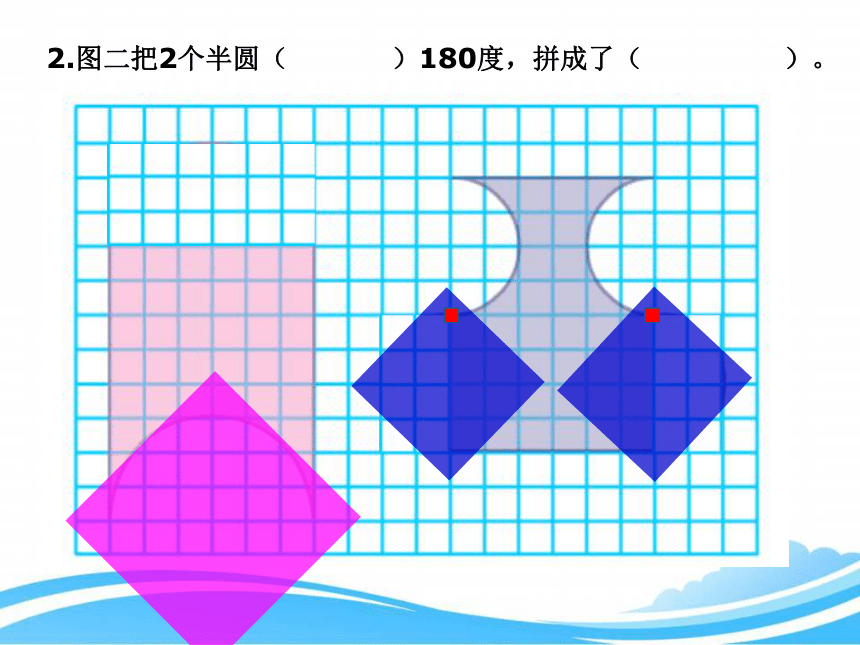
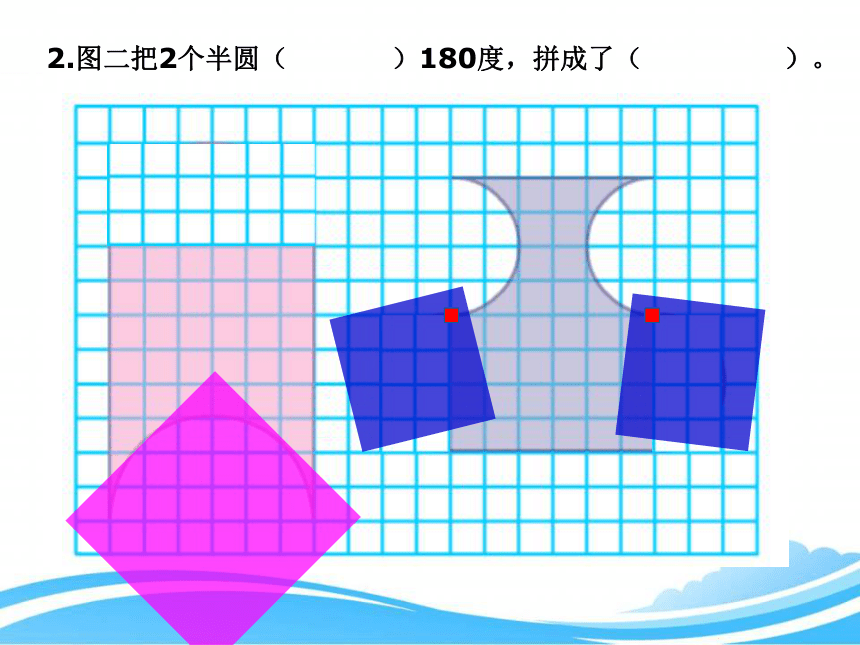
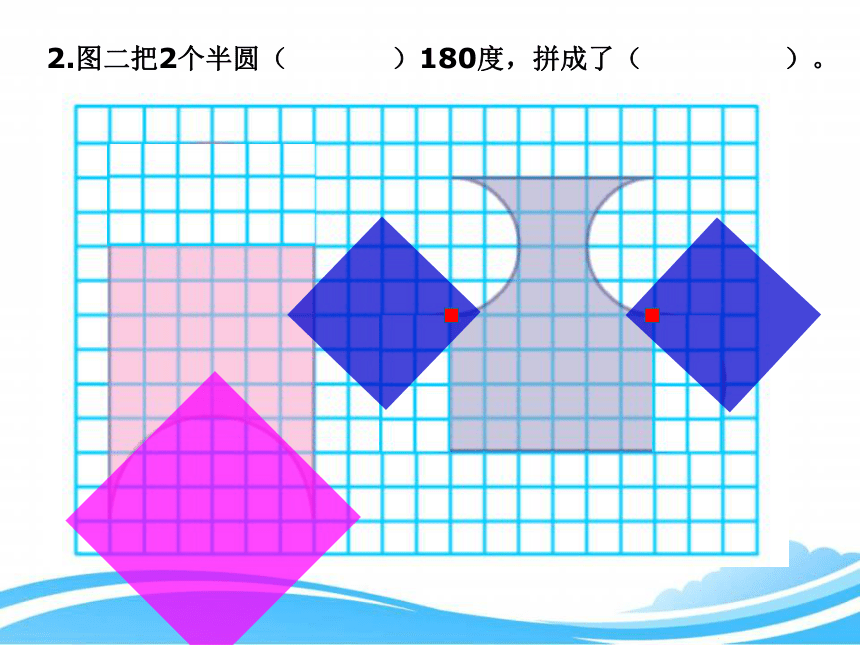
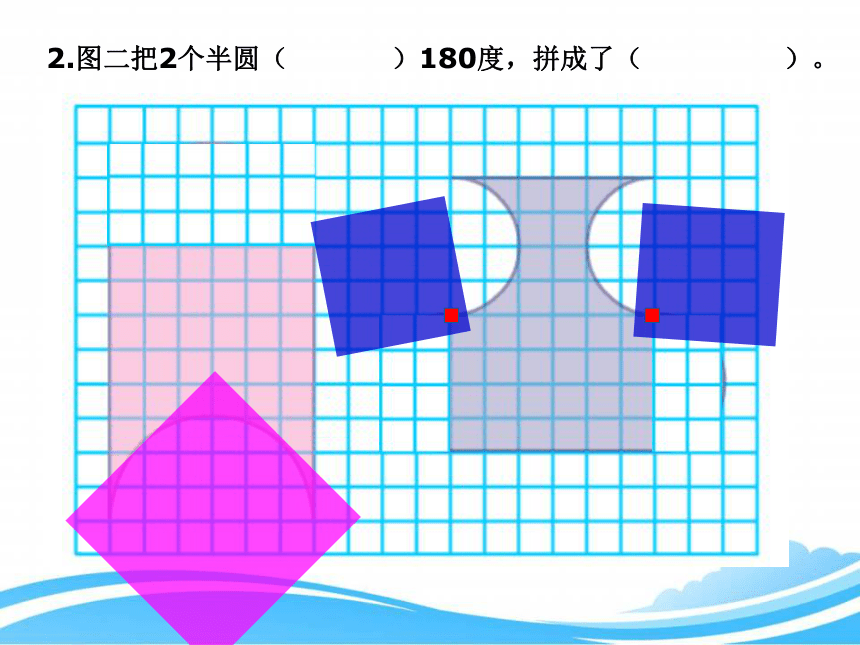
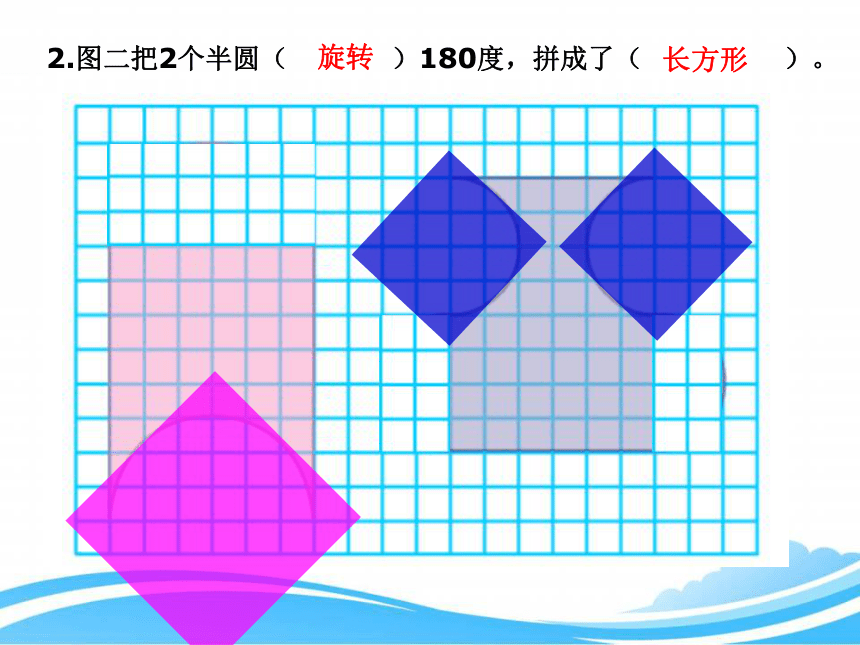
2.图二把2个半圆( )180度,拼成了( )。
2.图二把2个半圆( )180度,拼成了( )。
2.图二把2个半圆( )180度,拼成了( )。
2.图二把2个半圆( )180度,拼成了( )。
2.图二把2个半圆( )180度,拼成了( )。
旋转
长方形
2.图二把2个半圆( )180度,拼成了( )。
3.比较这两个图形的大小,我发现它们面积( )。
相等
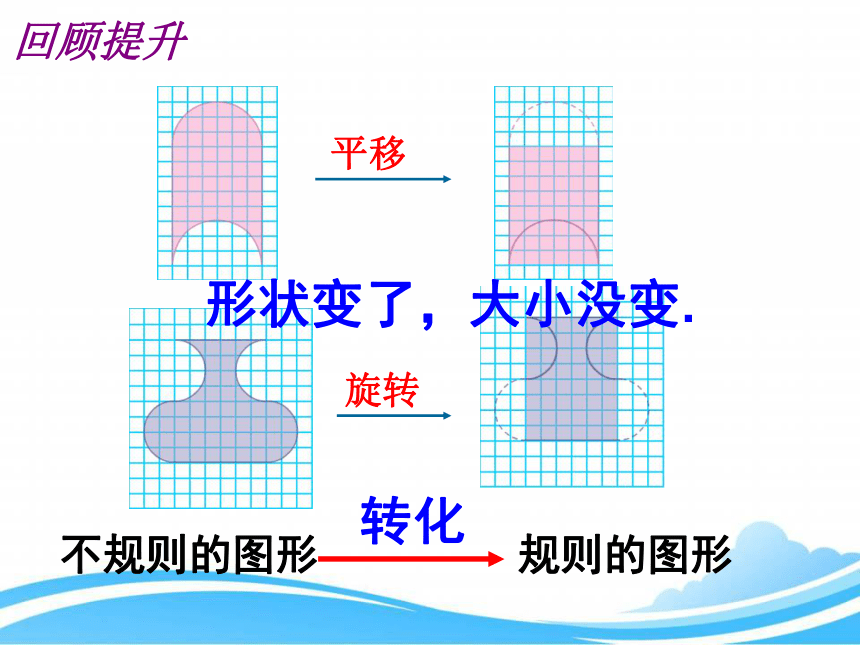
不规则的图形
规则的图形
转化
回顾提升
形状变了,大小没变.
平移
旋转
1.解决例1提出的问题,我们应用了什么策略?
平移,旋转
2.用什么方法把不规则图形转化成规则图形?
转化
3.转化后的图形和转化前比,什么变了?什么不变?
形状变了,大小不变
这两个图案的面积相等。
2.观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm?
(5+3)×2=16cm
2.用分数表示图中的涂色部分。
( )
( )
1
4
2.用分数表示图中的涂色部分。
( )
( )
1
4
2.用分数表示图中的涂色部分。
( )
( )
1
2
2.用分数表示图中的涂色部分。
( )
( )
1
2
2.用分数表示图中的涂色部分。
( )
( )
5
8
2.用分数表示图中的涂色部分。
以前的学习中,哪些地方也用到了转化的策略?
推导平行四边形的面积公式。
推导三角形的面积公式.
推导梯形的面积公式
小数乘法可以先转化成整数计算
“图形”的转化
计算中“数”的转化
通过刚才的学习和回顾,你认为转化有哪些好处?
(化繁为简、化难为易、化陌生的新知为熟悉的旧知)
化曲为直
化繁为简
苏教版五年级数学下册
大象
石头
转化
同等重量
操作要求:
1.每组组长负责拿剪刀操作。
2. 其他同学要仔细观察,讨论交流,完成学习单。
3.副组长负责检查学习单的完成情况。
4.操作时间是5分钟。
5.操作过程中一定要注意安全!
将上面的半圆 向下平移8格
1.图一把上面的半圆向下( )8格,正好拼成了( )。
平移
长方形
2.图二把2个半圆( )180度,拼成了( )。
2.图二把2个半圆( )180度,拼成了( )。
2.图二把2个半圆( )180度,拼成了( )。
2.图二把2个半圆( )180度,拼成了( )。
2.图二把2个半圆( )180度,拼成了( )。
旋转
长方形
2.图二把2个半圆( )180度,拼成了( )。
3.比较这两个图形的大小,我发现它们面积( )。
相等
不规则的图形
规则的图形
转化
回顾提升
形状变了,大小没变.
平移
旋转
1.解决例1提出的问题,我们应用了什么策略?
平移,旋转
2.用什么方法把不规则图形转化成规则图形?
转化
3.转化后的图形和转化前比,什么变了?什么不变?
形状变了,大小不变
这两个图案的面积相等。
2.观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便?
每个小方格的边长是1cm,右边图形的周长是多少cm?
(5+3)×2=16cm
2.用分数表示图中的涂色部分。
( )
( )
1
4
2.用分数表示图中的涂色部分。
( )
( )
1
4
2.用分数表示图中的涂色部分。
( )
( )
1
2
2.用分数表示图中的涂色部分。
( )
( )
1
2
2.用分数表示图中的涂色部分。
( )
( )
5
8
2.用分数表示图中的涂色部分。
以前的学习中,哪些地方也用到了转化的策略?
推导平行四边形的面积公式。
推导三角形的面积公式.
推导梯形的面积公式
小数乘法可以先转化成整数计算
“图形”的转化
计算中“数”的转化
通过刚才的学习和回顾,你认为转化有哪些好处?
(化繁为简、化难为易、化陌生的新知为熟悉的旧知)
化曲为直
化繁为简
