《圆与圆的位置关系》学案
图片预览
文档简介
总 课 题 圆与方程 总课时
分 课 题 圆与圆的位置关系 分课时
教学目标 掌握圆心距和半径的大小关系;判断圆和圆的位置关系.
重点难点 根据两圆的方程判断两圆的位置关系,会求相交两圆的公共弦所在直线方程及弦长.
引入新课
圆与圆有哪些位置关系?怎样进行判断呢?需要哪些步骤呢?
第一步:
第二步:
第三步:
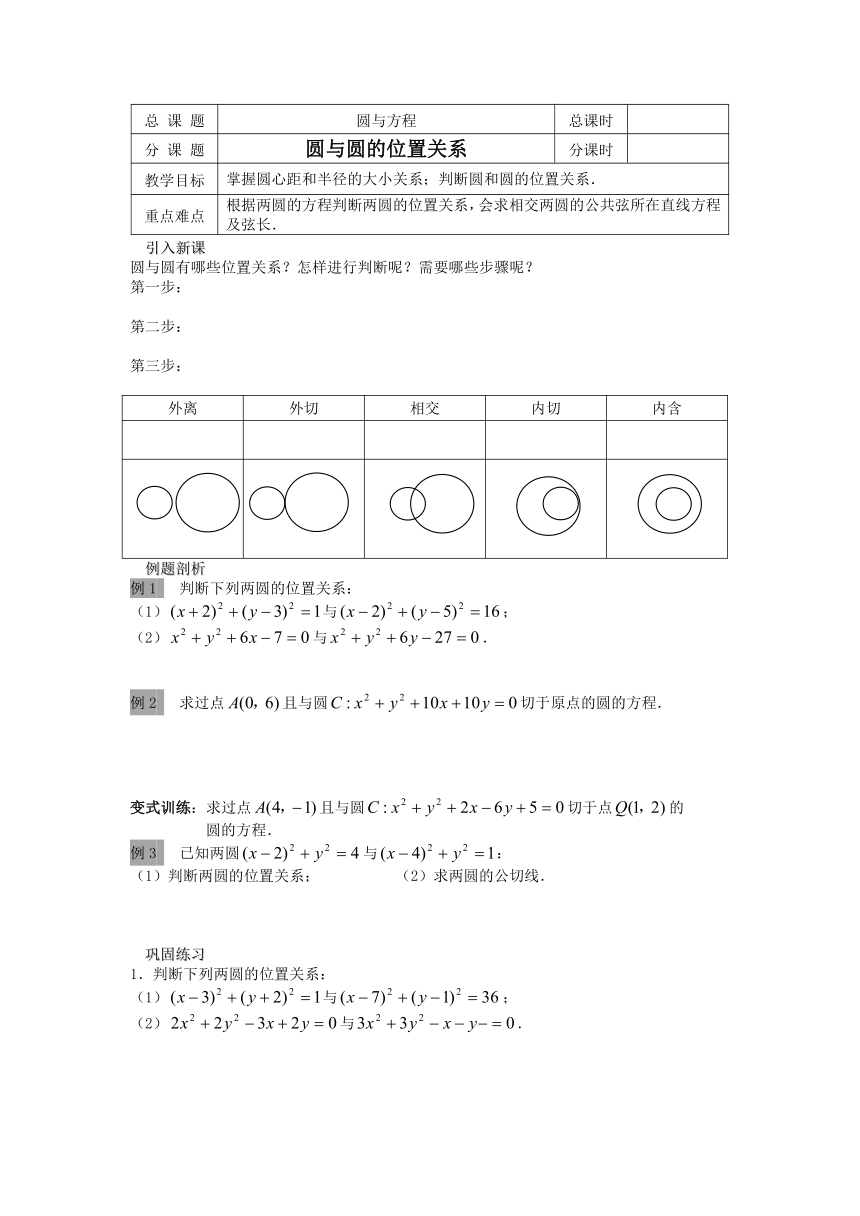
外离 外切 相交 内切 内含
例题剖析
例1 判断下列两圆的位置关系:
(1)与;
(2)与.
例2 求过点且与圆切于原点的圆的方程.
变式训练:求过点且与圆切于点的
圆的方程.
例3 已知两圆与:
(1)判断两圆的位置关系; (2)求两圆的公切线.
巩固练习
1.判断下列两圆的位置关系:
(1)与;
(2)与.
2.已知圆与圆相交,求实数的取值范围.
3.已知以为圆心的圆与圆相切,求圆的方程.
4.已知一圆经过直线与圆的两个
交点,并且有最小面积,求此圆的方程.
课堂小结
利用圆心距和半径的大小关系判断圆和圆的位置关系.根据两圆的方程判断两圆的位置关系,会求相交两圆是公共弦所在的直线方程及弦长.
课后训练
一 基础题
1.圆与圆的位置关
系是 .
2.圆和与圆的交点坐标为 .
3.圆与圆的公共弦所在直线方
程为 .
4.已知动圆恒过定点,则点的坐标是 .
二 提高题
5.求圆心在直线上,且经过圆与圆
交点的圆的方程.
6.求圆与圆的公共弦所在
直线方程.
三 能力题
7.已知一圆经过圆与圆的两个交
点,且圆心在直线上,求该圆的方程.
www.
分 课 题 圆与圆的位置关系 分课时
教学目标 掌握圆心距和半径的大小关系;判断圆和圆的位置关系.
重点难点 根据两圆的方程判断两圆的位置关系,会求相交两圆的公共弦所在直线方程及弦长.
引入新课
圆与圆有哪些位置关系?怎样进行判断呢?需要哪些步骤呢?
第一步:
第二步:
第三步:
外离 外切 相交 内切 内含
例题剖析
例1 判断下列两圆的位置关系:
(1)与;
(2)与.
例2 求过点且与圆切于原点的圆的方程.
变式训练:求过点且与圆切于点的
圆的方程.
例3 已知两圆与:
(1)判断两圆的位置关系; (2)求两圆的公切线.
巩固练习
1.判断下列两圆的位置关系:
(1)与;
(2)与.
2.已知圆与圆相交,求实数的取值范围.
3.已知以为圆心的圆与圆相切,求圆的方程.
4.已知一圆经过直线与圆的两个
交点,并且有最小面积,求此圆的方程.
课堂小结
利用圆心距和半径的大小关系判断圆和圆的位置关系.根据两圆的方程判断两圆的位置关系,会求相交两圆是公共弦所在的直线方程及弦长.
课后训练
一 基础题
1.圆与圆的位置关
系是 .
2.圆和与圆的交点坐标为 .
3.圆与圆的公共弦所在直线方
程为 .
4.已知动圆恒过定点,则点的坐标是 .
二 提高题
5.求圆心在直线上,且经过圆与圆
交点的圆的方程.
6.求圆与圆的公共弦所在
直线方程.
三 能力题
7.已知一圆经过圆与圆的两个交
点,且圆心在直线上,求该圆的方程.
www.
