2020-2021学年七年级数学人教版下册 第七章 7.1.1 有序数对 课件(共59张PPT)
文档属性
| 名称 | 2020-2021学年七年级数学人教版下册 第七章 7.1.1 有序数对 课件(共59张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 20:30:38 | ||
图片预览










文档简介
(共59张PPT)
第七章
7.1.1
有序数对
人教版数学七年级下册
1.通过丰富的实例认识有序数对,感受它在确定点的位置中的作用.
2.了解有序数对的概念,学会用有序数刘表示点的位置.
学习目标
在数轴上,确定一个点的位置需要几个数据呢?
答:一个,例如:
若A点表示-2,B点表示3,则由-2和3就可以在
数轴上找到A点和B点的位置.
在直线上,确定一个点的位置一般需要一个数据.
0
1
2
3
-2
-1
复习导入
1
知识点
确定位置的条件
问题(1):在班里老师有一位朋友,你知道是谁吗?
问题(2):你认为确定你朋友的位置需要几个数据?
合作探究
议一议
(1)在电影院内,确定一个座位一般需要几个
数据?
(2)在生活中,确定物体的位置还有其他方法
吗?与同伴进行交流.
(3)在平面内,确定一个点的位置一般需要几
个数据呢?
下列数据,不能确定物体位置的是(
)
A.4号楼
B.新华路25号
C.北偏东25°
D.东经118°,北纬45°
例1
解:北偏东25°只能确定方向,不能确定位置.
故选C.
C
1
一般来说,要确定平面内一个物体的位置,需要
________个数据.
2
有人在市中心打听一中的位置,问了三个人,得
到三种不同的回答:
①在市中心的西北方向;
②距市中心1
km;
③在市中心的西北方向,距市中心1
km处.
在上述回答中能确定一中位置的是______.(填序号)
两
③
巩固新知
3
下列说法能确定台风位置的是( )
A.西太平洋
B.北纬28°,东经135°
C.距离台湾300海里
D.台湾与冲绳之间
B
2
知识点
有序数对
我们都有去影剧院看电影的经历.
你一定知道,影剧院对观众席的
所有座位都按“几排几号”编号,
以便确定每一个座位在影剧院中
的位置.这样,观众就能根据入场
券上的“排数”和“号数”准确
地“对号入座”.
合作探究
这种办法在日常生活中是常用的.
比如,当发现一本
书上某页有一处印刷错误时,你可以怎样告诉其他
同学这一处的位置呢?又如,假设根据教室平面图
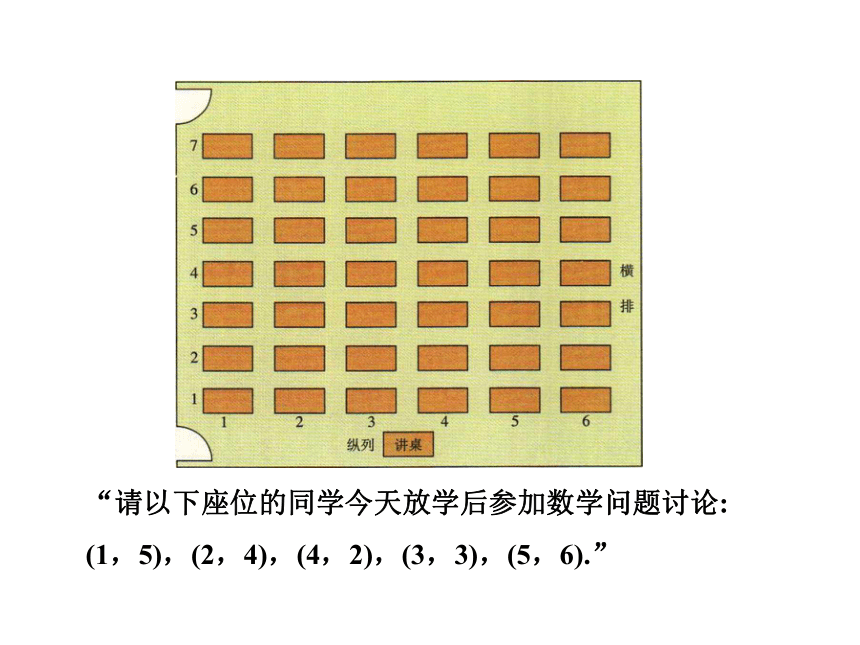
(下图)写出如下通知,你知道哪些同学参加讨论吗?
“请以下座位的同学今天放学后参加数学问题讨论:
(1,5),(2,4),(4,2),(3,3),(5,6).”
思考
怎样确定教室里座位的位置?排数和列数的先后顺
序对位置有影响吗?假设我们约定“列数在前,排
数在后”,请你在图上标出被邀请参加讨论的同学
的座位.
上面的问题都是通过像“9排7号”“第1列第5排”
这样含有两个数的表达方式来表示一个确定的位置,
其中两个数各自表示不同的含义,例如前边的表示
“排数”,后边的表示“号数”.
我们把这种有顺序
的两个数a与b组成的数对,叫做有序数对,记作(a,b).
新知小结
如图是某教室学生座位的平面图.
(1)请说出王明和陈帅的座位位置;
(2)若用(3,2)表示第3排第2列的位置,那么(5,5)
表示什么位置?王明和陈帅的座位位置可以怎
样表示?
例2
合作探究
(3)请说出(3,3)和(4,8)分别表示哪两位同学的座位
位置;
(4)(2,3)和(3,2)表示的位置相同吗?一般地,若
a≠b,(a,b)与(b,a)表示的位置相同吗?
导引:
平面上确定物体的位置有多种方法,但基本上
都需要两个数据,本例可以通过排数和列数来
确定位置,即先确定有序数对的第一个数,再
确定第二个数.
解:
(1)王明的座位位置是第1排第2列;陈帅的座位位置是
第5排第4列.
(2)(5,5)表示的位置是第5排第5列;王明的座位位置可
表示为(1,2),陈帅的座位位置可表示为(5,4).
(3)
(3,3)表示张军的座位位置;(4,8)表示夏凡的座位
位置.
(4)
(2,3)表示的是第2排第3列的位置,(3,2)表示的是
第3排第2列的位置,所以它们表示的位置不相同.
一般地,若a≠b,(a,b)与(b,a)表示的位置不相同.
用有序数对来描述物体(点)的位置,其中“有序”
是指(a,b)(a≠b)与(b,a)中a与b的前后顺序不同,描述
的位置就不同,如例题中的(3,4)和(4,3)表示不同的
两个位置;“数对”是指必须有两个数才能确定某点
的位置.
新知小结
1
用x和y组成一个有序数对,可以写成( )
A.(x,y)
B.(y,x)
C.
x,y或y,x
D.(x,y)或(y,x)
D
巩固新知
2
一个有序数对可以( )
A.确定一个点的位置
B.确定两个点的位置
C.确定一个或两个点的位置
D.不能确定点的位置
A
3
下列关于有序数对的说法正确的是( )
A.(2,3)与(3,2)表示的位置相同
B.(m,n)与(n,m)表示的位置一定不同
C.(2,-3)与(-3,2)是表示不同位置的两个有
序数对
D.(-1,-1)与(-1,-1)不是同一位置的点
C
3
知识点
用有序数对表示位置
用有序实数对确定位置:
定义:有顺序的两个数a与b组成的数对,叫做有
序数对,记作(a,b).
作用:平面上每一个点都对应着一个有序数对,
每一个有序数对都对应着一个点,因此,利用有
序数对可以准确地描述物体的位置,
即:平面上的点?有序数对.
合作探究
座位问题:
讲台
1
2
3
4
5
6
7
横排
1
2
3
4
5
6
若我们约定“列数在前,排数在后”.
请在教室找到如下表用数对表示的同学位置.
数对
(1,3)
(3,1)
(2,4)
(4,2)
(3,6)
(6,3)
约定:
列数在前
排数在后
温馨提示
数对是有顺序的!
[中考·盐城]如图,已知棋子“卒”表示为(-2,3),棋子“马”表示为(1,3),则棋子“炮”表示为________.
例3
先由“卒”(-2,3),“马”(1,3)确定“行”“列”序号,再写出“炮”的有序数对.
答案:(3,2)
导引:
(3,2)
利用行、列定位法确定点的位置时,首先确定平面内行、列的序号,然后写出表示平面上点的位置的有序数对.
新知小结
1
如图,甲处表示2街与5巷的十字路口,乙处表示5街与2巷的十字路口.
如果用(2,5)表示甲处的位置,那么“(2,
5)
→
(3,5)→(4,5)→(5,5)→(5,
4)
→(5,
3)→(5,
2)”表示从甲处到乙处的一种路线.
请你用这种形式
写出几种从甲处到乙处的路线.
巩固新知
答案不唯一,
如:(2,5)→(2,4)→(2,3)→(2,2)→(3,2)→(4,2)→(5,2);
(2,5)→(2,4)→(3,4)→(3,3)→(4,3)→(4,2)→(5,2).
解:
2
观察中国象棋的棋盘(如图),其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进4”后到达B
点,则表示B点位置
的数对是________.
(4,7)
3
小明坐在第5行第6列,简记为(5,6),小刚坐在第7行第4列,应记为( )
A.(7,4)
B.(4,7)
C.(7,5)
D.(7,6)
A
4
如图所示,小亮从学校到家所走最短路线是( )
(3,2)→(3,1)→(0,1)
B.(2,2)→(2,1)→(1,1)→(0,1)
C.(2,2)→(2,3)→(0,3)→(0,1)
D.(2,2)→(2,0)→(0,0)→(0,1)
B
确定平面内物体位置的方法有:
(1)行列定位法;
(2)极坐标定位法;
(3)经纬度定位法;
(4)区域定位法;
(5)网格定位法.
1
知识小结
归纳新知
不管采用哪种定位法,平面内确定位置都需要两个数据,特别是用一对数表示位置时,应注意这对数是有顺序的,顺序不同表示的位置不同.
如图是小岗在镜子中看到的自己的脸,他对妹妹说:如果我用有序数对(0,2)表示左眼,用有序数对(2,2)表示右眼,那么嘴的位置可以表示成( )
A.(1,2)
B.(2,1)
C.(1,0)
D.(0,1)
易错点:不能根据题目信息正确确定参照点
2
易错小结
C
根据小岗表示两眼的方法可知,参照点的位置在如图的O点,因此嘴的位置可
以表示成(1,0).本题易错之处
在于不能正确确定参照点.
两
课后练习
D
有序数对
a,b
D
C
括号
逗号
(3,2),
(5,7)(答案不唯一)
C
C
C
【答案】B
(3,240°)
再见
第七章
7.1.1
有序数对
人教版数学七年级下册
1.通过丰富的实例认识有序数对,感受它在确定点的位置中的作用.
2.了解有序数对的概念,学会用有序数刘表示点的位置.
学习目标
在数轴上,确定一个点的位置需要几个数据呢?
答:一个,例如:
若A点表示-2,B点表示3,则由-2和3就可以在
数轴上找到A点和B点的位置.
在直线上,确定一个点的位置一般需要一个数据.
0
1
2
3
-2
-1
复习导入
1
知识点
确定位置的条件
问题(1):在班里老师有一位朋友,你知道是谁吗?
问题(2):你认为确定你朋友的位置需要几个数据?
合作探究
议一议
(1)在电影院内,确定一个座位一般需要几个
数据?
(2)在生活中,确定物体的位置还有其他方法
吗?与同伴进行交流.
(3)在平面内,确定一个点的位置一般需要几
个数据呢?
下列数据,不能确定物体位置的是(
)
A.4号楼
B.新华路25号
C.北偏东25°
D.东经118°,北纬45°
例1
解:北偏东25°只能确定方向,不能确定位置.
故选C.
C
1
一般来说,要确定平面内一个物体的位置,需要
________个数据.
2
有人在市中心打听一中的位置,问了三个人,得
到三种不同的回答:
①在市中心的西北方向;
②距市中心1
km;
③在市中心的西北方向,距市中心1
km处.
在上述回答中能确定一中位置的是______.(填序号)
两
③
巩固新知
3
下列说法能确定台风位置的是( )
A.西太平洋
B.北纬28°,东经135°
C.距离台湾300海里
D.台湾与冲绳之间
B
2
知识点
有序数对
我们都有去影剧院看电影的经历.
你一定知道,影剧院对观众席的
所有座位都按“几排几号”编号,
以便确定每一个座位在影剧院中
的位置.这样,观众就能根据入场
券上的“排数”和“号数”准确
地“对号入座”.
合作探究
这种办法在日常生活中是常用的.
比如,当发现一本
书上某页有一处印刷错误时,你可以怎样告诉其他
同学这一处的位置呢?又如,假设根据教室平面图
(下图)写出如下通知,你知道哪些同学参加讨论吗?
“请以下座位的同学今天放学后参加数学问题讨论:
(1,5),(2,4),(4,2),(3,3),(5,6).”
思考
怎样确定教室里座位的位置?排数和列数的先后顺
序对位置有影响吗?假设我们约定“列数在前,排
数在后”,请你在图上标出被邀请参加讨论的同学
的座位.
上面的问题都是通过像“9排7号”“第1列第5排”
这样含有两个数的表达方式来表示一个确定的位置,
其中两个数各自表示不同的含义,例如前边的表示
“排数”,后边的表示“号数”.
我们把这种有顺序
的两个数a与b组成的数对,叫做有序数对,记作(a,b).
新知小结
如图是某教室学生座位的平面图.
(1)请说出王明和陈帅的座位位置;
(2)若用(3,2)表示第3排第2列的位置,那么(5,5)
表示什么位置?王明和陈帅的座位位置可以怎
样表示?
例2
合作探究
(3)请说出(3,3)和(4,8)分别表示哪两位同学的座位
位置;
(4)(2,3)和(3,2)表示的位置相同吗?一般地,若
a≠b,(a,b)与(b,a)表示的位置相同吗?
导引:
平面上确定物体的位置有多种方法,但基本上
都需要两个数据,本例可以通过排数和列数来
确定位置,即先确定有序数对的第一个数,再
确定第二个数.
解:
(1)王明的座位位置是第1排第2列;陈帅的座位位置是
第5排第4列.
(2)(5,5)表示的位置是第5排第5列;王明的座位位置可
表示为(1,2),陈帅的座位位置可表示为(5,4).
(3)
(3,3)表示张军的座位位置;(4,8)表示夏凡的座位
位置.
(4)
(2,3)表示的是第2排第3列的位置,(3,2)表示的是
第3排第2列的位置,所以它们表示的位置不相同.
一般地,若a≠b,(a,b)与(b,a)表示的位置不相同.
用有序数对来描述物体(点)的位置,其中“有序”
是指(a,b)(a≠b)与(b,a)中a与b的前后顺序不同,描述
的位置就不同,如例题中的(3,4)和(4,3)表示不同的
两个位置;“数对”是指必须有两个数才能确定某点
的位置.
新知小结
1
用x和y组成一个有序数对,可以写成( )
A.(x,y)
B.(y,x)
C.
x,y或y,x
D.(x,y)或(y,x)
D
巩固新知
2
一个有序数对可以( )
A.确定一个点的位置
B.确定两个点的位置
C.确定一个或两个点的位置
D.不能确定点的位置
A
3
下列关于有序数对的说法正确的是( )
A.(2,3)与(3,2)表示的位置相同
B.(m,n)与(n,m)表示的位置一定不同
C.(2,-3)与(-3,2)是表示不同位置的两个有
序数对
D.(-1,-1)与(-1,-1)不是同一位置的点
C
3
知识点
用有序数对表示位置
用有序实数对确定位置:
定义:有顺序的两个数a与b组成的数对,叫做有
序数对,记作(a,b).
作用:平面上每一个点都对应着一个有序数对,
每一个有序数对都对应着一个点,因此,利用有
序数对可以准确地描述物体的位置,
即:平面上的点?有序数对.
合作探究
座位问题:
讲台
1
2
3
4
5
6
7
横排
1
2
3
4
5
6
若我们约定“列数在前,排数在后”.
请在教室找到如下表用数对表示的同学位置.
数对
(1,3)
(3,1)
(2,4)
(4,2)
(3,6)
(6,3)
约定:
列数在前
排数在后
温馨提示
数对是有顺序的!
[中考·盐城]如图,已知棋子“卒”表示为(-2,3),棋子“马”表示为(1,3),则棋子“炮”表示为________.
例3
先由“卒”(-2,3),“马”(1,3)确定“行”“列”序号,再写出“炮”的有序数对.
答案:(3,2)
导引:
(3,2)
利用行、列定位法确定点的位置时,首先确定平面内行、列的序号,然后写出表示平面上点的位置的有序数对.
新知小结
1
如图,甲处表示2街与5巷的十字路口,乙处表示5街与2巷的十字路口.
如果用(2,5)表示甲处的位置,那么“(2,
5)
→
(3,5)→(4,5)→(5,5)→(5,
4)
→(5,
3)→(5,
2)”表示从甲处到乙处的一种路线.
请你用这种形式
写出几种从甲处到乙处的路线.
巩固新知
答案不唯一,
如:(2,5)→(2,4)→(2,3)→(2,2)→(3,2)→(4,2)→(5,2);
(2,5)→(2,4)→(3,4)→(3,3)→(4,3)→(4,2)→(5,2).
解:
2
观察中国象棋的棋盘(如图),其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进4”后到达B
点,则表示B点位置
的数对是________.
(4,7)
3
小明坐在第5行第6列,简记为(5,6),小刚坐在第7行第4列,应记为( )
A.(7,4)
B.(4,7)
C.(7,5)
D.(7,6)
A
4
如图所示,小亮从学校到家所走最短路线是( )
(3,2)→(3,1)→(0,1)
B.(2,2)→(2,1)→(1,1)→(0,1)
C.(2,2)→(2,3)→(0,3)→(0,1)
D.(2,2)→(2,0)→(0,0)→(0,1)
B
确定平面内物体位置的方法有:
(1)行列定位法;
(2)极坐标定位法;
(3)经纬度定位法;
(4)区域定位法;
(5)网格定位法.
1
知识小结
归纳新知
不管采用哪种定位法,平面内确定位置都需要两个数据,特别是用一对数表示位置时,应注意这对数是有顺序的,顺序不同表示的位置不同.
如图是小岗在镜子中看到的自己的脸,他对妹妹说:如果我用有序数对(0,2)表示左眼,用有序数对(2,2)表示右眼,那么嘴的位置可以表示成( )
A.(1,2)
B.(2,1)
C.(1,0)
D.(0,1)
易错点:不能根据题目信息正确确定参照点
2
易错小结
C
根据小岗表示两眼的方法可知,参照点的位置在如图的O点,因此嘴的位置可
以表示成(1,0).本题易错之处
在于不能正确确定参照点.
两
课后练习
D
有序数对
a,b
D
C
括号
逗号
(3,2),
(5,7)(答案不唯一)
C
C
C
【答案】B
(3,240°)
再见
