2020-2021学年人教版七年级数学下册 8.1.2 二元一次方程组 课件 (51张PPT)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册 8.1.2 二元一次方程组 课件 (51张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 20:30:41 | ||
图片预览











文档简介
(共51张PPT)
第八章
8.1.2
二元一次方程组
人教版数学七年级下册
1.了解二元一次方程组的概念和二元一次方程组解的含义.
2.会体验一对数是不是二元一次方程组的解,会利用列表尝试的方法求简单的二元一次方程组的解.
学习目标
含有两个未知数,并且所含未知数的项的次数
都是1的方程叫做一元一次方程.
使方程左、右两边相等的未知数的值,叫做方
程的解.
导入新知
1
知识点
二元一次方程组
我国是一个淡水资源严重缺乏的国家.有关数据
显示,中国人均淡水资源占有量仅为美国人均淡水资
源占有量的
,
中、美两国人均淡水资源占有量之和
为13
800
m3,那么中、美两国人均淡水资源占有量各
为多少?
合作探究
我们假设中国人均淡水资源占有量为x
m3,美
国人均淡水资源占有量为y
m3,根据题意得出方程
y=5x.x+y=13
800.如果将这两个方程组合在一
起.将会得到
它们两个都是二元
一次方程,并且含有相同的未知数.
像这样共含有两个未知数的两个一次方程所组
成的一组方程,叫做二元一次方程组.
1.定义:共含有两个未知数的两个一次方程所组成的
一组方程,叫做二元一次方程组.
2.要点精析:
二元一次方程组的条件:
(1)共含有两个未知数.
(2)每个方程都是一次方程.
有下列方程组:① ②
③ ④
⑤
其中二元一次方程组有( )
A.1个 B.2个 C.3个 D.4个
B
例1
导引:①方程组中第一个方程含未知数的项xy的次
数不是1;②方程组中第二个方程不是整式
方程;③方程组中共有3个未知数.只有④
⑤满足,其中⑤中的π是常数.
识别一个方程组是否为二元一次方程组的方法:
一看方程组中的方程是否都是整式方程;
二看方程组中是不是只含有两个未知数;
三看含未知数的项的次数是不是都为1.
新知小结
1
下列方程组中,是二元一次方程组的是( )
A.
B.
C.
D.
C
巩固新知
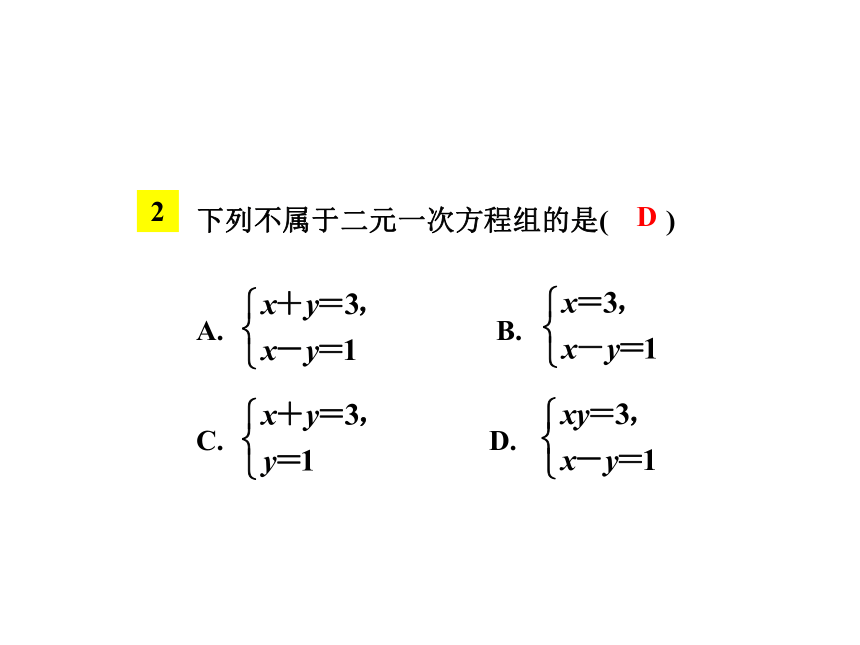
2
下列不属于二元一次方程组的是( )
A.
B.
C.
D.
D
2
知识点
二元一次方程组的解
二元一次方程组的解:
定义:二元一次方程组中各个方程的公共解,
叫做这个二元一次方程组的解.
合作探究
根据下表所给出的x的值及关于x,y的二元一次方
程,求出相应的y的值,并填入表内.
请你从上表中找出二元一次方程组
的解.
根据二元一次方程组的解的概念,找出同时满足
两个二元一次方程的公共解,即为二元一次方程
组的解.
x
1
2
3
4
5
6
7
8
9
10
y=2x
y=x+5
例2
导引:
填表如下:
从表中可以看出
解,也是二元一次方程
y=x+5的解,
所以二元一次方程组
x
1
2
3
4
5
6
7
8
9
10
y=2x
2
4
6
8
10
12
14
16
18
20
y=x+5
6
7
8
9
10
11
12
13
14
15
既是二元一次方程y=2x的
的解是
解:
本题运用定义法,检验一组数是不是某个二元一次
方程组的解,常用的方法是将这组数分别代入方程组的
每个方程中去,只要这组数满足每个方程,才能说这组
数是此方程组的解;只要发现这组数不满足其中一个方
程,即可判定这组数不是二元一次方程组的解.
新知小结
关于x,y的方程组
的解是
其中y的值被盖住了,不过仍能求出p,则p的
值是( )
A.-
B.
C.-
D.
1
A
巩固新知
已知二元一次方程组
下面说法正确的是( )
A.同时适合方程①和方程②的x,y的值是方程
组的解
B.适合方程①的x,y的值是方程组的解
C.适合方程②的x,y的值是方程组的解
D.适合方程①或方程②的x,y的值,一定是方
程组的解
2
A
【中考·泰安】方程5x+2y=-9与下列方程构成的方程组的解为
的是( )
A.x+2y=1
B.3x+2y=-8
C.5x+4y=-3
D.3x-4y=-8
3
D
【中考·舟山】若二元一次方程组
的解为
则a-b=( )
A.1
B.3
C.-
D.
4
D
3
知识点
建立二元一次方程组的模型
某中学组织七年级学生春游,原计划租用45座的客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,试问七年级学生人数是多少?原计划租用45座客车多少辆?(只列方程组)
例3
合作探究
此题中有两个未知量——七年级学生人数和原计划
租用45座客车的辆数,有两个等量关系:
(1)45×45座客车的辆数+15=七年级学生人数;
(2)60×(45座客车的辆数-1)=七年级学生人数.
设七年级学生有x人,原计划租用y辆45座客车.
根据题意,有
导引:
解:
这是与现实生活有关的方程类问题,解决这类问
题的关键是建立恰当的数学模型.列方程组的方法可
类比列一元一次方程的方法;不同的是根据实际问题
找出题目中的两个等量关系,并分别列出相应的方程.
新知小结
对下面的问题,列出二元一次方程组,并根据问题的实际意义,找出问题的解.
加工某种产品需经两道工序,第一道工序每人每天可完成900件,第二道工序每人
每天可完成1
200件.
现有7位工人参加这两道工序,应怎样安排人力,才能使每
天第一、第二道工序所完成的件数相等?
1
合作探究
设应安排x人参加第一道工序,y人参加第二道
工序,根据题意得
方程组整理为
因为x,y只能取
正整数,并且都小于7,可以看出当x=4,y=3时能满足方程组,所以应安排4人参加第一道工序,3人参加第二道工序.
解:
若单项式5xa+by3与
x5ya-b是同类项,则a,b
的值分别为( )
A.a=4,b=1
B.a=-4,b=1
C.a=4,b=-1
D.a=-4,b=-1
2
A
【中考·内江】端午节前夕,某超市用1
680元购进A、B两种商品共60件,其中A型商品每件
24元,B型商品每件36元.设购买A型商品x件、B型商品y件,依题意列方程组正确的是( )
A.
B.
C.
D.
3
B
【中考·茂名】我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )
A.
B.
C.
D.
4
C
1.二元一次方程组的特征:
(1)整个方程组(不是方程组中的每个方程)含有且
只含有两个未知数;
(2)每个方程都是一次方程;
(3)每个方程都是整式方程.
1
知识小结
归纳新知
2.
二元一次方程组的解:
(1)常见的二元一次方程组一般都只有一组解(有时
无解);
(2)只要告诉一组值是某个二元一次方程组的解,
就说明这组值是方程组中每个方程的解;
(3)方程组的解一定是方程组中每个方程的解;而
方程组中的某一方程的解不一定是方程组的解.
2
易错小结
判断
是否是二元一次方程组
的解.
解:
将
分别代入方程①和方程②中,得4x+2y
=2成立,x+y=-1不成立,所以
不是方程组
的解.
本题中方程组的解应是方程组中两个方程的公
共解.此题易错之处在于只将
代入方程①后,就进行判断,从而得出错误结论.
易错点:对二元一次方程组的解理解不透彻,导致
在检验时出错
1.有________未知数,含有每个未知数的项的次数都是1,将这样的两个方程合在一起组成的方程组叫做二元一次方程组.二元一次方程组满足的条件:
(1)_______________________________;
(2)每个方程都是___________方程.
两个
共含有两个未知数
一次
课后练习
D
3.一般地,二元一次方程组的两个方程的__________,叫做二元一次方程组的解.二元一次方程组的解指的是同时满足两个方程的一对________的值,方程组的解必定是其中每一个方程的解,但方程组中方程的解不一定是方程组的解.
公共解
未知数
A
B
B
【点拨】将x=3代入x+y=5,可得y=2,将x=3,y=2代入x+my=7,得3+2m=7,解得m=2.
【点拨】方程ax+cy=1两边同乘x,cx-by=2两边同乘y后相减,然后把方程组的解代入,整理可得a,b间的关系.
D
8.建立二元一次方程组的模型,其实质是根据题中所反映的数量关系,依据相关定义、性质分别列出________________,并组成方程组.
二元一次方程
9.(2019·邵阳)某出租车起步价所包含的路程为0
km~2
km,超过2
km的部分按每千米另收费(不足1
km按1
km算).津津乘坐这种出租车走了7
km,付了16元;盼盼乘坐这种出租车走了13
km,付了28元.设这种出租车的起步价为x元,超过2
km后每千米收费y元,则下列方程正确的是( )
【答案】D
10.(2020·宁波)我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
【答案】A
【点拨】将各组解代入方程来验证,使两个方程都成立的就是方程组的解.
解:③④⑤是方程2x+31y=-11的解.
12.已知两个二元一次方程:①3x-y=0;②7x-2y=2.
(1)对于给出的x值,在下表中分别写出对应的y值;
-6
x
-2
-1
0
1
2
3
①y
?
?
?
?
?
?
②y
?
?
?
?
?
?
-3
0
3
6
9
-8
-4.5
-1
2.5
6
9.5
13.根据有关信息设未知数,列二元一次方程组(不解方程组).
母亲节那天,很多同学给妈妈准备了鲜花和礼盒,从图中信息可求1束鲜花和1个礼盒的价格.
根据魏子航和朱明浩两名同学的对话,求a2
023+b的值.
【思路点拨】将两人得出的解分别代入没有看错系数的方程中,即可得到关于b,a的方程,从而求得a,b的值.
再见
第八章
8.1.2
二元一次方程组
人教版数学七年级下册
1.了解二元一次方程组的概念和二元一次方程组解的含义.
2.会体验一对数是不是二元一次方程组的解,会利用列表尝试的方法求简单的二元一次方程组的解.
学习目标
含有两个未知数,并且所含未知数的项的次数
都是1的方程叫做一元一次方程.
使方程左、右两边相等的未知数的值,叫做方
程的解.
导入新知
1
知识点
二元一次方程组
我国是一个淡水资源严重缺乏的国家.有关数据
显示,中国人均淡水资源占有量仅为美国人均淡水资
源占有量的
,
中、美两国人均淡水资源占有量之和
为13
800
m3,那么中、美两国人均淡水资源占有量各
为多少?
合作探究
我们假设中国人均淡水资源占有量为x
m3,美
国人均淡水资源占有量为y
m3,根据题意得出方程
y=5x.x+y=13
800.如果将这两个方程组合在一
起.将会得到
它们两个都是二元
一次方程,并且含有相同的未知数.
像这样共含有两个未知数的两个一次方程所组
成的一组方程,叫做二元一次方程组.
1.定义:共含有两个未知数的两个一次方程所组成的
一组方程,叫做二元一次方程组.
2.要点精析:
二元一次方程组的条件:
(1)共含有两个未知数.
(2)每个方程都是一次方程.
有下列方程组:① ②
③ ④
⑤
其中二元一次方程组有( )
A.1个 B.2个 C.3个 D.4个
B
例1
导引:①方程组中第一个方程含未知数的项xy的次
数不是1;②方程组中第二个方程不是整式
方程;③方程组中共有3个未知数.只有④
⑤满足,其中⑤中的π是常数.
识别一个方程组是否为二元一次方程组的方法:
一看方程组中的方程是否都是整式方程;
二看方程组中是不是只含有两个未知数;
三看含未知数的项的次数是不是都为1.
新知小结
1
下列方程组中,是二元一次方程组的是( )
A.
B.
C.
D.
C
巩固新知
2
下列不属于二元一次方程组的是( )
A.
B.
C.
D.
D
2
知识点
二元一次方程组的解
二元一次方程组的解:
定义:二元一次方程组中各个方程的公共解,
叫做这个二元一次方程组的解.
合作探究
根据下表所给出的x的值及关于x,y的二元一次方
程,求出相应的y的值,并填入表内.
请你从上表中找出二元一次方程组
的解.
根据二元一次方程组的解的概念,找出同时满足
两个二元一次方程的公共解,即为二元一次方程
组的解.
x
1
2
3
4
5
6
7
8
9
10
y=2x
y=x+5
例2
导引:
填表如下:
从表中可以看出
解,也是二元一次方程
y=x+5的解,
所以二元一次方程组
x
1
2
3
4
5
6
7
8
9
10
y=2x
2
4
6
8
10
12
14
16
18
20
y=x+5
6
7
8
9
10
11
12
13
14
15
既是二元一次方程y=2x的
的解是
解:
本题运用定义法,检验一组数是不是某个二元一次
方程组的解,常用的方法是将这组数分别代入方程组的
每个方程中去,只要这组数满足每个方程,才能说这组
数是此方程组的解;只要发现这组数不满足其中一个方
程,即可判定这组数不是二元一次方程组的解.
新知小结
关于x,y的方程组
的解是
其中y的值被盖住了,不过仍能求出p,则p的
值是( )
A.-
B.
C.-
D.
1
A
巩固新知
已知二元一次方程组
下面说法正确的是( )
A.同时适合方程①和方程②的x,y的值是方程
组的解
B.适合方程①的x,y的值是方程组的解
C.适合方程②的x,y的值是方程组的解
D.适合方程①或方程②的x,y的值,一定是方
程组的解
2
A
【中考·泰安】方程5x+2y=-9与下列方程构成的方程组的解为
的是( )
A.x+2y=1
B.3x+2y=-8
C.5x+4y=-3
D.3x-4y=-8
3
D
【中考·舟山】若二元一次方程组
的解为
则a-b=( )
A.1
B.3
C.-
D.
4
D
3
知识点
建立二元一次方程组的模型
某中学组织七年级学生春游,原计划租用45座的客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,试问七年级学生人数是多少?原计划租用45座客车多少辆?(只列方程组)
例3
合作探究
此题中有两个未知量——七年级学生人数和原计划
租用45座客车的辆数,有两个等量关系:
(1)45×45座客车的辆数+15=七年级学生人数;
(2)60×(45座客车的辆数-1)=七年级学生人数.
设七年级学生有x人,原计划租用y辆45座客车.
根据题意,有
导引:
解:
这是与现实生活有关的方程类问题,解决这类问
题的关键是建立恰当的数学模型.列方程组的方法可
类比列一元一次方程的方法;不同的是根据实际问题
找出题目中的两个等量关系,并分别列出相应的方程.
新知小结
对下面的问题,列出二元一次方程组,并根据问题的实际意义,找出问题的解.
加工某种产品需经两道工序,第一道工序每人每天可完成900件,第二道工序每人
每天可完成1
200件.
现有7位工人参加这两道工序,应怎样安排人力,才能使每
天第一、第二道工序所完成的件数相等?
1
合作探究
设应安排x人参加第一道工序,y人参加第二道
工序,根据题意得
方程组整理为
因为x,y只能取
正整数,并且都小于7,可以看出当x=4,y=3时能满足方程组,所以应安排4人参加第一道工序,3人参加第二道工序.
解:
若单项式5xa+by3与
x5ya-b是同类项,则a,b
的值分别为( )
A.a=4,b=1
B.a=-4,b=1
C.a=4,b=-1
D.a=-4,b=-1
2
A
【中考·内江】端午节前夕,某超市用1
680元购进A、B两种商品共60件,其中A型商品每件
24元,B型商品每件36元.设购买A型商品x件、B型商品y件,依题意列方程组正确的是( )
A.
B.
C.
D.
3
B
【中考·茂名】我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为( )
A.
B.
C.
D.
4
C
1.二元一次方程组的特征:
(1)整个方程组(不是方程组中的每个方程)含有且
只含有两个未知数;
(2)每个方程都是一次方程;
(3)每个方程都是整式方程.
1
知识小结
归纳新知
2.
二元一次方程组的解:
(1)常见的二元一次方程组一般都只有一组解(有时
无解);
(2)只要告诉一组值是某个二元一次方程组的解,
就说明这组值是方程组中每个方程的解;
(3)方程组的解一定是方程组中每个方程的解;而
方程组中的某一方程的解不一定是方程组的解.
2
易错小结
判断
是否是二元一次方程组
的解.
解:
将
分别代入方程①和方程②中,得4x+2y
=2成立,x+y=-1不成立,所以
不是方程组
的解.
本题中方程组的解应是方程组中两个方程的公
共解.此题易错之处在于只将
代入方程①后,就进行判断,从而得出错误结论.
易错点:对二元一次方程组的解理解不透彻,导致
在检验时出错
1.有________未知数,含有每个未知数的项的次数都是1,将这样的两个方程合在一起组成的方程组叫做二元一次方程组.二元一次方程组满足的条件:
(1)_______________________________;
(2)每个方程都是___________方程.
两个
共含有两个未知数
一次
课后练习
D
3.一般地,二元一次方程组的两个方程的__________,叫做二元一次方程组的解.二元一次方程组的解指的是同时满足两个方程的一对________的值,方程组的解必定是其中每一个方程的解,但方程组中方程的解不一定是方程组的解.
公共解
未知数
A
B
B
【点拨】将x=3代入x+y=5,可得y=2,将x=3,y=2代入x+my=7,得3+2m=7,解得m=2.
【点拨】方程ax+cy=1两边同乘x,cx-by=2两边同乘y后相减,然后把方程组的解代入,整理可得a,b间的关系.
D
8.建立二元一次方程组的模型,其实质是根据题中所反映的数量关系,依据相关定义、性质分别列出________________,并组成方程组.
二元一次方程
9.(2019·邵阳)某出租车起步价所包含的路程为0
km~2
km,超过2
km的部分按每千米另收费(不足1
km按1
km算).津津乘坐这种出租车走了7
km,付了16元;盼盼乘坐这种出租车走了13
km,付了28元.设这种出租车的起步价为x元,超过2
km后每千米收费y元,则下列方程正确的是( )
【答案】D
10.(2020·宁波)我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )
【答案】A
【点拨】将各组解代入方程来验证,使两个方程都成立的就是方程组的解.
解:③④⑤是方程2x+31y=-11的解.
12.已知两个二元一次方程:①3x-y=0;②7x-2y=2.
(1)对于给出的x值,在下表中分别写出对应的y值;
-6
x
-2
-1
0
1
2
3
①y
?
?
?
?
?
?
②y
?
?
?
?
?
?
-3
0
3
6
9
-8
-4.5
-1
2.5
6
9.5
13.根据有关信息设未知数,列二元一次方程组(不解方程组).
母亲节那天,很多同学给妈妈准备了鲜花和礼盒,从图中信息可求1束鲜花和1个礼盒的价格.
根据魏子航和朱明浩两名同学的对话,求a2
023+b的值.
【思路点拨】将两人得出的解分别代入没有看错系数的方程中,即可得到关于b,a的方程,从而求得a,b的值.
再见
