同底数幂乘法(授课课件)
图片预览





文档简介
(共13张PPT)
——选自人教版八年级上册第十 五章第一节第一小节
主讲人:杨淑敏
求n个相同因数的积的运算
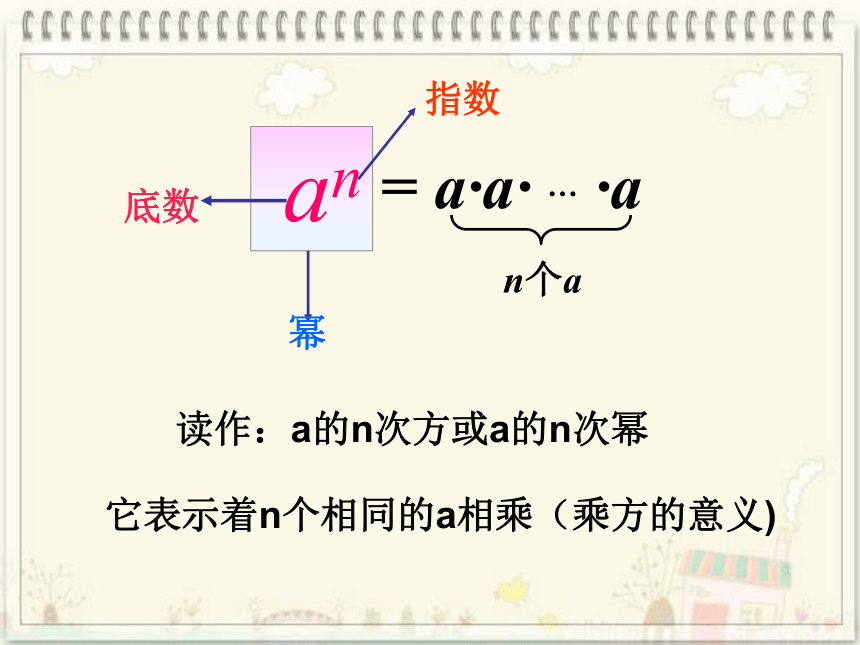
幂
读作:a的n次方或a的n次幂
它表示着n个相同的a相乘(乘方的意义)
= a·a· … ·a
n个a
an
底数
幂
指数
一种电子计算机每秒可以进行1012次运算,它工作103秒可以进行多少次运算?你能用学过的知识解决吗?
分析:它工作103秒可以进行的运算次数是1012×103.怎样计算1012×103
1012×103 =
1015
探一探.猜一猜
探
(2)23×24 =
(3)a2 · a3 =
(1)103×102=
105
=10(3+2)
27
=2(3+4)
a5
=a (2+3)
猜
从上面的计算结果,你发现了什么规律
那么,我们把第三小题改为am an ,该怎么算呢? (m、n都是正整数时)
一般地:
am an
= a(m+n)
= (a a … a)
= a a … a
(m)个
(n)个
(m+n )个
(a a … a)
对于任意的底数a与任意正整数m,n
am · an = am+n (当m、n都是正整数)
运算方法:
即同底数幂相乘,底数不变,指数相加.
(1)10a ×10b (2)x2 · x5(3)x2 · x5 · x
(4) (x+y)3 · (x+y)4
10a×10b=
10 (a+b)
x2 · x5=
x (2+5)
=x7
x2 · x5 · x =
(x2 · x5 )· x=x7· x
=x (7+1) =x8
(利用公式: am · an = am+n )
(x+y)3 · (x+y)4=
公式中的a可代表一个数、字母,代数式等.
(x+y)3+4=
(x+y)7
(1)a5 · b2=
(2)b5 + b5 =
(3)x5 ·x5 =
2b5
x10
所以在计算的过程中同学们要注意什么呢?
a5 · b2
条件:①乘法 ②同底数幂
结果:①底数不变 ②指数相加
(1)a5 · ( )=a8
(2) 若8×4=2x,则x=__________
(3) 已知:am=2, an=3.求am+n =?.
同底数幂相乘,底数不变,指数相加.
am · an =a m+n (m,n都是正整数)
计算过程中应注意什么?
八字:同底,相乘,不变,相加
课本 P142 练习题
思考题: 如果x m-n ×x 2n+1=x 11,且
ym-1×y 4-n =y 7,求m , n的值
——选自人教版八年级上册第十 五章第一节第一小节
主讲人:杨淑敏
求n个相同因数的积的运算
幂
读作:a的n次方或a的n次幂
它表示着n个相同的a相乘(乘方的意义)
= a·a· … ·a
n个a
an
底数
幂
指数
一种电子计算机每秒可以进行1012次运算,它工作103秒可以进行多少次运算?你能用学过的知识解决吗?
分析:它工作103秒可以进行的运算次数是1012×103.怎样计算1012×103
1012×103 =
1015
探一探.猜一猜
探
(2)23×24 =
(3)a2 · a3 =
(1)103×102=
105
=10(3+2)
27
=2(3+4)
a5
=a (2+3)
猜
从上面的计算结果,你发现了什么规律
那么,我们把第三小题改为am an ,该怎么算呢? (m、n都是正整数时)
一般地:
am an
= a(m+n)
= (a a … a)
= a a … a
(m)个
(n)个
(m+n )个
(a a … a)
对于任意的底数a与任意正整数m,n
am · an = am+n (当m、n都是正整数)
运算方法:
即同底数幂相乘,底数不变,指数相加.
(1)10a ×10b (2)x2 · x5(3)x2 · x5 · x
(4) (x+y)3 · (x+y)4
10a×10b=
10 (a+b)
x2 · x5=
x (2+5)
=x7
x2 · x5 · x =
(x2 · x5 )· x=x7· x
=x (7+1) =x8
(利用公式: am · an = am+n )
(x+y)3 · (x+y)4=
公式中的a可代表一个数、字母,代数式等.
(x+y)3+4=
(x+y)7
(1)a5 · b2=
(2)b5 + b5 =
(3)x5 ·x5 =
2b5
x10
所以在计算的过程中同学们要注意什么呢?
a5 · b2
条件:①乘法 ②同底数幂
结果:①底数不变 ②指数相加
(1)a5 · ( )=a8
(2) 若8×4=2x,则x=__________
(3) 已知:am=2, an=3.求am+n =?.
同底数幂相乘,底数不变,指数相加.
am · an =a m+n (m,n都是正整数)
计算过程中应注意什么?
八字:同底,相乘,不变,相加
课本 P142 练习题
思考题: 如果x m-n ×x 2n+1=x 11,且
ym-1×y 4-n =y 7,求m , n的值
