2020-2021学年高一物理必修第二册第五章第四节抛体运动的规律能力提升训练集
文档属性
| 名称 | 2020-2021学年高一物理必修第二册第五章第四节抛体运动的规律能力提升训练集 |

|
|
| 格式 | doc | ||
| 文件大小 | 1016.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-16 00:00:00 | ||
图片预览




文档简介
2020-2021学年高一物理必修第二册第五章第四节抛体运动的规律能力提升训练集
一、单选题
1.如图所示,小球以一定的水平速度离开水平桌面,经过落地。不计空气阻力,重力加速度取,则桌面离地高度为( )
A.
B.
C.
D.
2.如图所示,A、B两个小球从同一竖直线上的不同位置水平拋出,结果它们同时落在地面上的同一点C,已知A离地面的高度是B离地面高度的2倍,则A、B两个球的初速度之比vA∶vB为( )
A.1∶2
B.2∶1
C.∶1
D.1∶
3.在同一水平直线上的两位置分别沿同方向水平抛出两小球A和B,其运动轨迹如图所示,不计空气阻力,要使两球在空中相遇,则必须(
)
A.先抛出A球
B.先抛出B球
C.A球的初速度小于B球的初速度
D.A球的初速度大于B球的初速度
4.如图所示,在某次演习中,轰炸机沿水平方向投放一枚炸弹,经过时间炸弹恰好垂直击中山坡上的目标,已知炸弹平抛的初速度。不计空气阻力,则山坡倾角为( )(重力加速度g取)
A.15°
B.30°
C.45°
D.60°
5.将一只苹果水平抛出,苹果在空中依次从竖直方向飞过三个完全相同的窗户1、2、3,图中曲线为苹果在空中运行的轨迹。若不计空气阻力的影响,以下说法正确的是( )
A.苹果通过3个窗户所用的时间相同
B.苹果通过第1个窗户的平均速度最大
C.苹果通过3个窗户的位移相同
D.苹果通过第3个窗户的位移最小
6.军事演习中,M点的正上方离地H高处的蓝军飞机以水平速度v1投掷一颗炸弹攻击地面目标,反应灵敏的红军的地面高炮系统同时在M点右方地面上N点以速度v2斜向左上方发射拦截炮弹,两弹恰在M、N连线的中点正上方相遇爆炸,不计空气阻力,则发射后至相遇过程( )
A.两弹飞行的轨迹重合
B.初速度大小关系为v1=v2
C.拦截弹相对攻击弹做匀速直线运动
D.两弹相遇点一定在距离地面H高度处
7.如图所示,从某高度水平抛出一小球,经过时间t到达一竖直墙面时,速度与水平方向的夹角为θ。不计空气阻力,重力加速度为g。下列说法正确的是(
)
A.小球水平抛出时的初速度大小为gtcotθ
B.小球到达竖直墙时的速度大小为gtcosθ
C.小球在时间t内的位移大小为
D.小球在时间t内的位移方向与水平方向的夹角为
8.某同学参加学校的跳远比赛,其运动轨迹可以简化为如图所示,该同学以速率v沿与水平地面成某一角度方向跳出,运动过程中离开地面的最大高度为,若该同学可视为质点,不计空气阻力,重力加速度为g,则该同学本次跳远的成绩为( )
A.
B.
C.
D.
9.如图所示,A、B两小球从相同高度同时水平抛出,经过时间t在空中相遇,若两球的抛出速度都变为原来的2倍,则两球从抛出到相遇经过的时间为( )
A.
B.
C.
D.
10.如图所示,从倾角为的足够长的斜面顶端以速度抛出一个小球,落在斜面上点,小球落在斜面上的速度与斜面的夹角,若把初速度变为,小球仍然落在斜面的情况下,以下说法正确的是( )
A.夹角将变为原来的倍
B.夹角不变
C.空中的运动时间不变
D.小球的水平位移和竖直位移之比变为原来的倍
11.如图所示,斜槽轨道末端切线水平,斜面AB上端位于斜槽轨道末端、下瑞位于水平地面上。一个可视为质点的钢球从斜槽上某处由静止释放,以速度v0从斜槽末端飞出经历时间t落在地面上的D点。把钢球从斜槽上较低位置由静止释放,以速度从斜槽末端飞出落在斜面中点C点。不计空气阻力的作用,则钢球从斜槽末端飞出到落到斜面中点C所经历的时间为( )
A.
B.
C.
D.
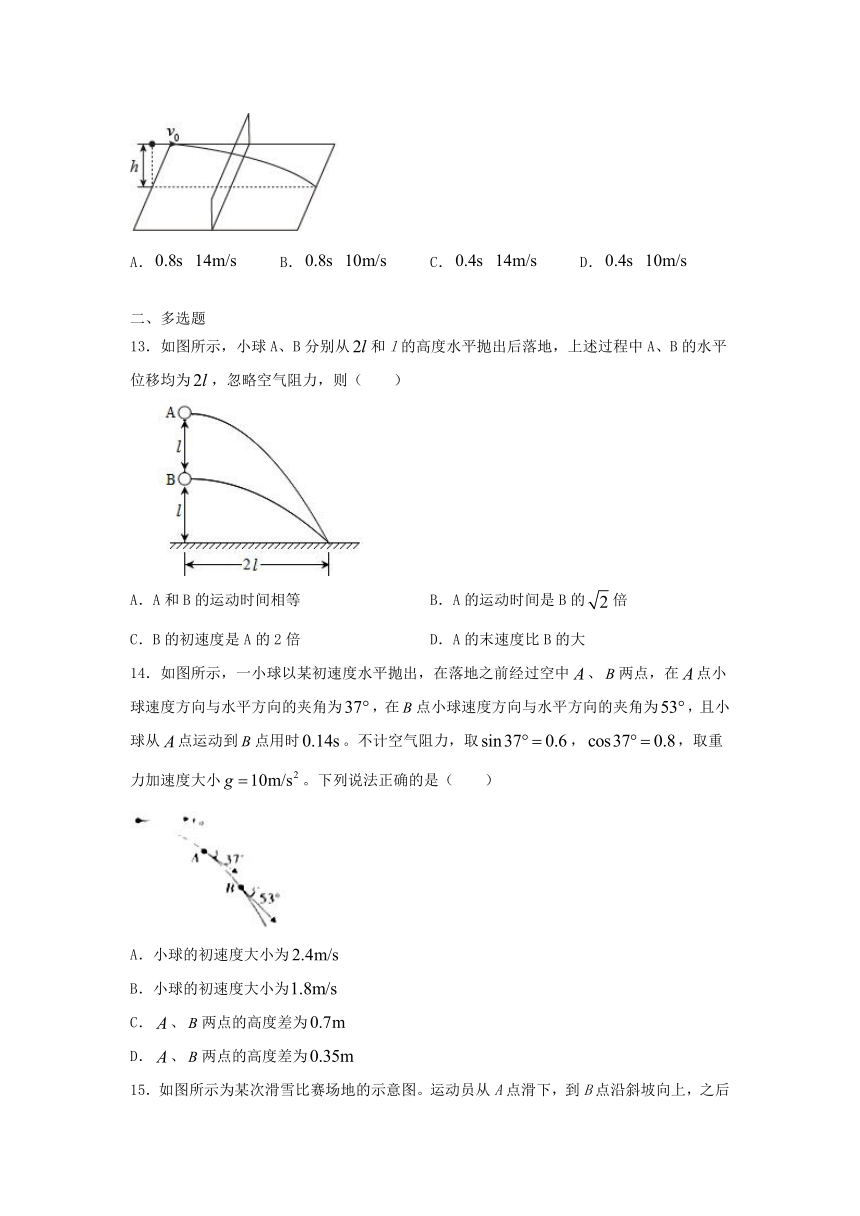
12.2020年7月,中国女排在宁波北仑基地进行第二阶段集训,目标是在东京奥运会上完成卫冕。如图所示,排球运动员在发球线正对球网跳起发球,在距地面高度为处使质量的排球(可视为质点)以的初速度水平飞出。不考虑空气阻力,重力加速度取,则排球从被扣出到着地的时间和排球即将着地时的速率分别为(
)
A.
B.
C.
D.
二、多选题
13.如图所示,小球A、B分别从和l的高度水平抛出后落地,上述过程中A、B的水平位移均为,忽略空气阻力,则( )
A.A和B的运动时间相等
B.A的运动时间是B的倍
C.B的初速度是A的2倍
D.A的末速度比B的大
14.如图所示,一小球以某初速度水平抛出,在落地之前经过空中、两点,在点小球速度方向与水平方向的夹角为,在点小球速度方向与水平方向的夹角为,且小球从点运动到点用时。不计空气阻力,取,,取重力加速度大小。下列说法正确的是(
)
A.小球的初速度大小为
B.小球的初速度大小为
C.、两点的高度差为
D.、两点的高度差为
15.如图所示为某次滑雪比赛场地的示意图。运动员从A点滑下,到B点沿斜坡向上,之后从C点飞出,最后落在D点,设运动员在段受到的阻力恒定,不计空气阻力,运动员没有做任何动作,滑板与坡面间的动摩擦因数为0.2,段的倾角为53°,则运动员从B点运动到D点,在水平方向和竖直方向的分速度、随时间t变化关系正确的是(
)
A.
B.
C.
D.
三、实验题
16.图甲是“研究平抛物体运动”的实验装置图,通过描点画出平抛小球的运动轨迹。
(1)以下是实验过程中的一些做法,其中合理的有___________。
A.安装斜槽轨道,其末端是否保持水平不影响实验的研究
B.每次小球释放的初始位置可以任意选择
C.每次小球应从同一高度由静止释放
D.为描出小球的运动轨迹,描绘的点可以用折线连接
(2)实验得到平抛小球的运动轨迹,在轨迹上取一些点,以平抛起点O为坐标原点,测量它们的水平坐标x和竖直坐标y,图乙中y—x2图像能说明平抛小球运动轨迹为抛物线的是___________。
(3)图丙是某同学根据实验画出的平抛小球的运动轨迹,O为平抛的起点,在轨迹上任取两点A、B,测得A、B两点纵坐标y1=5.0
cm,y2=45.0
cm,A、B两点水平间距x=20.0
cm。则平抛小球的初速度v0为___________
m/s。(g取10
m/s2,计算结果保留两位有效数字。)
17.在“探究平抛运动规律”的实验中:
(1)在做“研究平抛运动”的实验时,让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹,为了能较准确地描绘运动轨迹。下列对实验过程的描述哪些是正确的(______)
A.通过调节使斜槽的末端保持水平
B.每次静止释放小球的位置必须相同
C.小球运动时应与木板上的白纸相接触
D.将球的位置记录在纸上后,取下纸,将点连成平滑曲线
(2)某同学实验时得到了如图所示物体的运动轨迹。O、B、C三点的位置在运动轨迹上已标出,O_______(是或不是)抛出点。
(3)则小球平抛的初速度______。
(4)小球运动到B点的速度vB=________m/s(计算结果均保留两位有效数字)
四、解答题
18.跳台滑雪是勇敢者的运动,它是利用山势特别建造的跳台所进行的。运动员穿专用滑雪板,在助滑路上获得高速后飞出,在空中飞行一段距离后着陆。如图所示,设一位运动员由A点沿水平方向跃起,到B点着陆时,测得AB间距离L=40m,山坡倾角θ=30°(不计空气阻力,g取10m/s2),求:
(1)运动员起跳的速度;
(2)运动员在空中飞行的时间;
(3)运动员经多长时间离坡面距离最大。
19.如图所示,上端开口的圆柱形桶固定在水平地面上,某同学将质量为的小球,从点顺着桶的某条直径方向水平抛出,小球恰好从桶的左侧上边沿进入桶内并打在桶的右下角。已知点到桶左边沿的水平距离,桶的高度,点离地面的高度,桶底和桶壁的厚度均不计,重力加速度大小。求:
(1)小球水平抛出时的速度大小和桶的直径;
(2)为使小球总能落入桶内,则小球从点水平抛出时的速度大小的取值范围。
20.如图所示,一小球自平台上水平抛出,恰好落在台的一倾角为的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差,重力加速度,,,求:
(1)小球水平抛出的初速度是多少?
(2)面顶端与平台边缘的水平距离是多少?
(3)若斜面顶端高,则小球离开平台后经多长时间到达斜面底端?
21.在某项娱乐活动中,要求参与者通过一光滑的斜面将质量为m的物块送上高处的水平传送带后运送到网兜内。斜面长度为l,倾角为θ=,传送带距地面高度为l,传送带的长度为3l,传送带表面的动摩擦因数,传送带一直以速度顺时针运动。当某参与者第一次试操作时瞬间给予小物块一初速度只能将物块刚好送到斜面顶端;第二次调整初速度,恰好让物块水平冲上传送带并成功到达网兜。求:
(1)第一次小物块获得的初速度;
(2)第二次小物块滑上传送带的速度和传送带距斜面的水平距离;
(3)假如小物块是一小煤块,第二次小煤块通过传送带过程中留在传送带上的痕迹长度。
参考答案
1.C
小球离开桌面后做平抛运动,则桌面离地高度为
故选C。
2.D
根据
可得
则AB两球的时间之比为
根据x=vt,则
3.D
AB.平抛运动的落地时间只与竖直高度有关,要使两球在空中相遇必须同时抛出,故AB错误;
CD.因A球在后B球在前,则需要A球的初速度大于B球的初速度,故D正确C错误。
故选D。
4.B
炸弹在空中做平抛运动,炸弹击中目标时竖直分速度
设炸弹击中目标时速度方向与竖直方向的夹角为α,如图所示,则
得α=30°
根据几何关系可知山坡倾角θ=α=30°,故ACD错误,B正确。
故选B。
5.D
AB.苹果在竖直方向做自由落体运动,通过三个窗户的竖直高度相同,竖直方向分速度越来越大,通过第1个窗户时竖直方向的平均速度最小,平均合速度也最小,时间最长,AB错误;
CD.水平方向上,由x=v0t可知,通过第3个窗户的水平位移最小,通过三个窗户的竖直位移相同,则通过第3个窗户的合位移最小,C错误,D正确。
6.C
A.两弹在M、N连线的中点正上方相遇,只能说明末位置相同,不能说明运动轨迹重合,故A错误;
B.由于两弹恰在M、N连线的中点正上方相遇,说明它们的水平位移大小相等,又由于运动的时间相同,所以它们在水平方向上的速度相同,即
v2cosθ=v1
所以
v2>v1
故B错误;
C.两弹都只受到重力,都做匀变速运动,加速度相同,所以拦截弹相对攻击弹做匀速直线运动,故C正确;
D.根据题意只能求出两弹运动时间相同,但不知道拦截炮弹竖直方向初速度的具体值,所以不能判断两弹相遇点距离地面的高度,所以D错误。
7.A
AB.小球做平抛运动,将其分解为水平方向的匀速直线运动,和竖直方向的自由落体运动,则水平方向有
x
=
v0t
竖直方向有
y
=
gt2,vy
=
gt
将小球到达竖直墙面时的速度进行分解,如图所示
由图可知
v0
=
=
=
gtcotθ,v
=
=
A正确、B错误;
C.由选项AB知
x
=
v0t,y
=
gt2
则小球的位移L为
L
=
=
C错误;
D.设小球在时间t内的位移方向与水平方向的夹角为α,则
D错误。
8.A
设速度v与水平方向夹角为θ,则
运动时间
水平位移
联立解得
故选A。
9.C
设第一次抛出时A球的速度为v1,B球的速度为v2,则A、B间的水平距离
第二次抛出时两球的速度为第一次的2倍,但两球间的水平距离不变,则
联立解得
故选C。
10.B
AB.速度与水平方向夹角的正切值
位移与水平方向的正切值
可知速度方向与水平方向夹角正切值是位移与水平方向夹角正切值的2倍。因为位移与水平方向夹角不变,则速度与水平方向夹角不变,所以两个角度之差,即α不变,A错误B正确;
C.根据
解得小球在空中运动时间为
若初速度变为原来的倍,则小球在空中的运动时间变为原来的倍,C错误;
D.小球的水平位移和竖直位移之比
因为若初速度变为原来的倍,小球在空中的运动时间变为原来的倍,则位移之比没有变化,D错误。
11.D
钢球水平飞出至D点运动的时间与运动到B点时间相同,对于落到斜面AB的物体,运动时间满足关系式
其中l为斜面长度,θ为斜面倾角,由此表达式可知
,
12.B
排球飞出后做平抛运动,竖直方向的分运动为自由落体运动,由
代入数据解得
即将着地的竖直速度
即将着地的水平速度
排球即将着地时的速率
13.BD
AB.小球水平抛出后在竖直方向自由下落,A、B分别满足
可解得,,故A错误,B正确;
C.小球在水平方向做匀速直线运动,由
可得A、B的初速度分别为,,故C错误;
D.抛出至落地过程,根据动能定理有
代入数据可解得A、B球落地速度分别为,,可知A的末速度比B的大,D正确。
14.AD
AB.根据速度的分解和竖直方向自由落体运动可知:
,,vBy-vAy=gt
解得小球的初速度大小为,故A正确B错误;
CD.根据以上分析可知,两点竖直速度分别为1.8m/s和3.2m/s。故、两点的高度差
故C错误D正确。
15.BD
AB.运动员在BC部分运动时,受到重力、支持力和斜坡的摩擦力,合力沿斜面向下,所以此时水平方向为匀减速运动,在CD部分运动时,运动员只受重力,做斜抛运动,水平方向为匀速运动,故A错误,B正确;
CD.运动员在BC部分运动时,受到重力、支持力和斜坡的摩擦力,合力沿斜面向下,所以此时竖直方向为匀减速运动,在CD部分运动时,运动员只受重力,做斜抛运动,竖直方向为速度与加速度相反的匀变速运动,故C错误,D正确。
故选BD。
16.C
c
1.0
(1)[1]A.通过调节斜槽使末端保持水平,是为了保证小球做平抛运动,A错误;
BC.为了使每次小球做平抛运动的轨迹相同,就要使小球做平抛运动得初速度相同,故每次都要由静止从同一位置释放,B错误,C正确;
D.由于平抛运动得轨迹是一条抛物线,故应将各点用一条平滑得曲线连接起来,不能用折线,D错误。
故选C。
(2)[2]小球在水平方向做匀速直线运动,水平位移满足
竖直位移满足
联立可得
故y与x2为正比例函数,c正确。
故选c。
(3)[3]设OA过程时间t1,OB过程时间t2,在竖直方向上,由匀变速直线运动公式可得
水平方向由匀速直线运动公式可得
联立代入数据可解得v0=1.0m/s。
17.ABD
不是
2
2.5
(1)[1]A.为了保证小球的初速度水平,需调节斜槽的末端保持水平,A错误;
B.为了保证小球每次做平抛运动的初速度相等,小球每次必须从同一位置由静止释放,B正确;
C.小球做平抛运动时,不应与纸接触,避免摩擦改变运动轨迹,带来误差,C错误;
D.将球的位置记录在纸上后,取下纸,将点连成平滑曲线,并建立坐标,以便分析研究平抛运动,D正确。
故选ABD;
(2)[2]
O到B、B到C过程,水平分位移相等,即时间间隔相等,若O点是抛出点,两段竖直分位移之比应为1:3,而题中竖直分位移之比为1:2,故竖直方向有初速度,O不是抛出点;
(3)[3]竖直方向上,根据
其中t为O到B、B到C过程的时间间隔,可得
水平方向上
(4)[4]设小球经过B点时的竖直分速度为vBy,在竖直方向上有
故
18.(1)
;(2)2s;(3)1s
(1)
(2)运动员在空中飞行时,做平抛运动
,
解得
,
(3)
速度与斜面平行时,离坡面距离最大。有
tanθ==
解得
19.(1)
2m/s
;0.2m;(2)
2m/s~2.5m/s
(1)小球从P点开始到桶的左上边缘时
解得
t1=0.4s
v0=2m/s
小球下落的总时间
则桶的直径
(2)若使小球打到桶右侧上边缘,则
解得
小球从点水平抛出时的速度大小的取值范围为2m/s~2.5m/s.
20.(1);(2);(3)
(1)由题意可知:小球落到斜面上并沿斜面下滑,说明此时小球速度方向与斜面平行,否则小球会弹起,所以
,
代入数据,得
m/s,
(2)由得
水平距离为
(3)小球沿斜面做匀加速直线运动的加速度
,
初速度
且
代入数据,整理得
解得
或(不合题意舍去)
所以
21.(1);(2);(3)
(1)第一次在斜面上滑到顶端时
由运动学公式得
所以第一次小物块获得的初速度
(2)第二次恰好让物块水平冲上传送带,逆向看相当于平抛运动,竖直方向上相当于自由落体,则有
同时
由速度分解关系得第二次小物块滑上传送带的速度
传送带距斜面的水平距离
(3)当物块匀减速至传送带速度相等的时间
物块向右的位移
此过程中传送带向右的位移
划痕长度为相对位移
一、单选题
1.如图所示,小球以一定的水平速度离开水平桌面,经过落地。不计空气阻力,重力加速度取,则桌面离地高度为( )
A.
B.
C.
D.
2.如图所示,A、B两个小球从同一竖直线上的不同位置水平拋出,结果它们同时落在地面上的同一点C,已知A离地面的高度是B离地面高度的2倍,则A、B两个球的初速度之比vA∶vB为( )
A.1∶2
B.2∶1
C.∶1
D.1∶
3.在同一水平直线上的两位置分别沿同方向水平抛出两小球A和B,其运动轨迹如图所示,不计空气阻力,要使两球在空中相遇,则必须(
)
A.先抛出A球
B.先抛出B球
C.A球的初速度小于B球的初速度
D.A球的初速度大于B球的初速度
4.如图所示,在某次演习中,轰炸机沿水平方向投放一枚炸弹,经过时间炸弹恰好垂直击中山坡上的目标,已知炸弹平抛的初速度。不计空气阻力,则山坡倾角为( )(重力加速度g取)
A.15°
B.30°
C.45°
D.60°
5.将一只苹果水平抛出,苹果在空中依次从竖直方向飞过三个完全相同的窗户1、2、3,图中曲线为苹果在空中运行的轨迹。若不计空气阻力的影响,以下说法正确的是( )
A.苹果通过3个窗户所用的时间相同
B.苹果通过第1个窗户的平均速度最大
C.苹果通过3个窗户的位移相同
D.苹果通过第3个窗户的位移最小
6.军事演习中,M点的正上方离地H高处的蓝军飞机以水平速度v1投掷一颗炸弹攻击地面目标,反应灵敏的红军的地面高炮系统同时在M点右方地面上N点以速度v2斜向左上方发射拦截炮弹,两弹恰在M、N连线的中点正上方相遇爆炸,不计空气阻力,则发射后至相遇过程( )
A.两弹飞行的轨迹重合
B.初速度大小关系为v1=v2
C.拦截弹相对攻击弹做匀速直线运动
D.两弹相遇点一定在距离地面H高度处
7.如图所示,从某高度水平抛出一小球,经过时间t到达一竖直墙面时,速度与水平方向的夹角为θ。不计空气阻力,重力加速度为g。下列说法正确的是(
)
A.小球水平抛出时的初速度大小为gtcotθ
B.小球到达竖直墙时的速度大小为gtcosθ
C.小球在时间t内的位移大小为
D.小球在时间t内的位移方向与水平方向的夹角为
8.某同学参加学校的跳远比赛,其运动轨迹可以简化为如图所示,该同学以速率v沿与水平地面成某一角度方向跳出,运动过程中离开地面的最大高度为,若该同学可视为质点,不计空气阻力,重力加速度为g,则该同学本次跳远的成绩为( )
A.
B.
C.
D.
9.如图所示,A、B两小球从相同高度同时水平抛出,经过时间t在空中相遇,若两球的抛出速度都变为原来的2倍,则两球从抛出到相遇经过的时间为( )
A.
B.
C.
D.
10.如图所示,从倾角为的足够长的斜面顶端以速度抛出一个小球,落在斜面上点,小球落在斜面上的速度与斜面的夹角,若把初速度变为,小球仍然落在斜面的情况下,以下说法正确的是( )
A.夹角将变为原来的倍
B.夹角不变
C.空中的运动时间不变
D.小球的水平位移和竖直位移之比变为原来的倍
11.如图所示,斜槽轨道末端切线水平,斜面AB上端位于斜槽轨道末端、下瑞位于水平地面上。一个可视为质点的钢球从斜槽上某处由静止释放,以速度v0从斜槽末端飞出经历时间t落在地面上的D点。把钢球从斜槽上较低位置由静止释放,以速度从斜槽末端飞出落在斜面中点C点。不计空气阻力的作用,则钢球从斜槽末端飞出到落到斜面中点C所经历的时间为( )
A.
B.
C.
D.
12.2020年7月,中国女排在宁波北仑基地进行第二阶段集训,目标是在东京奥运会上完成卫冕。如图所示,排球运动员在发球线正对球网跳起发球,在距地面高度为处使质量的排球(可视为质点)以的初速度水平飞出。不考虑空气阻力,重力加速度取,则排球从被扣出到着地的时间和排球即将着地时的速率分别为(
)
A.
B.
C.
D.
二、多选题
13.如图所示,小球A、B分别从和l的高度水平抛出后落地,上述过程中A、B的水平位移均为,忽略空气阻力,则( )
A.A和B的运动时间相等
B.A的运动时间是B的倍
C.B的初速度是A的2倍
D.A的末速度比B的大
14.如图所示,一小球以某初速度水平抛出,在落地之前经过空中、两点,在点小球速度方向与水平方向的夹角为,在点小球速度方向与水平方向的夹角为,且小球从点运动到点用时。不计空气阻力,取,,取重力加速度大小。下列说法正确的是(
)
A.小球的初速度大小为
B.小球的初速度大小为
C.、两点的高度差为
D.、两点的高度差为
15.如图所示为某次滑雪比赛场地的示意图。运动员从A点滑下,到B点沿斜坡向上,之后从C点飞出,最后落在D点,设运动员在段受到的阻力恒定,不计空气阻力,运动员没有做任何动作,滑板与坡面间的动摩擦因数为0.2,段的倾角为53°,则运动员从B点运动到D点,在水平方向和竖直方向的分速度、随时间t变化关系正确的是(
)
A.
B.
C.
D.
三、实验题
16.图甲是“研究平抛物体运动”的实验装置图,通过描点画出平抛小球的运动轨迹。
(1)以下是实验过程中的一些做法,其中合理的有___________。
A.安装斜槽轨道,其末端是否保持水平不影响实验的研究
B.每次小球释放的初始位置可以任意选择
C.每次小球应从同一高度由静止释放
D.为描出小球的运动轨迹,描绘的点可以用折线连接
(2)实验得到平抛小球的运动轨迹,在轨迹上取一些点,以平抛起点O为坐标原点,测量它们的水平坐标x和竖直坐标y,图乙中y—x2图像能说明平抛小球运动轨迹为抛物线的是___________。
(3)图丙是某同学根据实验画出的平抛小球的运动轨迹,O为平抛的起点,在轨迹上任取两点A、B,测得A、B两点纵坐标y1=5.0
cm,y2=45.0
cm,A、B两点水平间距x=20.0
cm。则平抛小球的初速度v0为___________
m/s。(g取10
m/s2,计算结果保留两位有效数字。)
17.在“探究平抛运动规律”的实验中:
(1)在做“研究平抛运动”的实验时,让小球多次沿同一轨道运动,通过描点法画小球做平抛运动的轨迹,为了能较准确地描绘运动轨迹。下列对实验过程的描述哪些是正确的(______)
A.通过调节使斜槽的末端保持水平
B.每次静止释放小球的位置必须相同
C.小球运动时应与木板上的白纸相接触
D.将球的位置记录在纸上后,取下纸,将点连成平滑曲线
(2)某同学实验时得到了如图所示物体的运动轨迹。O、B、C三点的位置在运动轨迹上已标出,O_______(是或不是)抛出点。
(3)则小球平抛的初速度______。
(4)小球运动到B点的速度vB=________m/s(计算结果均保留两位有效数字)
四、解答题
18.跳台滑雪是勇敢者的运动,它是利用山势特别建造的跳台所进行的。运动员穿专用滑雪板,在助滑路上获得高速后飞出,在空中飞行一段距离后着陆。如图所示,设一位运动员由A点沿水平方向跃起,到B点着陆时,测得AB间距离L=40m,山坡倾角θ=30°(不计空气阻力,g取10m/s2),求:
(1)运动员起跳的速度;
(2)运动员在空中飞行的时间;
(3)运动员经多长时间离坡面距离最大。
19.如图所示,上端开口的圆柱形桶固定在水平地面上,某同学将质量为的小球,从点顺着桶的某条直径方向水平抛出,小球恰好从桶的左侧上边沿进入桶内并打在桶的右下角。已知点到桶左边沿的水平距离,桶的高度,点离地面的高度,桶底和桶壁的厚度均不计,重力加速度大小。求:
(1)小球水平抛出时的速度大小和桶的直径;
(2)为使小球总能落入桶内,则小球从点水平抛出时的速度大小的取值范围。
20.如图所示,一小球自平台上水平抛出,恰好落在台的一倾角为的光滑斜面顶端,并刚好沿光滑斜面下滑,已知斜面顶端与平台的高度差,重力加速度,,,求:
(1)小球水平抛出的初速度是多少?
(2)面顶端与平台边缘的水平距离是多少?
(3)若斜面顶端高,则小球离开平台后经多长时间到达斜面底端?
21.在某项娱乐活动中,要求参与者通过一光滑的斜面将质量为m的物块送上高处的水平传送带后运送到网兜内。斜面长度为l,倾角为θ=,传送带距地面高度为l,传送带的长度为3l,传送带表面的动摩擦因数,传送带一直以速度顺时针运动。当某参与者第一次试操作时瞬间给予小物块一初速度只能将物块刚好送到斜面顶端;第二次调整初速度,恰好让物块水平冲上传送带并成功到达网兜。求:
(1)第一次小物块获得的初速度;
(2)第二次小物块滑上传送带的速度和传送带距斜面的水平距离;
(3)假如小物块是一小煤块,第二次小煤块通过传送带过程中留在传送带上的痕迹长度。
参考答案
1.C
小球离开桌面后做平抛运动,则桌面离地高度为
故选C。
2.D
根据
可得
则AB两球的时间之比为
根据x=vt,则
3.D
AB.平抛运动的落地时间只与竖直高度有关,要使两球在空中相遇必须同时抛出,故AB错误;
CD.因A球在后B球在前,则需要A球的初速度大于B球的初速度,故D正确C错误。
故选D。
4.B
炸弹在空中做平抛运动,炸弹击中目标时竖直分速度
设炸弹击中目标时速度方向与竖直方向的夹角为α,如图所示,则
得α=30°
根据几何关系可知山坡倾角θ=α=30°,故ACD错误,B正确。
故选B。
5.D
AB.苹果在竖直方向做自由落体运动,通过三个窗户的竖直高度相同,竖直方向分速度越来越大,通过第1个窗户时竖直方向的平均速度最小,平均合速度也最小,时间最长,AB错误;
CD.水平方向上,由x=v0t可知,通过第3个窗户的水平位移最小,通过三个窗户的竖直位移相同,则通过第3个窗户的合位移最小,C错误,D正确。
6.C
A.两弹在M、N连线的中点正上方相遇,只能说明末位置相同,不能说明运动轨迹重合,故A错误;
B.由于两弹恰在M、N连线的中点正上方相遇,说明它们的水平位移大小相等,又由于运动的时间相同,所以它们在水平方向上的速度相同,即
v2cosθ=v1
所以
v2>v1
故B错误;
C.两弹都只受到重力,都做匀变速运动,加速度相同,所以拦截弹相对攻击弹做匀速直线运动,故C正确;
D.根据题意只能求出两弹运动时间相同,但不知道拦截炮弹竖直方向初速度的具体值,所以不能判断两弹相遇点距离地面的高度,所以D错误。
7.A
AB.小球做平抛运动,将其分解为水平方向的匀速直线运动,和竖直方向的自由落体运动,则水平方向有
x
=
v0t
竖直方向有
y
=
gt2,vy
=
gt
将小球到达竖直墙面时的速度进行分解,如图所示
由图可知
v0
=
=
=
gtcotθ,v
=
=
A正确、B错误;
C.由选项AB知
x
=
v0t,y
=
gt2
则小球的位移L为
L
=
=
C错误;
D.设小球在时间t内的位移方向与水平方向的夹角为α,则
D错误。
8.A
设速度v与水平方向夹角为θ,则
运动时间
水平位移
联立解得
故选A。
9.C
设第一次抛出时A球的速度为v1,B球的速度为v2,则A、B间的水平距离
第二次抛出时两球的速度为第一次的2倍,但两球间的水平距离不变,则
联立解得
故选C。
10.B
AB.速度与水平方向夹角的正切值
位移与水平方向的正切值
可知速度方向与水平方向夹角正切值是位移与水平方向夹角正切值的2倍。因为位移与水平方向夹角不变,则速度与水平方向夹角不变,所以两个角度之差,即α不变,A错误B正确;
C.根据
解得小球在空中运动时间为
若初速度变为原来的倍,则小球在空中的运动时间变为原来的倍,C错误;
D.小球的水平位移和竖直位移之比
因为若初速度变为原来的倍,小球在空中的运动时间变为原来的倍,则位移之比没有变化,D错误。
11.D
钢球水平飞出至D点运动的时间与运动到B点时间相同,对于落到斜面AB的物体,运动时间满足关系式
其中l为斜面长度,θ为斜面倾角,由此表达式可知
,
12.B
排球飞出后做平抛运动,竖直方向的分运动为自由落体运动,由
代入数据解得
即将着地的竖直速度
即将着地的水平速度
排球即将着地时的速率
13.BD
AB.小球水平抛出后在竖直方向自由下落,A、B分别满足
可解得,,故A错误,B正确;
C.小球在水平方向做匀速直线运动,由
可得A、B的初速度分别为,,故C错误;
D.抛出至落地过程,根据动能定理有
代入数据可解得A、B球落地速度分别为,,可知A的末速度比B的大,D正确。
14.AD
AB.根据速度的分解和竖直方向自由落体运动可知:
,,vBy-vAy=gt
解得小球的初速度大小为,故A正确B错误;
CD.根据以上分析可知,两点竖直速度分别为1.8m/s和3.2m/s。故、两点的高度差
故C错误D正确。
15.BD
AB.运动员在BC部分运动时,受到重力、支持力和斜坡的摩擦力,合力沿斜面向下,所以此时水平方向为匀减速运动,在CD部分运动时,运动员只受重力,做斜抛运动,水平方向为匀速运动,故A错误,B正确;
CD.运动员在BC部分运动时,受到重力、支持力和斜坡的摩擦力,合力沿斜面向下,所以此时竖直方向为匀减速运动,在CD部分运动时,运动员只受重力,做斜抛运动,竖直方向为速度与加速度相反的匀变速运动,故C错误,D正确。
故选BD。
16.C
c
1.0
(1)[1]A.通过调节斜槽使末端保持水平,是为了保证小球做平抛运动,A错误;
BC.为了使每次小球做平抛运动的轨迹相同,就要使小球做平抛运动得初速度相同,故每次都要由静止从同一位置释放,B错误,C正确;
D.由于平抛运动得轨迹是一条抛物线,故应将各点用一条平滑得曲线连接起来,不能用折线,D错误。
故选C。
(2)[2]小球在水平方向做匀速直线运动,水平位移满足
竖直位移满足
联立可得
故y与x2为正比例函数,c正确。
故选c。
(3)[3]设OA过程时间t1,OB过程时间t2,在竖直方向上,由匀变速直线运动公式可得
水平方向由匀速直线运动公式可得
联立代入数据可解得v0=1.0m/s。
17.ABD
不是
2
2.5
(1)[1]A.为了保证小球的初速度水平,需调节斜槽的末端保持水平,A错误;
B.为了保证小球每次做平抛运动的初速度相等,小球每次必须从同一位置由静止释放,B正确;
C.小球做平抛运动时,不应与纸接触,避免摩擦改变运动轨迹,带来误差,C错误;
D.将球的位置记录在纸上后,取下纸,将点连成平滑曲线,并建立坐标,以便分析研究平抛运动,D正确。
故选ABD;
(2)[2]
O到B、B到C过程,水平分位移相等,即时间间隔相等,若O点是抛出点,两段竖直分位移之比应为1:3,而题中竖直分位移之比为1:2,故竖直方向有初速度,O不是抛出点;
(3)[3]竖直方向上,根据
其中t为O到B、B到C过程的时间间隔,可得
水平方向上
(4)[4]设小球经过B点时的竖直分速度为vBy,在竖直方向上有
故
18.(1)
;(2)2s;(3)1s
(1)
(2)运动员在空中飞行时,做平抛运动
,
解得
,
(3)
速度与斜面平行时,离坡面距离最大。有
tanθ==
解得
19.(1)
2m/s
;0.2m;(2)
2m/s~2.5m/s
(1)小球从P点开始到桶的左上边缘时
解得
t1=0.4s
v0=2m/s
小球下落的总时间
则桶的直径
(2)若使小球打到桶右侧上边缘,则
解得
小球从点水平抛出时的速度大小的取值范围为2m/s~2.5m/s.
20.(1);(2);(3)
(1)由题意可知:小球落到斜面上并沿斜面下滑,说明此时小球速度方向与斜面平行,否则小球会弹起,所以
,
代入数据,得
m/s,
(2)由得
水平距离为
(3)小球沿斜面做匀加速直线运动的加速度
,
初速度
且
代入数据,整理得
解得
或(不合题意舍去)
所以
21.(1);(2);(3)
(1)第一次在斜面上滑到顶端时
由运动学公式得
所以第一次小物块获得的初速度
(2)第二次恰好让物块水平冲上传送带,逆向看相当于平抛运动,竖直方向上相当于自由落体,则有
同时
由速度分解关系得第二次小物块滑上传送带的速度
传送带距斜面的水平距离
(3)当物块匀减速至传送带速度相等的时间
物块向右的位移
此过程中传送带向右的位移
划痕长度为相对位移
