空间向量应用
图片预览





文档简介
(共26张PPT)
空间向量应用 三
---立体几何证明中的应用
前段时间我们研究了用空间向量求角(包括线线角、线面角和面面角)、求距离(包括线线距离、点面距离、线面距离和面面距离)
今天我来研究如何利用空间向量来解决立体几何中的有关证明问题。
立体几何中的有关证明问题,大致可分为“平行”“垂直”两大类:
平行:线面平行、面面平行
垂直:线线垂直、线面垂直和面面垂直
平行与垂直的问题的证明,除了要熟悉相关的定理之外,下面几个性质必须掌握。
1、已知b⊥α,a不在α内,如果a⊥b,则a∥α。
2、如果a⊥α, a⊥β,则α∥β。
3、如果a∥b, a⊥α,则b⊥α。(课本P22.6)
4、如果a⊥α, b⊥β, a⊥b,则α⊥β。
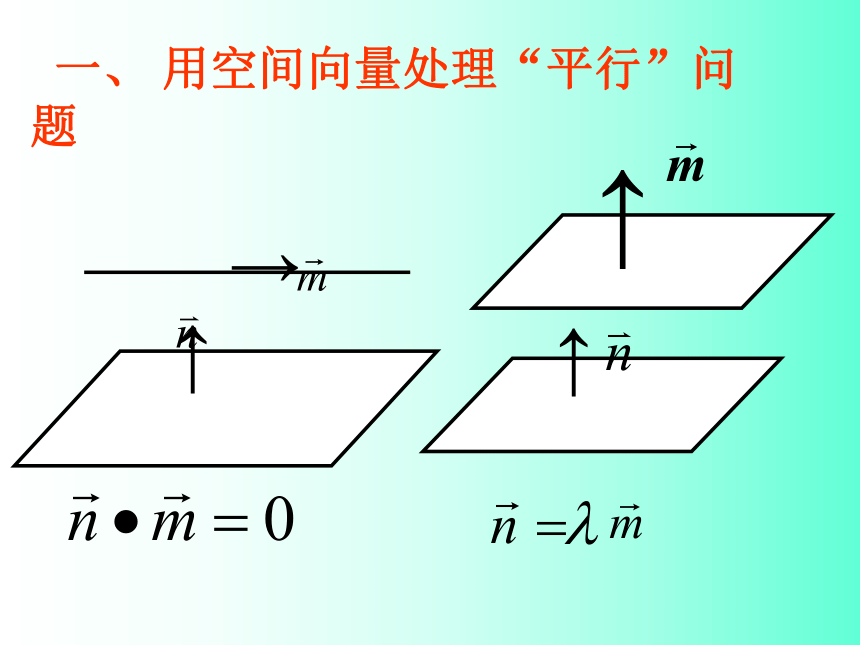
一、 用空间向量处理“平行”问题
一、 用空间向量处理“平行”问题
↑
→
↑
↑
G
A
E
D
C
B
F
H
M
N
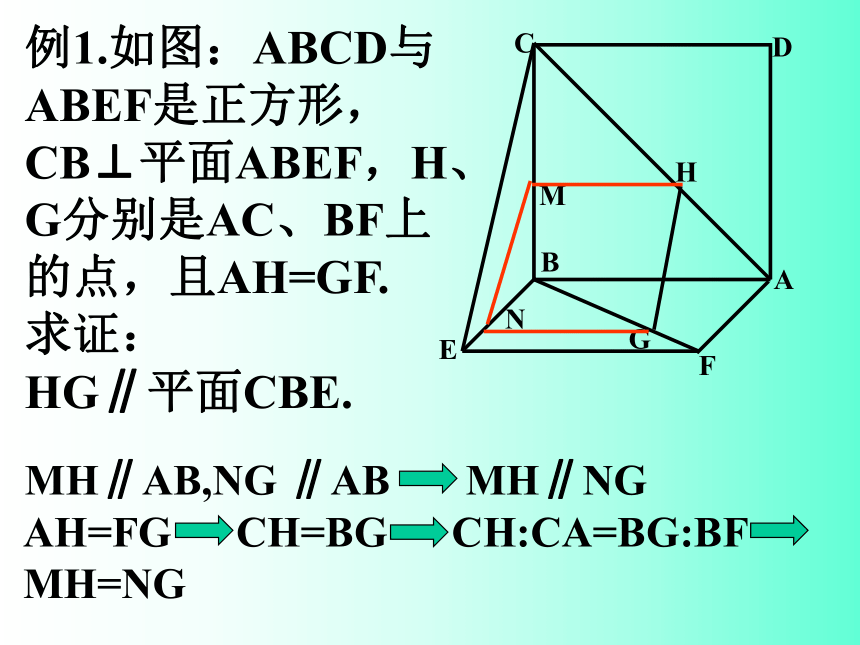
例1.如图:ABCD与ABEF是正方形,CB⊥平面ABEF,H、G分别是AC、BF上的点,且AH=GF. 求证: HG∥平面CBE.
MH∥AB,NG ∥AB MH∥NG
AH=FG CH=BG CH:CA=BG:BF MH=NG
G
A
E
D
C
B
F
H
P
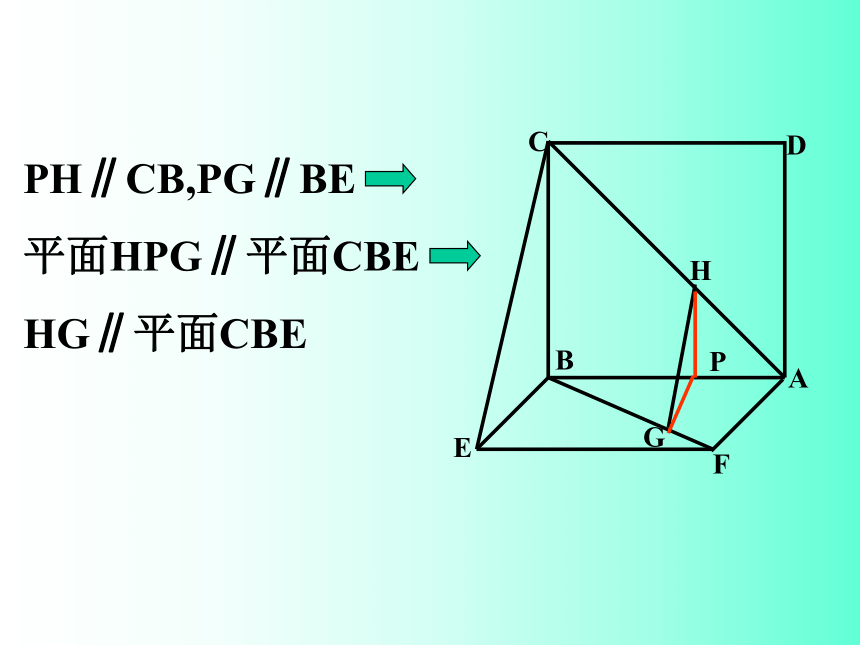
PH∥CB,PG∥BE
平面HPG∥平面CBE
HG∥平面CBE
G
A
E
D
C
B
F
H
o
z
y
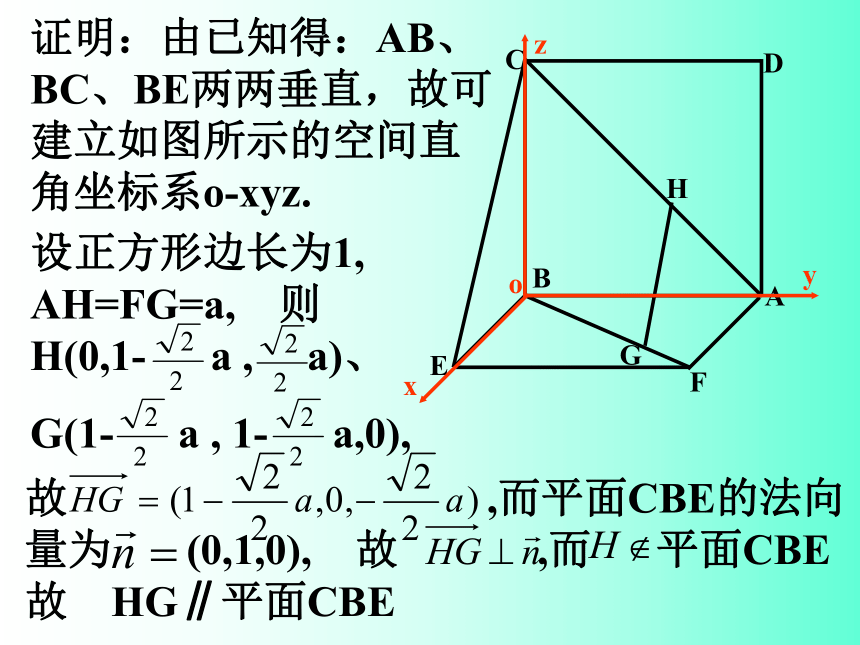
证明:由已知得:AB、BC、BE两两垂直,故可建立如图所示的空间直角坐标系o-xyz.
x
设正方形边长为1, AH=FG=a, 则H(0,1- a , a)、
G(1- a , 1- a,0),
故 ,而平面CBE的法向量为 (0,1,0), 故 ,而 平面CBE 故 HG∥平面CBE
R
D
B
C
A
A1
Q
P
N
M
D1
C1
B1
例2.在正方体ABCD-A1B1C1D1中,P、Q分别是A1B1和BC上的动点,且A1P=BQ,M是AB1的中点,N是PQ的中点. 求证: MN∥平面AC.
M是中点,N是中点 MN∥RQ
MN∥平面AC
D
B
C
A
A1
Q
P
N
M
D1
C1
B1
作PP1⊥AB于P1,作MM1 ⊥AB于M1,连结QP1, 作NN1⊥ QP1于N1,连结M1N1
N1
M1
P1
NN1∥PP1 MM1∥AA1
又NN1、MM1均等于边长的一半
故MM1N1N是平行四边形,故MN∥M1N1
MN∥平面AC
D
B
C
A
A1
Q
P
N
M
D1
C1
B1
z
y
x
o
证明:建立如图所示的空间直角坐标系o-xyz
设正方形边长为2,又A1P=BQ=2x
则P(2,2x,2)、Q(2-2x,2,0) 故N(2-x, 1+x, 1),而M(2, 1, 1)
所以向量 (-x, x, 0),又平面AC的法向量为 (0, 0, 1),∴ ∴
又M不在平面AC 内,所以MN∥平面AC
D
C
B
A
D1
C1
B1
A1
例3.在正方体ABCD-A1B1C1D1中,求证: 平面A1BD∥平面CB1D1
平行四边形A1BCD1
A1B∥D1C
平行四边形DBB1D1
B1D1∥BD
于是平面A1BD∥平面CB1D1
D
C
B
A
D1
C1
B1
A1
o
z
y
x
证明:建立如图所示的空间直角坐标系o-xyz
设正方形边长为1,则向量
设平面BDA1的法向量为
则有
x+z=0
x+y=0
令x=1,则得方程组的解为
x=1 y=-1 z=-1
故平面BDA1的法向量为
同理可得平面CB1D1的法向量为
则显然有
即得两平面BDA1和CB1D1的法向量平行
所以 平面BDA1∥CB1D1
通过本例的练习,同学们要进一步掌握平面法向量的求法:即用平面内的两个相交向量与假设的法向量求数量积等于0,利用解方程组的方法求出平面法向量(在解的过程中可令其中一个未知数为某个数)。
※例1、2与例3在利用法向量时有何不同?
D
C
B
A
D1
C1
B1
A1
F
G
H
E
例4.在正方体ABCD-A1B1C1D1中,E、F、G、H分别是A1B1、B1C1、C1D1、D1A1的中点. 求证: 平面AEH∥平面BDGF
AD∥GF,AD=GF
又EH∥B1D1,GF∥B1D1 EH∥GF
平行四边形ADGE AE∥DG
故得平面AEH∥平面BDGF
D
C
B
A
D1
C1
B1
A1
H
G
F
E
o
z
y
x
略证:建立如图所示的空间直角坐标系o-xyz
则求得平面AEF的法向量为
求得平面BDGH的法向量为
显然有
故 平面AEH∥平面BDGF
二、 用空间向量处理“垂直”问题
二、 用空间向量处理“垂直”问题
↑
F
E
X
Y
Z
证明:
分别以 为坐标向量建立空间直角坐标系
例6:如图,在正三棱柱ABC-A1B1C1中,AB=AA1/3=a,E、F分别是BB1、CC1上的点,且BE=a,CF=2a 。求证:面AEF 面ACF。
A
F
E
C1
B1
A1
C
B
x
z
y
A
F
E
C1
B1
A1
C
B
z
y
不防设 a =2,则A(0,0,0),B( 3 ,1,0),C(0,2,0),E( 3,1,2) ,F(0,2,4),AE=( 3,1,2)AF=(0,2,4),因为,x轴 面ACF,所以可取面ACF的法向量为m=(1,0,0),设n=(x,y,z)是面AEF的法向量,则
x
{
nAE= 3x+y+2z=0
nAF=2y+4z=0
{
x=0
y= -2z
令z=1得, n=(0,-2,1)
显然有m n=0,即,m n
面AEF 面ACF
证明:如图,建立空间直角坐标系A-xyz ,
A
D
C
B
⑴求证:平面MNC⊥平面PBC;
⑵求点A到平面MNC的距离。
已知ABCD是矩形,PD⊥平面ABCD,PD=DC=a,AD= ,M、N分别是AD、PB的中点。
P
M
N
练习1
小结:
利用向量的有关知识解决一些立体几何的问题,是近年来很“热”的话题,其原因是它把有关的“证明”转化为“程序化的计算” 。本课时讲的内容是立体几何中的证明“线面平行、垂直”的一些例子,结合我们以前讲述立体几何的其他问题(如:求角、求距离等),大家从中可以进一步看出基中一些解题的“套路”。
利用向量解题 的关键是建立适当的空间直角坐标系及写出有关点的坐标。
用代数的方法解决立体几何问题是立体几何的发展趋势,而向量是用代数的方法解决立体几何问题的主要工具,故学会用向量法解立体几何问题是学好立体几何的基础。
空间向量应用 三
---立体几何证明中的应用
前段时间我们研究了用空间向量求角(包括线线角、线面角和面面角)、求距离(包括线线距离、点面距离、线面距离和面面距离)
今天我来研究如何利用空间向量来解决立体几何中的有关证明问题。
立体几何中的有关证明问题,大致可分为“平行”“垂直”两大类:
平行:线面平行、面面平行
垂直:线线垂直、线面垂直和面面垂直
平行与垂直的问题的证明,除了要熟悉相关的定理之外,下面几个性质必须掌握。
1、已知b⊥α,a不在α内,如果a⊥b,则a∥α。
2、如果a⊥α, a⊥β,则α∥β。
3、如果a∥b, a⊥α,则b⊥α。(课本P22.6)
4、如果a⊥α, b⊥β, a⊥b,则α⊥β。
一、 用空间向量处理“平行”问题
一、 用空间向量处理“平行”问题
↑
→
↑
↑
G
A
E
D
C
B
F
H
M
N
例1.如图:ABCD与ABEF是正方形,CB⊥平面ABEF,H、G分别是AC、BF上的点,且AH=GF. 求证: HG∥平面CBE.
MH∥AB,NG ∥AB MH∥NG
AH=FG CH=BG CH:CA=BG:BF MH=NG
G
A
E
D
C
B
F
H
P
PH∥CB,PG∥BE
平面HPG∥平面CBE
HG∥平面CBE
G
A
E
D
C
B
F
H
o
z
y
证明:由已知得:AB、BC、BE两两垂直,故可建立如图所示的空间直角坐标系o-xyz.
x
设正方形边长为1, AH=FG=a, 则H(0,1- a , a)、
G(1- a , 1- a,0),
故 ,而平面CBE的法向量为 (0,1,0), 故 ,而 平面CBE 故 HG∥平面CBE
R
D
B
C
A
A1
Q
P
N
M
D1
C1
B1
例2.在正方体ABCD-A1B1C1D1中,P、Q分别是A1B1和BC上的动点,且A1P=BQ,M是AB1的中点,N是PQ的中点. 求证: MN∥平面AC.
M是中点,N是中点 MN∥RQ
MN∥平面AC
D
B
C
A
A1
Q
P
N
M
D1
C1
B1
作PP1⊥AB于P1,作MM1 ⊥AB于M1,连结QP1, 作NN1⊥ QP1于N1,连结M1N1
N1
M1
P1
NN1∥PP1 MM1∥AA1
又NN1、MM1均等于边长的一半
故MM1N1N是平行四边形,故MN∥M1N1
MN∥平面AC
D
B
C
A
A1
Q
P
N
M
D1
C1
B1
z
y
x
o
证明:建立如图所示的空间直角坐标系o-xyz
设正方形边长为2,又A1P=BQ=2x
则P(2,2x,2)、Q(2-2x,2,0) 故N(2-x, 1+x, 1),而M(2, 1, 1)
所以向量 (-x, x, 0),又平面AC的法向量为 (0, 0, 1),∴ ∴
又M不在平面AC 内,所以MN∥平面AC
D
C
B
A
D1
C1
B1
A1
例3.在正方体ABCD-A1B1C1D1中,求证: 平面A1BD∥平面CB1D1
平行四边形A1BCD1
A1B∥D1C
平行四边形DBB1D1
B1D1∥BD
于是平面A1BD∥平面CB1D1
D
C
B
A
D1
C1
B1
A1
o
z
y
x
证明:建立如图所示的空间直角坐标系o-xyz
设正方形边长为1,则向量
设平面BDA1的法向量为
则有
x+z=0
x+y=0
令x=1,则得方程组的解为
x=1 y=-1 z=-1
故平面BDA1的法向量为
同理可得平面CB1D1的法向量为
则显然有
即得两平面BDA1和CB1D1的法向量平行
所以 平面BDA1∥CB1D1
通过本例的练习,同学们要进一步掌握平面法向量的求法:即用平面内的两个相交向量与假设的法向量求数量积等于0,利用解方程组的方法求出平面法向量(在解的过程中可令其中一个未知数为某个数)。
※例1、2与例3在利用法向量时有何不同?
D
C
B
A
D1
C1
B1
A1
F
G
H
E
例4.在正方体ABCD-A1B1C1D1中,E、F、G、H分别是A1B1、B1C1、C1D1、D1A1的中点. 求证: 平面AEH∥平面BDGF
AD∥GF,AD=GF
又EH∥B1D1,GF∥B1D1 EH∥GF
平行四边形ADGE AE∥DG
故得平面AEH∥平面BDGF
D
C
B
A
D1
C1
B1
A1
H
G
F
E
o
z
y
x
略证:建立如图所示的空间直角坐标系o-xyz
则求得平面AEF的法向量为
求得平面BDGH的法向量为
显然有
故 平面AEH∥平面BDGF
二、 用空间向量处理“垂直”问题
二、 用空间向量处理“垂直”问题
↑
F
E
X
Y
Z
证明:
分别以 为坐标向量建立空间直角坐标系
例6:如图,在正三棱柱ABC-A1B1C1中,AB=AA1/3=a,E、F分别是BB1、CC1上的点,且BE=a,CF=2a 。求证:面AEF 面ACF。
A
F
E
C1
B1
A1
C
B
x
z
y
A
F
E
C1
B1
A1
C
B
z
y
不防设 a =2,则A(0,0,0),B( 3 ,1,0),C(0,2,0),E( 3,1,2) ,F(0,2,4),AE=( 3,1,2)AF=(0,2,4),因为,x轴 面ACF,所以可取面ACF的法向量为m=(1,0,0),设n=(x,y,z)是面AEF的法向量,则
x
{
nAE= 3x+y+2z=0
nAF=2y+4z=0
{
x=0
y= -2z
令z=1得, n=(0,-2,1)
显然有m n=0,即,m n
面AEF 面ACF
证明:如图,建立空间直角坐标系A-xyz ,
A
D
C
B
⑴求证:平面MNC⊥平面PBC;
⑵求点A到平面MNC的距离。
已知ABCD是矩形,PD⊥平面ABCD,PD=DC=a,AD= ,M、N分别是AD、PB的中点。
P
M
N
练习1
小结:
利用向量的有关知识解决一些立体几何的问题,是近年来很“热”的话题,其原因是它把有关的“证明”转化为“程序化的计算” 。本课时讲的内容是立体几何中的证明“线面平行、垂直”的一些例子,结合我们以前讲述立体几何的其他问题(如:求角、求距离等),大家从中可以进一步看出基中一些解题的“套路”。
利用向量解题 的关键是建立适当的空间直角坐标系及写出有关点的坐标。
用代数的方法解决立体几何问题是立体几何的发展趋势,而向量是用代数的方法解决立体几何问题的主要工具,故学会用向量法解立体几何问题是学好立体几何的基础。
