5.3平行线的性质-2020-2021学年人教版七年级数学下册导学案(Word版含答案)
文档属性
| 名称 | 5.3平行线的性质-2020-2021学年人教版七年级数学下册导学案(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 506.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 10:27:11 | ||
图片预览



文档简介
5.3平行线的性质
【总结解题方法 提升解题能力】
【知识点梳理】 一、平行线的性质
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
二、命题、定理、证明
1.命题:判断一件事情的语句,叫做命题.
【要点诠释】
(1)命题的结构:每个命题都由题设、结论两部分组成,题设是已知事项,结论是由已知事项推出的事项.
(2)命题的表达形式:“如果……,那么…….”,也可写成:“若……,则…….”
(3)真命题与假命题:
真命题:题设成立结论一定成立的命题,叫做真命题.
假命题:题设成立而不能保证结论一定成立的命题,叫做假命题.
2.定理:定理是从真命题(公理或其他已被证明的定理)出发,经过推理证实得到的另一个真命题,定理也可以作为继续推理的依据.
3.证明:在很多情况下,一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做证明.
一、平行线的性质
1、如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )。
A、65° B、115° C、125° D、130°
2、如图,直线∥,∠1=70°,∠2=30°,则∠A的度数是( )。
A、30° B、 35° C、40° D、50°
3、如图所示,已知a∥b∥c,∠1=105°,∠2=140°,则∠3的度数是( )。
A、75° B、65° C、55° D、50°
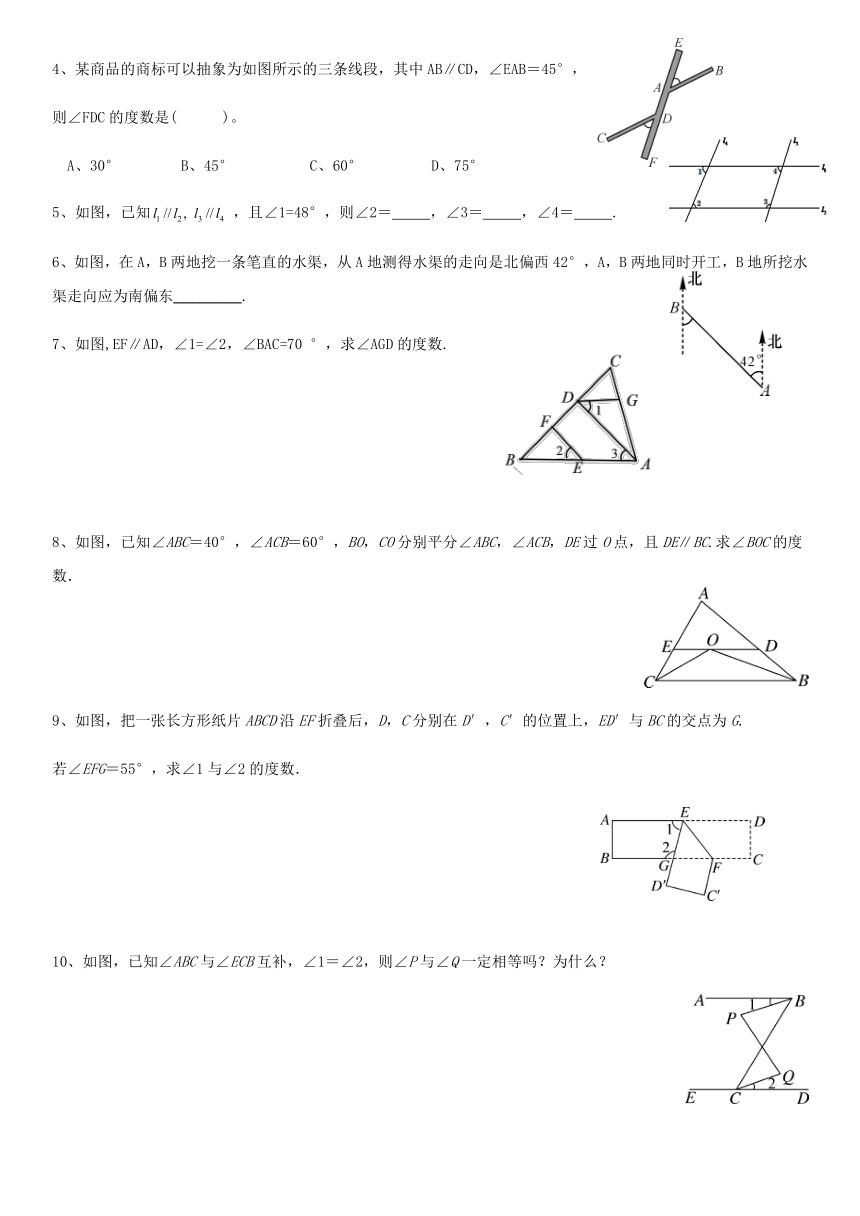
4、某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,
则∠FDC的度数是( )。
A、30° B、45° C、60° D、75°
5、如图,已知,且∠1=48°,则∠2= ,∠3= ,∠4= .
6、如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东_________.
7、如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.
8、如图,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC.求∠BOC的度数.
9、如图,把一张长方形纸片ABCD沿EF折叠后,D,C分别在D′,C′的位置上,ED′与BC的交点为G.
若∠EFG=55°,求∠1与∠2的度数.
10、如图,已知∠ABC与∠ECB互补,∠1=∠2,则∠P与∠Q一定相等吗?为什么?
二、命题、定理、证明
1、下列语句中,是命题的是( )。
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A.①④⑤ B.①②④ C.①②⑤ D.②③④⑤
2、下列命题:①若|a|>|b|,那么a2>b2;②两点之间,线段最短;③对顶角相等;④内错角相等.其中真命题的个数是( )。
A.1个 B.2个 C.3个 D.4个
3、把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是_____________________________.
4、判断下列命题的真假,是假命题的举出反例。
①两个锐角的和是钝角;
②一个角的补角大于这个角;
③不相等的角不是对顶角.
5、把下列命题写成“如果……那么……”的形式,并判断其真假.
(1)等角的补角相等;
(2)不相等的角不是对顶角;
(3)相等的角是内错角.
6、如图,BD平分∠ABC,若∠BCD=70°,∠ABD=55°.求证:CD∥AB.
【巩固练习】
一、选择题。
1、如图,若,则下列结论一定成立的是( )。
A. B.
C. D.
2、如图,将三角板的直角顶点放在直尺的一边上,若,则的度数为( )。
A. B. C. D.
3、下列语句:①三角形的内角和是180°;②作一个角等于一个已知角;③两条直线被第三条直线所截,同位角相等;④延长线段AB到C,使BC=AB,其中是命题的有( )。
A.①② B.②③ C.①④ D.①③
4、下列命题中,是真命题的是( )。
A.互补的角是邻补角 B.相等的角是对顶角
C.内错角相等 D.对顶角都相等
5、如图,已知AB∥CD∥EF,则∠x、∠y、∠z三者之间的关系是( )。
A. B.
C. D.
二、填空题。
6、如下图,AB∥CD,直线l分别交AB、CD于E,F,∠1=56°,则∠2的度数是________°.
7、如下图,a∥b,AC分别交直线a、b于点B、C,,若,则__________度.
8、如下图,AB∥CD,∠B=115°,∠C=45°,则∠BEC=__________.
第6题 第7题 第8题 第9题
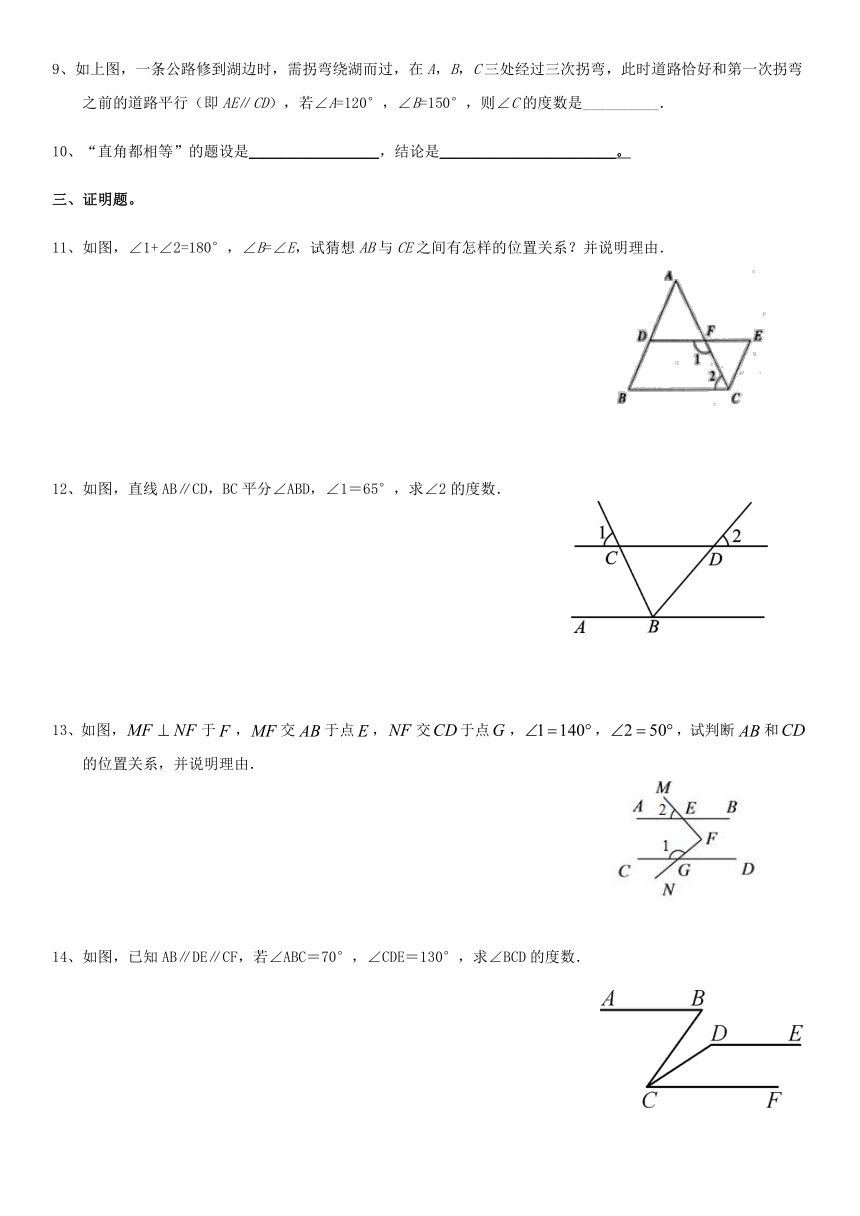
9、如上图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是__________.
10、“直角都相等”的题设是_________________,结论是_______________________。
三、证明题。
11、如图,∠1+∠2=180°,∠B=∠E,试猜想AB与CE之间有怎样的位置关系?并说明理由.
12、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
13、如图,于,交于点,交于点,,,试判断和的位置关系,并说明理由.
14、如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
15、阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
答 案
一、平行线的性质
1、如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( B )。
A、65° B、115° C、125° D、130°
2、如图,直线∥,∠1=70°,∠2=30°,则∠A的度数是( C )。
A、30° B、 35° C、40° D、50°
3、如图所示,已知a∥b∥c,∠1=105°,∠2=140°,则∠3的度数是( B )。
A、75° B、65° C、55° D、50°
4、某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,
则∠FDC的度数是( B )。
A、30° B、45° C、60° D、75°
5、如图,已知,且∠1=48°,则∠2= 48°,∠3= 132°,∠4= 48°.
6、如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东__42°__.
7、如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.
解:∵EF∥AD;∴∠2=∠3(两直线平行,同位角相等)
∵∠1=∠2;∴∠1=∠3(等量代换)
∴AB∥DG(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
∵∠BAC=70 °;∴∠AGD=180°-70°=110°
8、如图,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC.求∠BOC的度数.
解:∵CO平分∠ACB,∴∠OCB=∠ACB=×60°=30°.
同理得∠OBC=20°.∵DE∥BC,∴∠EOC=∠OCB=30°,∠DOB=∠OBC=20°,
∴∠BOC=180°-∠DOB-∠EOC=180°-20°-30°=130°.
9、如图,把一张长方形纸片ABCD沿EF折叠后,D,C分别在D′,C′的位置上,ED′与BC的交点为G.
若∠EFG=55°,求∠1与∠2的度数.
解:∵AD∥BC,∴∠DEF=∠EFG=55°.
由折叠可知∠GEF=∠DEF=55°,∴∠1=180°-2×55°=70°.
∵AD∥BC,∴∠2=180°-∠1=110°.
10、如图,已知∠ABC与∠ECB互补,∠1=∠2,则∠P与∠Q一定相等吗?为什么?
解:∠P=∠Q.
理由如下:∵∠ABC+∠ECB=180°,∴AB∥ED,∴∠ABC=∠BCD.
∵∠1=∠2,∴∠ABC-∠1=∠BCD-∠2,
即∠PBC=∠BCQ,∴PB∥CQ,∴∠P=∠Q.
二、命题、定理、证明
1、下列语句中,是命题的是( A )。
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A.①④⑤ B.①②④ C.①②⑤ D.②③④⑤
2、下列命题:①若|a|>|b|,那么a2>b2;②两点之间,线段最短;③对顶角相等;④内错角相等.其中真命题的个数是( C )。
A.1个 B.2个 C.3个 D.4个
3、把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是如果两条直线垂直于同一条直线,那么这两条直线平行.
4、判断下列命题的真假,是假命题的举出反例。
①两个锐角的和是钝角;②一个角的补角大于这个角;③不相等的角不是对顶角.
解:①假命题.反例为:30°与40°的和为70°.
②假命题.反例为:120°的补角为60°.
③真命题.
5、把下列命题写成“如果……那么……”的形式,并判断其真假.
(1)等角的补角相等;
(2)不相等的角不是对顶角;
(3)相等的角是内错角.
解:(1)如果两个角是两个相等的角的补角,那么这两个角相等.是真命题.
(2)如果两个角不相等,那么这两个角不是对顶角.是真命题.
(3)如果两个角相等,那么这两个角是内错角.是假命题.
6、如图,BD平分∠ABC,若∠BCD=70°,∠ABD=55°.求证:CD∥AB.
证明:∵BD平分∠ABC,∠ABD=55°,
∴∠ABC=2∠ABD=110°.
又∵∠BCD=70°,
∴∠ABC+∠BCD=180°. ∴CD∥AB.
【巩固练习】
一、选择题。
1、如图,若,则下列结论一定成立的是( )。
A. B.
C. D.
【答案】D;【解析】因为∠1=∠3,所以AD∥BC,所以∠1+∠2=180°,故选D.
2、如图,将三角板的直角顶点放在直尺的一边上,若,则的度数为( )。
A. B. C. D.
【答案】C
【解析】如图,因为AD∥BC,所以∠1=∠3=65°,因为∠2+∠3+90°=180°,所以∠2=90°-∠3=90°-65°=25°,故选C.
3、下列语句:①三角形的内角和是180°;②作一个角等于一个已知角;③两条直线被第三条直线所截,同位角相等;④延长线段AB到C,使BC=AB,其中是命题的有( )。
A.①② B.②③ C.①④ D.①③
【答案】D
【解析】①三角形的内角和是180°,是命题;②作一个角等于一个已知角,不是命题;③两条直线被第三条直线所截,同位角相等,是命题;④延长线段AB到C,使BC=AB,不是命题,故选D.
4、下列命题中,是真命题的是( )。
A.互补的角是邻补角 B.相等的角是对顶角
C.内错角相等 D.对顶角都相等
【答案】D
【解析】A、两直线平行时,同旁内角互补,此时这一对同旁内角不是邻补角,故本选项错误;
B、等腰三角形的两个底角相等,此时这两个底角不是对顶角,故本选项错误;
C、只有两直线平行时,内错角才相等,故本选项错误;?
D、对顶角都相等,故本选项正确.?
故选D.
5、如图,已知AB∥CD∥EF,则∠x、∠y、∠z三者之间的关系是( )。
A. B.
C. D.
【答案】B;【解析】∵∠y+∠CEF=180°,∠CEF=∠x—∠z,∴∠X+∠Y—∠Z=180°,故选B。
二、填空题。
6、如图,AB∥CD,直线l分别交AB、CD于E,F,∠1=56°,则∠2的度数是________°.
【答案】124
【解析】∵∠1=56°,∴∠3=180°?∠1=124°,∵AB∥CD,∴∠2=∠3=124°.
故答案为:124.
7、如图,a∥b,AC分别交直线a、b于点B、C,,若,则__________度.
【答案】65
【解析】∵AC⊥DC,∴∠1+∠3=90°,∵∠1=25°,∴∠3=90°-∠1=90°-25°=65°,
∵a∥b,∴∠2=∠1=65°,故答案为:65.
8、如图,AB∥CD,∠B=115°,∠C=45°,则∠BEC=__________.
【答案】110°
【解析】如图,过点E作EF∥AB.因为AB∥CD,所以EF∥CD,所以∠B+∠BEF=180°,∠C=∠CEF.
因为∠B=115°,∠C=45°,所以∠BEF=180°-115°=65°,∠CEF=45°,所以∠BEC=∠BEF+∠CEF=65°+45°=110°,故答案为:110°.
9、如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是__________.
【答案】150°
【解析】如图,过点B作BG∥AE,∵AE∥CD,∴AE∥BG∥CD。
∴∠A=∠2,∠1+∠C=180°,∵∠A=120°,∴∠2=120°,∴∠1=150°—120°=30°,
∴∠C=180°—30°=150°,故答案为:150°。
10、“直角都相等”的题设是两个角是直角,结论是这两个角相等.
三、证明题。
11、如图,∠1+∠2=180°,∠B=∠E,试猜想AB与CE之间有怎样的位置关系?并说明理由.
【解析】AB∥CE,理由如下:
∵∠1+∠2=180°,
∴DE∥BC(同旁内角互补,两直线平行),
∴∠ADF=∠B(两直线平行,同位角相等),
∵∠B=∠E,
∴∠ADF=∠E,∴AB∥CE(内错角相等,两直线平行).
12、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
解:∵直线AB∥CD,∠1=65°,
∴∠ABC=∠1=65°.
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°.
∵直线AB∥CD,∴∠ABD+∠BDC=180°.
∴∠2=∠BDC=180°-∠ABD=180°-130°=50°.
13、如图,于,交于点,交于点,,,试判断和的位置关系,并说明理由.
【解析】如图,过点作.
∵,∴(两直线平行,同位角相等).
∵(已知),∴(等量代换).
∵(已知),∴(垂直的定义),
∴.
∵,∴,
∴(同旁内角互补,两直线平行),
∴(平行于同一条直线的两条直线互相平行).
14、如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°.
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°.∴∠DCF=50°.
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
15、阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
解:过点P作PE∥AB.
∵AB∥CD,∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
解:如图乙,过点P作PE∥AB.
∵AB∥CD(已知),
∴PE∥AB∥CD(平行于同一直线的两条直线平行).
∴∠A=∠EPA,∠EPC=∠C(两直线平行,内错角相等).
∵∠APC=∠EPA+∠EPC,
∴∠APC=∠A+∠C(等量代换).
如图丙,过点P作PF∥AB.
∴∠FPA=∠A(两直线平行,内错角相等).
∵AB∥CD(已知),∴PF∥CD(平行于同一直线的两条直线平行).
∴∠FPC=∠C(两直线平行,内错角相等).
∵∠FPC-∠FPA=∠APC,
∴∠C-∠A=∠APC(等量代换).
【总结解题方法 提升解题能力】
【知识点梳理】 一、平行线的性质
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
二、命题、定理、证明
1.命题:判断一件事情的语句,叫做命题.
【要点诠释】
(1)命题的结构:每个命题都由题设、结论两部分组成,题设是已知事项,结论是由已知事项推出的事项.
(2)命题的表达形式:“如果……,那么…….”,也可写成:“若……,则…….”
(3)真命题与假命题:
真命题:题设成立结论一定成立的命题,叫做真命题.
假命题:题设成立而不能保证结论一定成立的命题,叫做假命题.
2.定理:定理是从真命题(公理或其他已被证明的定理)出发,经过推理证实得到的另一个真命题,定理也可以作为继续推理的依据.
3.证明:在很多情况下,一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做证明.
一、平行线的性质
1、如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( )。
A、65° B、115° C、125° D、130°
2、如图,直线∥,∠1=70°,∠2=30°,则∠A的度数是( )。
A、30° B、 35° C、40° D、50°
3、如图所示,已知a∥b∥c,∠1=105°,∠2=140°,则∠3的度数是( )。
A、75° B、65° C、55° D、50°
4、某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,
则∠FDC的度数是( )。
A、30° B、45° C、60° D、75°
5、如图,已知,且∠1=48°,则∠2= ,∠3= ,∠4= .
6、如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东_________.
7、如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.
8、如图,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC.求∠BOC的度数.
9、如图,把一张长方形纸片ABCD沿EF折叠后,D,C分别在D′,C′的位置上,ED′与BC的交点为G.
若∠EFG=55°,求∠1与∠2的度数.
10、如图,已知∠ABC与∠ECB互补,∠1=∠2,则∠P与∠Q一定相等吗?为什么?
二、命题、定理、证明
1、下列语句中,是命题的是( )。
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A.①④⑤ B.①②④ C.①②⑤ D.②③④⑤
2、下列命题:①若|a|>|b|,那么a2>b2;②两点之间,线段最短;③对顶角相等;④内错角相等.其中真命题的个数是( )。
A.1个 B.2个 C.3个 D.4个
3、把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是_____________________________.
4、判断下列命题的真假,是假命题的举出反例。
①两个锐角的和是钝角;
②一个角的补角大于这个角;
③不相等的角不是对顶角.
5、把下列命题写成“如果……那么……”的形式,并判断其真假.
(1)等角的补角相等;
(2)不相等的角不是对顶角;
(3)相等的角是内错角.
6、如图,BD平分∠ABC,若∠BCD=70°,∠ABD=55°.求证:CD∥AB.
【巩固练习】
一、选择题。
1、如图,若,则下列结论一定成立的是( )。
A. B.
C. D.
2、如图,将三角板的直角顶点放在直尺的一边上,若,则的度数为( )。
A. B. C. D.
3、下列语句:①三角形的内角和是180°;②作一个角等于一个已知角;③两条直线被第三条直线所截,同位角相等;④延长线段AB到C,使BC=AB,其中是命题的有( )。
A.①② B.②③ C.①④ D.①③
4、下列命题中,是真命题的是( )。
A.互补的角是邻补角 B.相等的角是对顶角
C.内错角相等 D.对顶角都相等
5、如图,已知AB∥CD∥EF,则∠x、∠y、∠z三者之间的关系是( )。
A. B.
C. D.
二、填空题。
6、如下图,AB∥CD,直线l分别交AB、CD于E,F,∠1=56°,则∠2的度数是________°.
7、如下图,a∥b,AC分别交直线a、b于点B、C,,若,则__________度.
8、如下图,AB∥CD,∠B=115°,∠C=45°,则∠BEC=__________.
第6题 第7题 第8题 第9题
9、如上图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是__________.
10、“直角都相等”的题设是_________________,结论是_______________________。
三、证明题。
11、如图,∠1+∠2=180°,∠B=∠E,试猜想AB与CE之间有怎样的位置关系?并说明理由.
12、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
13、如图,于,交于点,交于点,,,试判断和的位置关系,并说明理由.
14、如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
15、阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
答 案
一、平行线的性质
1、如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED=( B )。
A、65° B、115° C、125° D、130°
2、如图,直线∥,∠1=70°,∠2=30°,则∠A的度数是( C )。
A、30° B、 35° C、40° D、50°
3、如图所示,已知a∥b∥c,∠1=105°,∠2=140°,则∠3的度数是( B )。
A、75° B、65° C、55° D、50°
4、某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,
则∠FDC的度数是( B )。
A、30° B、45° C、60° D、75°
5、如图,已知,且∠1=48°,则∠2= 48°,∠3= 132°,∠4= 48°.
6、如图,在A,B两地挖一条笔直的水渠,从A地测得水渠的走向是北偏西42°,A,B两地同时开工,B地所挖水渠走向应为南偏东__42°__.
7、如图,EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数.
解:∵EF∥AD;∴∠2=∠3(两直线平行,同位角相等)
∵∠1=∠2;∴∠1=∠3(等量代换)
∴AB∥DG(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
∵∠BAC=70 °;∴∠AGD=180°-70°=110°
8、如图,已知∠ABC=40°,∠ACB=60°,BO,CO分别平分∠ABC,∠ACB,DE过O点,且DE∥BC.求∠BOC的度数.
解:∵CO平分∠ACB,∴∠OCB=∠ACB=×60°=30°.
同理得∠OBC=20°.∵DE∥BC,∴∠EOC=∠OCB=30°,∠DOB=∠OBC=20°,
∴∠BOC=180°-∠DOB-∠EOC=180°-20°-30°=130°.
9、如图,把一张长方形纸片ABCD沿EF折叠后,D,C分别在D′,C′的位置上,ED′与BC的交点为G.
若∠EFG=55°,求∠1与∠2的度数.
解:∵AD∥BC,∴∠DEF=∠EFG=55°.
由折叠可知∠GEF=∠DEF=55°,∴∠1=180°-2×55°=70°.
∵AD∥BC,∴∠2=180°-∠1=110°.
10、如图,已知∠ABC与∠ECB互补,∠1=∠2,则∠P与∠Q一定相等吗?为什么?
解:∠P=∠Q.
理由如下:∵∠ABC+∠ECB=180°,∴AB∥ED,∴∠ABC=∠BCD.
∵∠1=∠2,∴∠ABC-∠1=∠BCD-∠2,
即∠PBC=∠BCQ,∴PB∥CQ,∴∠P=∠Q.
二、命题、定理、证明
1、下列语句中,是命题的是( A )。
①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A.①④⑤ B.①②④ C.①②⑤ D.②③④⑤
2、下列命题:①若|a|>|b|,那么a2>b2;②两点之间,线段最短;③对顶角相等;④内错角相等.其中真命题的个数是( C )。
A.1个 B.2个 C.3个 D.4个
3、把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是如果两条直线垂直于同一条直线,那么这两条直线平行.
4、判断下列命题的真假,是假命题的举出反例。
①两个锐角的和是钝角;②一个角的补角大于这个角;③不相等的角不是对顶角.
解:①假命题.反例为:30°与40°的和为70°.
②假命题.反例为:120°的补角为60°.
③真命题.
5、把下列命题写成“如果……那么……”的形式,并判断其真假.
(1)等角的补角相等;
(2)不相等的角不是对顶角;
(3)相等的角是内错角.
解:(1)如果两个角是两个相等的角的补角,那么这两个角相等.是真命题.
(2)如果两个角不相等,那么这两个角不是对顶角.是真命题.
(3)如果两个角相等,那么这两个角是内错角.是假命题.
6、如图,BD平分∠ABC,若∠BCD=70°,∠ABD=55°.求证:CD∥AB.
证明:∵BD平分∠ABC,∠ABD=55°,
∴∠ABC=2∠ABD=110°.
又∵∠BCD=70°,
∴∠ABC+∠BCD=180°. ∴CD∥AB.
【巩固练习】
一、选择题。
1、如图,若,则下列结论一定成立的是( )。
A. B.
C. D.
【答案】D;【解析】因为∠1=∠3,所以AD∥BC,所以∠1+∠2=180°,故选D.
2、如图,将三角板的直角顶点放在直尺的一边上,若,则的度数为( )。
A. B. C. D.
【答案】C
【解析】如图,因为AD∥BC,所以∠1=∠3=65°,因为∠2+∠3+90°=180°,所以∠2=90°-∠3=90°-65°=25°,故选C.
3、下列语句:①三角形的内角和是180°;②作一个角等于一个已知角;③两条直线被第三条直线所截,同位角相等;④延长线段AB到C,使BC=AB,其中是命题的有( )。
A.①② B.②③ C.①④ D.①③
【答案】D
【解析】①三角形的内角和是180°,是命题;②作一个角等于一个已知角,不是命题;③两条直线被第三条直线所截,同位角相等,是命题;④延长线段AB到C,使BC=AB,不是命题,故选D.
4、下列命题中,是真命题的是( )。
A.互补的角是邻补角 B.相等的角是对顶角
C.内错角相等 D.对顶角都相等
【答案】D
【解析】A、两直线平行时,同旁内角互补,此时这一对同旁内角不是邻补角,故本选项错误;
B、等腰三角形的两个底角相等,此时这两个底角不是对顶角,故本选项错误;
C、只有两直线平行时,内错角才相等,故本选项错误;?
D、对顶角都相等,故本选项正确.?
故选D.
5、如图,已知AB∥CD∥EF,则∠x、∠y、∠z三者之间的关系是( )。
A. B.
C. D.
【答案】B;【解析】∵∠y+∠CEF=180°,∠CEF=∠x—∠z,∴∠X+∠Y—∠Z=180°,故选B。
二、填空题。
6、如图,AB∥CD,直线l分别交AB、CD于E,F,∠1=56°,则∠2的度数是________°.
【答案】124
【解析】∵∠1=56°,∴∠3=180°?∠1=124°,∵AB∥CD,∴∠2=∠3=124°.
故答案为:124.
7、如图,a∥b,AC分别交直线a、b于点B、C,,若,则__________度.
【答案】65
【解析】∵AC⊥DC,∴∠1+∠3=90°,∵∠1=25°,∴∠3=90°-∠1=90°-25°=65°,
∵a∥b,∴∠2=∠1=65°,故答案为:65.
8、如图,AB∥CD,∠B=115°,∠C=45°,则∠BEC=__________.
【答案】110°
【解析】如图,过点E作EF∥AB.因为AB∥CD,所以EF∥CD,所以∠B+∠BEF=180°,∠C=∠CEF.
因为∠B=115°,∠C=45°,所以∠BEF=180°-115°=65°,∠CEF=45°,所以∠BEC=∠BEF+∠CEF=65°+45°=110°,故答案为:110°.
9、如图,一条公路修到湖边时,需拐弯绕湖而过,在A,B,C三处经过三次拐弯,此时道路恰好和第一次拐弯之前的道路平行(即AE∥CD),若∠A=120°,∠B=150°,则∠C的度数是__________.
【答案】150°
【解析】如图,过点B作BG∥AE,∵AE∥CD,∴AE∥BG∥CD。
∴∠A=∠2,∠1+∠C=180°,∵∠A=120°,∴∠2=120°,∴∠1=150°—120°=30°,
∴∠C=180°—30°=150°,故答案为:150°。
10、“直角都相等”的题设是两个角是直角,结论是这两个角相等.
三、证明题。
11、如图,∠1+∠2=180°,∠B=∠E,试猜想AB与CE之间有怎样的位置关系?并说明理由.
【解析】AB∥CE,理由如下:
∵∠1+∠2=180°,
∴DE∥BC(同旁内角互补,两直线平行),
∴∠ADF=∠B(两直线平行,同位角相等),
∵∠B=∠E,
∴∠ADF=∠E,∴AB∥CE(内错角相等,两直线平行).
12、如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
解:∵直线AB∥CD,∠1=65°,
∴∠ABC=∠1=65°.
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°.
∵直线AB∥CD,∴∠ABD+∠BDC=180°.
∴∠2=∠BDC=180°-∠ABD=180°-130°=50°.
13、如图,于,交于点,交于点,,,试判断和的位置关系,并说明理由.
【解析】如图,过点作.
∵,∴(两直线平行,同位角相等).
∵(已知),∴(等量代换).
∵(已知),∴(垂直的定义),
∴.
∵,∴,
∴(同旁内角互补,两直线平行),
∴(平行于同一条直线的两条直线互相平行).
14、如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°.
又∵DE∥CF,∠CDE=130°,
∴∠DCF+∠CDE=180°.∴∠DCF=50°.
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
15、阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
解:过点P作PE∥AB.
∵AB∥CD,∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
解:如图乙,过点P作PE∥AB.
∵AB∥CD(已知),
∴PE∥AB∥CD(平行于同一直线的两条直线平行).
∴∠A=∠EPA,∠EPC=∠C(两直线平行,内错角相等).
∵∠APC=∠EPA+∠EPC,
∴∠APC=∠A+∠C(等量代换).
如图丙,过点P作PF∥AB.
∴∠FPA=∠A(两直线平行,内错角相等).
∵AB∥CD(已知),∴PF∥CD(平行于同一直线的两条直线平行).
∴∠FPC=∠C(两直线平行,内错角相等).
∵∠FPC-∠FPA=∠APC,
∴∠C-∠A=∠APC(等量代换).
