第二章 四边形单元练习题(含解析)
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册第二章
四边形
单元练习
一、单选题(共10题;共40分)
1.从一个多边形的一个顶点出发可以引5条对角线,则这个多边形的内角和为(??
)
A.?900°??????????????????????????????????B.?1080°??????????????????????????????????C.?1260°??????????????????????????????????D.?1440°
2.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是(??
)
A.?OA=OC??????????????????????????B.?AB=CD??????????????????????????C.?AD=BC??????????????????????????D.?∠ABD=∠CBD
3.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是(??
)
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
4.以下关于新型冠状病毒
的防范宣传图标中是中心对称图形的是(?
)
A.???????????????B.???????????????C.???????????????D.?
5.如图,在四边形
中,点P是边
上的一个动点,点Q是边
上的一个定点,连接
和
,点E和F分别是
和
的中点,则随着点P的运动,线段
的长(??
)
A.?逐渐变大?????????????????????????B.?逐渐变小?????????????????????????C.?先变小再变大?????????????????????????D.?始终不变
6.如图,矩形
的两条对角线相交于点
,
,则线段
的长为(????
)
A.?8???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
7.如图,平行四边形ABCD的对角线AC与BD相交于点O
,
添加一个条件不能使平行四边形ABCD变为矩形的是(??
)
A.?OA=OC?????????????????????????B.?AC=BD?????????????????????????C.?DA⊥AB?????????????????????????D.?∠OAB=∠OBA
8.下面性质中,菱形不一定具备的是(??
)
A.?四条边都相等???????????????B.?每一条对角线平分一组对角???????????????C.?邻角互补???????????????D.?对角线相等
9.已知平行四边形
的对角线相交于点
,补充下列四个条件,能使平行四边形
成为菱形的是(???
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
10.直角梯形ABCD中,∠A=∠D=90°,DC<AB,AB=AD=12,E是边AD上的一点,恰好使CE=10,并且∠CBE=45°,则AE的长是( )
A.?2或8??????????????????????????????????????B.?4或6??????????????????????????????????????C.?5??????????????????????????????????????D.?3或7
二、填空题(共5题;共20分)
11.若一个多边形的每个外角都是40°,则从这个多边形的一个顶点出发可以画________条对角线.
12.如图,在
中,
,D是BC上的任一点,
交AC于点E,
交AB于点F那么四边形AFDE的周长是________.
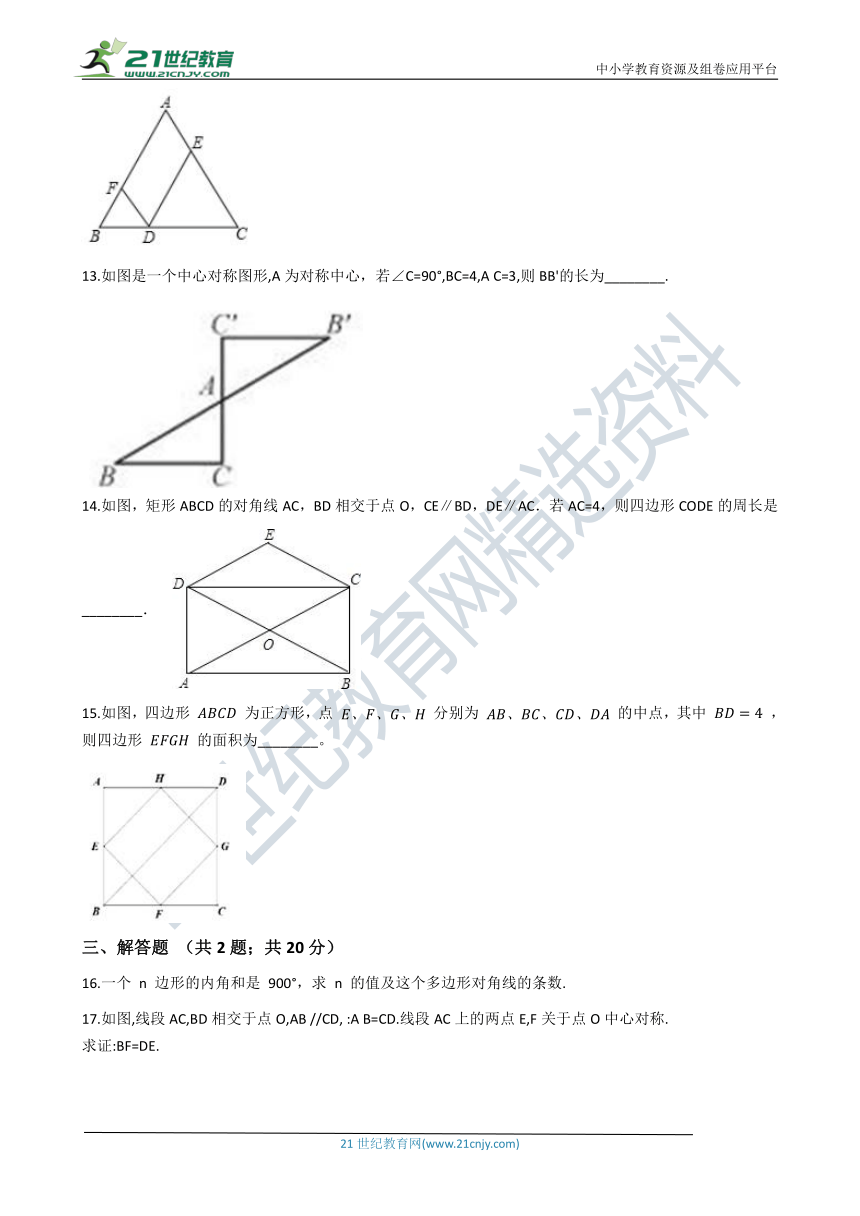
13.如图是一个中心对称图形,A为对称中心,若∠C=90°,BC=4,A
C=3,则BB'的长为________.
14.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是________.
15.如图,四边形
为正方形,点
分别为
的中点,其中
,则四边形
的面积为________。
解答题
(共2题;共20分)
16.一个
n
边形的内角和是
900°,求
n
的值及这个多边形对角线的条数.
17.如图,线段AC,BD相交于点O,AB
//CD,
:A
B=CD.线段AC上的两点E,F关于点O中心对称.
求证:BF=DE.
四、综合题(共2题;共20分)
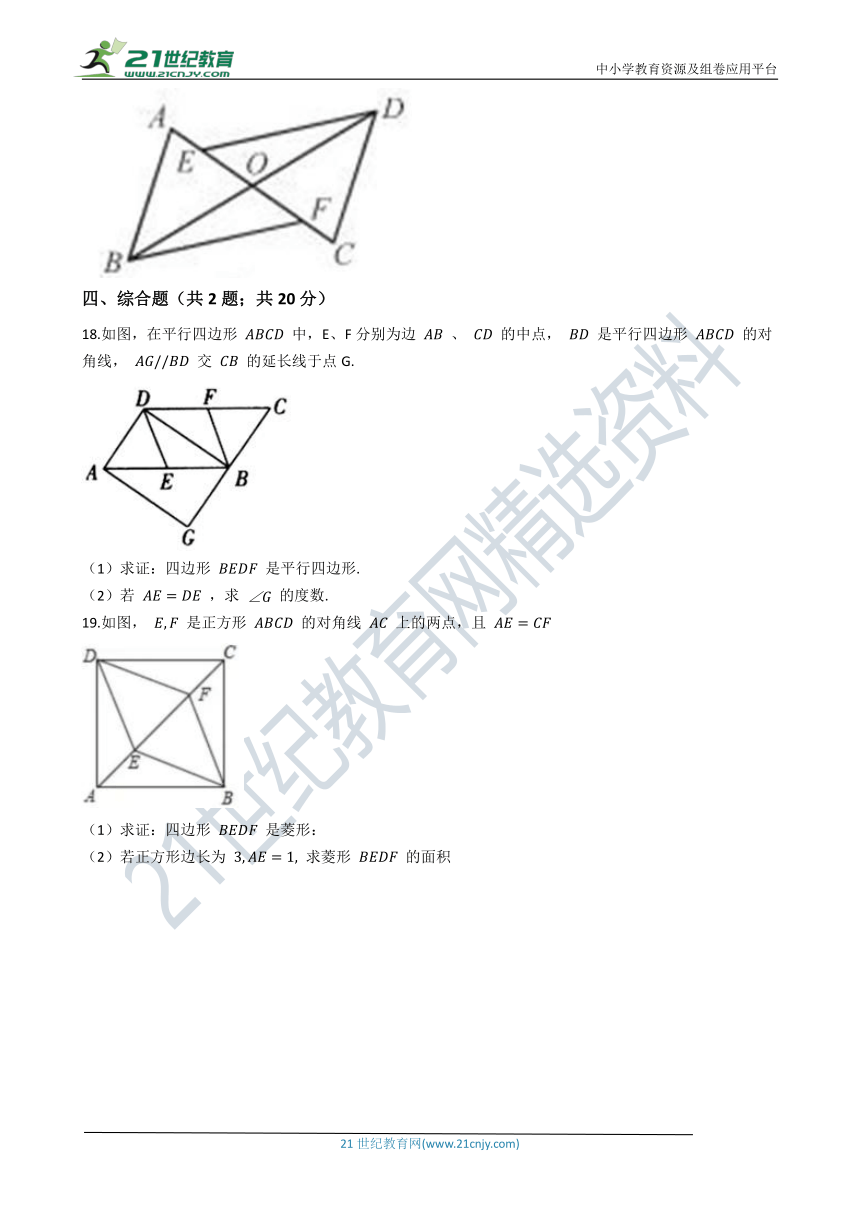
18.如图,在平行四边形
中,E、F分别为边
、
的中点,
是平行四边形
的对角线,
交
的延长线于点G.
(1)求证:四边形
是平行四边形.
(2)若
,求
的度数.
19.如图,
是正方形
的对角线
上的两点,且
(1)求证:四边形
是菱形:
(2)若正方形边长为
求菱形
的面积
答案解析部分
一、单选题
1.【答案】
B
解:设多边形边数为n,由题意得:
n﹣3=5,
n=8,
内角和:180°×(8﹣2)=1080°.
故答案为:B.
2.【答案】
D
解:A、∵平行四边形ABCD的对角线AC、BD相交于点O,
∴OA=OC,故此选项不符合题意;
B、∵四边形ABCD是平行四边形,
∴AB=CD,故此选项不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD=BC,故此选项不符合题意;
D、当四边形ABCD是菱形时,∠ABD=∠CBD,故此选项符合题意;
故答案为:D.
3.【答案】
C
解:∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故答案为:C.
4.【答案】
A
A.是中心对称图形,故此选项符合题意;
B.不是中心对称图形,故此选项不符合题意;
C.不是中心对称图形,故此选项不符合题意;
D.不是中心对称图形,故此选项不符合题意;
故答案为:A.
5.【答案】
D
解:连接AQ,如图,
∵点Q是边BC上的定点,
∴AQ的大小不变,
∵E,F分别是AP,PQ的中点,
∴EF=
AQ,
∴线段EF的长度保持不变,
故答案为:D.
6.【答案】
D
根据矩形的性质:矩形的对角线互相平分且相等,可知
,
故答案为:D.
7.【答案】
A
∵四边形ABCD为平行四边形,要是其成为一矩形,
B、AC=BD,所以平行四边形ABCD是矩形,不能满足条件,B不符合题意;
C、由
得
,所以平行四边形ABCD是矩形,不能满足条件,C不符合题意;
D、由
得OA=OB,则AC=BD,所以平行四边形ABCD是矩形,不能满足条件,D不符合题意.
故答案为:A.
8.【答案】
D
A.
菱形的四条边都相等,说法正确,不符合题意;
B.
菱形的每一条对角线平分一组对角,说法正确,不符合题意;
C.
菱形的邻角互补,说法正确,不符合题意;
D.
菱形的对角线不一定相等,说法不正确,符合题意.
故答案为:D.
9.【答案】
D
解:A、
,不能判断?ABCD是菱形,不符合题意;
B、
,对角线相等的平行四边形是矩形,不一定是菱形,不符合题意;
C、
,有一个角是直角的平行四边形是矩形,不一定是菱形,不符合题意;
D、
,根据菱形的判定:对角线互相垂直的平行四边形是菱形可得,?ABCD是菱形,符合题意;
故答案为:D.
10.【答案】
B
解:如图,过点B作BF⊥CD交DC的延长线于F,
∵∠A=∠D=90°,AB=AD,
∴四边形ABFD是正方形,
把△ABE绕点B顺时针旋转90°得到△BFG,
则AE=FG,BE=BG,∠ABE=∠FBG,
∵∠CBE=45°,
∴∠CBG=∠CBF+∠FBG=∠CBF+∠ABE=90°﹣∠CBE=90°﹣45°=45°,
∴∠CBE=∠CBG,
在△CBE和△CBG中,
∴△CBE≌△CBG(SAS),
∴CE=CG,
∴AE+CF=FG+CF=CG=CE,
设AE=x,则DE=12﹣x,CF=10﹣x,
∴CD=12﹣(10﹣x)=x+2,
在Rt△CDE中,CD2+DE2=CE2
,
即(x+2)2+(12﹣x)2=102
,
整理得,x2﹣10x+24=0,
解得x1=4,x2=6,
所以AE的长是4或6.
故选B.
二、填空题
11.【答案】
6
解:∵一个多边形的每个外角都是40°,
∴该多边形的边数为360°÷40°=9,
则从这个多边形的一个顶点出发可以画9﹣3=6条对角线.
故答案为6.
12.【答案】
16
解:∵DE∥AB,DF∥AC,
则四边形AFDE是平行四边形,
∠B=∠EDC,∠FDB=∠C
∵AB=AC,
∴∠B=∠C,
∴∠B=∠FDB,∠C=∠EDF
∴BF=FD,DE=EC,
所以:?AFDE的周长等于AB+AC=16.
故答案为:16.
13.【答案】
10
解:在△ABC中,
∠C=90°,BC=4,A
C=3
,
∴AB==5,
∵?此图一个中心对称图形,A为对称中心
,
∴△ABC≌△A'B'C',
∴AB=AB'=5,
∴BB'=10.
故答案为:10.
14.【答案】8
解:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴OC=
AC=2,OD=
BD,AC=BD,
∴OC=OD=2,
∴四边形CODE是菱形,
∴DE=CEOC=OD=2,
∴四边形CODE的周长=2×4=8;
故答案为:8.
15.【答案】
4
解:∵四边形ABCD是正方形,点E、F、G、H分别是AB、BC、CD、DA的中点,
∴△AEH、△BEF、△CFG、△DGH都为等腰直角三角形,
∴∠HEF、∠EFG、∠FGH、∠GHE都为直角,
∴四边形EFGH是矩形,
边接AC,则AC=BD=4,
又∵EH是△ABD的中位线,
∴EH=
BD=2,
同理EF=
AC=2,
∴四边形EFGH的面积为2×2=4.
故答案为:4.
三、解答题
16.
解:多边形的边数
;
对角线的条数:
.
故
,这个多边形的对角线共有14条.
17.
证明:∵AB∥CD,∴∠A=∠C,∵∠AOB=∠COD,AB=CD,∴△ABO≌△CDO(AAS)∴BO=DO,∵
E,F关于点O中心对称,∴OE=OF,∵∠BOF=∠DOE,∴△BOF≌△DOE(SAS),∴BF=DE.
四、综合题
18.(1)证明:∵四边形
是平行四边形,
分别为边
的中点,
,
.
∵BE∥DF,
∴四边形
是平行四边形.
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BG,
∵AG∥BD,
∴四边形AGBD是平行四边形,
∵点E是AB的中点,
∴AE=BE=
AB,
∵AE=DE,
∴AE=DE=BE,
∴∠DAE=∠ADE,∠EDB=∠EBD,
∵∠DAE+∠ADE+∠EDB+∠EBD=180°,
∴2∠ADE+2∠EDB=180°,
∴∠ADE+∠EDB=90°,即∠ADB=90°,
∴平行四边形AGBD是矩形.
∴∠G=90°.
(2)先证明四边形AGBD是平行四边形,再证出∠ADB=90°,得到四边形AGBD为矩形,即可得出结论.
19.(1)证明:∵四边形ABCD是正方形,
∴AD=BC,AD∥BC,
∴∠DAC=∠BCA,
∵AE=CF,
∴ΔADE≌ΔCBF,
∴DE=BF,
同理DF=BE,
∴四边形BEDF是平行四边形,
∵∠ACB=∠ACD,BC=DC,CF=CF,
∴△BCF≌△DCF,
∴DF=BF,
∴平行四边形BEDF是菱形.
(2)解:连接BD,
∵正方形ABCD的边长为3,
∴AC=BD,∠ABC=90°,AB=AD=3,
∴Rt△ABC中,
AC=
,
∵AE=CF=1,
∴EF=
,
∴S菱形BEDF=
BD·EF=
.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册第二章
四边形
单元练习
一、单选题(共10题;共40分)
1.从一个多边形的一个顶点出发可以引5条对角线,则这个多边形的内角和为(??
)
A.?900°??????????????????????????????????B.?1080°??????????????????????????????????C.?1260°??????????????????????????????????D.?1440°
2.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误的是(??
)
A.?OA=OC??????????????????????????B.?AB=CD??????????????????????????C.?AD=BC??????????????????????????D.?∠ABD=∠CBD
3.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是(??
)
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?②④
4.以下关于新型冠状病毒
的防范宣传图标中是中心对称图形的是(?
)
A.???????????????B.???????????????C.???????????????D.?
5.如图,在四边形
中,点P是边
上的一个动点,点Q是边
上的一个定点,连接
和
,点E和F分别是
和
的中点,则随着点P的运动,线段
的长(??
)
A.?逐渐变大?????????????????????????B.?逐渐变小?????????????????????????C.?先变小再变大?????????????????????????D.?始终不变
6.如图,矩形
的两条对角线相交于点
,
,则线段
的长为(????
)
A.?8???????????????????????????????????????????B.?4???????????????????????????????????????????C.?3???????????????????????????????????????????D.?2
7.如图,平行四边形ABCD的对角线AC与BD相交于点O
,
添加一个条件不能使平行四边形ABCD变为矩形的是(??
)
A.?OA=OC?????????????????????????B.?AC=BD?????????????????????????C.?DA⊥AB?????????????????????????D.?∠OAB=∠OBA
8.下面性质中,菱形不一定具备的是(??
)
A.?四条边都相等???????????????B.?每一条对角线平分一组对角???????????????C.?邻角互补???????????????D.?对角线相等
9.已知平行四边形
的对角线相交于点
,补充下列四个条件,能使平行四边形
成为菱形的是(???
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
10.直角梯形ABCD中,∠A=∠D=90°,DC<AB,AB=AD=12,E是边AD上的一点,恰好使CE=10,并且∠CBE=45°,则AE的长是( )
A.?2或8??????????????????????????????????????B.?4或6??????????????????????????????????????C.?5??????????????????????????????????????D.?3或7
二、填空题(共5题;共20分)
11.若一个多边形的每个外角都是40°,则从这个多边形的一个顶点出发可以画________条对角线.
12.如图,在
中,
,D是BC上的任一点,
交AC于点E,
交AB于点F那么四边形AFDE的周长是________.
13.如图是一个中心对称图形,A为对称中心,若∠C=90°,BC=4,A
C=3,则BB'的长为________.
14.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是________.
15.如图,四边形
为正方形,点
分别为
的中点,其中
,则四边形
的面积为________。
解答题
(共2题;共20分)
16.一个
n
边形的内角和是
900°,求
n
的值及这个多边形对角线的条数.
17.如图,线段AC,BD相交于点O,AB
//CD,
:A
B=CD.线段AC上的两点E,F关于点O中心对称.
求证:BF=DE.
四、综合题(共2题;共20分)
18.如图,在平行四边形
中,E、F分别为边
、
的中点,
是平行四边形
的对角线,
交
的延长线于点G.
(1)求证:四边形
是平行四边形.
(2)若
,求
的度数.
19.如图,
是正方形
的对角线
上的两点,且
(1)求证:四边形
是菱形:
(2)若正方形边长为
求菱形
的面积
答案解析部分
一、单选题
1.【答案】
B
解:设多边形边数为n,由题意得:
n﹣3=5,
n=8,
内角和:180°×(8﹣2)=1080°.
故答案为:B.
2.【答案】
D
解:A、∵平行四边形ABCD的对角线AC、BD相交于点O,
∴OA=OC,故此选项不符合题意;
B、∵四边形ABCD是平行四边形,
∴AB=CD,故此选项不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD=BC,故此选项不符合题意;
D、当四边形ABCD是菱形时,∠ABD=∠CBD,故此选项符合题意;
故答案为:D.
3.【答案】
C
解:∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故答案为:C.
4.【答案】
A
A.是中心对称图形,故此选项符合题意;
B.不是中心对称图形,故此选项不符合题意;
C.不是中心对称图形,故此选项不符合题意;
D.不是中心对称图形,故此选项不符合题意;
故答案为:A.
5.【答案】
D
解:连接AQ,如图,
∵点Q是边BC上的定点,
∴AQ的大小不变,
∵E,F分别是AP,PQ的中点,
∴EF=
AQ,
∴线段EF的长度保持不变,
故答案为:D.
6.【答案】
D
根据矩形的性质:矩形的对角线互相平分且相等,可知
,
故答案为:D.
7.【答案】
A
∵四边形ABCD为平行四边形,要是其成为一矩形,
B、AC=BD,所以平行四边形ABCD是矩形,不能满足条件,B不符合题意;
C、由
得
,所以平行四边形ABCD是矩形,不能满足条件,C不符合题意;
D、由
得OA=OB,则AC=BD,所以平行四边形ABCD是矩形,不能满足条件,D不符合题意.
故答案为:A.
8.【答案】
D
A.
菱形的四条边都相等,说法正确,不符合题意;
B.
菱形的每一条对角线平分一组对角,说法正确,不符合题意;
C.
菱形的邻角互补,说法正确,不符合题意;
D.
菱形的对角线不一定相等,说法不正确,符合题意.
故答案为:D.
9.【答案】
D
解:A、
,不能判断?ABCD是菱形,不符合题意;
B、
,对角线相等的平行四边形是矩形,不一定是菱形,不符合题意;
C、
,有一个角是直角的平行四边形是矩形,不一定是菱形,不符合题意;
D、
,根据菱形的判定:对角线互相垂直的平行四边形是菱形可得,?ABCD是菱形,符合题意;
故答案为:D.
10.【答案】
B
解:如图,过点B作BF⊥CD交DC的延长线于F,
∵∠A=∠D=90°,AB=AD,
∴四边形ABFD是正方形,
把△ABE绕点B顺时针旋转90°得到△BFG,
则AE=FG,BE=BG,∠ABE=∠FBG,
∵∠CBE=45°,
∴∠CBG=∠CBF+∠FBG=∠CBF+∠ABE=90°﹣∠CBE=90°﹣45°=45°,
∴∠CBE=∠CBG,
在△CBE和△CBG中,
∴△CBE≌△CBG(SAS),
∴CE=CG,
∴AE+CF=FG+CF=CG=CE,
设AE=x,则DE=12﹣x,CF=10﹣x,
∴CD=12﹣(10﹣x)=x+2,
在Rt△CDE中,CD2+DE2=CE2
,
即(x+2)2+(12﹣x)2=102
,
整理得,x2﹣10x+24=0,
解得x1=4,x2=6,
所以AE的长是4或6.
故选B.
二、填空题
11.【答案】
6
解:∵一个多边形的每个外角都是40°,
∴该多边形的边数为360°÷40°=9,
则从这个多边形的一个顶点出发可以画9﹣3=6条对角线.
故答案为6.
12.【答案】
16
解:∵DE∥AB,DF∥AC,
则四边形AFDE是平行四边形,
∠B=∠EDC,∠FDB=∠C
∵AB=AC,
∴∠B=∠C,
∴∠B=∠FDB,∠C=∠EDF
∴BF=FD,DE=EC,
所以:?AFDE的周长等于AB+AC=16.
故答案为:16.
13.【答案】
10
解:在△ABC中,
∠C=90°,BC=4,A
C=3
,
∴AB==5,
∵?此图一个中心对称图形,A为对称中心
,
∴△ABC≌△A'B'C',
∴AB=AB'=5,
∴BB'=10.
故答案为:10.
14.【答案】8
解:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴OC=
AC=2,OD=
BD,AC=BD,
∴OC=OD=2,
∴四边形CODE是菱形,
∴DE=CEOC=OD=2,
∴四边形CODE的周长=2×4=8;
故答案为:8.
15.【答案】
4
解:∵四边形ABCD是正方形,点E、F、G、H分别是AB、BC、CD、DA的中点,
∴△AEH、△BEF、△CFG、△DGH都为等腰直角三角形,
∴∠HEF、∠EFG、∠FGH、∠GHE都为直角,
∴四边形EFGH是矩形,
边接AC,则AC=BD=4,
又∵EH是△ABD的中位线,
∴EH=
BD=2,
同理EF=
AC=2,
∴四边形EFGH的面积为2×2=4.
故答案为:4.
三、解答题
16.
解:多边形的边数
;
对角线的条数:
.
故
,这个多边形的对角线共有14条.
17.
证明:∵AB∥CD,∴∠A=∠C,∵∠AOB=∠COD,AB=CD,∴△ABO≌△CDO(AAS)∴BO=DO,∵
E,F关于点O中心对称,∴OE=OF,∵∠BOF=∠DOE,∴△BOF≌△DOE(SAS),∴BF=DE.
四、综合题
18.(1)证明:∵四边形
是平行四边形,
分别为边
的中点,
,
.
∵BE∥DF,
∴四边形
是平行四边形.
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BG,
∵AG∥BD,
∴四边形AGBD是平行四边形,
∵点E是AB的中点,
∴AE=BE=
AB,
∵AE=DE,
∴AE=DE=BE,
∴∠DAE=∠ADE,∠EDB=∠EBD,
∵∠DAE+∠ADE+∠EDB+∠EBD=180°,
∴2∠ADE+2∠EDB=180°,
∴∠ADE+∠EDB=90°,即∠ADB=90°,
∴平行四边形AGBD是矩形.
∴∠G=90°.
(2)先证明四边形AGBD是平行四边形,再证出∠ADB=90°,得到四边形AGBD为矩形,即可得出结论.
19.(1)证明:∵四边形ABCD是正方形,
∴AD=BC,AD∥BC,
∴∠DAC=∠BCA,
∵AE=CF,
∴ΔADE≌ΔCBF,
∴DE=BF,
同理DF=BE,
∴四边形BEDF是平行四边形,
∵∠ACB=∠ACD,BC=DC,CF=CF,
∴△BCF≌△DCF,
∴DF=BF,
∴平行四边形BEDF是菱形.
(2)解:连接BD,
∵正方形ABCD的边长为3,
∴AC=BD,∠ABC=90°,AB=AD=3,
∴Rt△ABC中,
AC=
,
∵AE=CF=1,
∴EF=
,
∴S菱形BEDF=
BD·EF=
.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
