2.6.2 菱形的判定同步练习(含解析)
文档属性
| 名称 | 2.6.2 菱形的判定同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册2.6.2菱形的判定 同步练习
一、单选题
1.在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( )
A. BC=CD B. AB=CD C. ∠D=90° D. AD=BC
2.下列条件中,不能判定四边形ABCD为菱形的是( ).
A. AC⊥BD,AC与BD互相平分 B. AB=BC=CD=DA
C. AB=BC,AD=CD,且AC⊥BD D. AB=CD,AD=BC,AC⊥BD
3.如图,某同学作线段AB的垂直平分线:分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于点C,D,则直线CD为线段AB的垂直平分线.根据这个同学的作图方法可知四边形ADBC一定是( )
A. 菱形 B. 平行四边形 C. 矩形 D. 一般的四边形
4.如图,若要使平行四边形ABCD成为菱形,需添加的条件是( )
A. B. C. D. 互相垂直
5.如图,在一张平行四边形纸片ABCD中,画一个菱形,甲、乙两位同学的画法如下:
甲:以B , A为圆心,AB长为半径作弧,分别交BC , AD于点E , F,则四边形ABEF为菱形;乙:作∠A, ∠B的平分线AE , BF , 分别交BC于点E , 交AD于点F , 则四边形ABEF是菱形;关于甲、乙两人的画法,下列判断正确的是( )
A. 仅甲正确 B. 仅乙正确 C. 甲、乙均正确 D. 甲、乙均错误
6.如图, 中, 平分 , 交 于 , 交 于 ,若 ,则四边形 的周长是( )
A. 24 B. 28 C. 32 D. 36
7.有两张宽为3,长为9的矩形纸片如图所示叠放在一起,使重叠的部分构成一个四边形,则四边形的最大面积是( )
A. 27 B. 12 C. 15 D. 18
8.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
A. 16 B. 15 C. 14 D. 13
9.如图,是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:对于甲、乙两人的作法,可判断( )
A. 甲、乙均正确 B. 甲、乙均错误 C. 甲正确,乙错误 D. 甲错误,乙正确
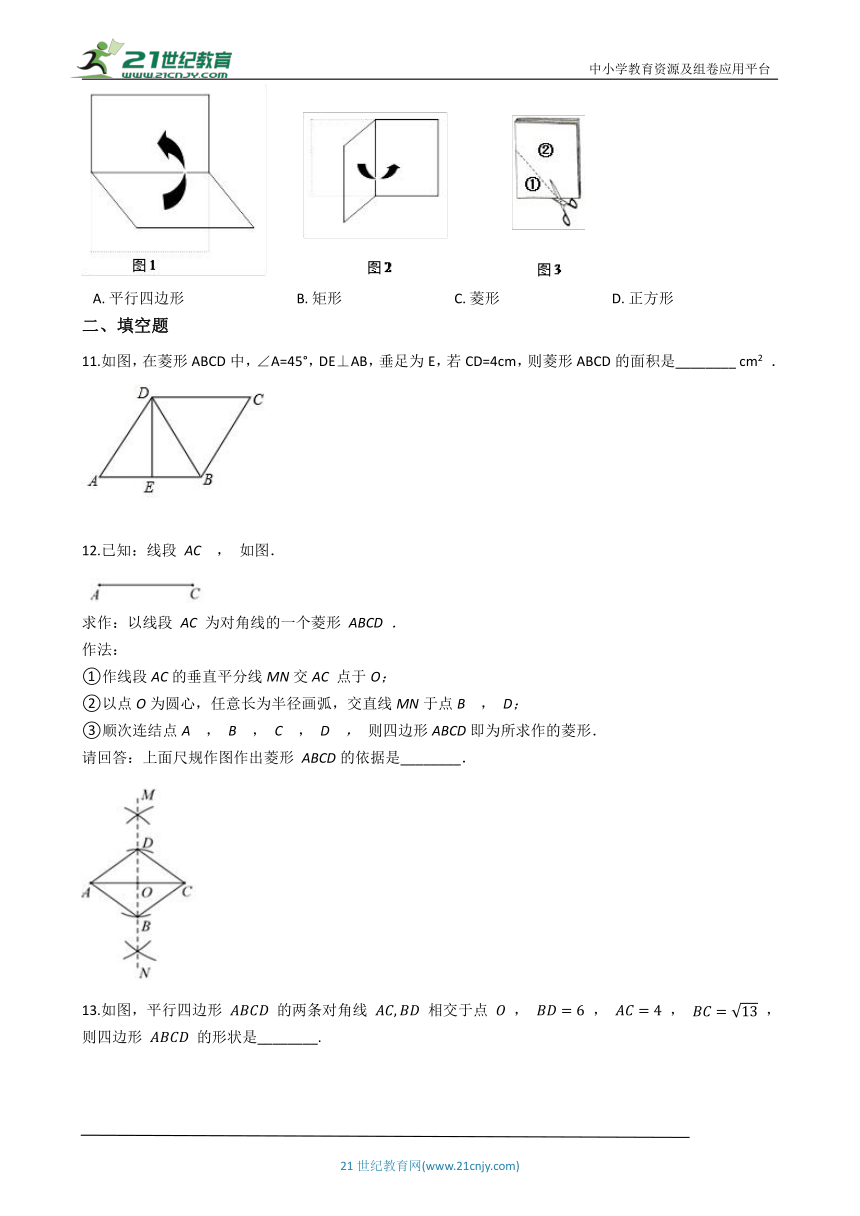
10.将一矩形纸片对折后再对折,如图1、图2,然后沿图3中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形一定是( ).
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
二、填空题
11.如图,在菱形ABCD中,∠A=45°,DE⊥AB,垂足为E,若CD=4cm,则菱形ABCD的面积是________ cm2 .
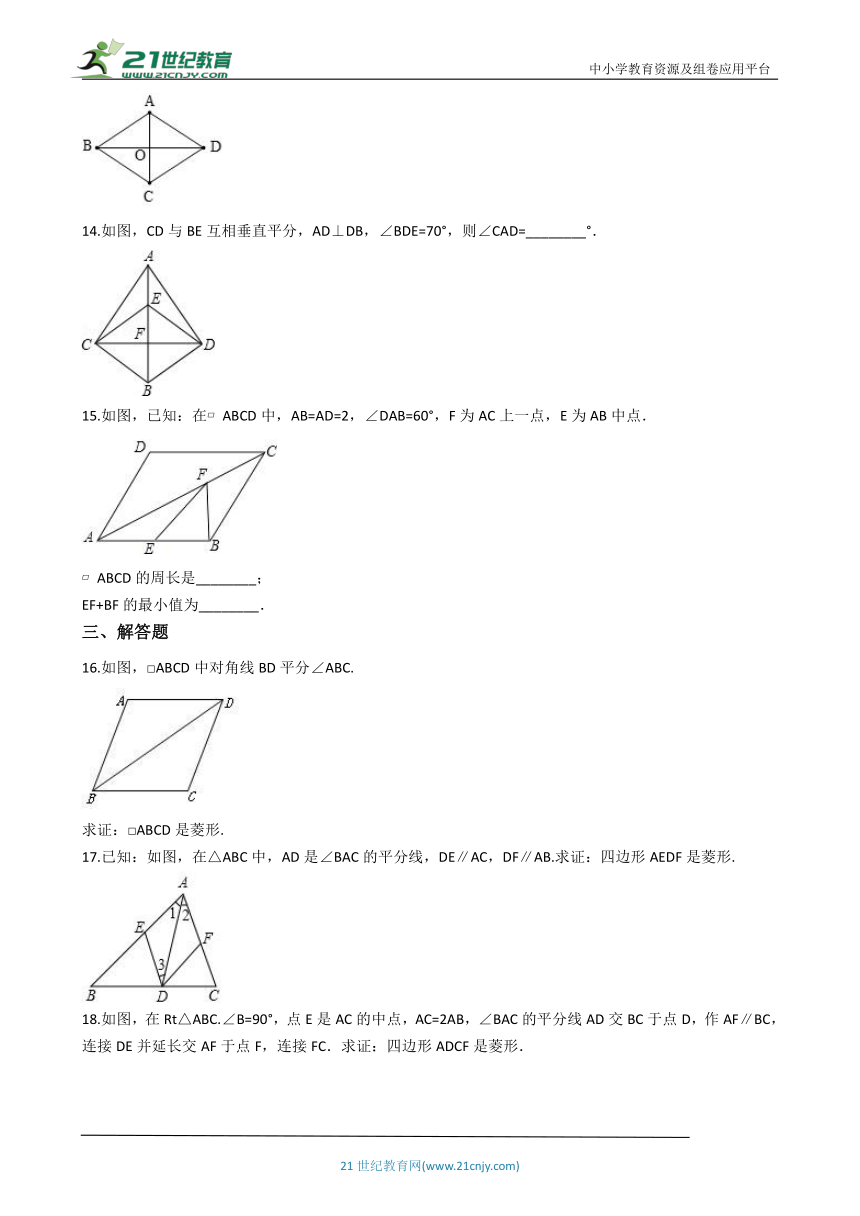
12.已知:线段 AC , 如图.
求作:以线段 AC 为对角线的一个菱形 ABCD .
作法:
①作线段AC的垂直平分线MN交AC 点于O;
②以点O为圆心,任意长为半径画弧,交直线MN于点B , D;
③顺次连结点A , B , C , D , 则四边形ABCD即为所求作的菱形.
请回答:上面尺规作图作出菱形 ABCD的依据是________.
13.如图,平行四边形 的两条对角线 相交于点 , , , ,则四边形 的形状是________.
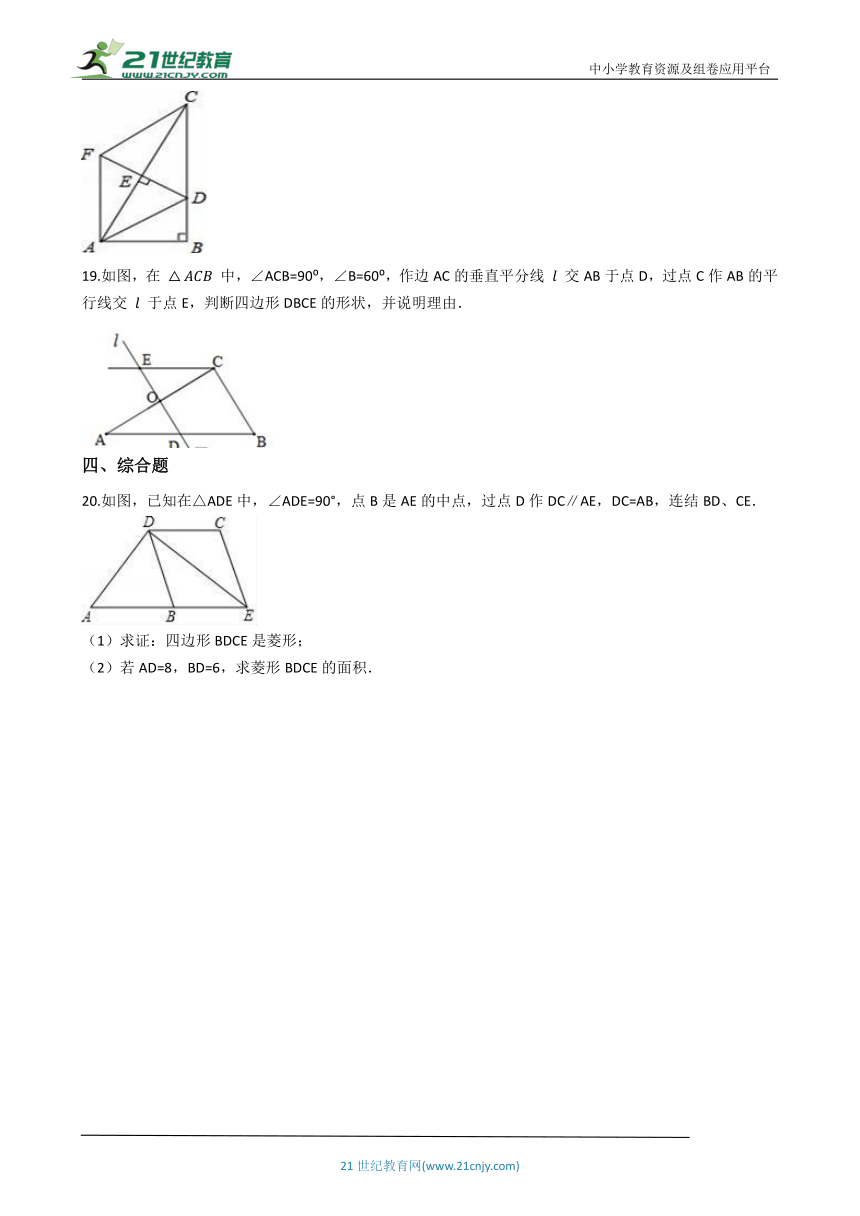
14.如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=________°.
15.如图,已知:在 ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.
ABCD的周长是________;
EF+BF的最小值为________.
三、解答题
16.如图,□ABCD中对角线BD平分∠ABC.
求证:□ABCD是菱形.
17.已知:如图,在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.
18.如图,在Rt△ABC.∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.
19.如图,在 中,∠ACB=90 ,∠B=60 ,作边AC的垂直平分线 交AB于点D,过点C作AB的平行线交 于点E,判断四边形DBCE的形状,并说明理由.
四、综合题
20.如图,已知在△ADE中,∠ADE=90°,点B是AE的中点,过点D作DC∥AE,DC=AB,连结BD、CE.
(1)求证:四边形BDCE是菱形;
(2)若AD=8,BD=6,求菱形BDCE的面积.
答案解析部分
一、单选题
1.【答案】 A
解:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
如下图,
若BC=CD,则平行四边形ABCD是菱形;
若AB=CD,则还是平行四边形;
若∠ADC=90°,则平行四边形ABCD是矩形;
若AD=BC,则还是平行四边形;
故答案为:A.
2.【答案】 C
解:A、根据AC与BD互相平分得四边形ABCD是平行四边形,再有AC⊥BD ,可得此四边形是菱形;
B、根据AB=BC=CD=DA ,可知四边形是菱形;
C、由AB=BC,AD=CD,不能得到此四边形是平行四边形,所以不能判定四边形ABCD是菱形;
D、由AB=CD,AD=BC得四边形是平行四边形,再有AC⊥BD,可得四边形是菱形.
故答案为:C.
3.【答案】 A
解:∵分别以A和B为圆心,大于 AB的长为半径画弧,两弧相交于C、D,
∴AC=AD=BD=BC,
∴四边形ADBC一定是菱形,
故答案为:A.
4.【答案】 D
解:由平行四边形的性质可得: , ,则选项A不符题意
,则选项B不符题意
若 ,则
对角线相等的平行四边形一定是矩形,但不一定是菱形,则选项C不符题意
对角线互相垂直的平行四边形是菱形,则选项D符合题意
故答案为:D.
5.【答案】 C
解:甲的作法正确;
证明:由题意得AB=AF,AB=BE,
∴AF=BE,
又∵AF∥BE,∴四边形ABEF是平行四边形,
又∵AB=BE,∴四边形ABEF是平行菱形。
乙的作法正确;
证明:∵AD∥BC ,
∴∠1=∠2 , ∠6=∠7 ,
∵BF平分∠ABC , AE平分∠BAD ,
∴∠2=∠3 , ∠5=∠6 ,
∴∠1=∠3 , ∠5=∠7 ,
∴AB=AF , AB=BE ,
∴AF=BE
∵AF∥BE , 且AF=BE ,
∴四边形ABEF是平行四边形,
∵AB=AF ,
∴平行四边形ABEF是菱形。
故答案为:C
6.【答案】 A
解:∵DE // AC, DF // AB,
∴四边形AEDF是平行四边形,∠BAD=∠ADF,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠CAD=∠ADF,
∴DF=AF=6,
∴平行四边形AEDF是菱形,
∴菱形AEDF的周长为:6×4=24,
故答案为:A.
7.【答案】 C
解:重叠的四边形的两组对边分别平行,那么可得是平行四边形,再根据宽度相等,利用面积的不同求法可得一组邻边相等,那么重叠的四边形应为菱形;如图,
此时菱形ABCD的面积最大.
设AB=x,EB=9-x,AE=3,
则由勾股定理得到:32+(9-x)2=x2 ,
解得x=5,
S最大=5×3=15.
故答案为:C.
8.【答案】 A
解:连结EF,AE与BF交于点O,如图,
∵AO平分∠BAD,
∴∠1=∠2,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
同理:AF=BE,
又∵AF∥BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形,
∴AE⊥BF,OB=OF=6,OA=OE,
在Rt△AOB中,由勾股定理得:OA= = =8,
∴AE=2OA=16.
故选:A.
9.【答案】 A
解:根据菱形的判定定理及性质可得甲、乙的做好均正确.
10.【答案】 C
由折叠过程可得,该四边形的对角线互相垂直平分,
所以将①展开后得到的平面图形是菱形.
故答案为:C.
二、填空题
11.【答案】 8
解:∵四边形ABCD是菱形,
∴AB=AD=CD=4cm,
∵∠A=45°,DE⊥AB,
∴DE=AD sin45°=4×=2(cm),
∴S菱形ABCD=AB DE=8(cm2).
故答案为:8 .
12.【答案】 对角线垂直的平行四边形是菱形
解:∵由作法可知.OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.
故答案为:对角线垂直的平行四边形是菱形.
13.【答案】 菱形
【解析】【解答】∵四边形 是平行四边形;
∴,CO=OC=2,BO=OD=3;
∵ ,则CO2+ BO2=BC2;
∴∠ BOC=90°,则四边形ABCD为菱形.
14.【答案】 70.
解:∵CD与BE互相垂直平分,∴四边形BDEC是菱形.∴DB=DE.
∵∠BDE=70°,∴∠ABD= =55°.
∵AD⊥DB,∴∠BAD=90°﹣55°=35°.
根据轴对称性,四边形ACBD关于直线AB成轴对称,
∴∠BAC=∠BAD=35°.∴∠CAD=∠BAC+∠BAD=35°+35°=70°.
15.【答案】 8;
解:根据平行四边形有一组邻边相等得到四边形ABCD为菱形,然后计算四边形的周长;根据菱形的性质可知点B与点D关于AC对称,从而可知BF=DF,则EF+BF=EF+DF,当点D、F、B共线时,EF+BF有最小值,然后根据等边三角形的性质以及直角三角形的勾股定理得出最小值.
三、解答题
16.【答案】 证明:如图,
∵四边形ABCD是平行四边形
∴AD∥BC,
∴∠2=∠3.
又∵BD平分∠ABC,
∴∠1=∠2,
∴∠1=∠3,
∴ AB =AD,
∴□ABCD是菱形.
17.【答案】 解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵AD平分∠BAC,
∴∠1=∠2(角平分线的定义),
∵DE∥AC,
∴∠2=∠3(两直线平行,内错角相等),
∴∠1=∠3(等量代换),
∴AE=DE,
∴平行四边形AEDF是菱形.
18.【答案】 解:∵AF∥CD, ∴∠AFE=∠CDE,
在△AFE和△CDE. ,
∴△AEF≌△CED, ∴AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形,
∵∠B=90°,∠ACB=30°, ∴∠CAB=60°,
∵AD平分∠CAB, ∴∠DAC=∠DAB=30°=∠ACD,
∴DA=DC, ∴四边形ADCF是菱形.
19.【答案】 解:四边形DBCE是菱形,理由如下:
DE垂直平分AC,
,
,即 ,
,
,
四边形DBCE是平行四边形,
, ,
是 的中位线,
点D是AB的中点,
,
又 在 中, ,
,
,
平行四边形DBCE是菱形.
四、综合题
20.【答案】 (1)证明:在Rt△ADB中,∵∠ADB=90°,AB=BE,
∴DB= AB=AB=BE,
∵DC∥BE,DC=AB=BE,
∴四边形BECD是平行四边形,
∵BD=BE,
∴四边形BECD是菱形.
(2)解:连接BC交DE于O.
∵四边形DBEC是菱形,
∴BC⊥DE,
∴BO∥AD,∵AB=BE,
∴DO=OE,
∴OB= AD=4,OD==2 ,
∴BC=8,DE=4 ,
∴S菱形BDCE= BC DE=16 .
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册2.6.2菱形的判定 同步练习
一、单选题
1.在四边形ABCD中,AB∥CD,AD∥BC,如果再添加一个条件,即可推出该四边形是菱形,这个条件可以是( )
A. BC=CD B. AB=CD C. ∠D=90° D. AD=BC
2.下列条件中,不能判定四边形ABCD为菱形的是( ).
A. AC⊥BD,AC与BD互相平分 B. AB=BC=CD=DA
C. AB=BC,AD=CD,且AC⊥BD D. AB=CD,AD=BC,AC⊥BD
3.如图,某同学作线段AB的垂直平分线:分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于点C,D,则直线CD为线段AB的垂直平分线.根据这个同学的作图方法可知四边形ADBC一定是( )
A. 菱形 B. 平行四边形 C. 矩形 D. 一般的四边形
4.如图,若要使平行四边形ABCD成为菱形,需添加的条件是( )
A. B. C. D. 互相垂直
5.如图,在一张平行四边形纸片ABCD中,画一个菱形,甲、乙两位同学的画法如下:
甲:以B , A为圆心,AB长为半径作弧,分别交BC , AD于点E , F,则四边形ABEF为菱形;乙:作∠A, ∠B的平分线AE , BF , 分别交BC于点E , 交AD于点F , 则四边形ABEF是菱形;关于甲、乙两人的画法,下列判断正确的是( )
A. 仅甲正确 B. 仅乙正确 C. 甲、乙均正确 D. 甲、乙均错误
6.如图, 中, 平分 , 交 于 , 交 于 ,若 ,则四边形 的周长是( )
A. 24 B. 28 C. 32 D. 36
7.有两张宽为3,长为9的矩形纸片如图所示叠放在一起,使重叠的部分构成一个四边形,则四边形的最大面积是( )
A. 27 B. 12 C. 15 D. 18
8.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
A. 16 B. 15 C. 14 D. 13
9.如图,是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:对于甲、乙两人的作法,可判断( )
A. 甲、乙均正确 B. 甲、乙均错误 C. 甲正确,乙错误 D. 甲错误,乙正确
10.将一矩形纸片对折后再对折,如图1、图2,然后沿图3中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形一定是( ).
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
二、填空题
11.如图,在菱形ABCD中,∠A=45°,DE⊥AB,垂足为E,若CD=4cm,则菱形ABCD的面积是________ cm2 .
12.已知:线段 AC , 如图.
求作:以线段 AC 为对角线的一个菱形 ABCD .
作法:
①作线段AC的垂直平分线MN交AC 点于O;
②以点O为圆心,任意长为半径画弧,交直线MN于点B , D;
③顺次连结点A , B , C , D , 则四边形ABCD即为所求作的菱形.
请回答:上面尺规作图作出菱形 ABCD的依据是________.
13.如图,平行四边形 的两条对角线 相交于点 , , , ,则四边形 的形状是________.
14.如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=________°.
15.如图,已知:在 ABCD中,AB=AD=2,∠DAB=60°,F为AC上一点,E为AB中点.
ABCD的周长是________;
EF+BF的最小值为________.
三、解答题
16.如图,□ABCD中对角线BD平分∠ABC.
求证:□ABCD是菱形.
17.已知:如图,在△ABC中,AD是∠BAC的平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形.
18.如图,在Rt△ABC.∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.
19.如图,在 中,∠ACB=90 ,∠B=60 ,作边AC的垂直平分线 交AB于点D,过点C作AB的平行线交 于点E,判断四边形DBCE的形状,并说明理由.
四、综合题
20.如图,已知在△ADE中,∠ADE=90°,点B是AE的中点,过点D作DC∥AE,DC=AB,连结BD、CE.
(1)求证:四边形BDCE是菱形;
(2)若AD=8,BD=6,求菱形BDCE的面积.
答案解析部分
一、单选题
1.【答案】 A
解:∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
如下图,
若BC=CD,则平行四边形ABCD是菱形;
若AB=CD,则还是平行四边形;
若∠ADC=90°,则平行四边形ABCD是矩形;
若AD=BC,则还是平行四边形;
故答案为:A.
2.【答案】 C
解:A、根据AC与BD互相平分得四边形ABCD是平行四边形,再有AC⊥BD ,可得此四边形是菱形;
B、根据AB=BC=CD=DA ,可知四边形是菱形;
C、由AB=BC,AD=CD,不能得到此四边形是平行四边形,所以不能判定四边形ABCD是菱形;
D、由AB=CD,AD=BC得四边形是平行四边形,再有AC⊥BD,可得四边形是菱形.
故答案为:C.
3.【答案】 A
解:∵分别以A和B为圆心,大于 AB的长为半径画弧,两弧相交于C、D,
∴AC=AD=BD=BC,
∴四边形ADBC一定是菱形,
故答案为:A.
4.【答案】 D
解:由平行四边形的性质可得: , ,则选项A不符题意
,则选项B不符题意
若 ,则
对角线相等的平行四边形一定是矩形,但不一定是菱形,则选项C不符题意
对角线互相垂直的平行四边形是菱形,则选项D符合题意
故答案为:D.
5.【答案】 C
解:甲的作法正确;
证明:由题意得AB=AF,AB=BE,
∴AF=BE,
又∵AF∥BE,∴四边形ABEF是平行四边形,
又∵AB=BE,∴四边形ABEF是平行菱形。
乙的作法正确;
证明:∵AD∥BC ,
∴∠1=∠2 , ∠6=∠7 ,
∵BF平分∠ABC , AE平分∠BAD ,
∴∠2=∠3 , ∠5=∠6 ,
∴∠1=∠3 , ∠5=∠7 ,
∴AB=AF , AB=BE ,
∴AF=BE
∵AF∥BE , 且AF=BE ,
∴四边形ABEF是平行四边形,
∵AB=AF ,
∴平行四边形ABEF是菱形。
故答案为:C
6.【答案】 A
解:∵DE // AC, DF // AB,
∴四边形AEDF是平行四边形,∠BAD=∠ADF,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠CAD=∠ADF,
∴DF=AF=6,
∴平行四边形AEDF是菱形,
∴菱形AEDF的周长为:6×4=24,
故答案为:A.
7.【答案】 C
解:重叠的四边形的两组对边分别平行,那么可得是平行四边形,再根据宽度相等,利用面积的不同求法可得一组邻边相等,那么重叠的四边形应为菱形;如图,
此时菱形ABCD的面积最大.
设AB=x,EB=9-x,AE=3,
则由勾股定理得到:32+(9-x)2=x2 ,
解得x=5,
S最大=5×3=15.
故答案为:C.
8.【答案】 A
解:连结EF,AE与BF交于点O,如图,
∵AO平分∠BAD,
∴∠1=∠2,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
同理:AF=BE,
又∵AF∥BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形,
∴AE⊥BF,OB=OF=6,OA=OE,
在Rt△AOB中,由勾股定理得:OA= = =8,
∴AE=2OA=16.
故选:A.
9.【答案】 A
解:根据菱形的判定定理及性质可得甲、乙的做好均正确.
10.【答案】 C
由折叠过程可得,该四边形的对角线互相垂直平分,
所以将①展开后得到的平面图形是菱形.
故答案为:C.
二、填空题
11.【答案】 8
解:∵四边形ABCD是菱形,
∴AB=AD=CD=4cm,
∵∠A=45°,DE⊥AB,
∴DE=AD sin45°=4×=2(cm),
∴S菱形ABCD=AB DE=8(cm2).
故答案为:8 .
12.【答案】 对角线垂直的平行四边形是菱形
解:∵由作法可知.OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.
故答案为:对角线垂直的平行四边形是菱形.
13.【答案】 菱形
【解析】【解答】∵四边形 是平行四边形;
∴,CO=OC=2,BO=OD=3;
∵ ,则CO2+ BO2=BC2;
∴∠ BOC=90°,则四边形ABCD为菱形.
14.【答案】 70.
解:∵CD与BE互相垂直平分,∴四边形BDEC是菱形.∴DB=DE.
∵∠BDE=70°,∴∠ABD= =55°.
∵AD⊥DB,∴∠BAD=90°﹣55°=35°.
根据轴对称性,四边形ACBD关于直线AB成轴对称,
∴∠BAC=∠BAD=35°.∴∠CAD=∠BAC+∠BAD=35°+35°=70°.
15.【答案】 8;
解:根据平行四边形有一组邻边相等得到四边形ABCD为菱形,然后计算四边形的周长;根据菱形的性质可知点B与点D关于AC对称,从而可知BF=DF,则EF+BF=EF+DF,当点D、F、B共线时,EF+BF有最小值,然后根据等边三角形的性质以及直角三角形的勾股定理得出最小值.
三、解答题
16.【答案】 证明:如图,
∵四边形ABCD是平行四边形
∴AD∥BC,
∴∠2=∠3.
又∵BD平分∠ABC,
∴∠1=∠2,
∴∠1=∠3,
∴ AB =AD,
∴□ABCD是菱形.
17.【答案】 解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵AD平分∠BAC,
∴∠1=∠2(角平分线的定义),
∵DE∥AC,
∴∠2=∠3(两直线平行,内错角相等),
∴∠1=∠3(等量代换),
∴AE=DE,
∴平行四边形AEDF是菱形.
18.【答案】 解:∵AF∥CD, ∴∠AFE=∠CDE,
在△AFE和△CDE. ,
∴△AEF≌△CED, ∴AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形,
∵∠B=90°,∠ACB=30°, ∴∠CAB=60°,
∵AD平分∠CAB, ∴∠DAC=∠DAB=30°=∠ACD,
∴DA=DC, ∴四边形ADCF是菱形.
19.【答案】 解:四边形DBCE是菱形,理由如下:
DE垂直平分AC,
,
,即 ,
,
,
四边形DBCE是平行四边形,
, ,
是 的中位线,
点D是AB的中点,
,
又 在 中, ,
,
,
平行四边形DBCE是菱形.
四、综合题
20.【答案】 (1)证明:在Rt△ADB中,∵∠ADB=90°,AB=BE,
∴DB= AB=AB=BE,
∵DC∥BE,DC=AB=BE,
∴四边形BECD是平行四边形,
∵BD=BE,
∴四边形BECD是菱形.
(2)解:连接BC交DE于O.
∵四边形DBEC是菱形,
∴BC⊥DE,
∴BO∥AD,∵AB=BE,
∴DO=OE,
∴OB= AD=4,OD==2 ,
∴BC=8,DE=4 ,
∴S菱形BDCE= BC DE=16 .
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
