22.2 平行四边形课时训练(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第二十二章第二节平行四边形课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
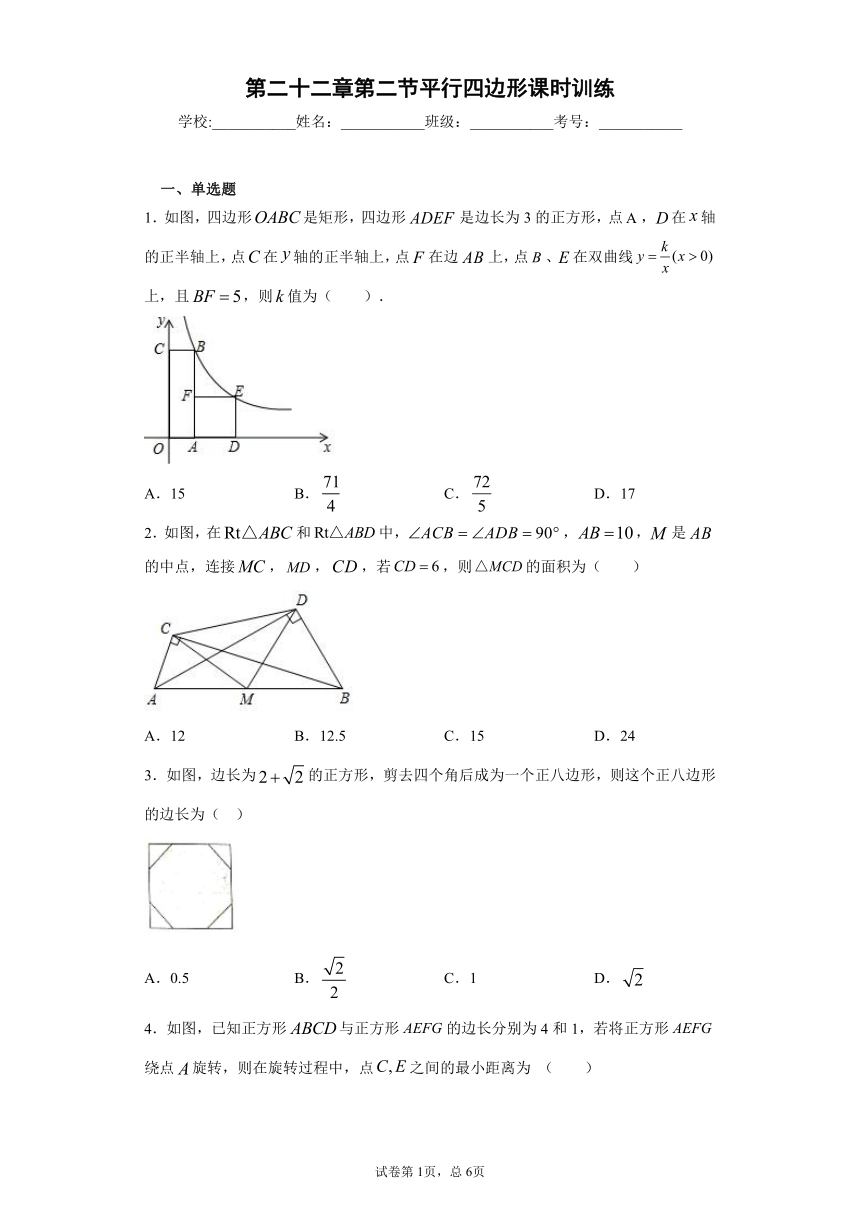
1.如图,四边形是矩形,四边形是边长为3的正方形,点,在轴的正半轴上,点在轴的正半轴上,点在边上,点、在双曲线上,且,则值为( ).
A.15 B. C. D.17
2.如图,在和中,,,是的中点,连接,,,若,则的面积为( )
A.12 B.12.5 C.15 D.24
3.如图,边长为的正方形,剪去四个角后成为一个正八边形,则这个正八边形的边长为( )
A.0.5 B. C.1 D.
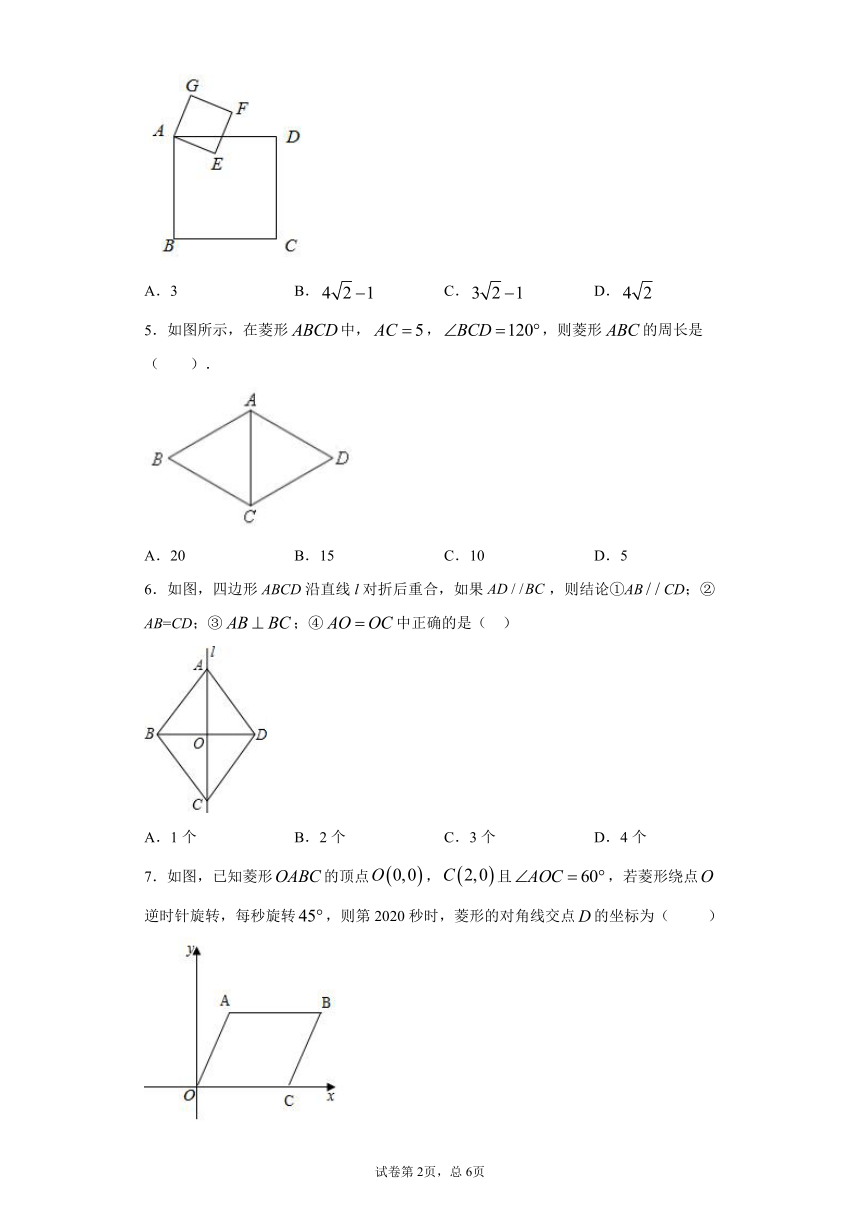
4.如图,已知正方形与正方形的边长分别为4和1,若将正方形绕点旋转,则在旋转过程中,点之间的最小距离为 ( )
A.3 B. C. D.
5.如图所示,在菱形中,,,则菱形的周长是( ).
A.20 B.15 C.10 D.5
6.如图,四边形ABCD沿直线l对折后重合,如果,则结论①ABCD;②AB=CD;③;④中正确的是( )
A.1个 B.2个 C.3个 D.4个
7.如图,已知菱形的顶点,且,若菱形绕点逆时针旋转,每秒旋转,则第2020秒时,菱形的对角线交点的坐标为( )
A. B.
C. D.
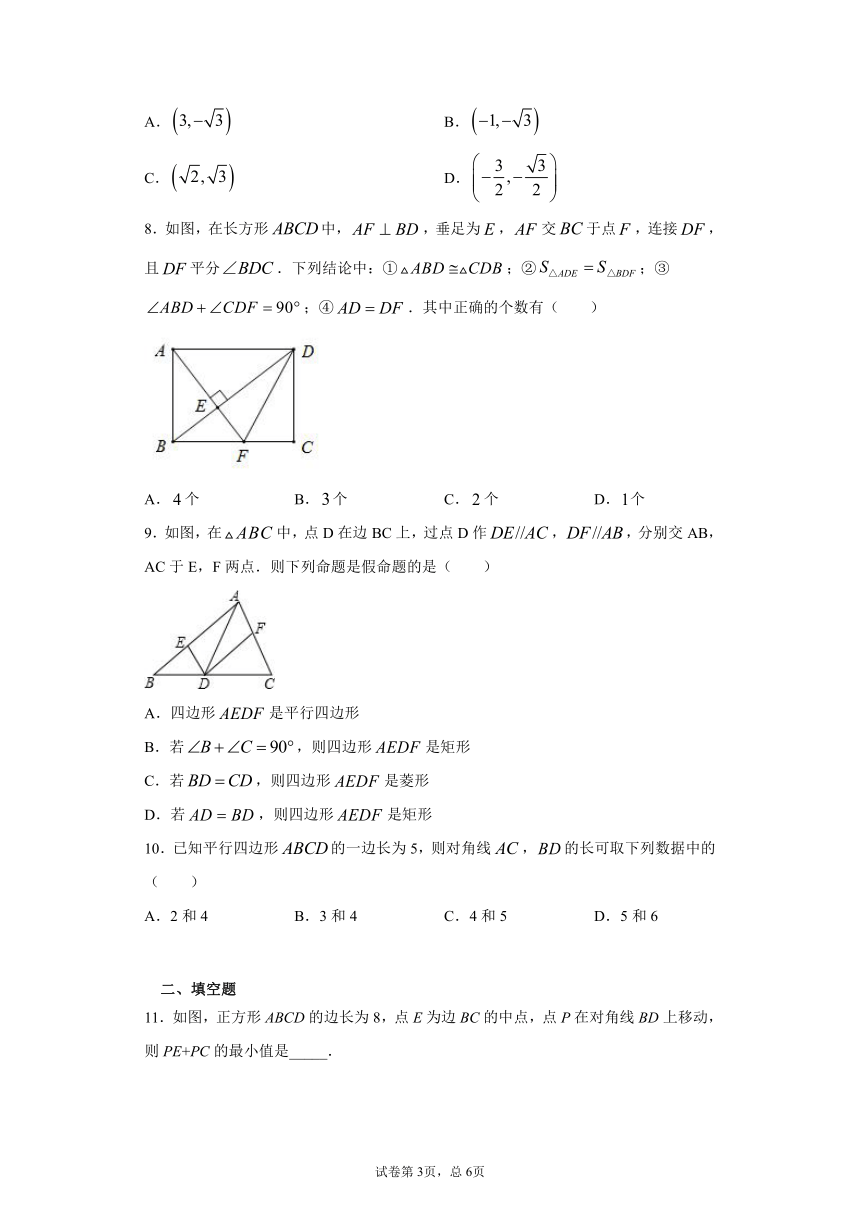
8.如图,在长方形中,,垂足为,交于点,连接,且平分.下列结论中:①;②;③;④.其中正确的个数有( )
A.个 B.个 C.个 D.个
9.如图,在中,点D在边BC上,过点D作,,分别交AB,AC于E,F两点.则下列命题是假命题的是( )
A.四边形是平行四边形
B.若,则四边形是矩形
C.若,则四边形是菱形
D.若,则四边形是矩形
10.已知平行四边形的一边长为5,则对角线,的长可取下列数据中的( )
A.2和4 B.3和4 C.4和5 D.5和6
二、填空题
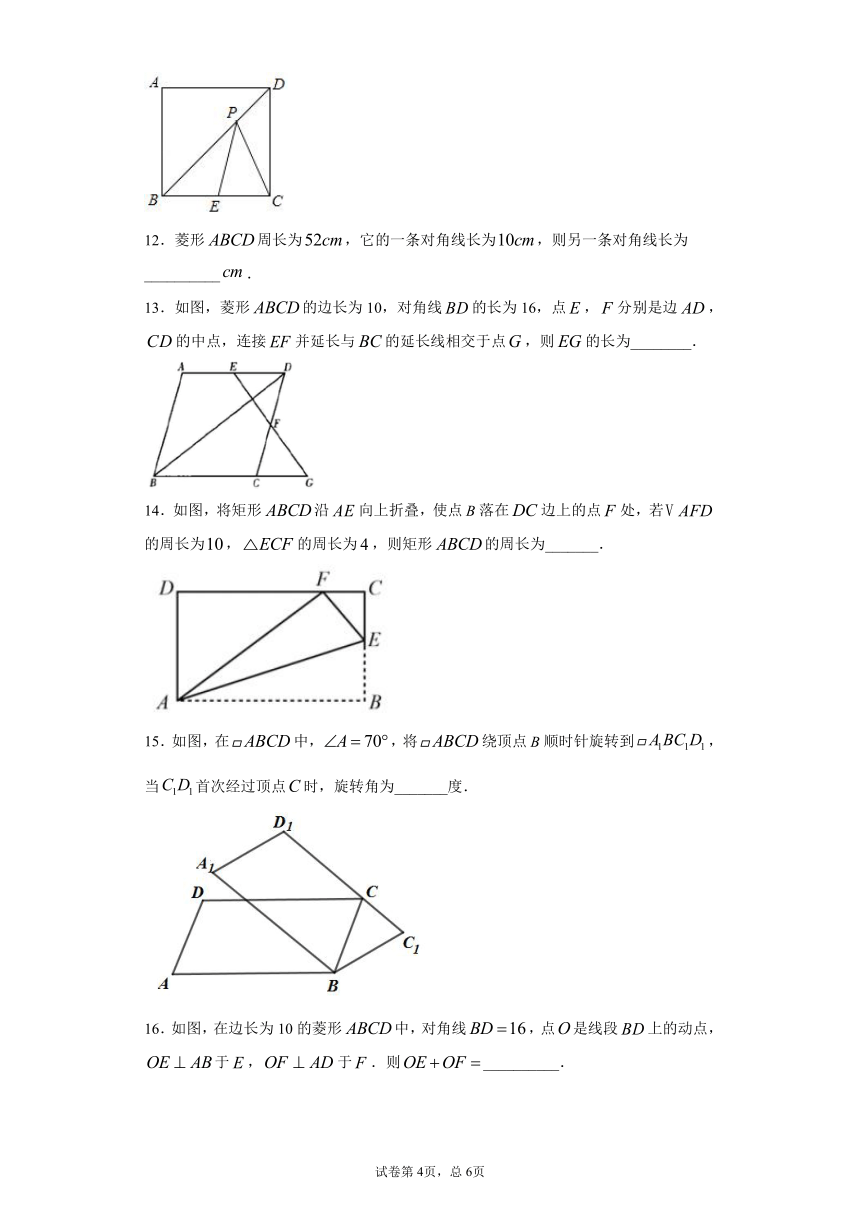
11.如图,正方形ABCD的边长为8,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是_____.
12.菱形周长为,它的一条对角线长为,则另一条对角线长为__________.
13.如图,菱形的边长为10,对角线的长为16,点,分别是边,的中点,连接并延长与的延长线相交于点,则的长为________.
14.如图,将矩形沿向上折叠,使点落在边上的点处,若的周长为,的周长为,则矩形的周长为_______.
15.如图,在中,,将绕顶点顺时针旋转到,当首次经过顶点时,旋转角为_______度.
16.如图,在边长为10的菱形中,对角线,点是线段上的动点,于,于.则__________.
三、解答题
17.如图,反比例函数的图象与一次函数相交于,,直线与轴,轴分别交于点,.
(1)求,的值;
(2)求出点坐标,再直接写出不等式的解集;
(3)点在函数的图象上,点在轴上,若以、、、为顶点的四边形是平行四边形,请你直接写出点坐标.
18.如图,是的中线,,且,连接,.
(1)求证:
(2)当满足什么条件时,四边形是矩形?并说明理由.
19.已知矩形中,点在边上,四边形是平行四边形,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹,不必写画法).
(1)在图画出中边上的中线;
(2)在图中画出线段的垂直平分线.
20.在中,,分别为对角线上两点,连接,,,,并且.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,若,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于面积的.
参考答案
1.C
2.A
3.D
4.B
5.A
6.C
7.D
8.C
9.C
10.D
11.4
12.24
13.12
14.
15.40
16.9.6
解:连接AC、OA,如图所示,
∵四边形ABCD为菱形,对角线,边长为10,
∴DG=8,AC⊥BD,
∴AG=,
∵,
即,
∴,
解得:OE+OF=9.6,
故答案为:9.6.
17.(1),;(2)B(-2,-3),或;(3),,
解:(1)把分别代入和得,
,
解得,
(2)由(1)知,,
∴直线AB的解析式为y=x-2,
将点B(n,-3)代入直线y=x-2中,得n-2=-3,
点坐标为
由图像可知,不等式的解集为:,
(3)由(2)知,直线AB的解析式为y=x-2,
当x=0时,y=-2,
∴D(0,-2),
当y=0时,x-2=0,
∴x=4,∴C(4,0),
由(1)知,k=6,
∴反比例函数的解析式为y=,
设点M(a,),N(b,0),
∵以C、D、M、N为顶点的四边形是平行四边形,
①当CD与MN为对角线时,(0+4)=(a+b),(-2+0)=(+0),
∴a=-3,b=7,
∴N(7,0),
②当CM与DN为对角线时,(a+4)=(0+b),(+0)=(-2+0),
∴a=-3,b=1,
∴N(1,0),
③当CN与DM为对角线时,(b+4)=(a+0),(0+0)=(-2),
∴a=3,b=-1,
∴N(-1,0),
即满足条件的点N的坐标为(1,0)、(7,0)、(-1,0)
18.(1)证明见解析;(2)当满足时,四边形是矩形,证明见解析
(1)是的中线
又
四边形是平行四边形
(2)当满足时,四边形是矩形
,
又
四边形是平行四边形
当时,
四边形是矩形
19.(1)见解析 (2)见解析
解:(1)如图,延长交于,连结,交于N,连结AH,FB交于M
过M、N作直线交DC于G
连结BG
如图,线段即为所求作;
(2)如图,连接 ,相交于M,连接BE并交AD于N,
∵四边形是平行四边形,矩形
∴EF=CD=AB,EF∥CD∥AB
∴∠ABN=∠FEN,∠ANB=∠FNE
∴△ANB≌△FNE(AAS)
∴AN=FN
过M、N作直线l
如图,直线即为所求作.
20.(1)见解析;(2),,,
(1)证明:如图1,
∵四边形为平行四边形,
∴,,
∵,
∴,
∴,即,
∴,
∴,
∴四边形是平行四边形;
(2)由(1)可得,BE=DF,
∵,
∴,
根据△ABD和△ABE、△ADF是等高,可得:△ABE、△ADF的面积是△ABD面积的,
∵四边形ABCD是平行四边形,
∴△ABD和△BCD的面积相等,
同理可得△BEC和△DFC的面积是△BCD面积的,
∴,,,的面积都等于面积的.
试卷第6 66页,总6 66页
_21?????????è?????(www.21cnjy.com)_
第二十二章第二节平行四边形课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,四边形是矩形,四边形是边长为3的正方形,点,在轴的正半轴上,点在轴的正半轴上,点在边上,点、在双曲线上,且,则值为( ).
A.15 B. C. D.17
2.如图,在和中,,,是的中点,连接,,,若,则的面积为( )
A.12 B.12.5 C.15 D.24
3.如图,边长为的正方形,剪去四个角后成为一个正八边形,则这个正八边形的边长为( )
A.0.5 B. C.1 D.
4.如图,已知正方形与正方形的边长分别为4和1,若将正方形绕点旋转,则在旋转过程中,点之间的最小距离为 ( )
A.3 B. C. D.
5.如图所示,在菱形中,,,则菱形的周长是( ).
A.20 B.15 C.10 D.5
6.如图,四边形ABCD沿直线l对折后重合,如果,则结论①ABCD;②AB=CD;③;④中正确的是( )
A.1个 B.2个 C.3个 D.4个
7.如图,已知菱形的顶点,且,若菱形绕点逆时针旋转,每秒旋转,则第2020秒时,菱形的对角线交点的坐标为( )
A. B.
C. D.
8.如图,在长方形中,,垂足为,交于点,连接,且平分.下列结论中:①;②;③;④.其中正确的个数有( )
A.个 B.个 C.个 D.个
9.如图,在中,点D在边BC上,过点D作,,分别交AB,AC于E,F两点.则下列命题是假命题的是( )
A.四边形是平行四边形
B.若,则四边形是矩形
C.若,则四边形是菱形
D.若,则四边形是矩形
10.已知平行四边形的一边长为5,则对角线,的长可取下列数据中的( )
A.2和4 B.3和4 C.4和5 D.5和6
二、填空题
11.如图,正方形ABCD的边长为8,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是_____.
12.菱形周长为,它的一条对角线长为,则另一条对角线长为__________.
13.如图,菱形的边长为10,对角线的长为16,点,分别是边,的中点,连接并延长与的延长线相交于点,则的长为________.
14.如图,将矩形沿向上折叠,使点落在边上的点处,若的周长为,的周长为,则矩形的周长为_______.
15.如图,在中,,将绕顶点顺时针旋转到,当首次经过顶点时,旋转角为_______度.
16.如图,在边长为10的菱形中,对角线,点是线段上的动点,于,于.则__________.
三、解答题
17.如图,反比例函数的图象与一次函数相交于,,直线与轴,轴分别交于点,.
(1)求,的值;
(2)求出点坐标,再直接写出不等式的解集;
(3)点在函数的图象上,点在轴上,若以、、、为顶点的四边形是平行四边形,请你直接写出点坐标.
18.如图,是的中线,,且,连接,.
(1)求证:
(2)当满足什么条件时,四边形是矩形?并说明理由.
19.已知矩形中,点在边上,四边形是平行四边形,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹,不必写画法).
(1)在图画出中边上的中线;
(2)在图中画出线段的垂直平分线.
20.在中,,分别为对角线上两点,连接,,,,并且.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,若,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于面积的.
参考答案
1.C
2.A
3.D
4.B
5.A
6.C
7.D
8.C
9.C
10.D
11.4
12.24
13.12
14.
15.40
16.9.6
解:连接AC、OA,如图所示,
∵四边形ABCD为菱形,对角线,边长为10,
∴DG=8,AC⊥BD,
∴AG=,
∵,
即,
∴,
解得:OE+OF=9.6,
故答案为:9.6.
17.(1),;(2)B(-2,-3),或;(3),,
解:(1)把分别代入和得,
,
解得,
(2)由(1)知,,
∴直线AB的解析式为y=x-2,
将点B(n,-3)代入直线y=x-2中,得n-2=-3,
点坐标为
由图像可知,不等式的解集为:,
(3)由(2)知,直线AB的解析式为y=x-2,
当x=0时,y=-2,
∴D(0,-2),
当y=0时,x-2=0,
∴x=4,∴C(4,0),
由(1)知,k=6,
∴反比例函数的解析式为y=,
设点M(a,),N(b,0),
∵以C、D、M、N为顶点的四边形是平行四边形,
①当CD与MN为对角线时,(0+4)=(a+b),(-2+0)=(+0),
∴a=-3,b=7,
∴N(7,0),
②当CM与DN为对角线时,(a+4)=(0+b),(+0)=(-2+0),
∴a=-3,b=1,
∴N(1,0),
③当CN与DM为对角线时,(b+4)=(a+0),(0+0)=(-2),
∴a=3,b=-1,
∴N(-1,0),
即满足条件的点N的坐标为(1,0)、(7,0)、(-1,0)
18.(1)证明见解析;(2)当满足时,四边形是矩形,证明见解析
(1)是的中线
又
四边形是平行四边形
(2)当满足时,四边形是矩形
,
又
四边形是平行四边形
当时,
四边形是矩形
19.(1)见解析 (2)见解析
解:(1)如图,延长交于,连结,交于N,连结AH,FB交于M
过M、N作直线交DC于G
连结BG
如图,线段即为所求作;
(2)如图,连接 ,相交于M,连接BE并交AD于N,
∵四边形是平行四边形,矩形
∴EF=CD=AB,EF∥CD∥AB
∴∠ABN=∠FEN,∠ANB=∠FNE
∴△ANB≌△FNE(AAS)
∴AN=FN
过M、N作直线l
如图,直线即为所求作.
20.(1)见解析;(2),,,
(1)证明:如图1,
∵四边形为平行四边形,
∴,,
∵,
∴,
∴,即,
∴,
∴,
∴四边形是平行四边形;
(2)由(1)可得,BE=DF,
∵,
∴,
根据△ABD和△ABE、△ADF是等高,可得:△ABE、△ADF的面积是△ABD面积的,
∵四边形ABCD是平行四边形,
∴△ABD和△BCD的面积相等,
同理可得△BEC和△DFC的面积是△BCD面积的,
∴,,,的面积都等于面积的.
试卷第6 66页,总6 66页
_21?????????è?????(www.21cnjy.com)_
