2020-2021学年人教版七年级数学下册 9.3.1 解一元一次不等式组 课件(62张)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册 9.3.1 解一元一次不等式组 课件(62张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 00:00:00 | ||
图片预览










文档简介
(共62张PPT)
第九章
9.3.1
解一元一次不等式组
人教版数学七年级下册
1.理解一元一次不等式组的概念.
2.理解不等式组的解的概念.
3.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解.
学习目标
要小于6
要大于
3
不等式组
一元一次不等式组
学习目标
1
知识点
一元一次不等组
问题
用每分可抽30
t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200
t而不足1500
t,那么将污水抽完所用时间的范围是什么?
设用x
min能将污水抽完,则x同时满足不等式
30x>1200,
①
30x<1500
.
②
合作探究
类似于方程组,把这两个不等式合起来,组成
一个一元一次不等式组,记作
一般地,关于同一未知数的几个一元一次不
等式合在一起,就组成一个一元一次不等式
组.
定义
如何判定一元一次方程组:
(1)这里的“几个”是指两个或两个以上;
(2)每个不等式只能是一元一次不等式;
(3)每个不等式必须含有同一个未知数.
下列各不等式组,其中是一元一次不等式组的有________.(填序号)
①
②
③
④
⑤
⑥
例1
③④⑤
导引:
紧扣一元一次不等式组的定义去识别:①中含有
两个未知数;②中未知数的最高次数是2;⑥中
不是整式.
判定一个不等式组是一元一次不等式组,要从以
下两个方面考虑:
(1)组成不等式组的每个不等式必须是一元一次不等式;
(2)这个不等式组中只含有一个未知数.
新知小结
1 下列各不等式组,其中是一元一次不等式组的有____________(填序号).
③④⑤
巩固新知
2
知识点
一元一次不等式组的解集
怎样确定不等式组中x的可取值的范围呢?
类比方程组的解,不等式组中的各不等式解集
的公共部分,就是不等式组中x可以取值的范围.
由不等式①,解得
x>40.
由不等式②,解得x<50.
合作探究
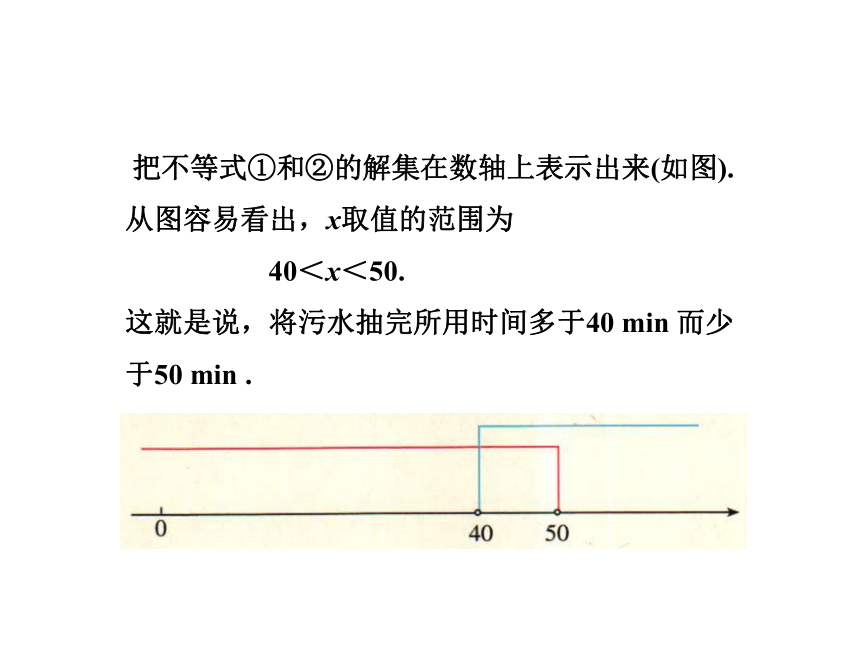
把不等式①和②的解集在数轴上表示出来(如图).
从图容易看出,x取值的范围为
40<x<50.
这就是说,将污水抽完所用时间多于40
min
而少
于50
min
.
一般地,几个不等式的解集的公共部分,叫
做由它们所组成的不等式组的解集.
解不等式组就是求它的解集
.
探索不等式组
的解集与组成它的不等式①
、②的解集有什么联系?
-2
-1
0
1
2
3
4
5
6
在同一数轴上分别表示出不等式①
、②的解集.
公共部分
这个不等式组的解集为3≤x<5.
注意:
在数轴上表示不等式的解集时应注意:
大于向右画,小于向左画;有等号的画实心圆点,无等号的画空心圆圈.
利用数轴求下列不等式组的解集:
(1)
(2)
(3)
(4)
例2
导引:
解题时先在同一数轴上表示出各不等式组中两
个不等式的解集,再找出两个不等式解集的公
共部分.
解:
(1)两个不等式的解集在数轴上的表示如图1所示.
所以这个不等式组的解集为x≥2.
(2)两个不等式的解集在数轴上的表示如图2所示.
所以这个不等式组的解集为x<-1.
图1
图2
(3)两个不等式的解集在数轴上的表示如图3所示.
所以这个不等式组无解.
(4)两个不等式的解集在数轴上的表示如图4所示.
所以这个不等式组的解集为-1<x≤2.
图3
图4
确定一元一次不等式组解集的常用方法:
(1)数轴法:就是将几个不等式的解集在同一数轴上表
示出来,然后找出它们的公共部分,这个公共部分
就是此不等式组的解集;如果没有公共部分,那么
这个不等式组无解.这种方法体现了数形结合思想,
既直观又明了,易于掌握.
(2)口诀法:“同大取大”“同小取小”“大小小大中
间找”“大大小小无处找”,该方法便于记忆.
新知小结
1
不等式组
的解集是( )
A.x<1
B.x≥3
C.1≤x<3
D.1<x≤3
D
巩固新知
3
知识点
一元一次不等式组的解法
1.定义:求不等式组的解集的过程叫做解不等式组.
2.解一元一次不等式组的一般步骤:
(1)分别解每一个不等式;
(2)利用数轴法或口诀法确定不等式组的解集;
(3)写出不等式组的解集.
合作探究
解下列不等式组:
例3
解:
(1)解不等式①,得
x>2.
解不等式②,得
x>3.
把不等式①和②的解集在数轴上表示出来(如图).
从上图可以找出两个不等式解集的公共部分,得不
等式组的解集x>3.
(2)解不等式①,得
x≥8.
解不等式②,得
x<
把不等式①和②的解集在数轴上表示出来(如图).
从上图可以看到这两个不等式的解集没有公共部分,
不等式组无解.
解不等式组的关键:一是要正确地求出每个不等
式的解集;二是要利用数轴正确地表示出每个不等式
的解集,并找出不等式组的解集.
新知小结
1
解下列不等式组:
巩固新知
解:
解不等式①,得x>
,解不等式②,得x>1,
所以原不等式组的解集为x>1.
解不等式①,得x<-6,解不等式②,得x≥2.
所以不等式组无解.
解不等式①,得x>-
,
解不等式②,得x≤
.
所以原不等式组的解集为-
.
2
x取哪些正整数值时,不等式x+3>6与2x-1<10都成立?
解:
解不等式组
得3,
所以x可取的正整数值是4,5.
【中考·深圳】不等式组
的解集为( )
A.x>-1
B.x<3
C.x<-1或x>3
D.-13
D
不等式组
的最大整数解为
( )
A.8
B.6
C.5
D.4
4
C
【中考·孝感】不等式组
的解集在数轴上表示正确的是( )
5
D
【中考·宿迁】已知4的整数解共有( )
A.1个
B.2个
C.3个
D.4个
6
B
【中考·金华】若关于x的一元一次不等式组
的解集是x<5,则m的取值范围是( )
A.m≥5
B.m>5
C.m≤5
D.m<5
7
A
1.一元一次不等式组的基本概念:
(1)一元一次不等式组的定义;
(2)一元一次不等式组的解集;
(3)解一元一次不等式组.
2.一元一次不等式组的解法:
(1)分别解每一个不等式;
(2)利用数轴法或口诀法确定不等式组的解集;
(3)写出不等式组的解集.
1
知识小结
归纳新知
【中考?绥化】关于x的不等式组
的解集为x>1,
则a的取值范围是( )
A.a>1
B.a<1
C.a≥1
D.a≤1
易错点:运用解集求原不等式组中字母的取值范围时易忽略等号
2
易错小结
D
此题学生容易遗漏a=1的情况而错选B.
1.一元一次不等式组包含三个条件:
(1)不等式组中所有的不等式都是__________不等式;
(2)所有一元一次不等式都含有________________________;
(3)不等式组中的一元一次不等式至少有_____个.
一元一次
同一个未知数
两
课后练习
D
3.一元一次不等式组中各个不等式的解集的___________,叫做这个一元一次不等式组的解集.
公共部分
x>a
D
6.求不等式组解集的过程,叫做______________.
解一元一次不等式组通常用“分开解,集中判”的方法.
“分开解”就是分别求出不等式组中各个_______________,并在同一数轴上表示出来;“集中判”是取各个不等式的解集的_______________,即可求得不等式组的解集.
解不等式组
不等式的解集
公共部分
D
【点拨】分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,找出整数解即可.
B
D
【点拨】解不等式x-m<0,得x2(x-1),得x>-1.
因为不等式组无解,所以m≤-1.
A
C
【答案】B
(1)解不等式①,得________;
(2)解不等式②,得________;
x≤1
x≥-3
(4)原不等式组的解集为_____________.
解:把不等式①和②的解集在数轴上表示出来如图.
(3)把不等式①和②的解集在数轴(如图)上表示出来;
-3≤x≤1.
由(1)得x>2,由(2)得x<-3,
∴原不等式的解集为x<-3或x>2.
请你运用所学知识,结合上述材料解答下列问题:
(1)不等式x2-2x-3<0的解集为____________.
【思路点拨】解题的关键是先要读懂材料部分的含义,学会其方法,然后利用学到的方法,把所面对的特殊不等式转化为学过的一元一次不等式组来解决.
-1<x<3
再见
第九章
9.3.1
解一元一次不等式组
人教版数学七年级下册
1.理解一元一次不等式组的概念.
2.理解不等式组的解的概念.
3.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解.
学习目标
要小于6
要大于
3
不等式组
一元一次不等式组
学习目标
1
知识点
一元一次不等组
问题
用每分可抽30
t水的抽水机来抽污水管道里积存的污水,估计积存的污水超过1200
t而不足1500
t,那么将污水抽完所用时间的范围是什么?
设用x
min能将污水抽完,则x同时满足不等式
30x>1200,
①
30x<1500
.
②
合作探究
类似于方程组,把这两个不等式合起来,组成
一个一元一次不等式组,记作
一般地,关于同一未知数的几个一元一次不
等式合在一起,就组成一个一元一次不等式
组.
定义
如何判定一元一次方程组:
(1)这里的“几个”是指两个或两个以上;
(2)每个不等式只能是一元一次不等式;
(3)每个不等式必须含有同一个未知数.
下列各不等式组,其中是一元一次不等式组的有________.(填序号)
①
②
③
④
⑤
⑥
例1
③④⑤
导引:
紧扣一元一次不等式组的定义去识别:①中含有
两个未知数;②中未知数的最高次数是2;⑥中
不是整式.
判定一个不等式组是一元一次不等式组,要从以
下两个方面考虑:
(1)组成不等式组的每个不等式必须是一元一次不等式;
(2)这个不等式组中只含有一个未知数.
新知小结
1 下列各不等式组,其中是一元一次不等式组的有____________(填序号).
③④⑤
巩固新知
2
知识点
一元一次不等式组的解集
怎样确定不等式组中x的可取值的范围呢?
类比方程组的解,不等式组中的各不等式解集
的公共部分,就是不等式组中x可以取值的范围.
由不等式①,解得
x>40.
由不等式②,解得x<50.
合作探究
把不等式①和②的解集在数轴上表示出来(如图).
从图容易看出,x取值的范围为
40<x<50.
这就是说,将污水抽完所用时间多于40
min
而少
于50
min
.
一般地,几个不等式的解集的公共部分,叫
做由它们所组成的不等式组的解集.
解不等式组就是求它的解集
.
探索不等式组
的解集与组成它的不等式①
、②的解集有什么联系?
-2
-1
0
1
2
3
4
5
6
在同一数轴上分别表示出不等式①
、②的解集.
公共部分
这个不等式组的解集为3≤x<5.
注意:
在数轴上表示不等式的解集时应注意:
大于向右画,小于向左画;有等号的画实心圆点,无等号的画空心圆圈.
利用数轴求下列不等式组的解集:
(1)
(2)
(3)
(4)
例2
导引:
解题时先在同一数轴上表示出各不等式组中两
个不等式的解集,再找出两个不等式解集的公
共部分.
解:
(1)两个不等式的解集在数轴上的表示如图1所示.
所以这个不等式组的解集为x≥2.
(2)两个不等式的解集在数轴上的表示如图2所示.
所以这个不等式组的解集为x<-1.
图1
图2
(3)两个不等式的解集在数轴上的表示如图3所示.
所以这个不等式组无解.
(4)两个不等式的解集在数轴上的表示如图4所示.
所以这个不等式组的解集为-1<x≤2.
图3
图4
确定一元一次不等式组解集的常用方法:
(1)数轴法:就是将几个不等式的解集在同一数轴上表
示出来,然后找出它们的公共部分,这个公共部分
就是此不等式组的解集;如果没有公共部分,那么
这个不等式组无解.这种方法体现了数形结合思想,
既直观又明了,易于掌握.
(2)口诀法:“同大取大”“同小取小”“大小小大中
间找”“大大小小无处找”,该方法便于记忆.
新知小结
1
不等式组
的解集是( )
A.x<1
B.x≥3
C.1≤x<3
D.1<x≤3
D
巩固新知
3
知识点
一元一次不等式组的解法
1.定义:求不等式组的解集的过程叫做解不等式组.
2.解一元一次不等式组的一般步骤:
(1)分别解每一个不等式;
(2)利用数轴法或口诀法确定不等式组的解集;
(3)写出不等式组的解集.
合作探究
解下列不等式组:
例3
解:
(1)解不等式①,得
x>2.
解不等式②,得
x>3.
把不等式①和②的解集在数轴上表示出来(如图).
从上图可以找出两个不等式解集的公共部分,得不
等式组的解集x>3.
(2)解不等式①,得
x≥8.
解不等式②,得
x<
把不等式①和②的解集在数轴上表示出来(如图).
从上图可以看到这两个不等式的解集没有公共部分,
不等式组无解.
解不等式组的关键:一是要正确地求出每个不等
式的解集;二是要利用数轴正确地表示出每个不等式
的解集,并找出不等式组的解集.
新知小结
1
解下列不等式组:
巩固新知
解:
解不等式①,得x>
,解不等式②,得x>1,
所以原不等式组的解集为x>1.
解不等式①,得x<-6,解不等式②,得x≥2.
所以不等式组无解.
解不等式①,得x>-
,
解不等式②,得x≤
.
所以原不等式组的解集为-
2
x取哪些正整数值时,不等式x+3>6与2x-1<10都成立?
解:
解不等式组
得3
所以x可取的正整数值是4,5.
【中考·深圳】不等式组
的解集为( )
A.x>-1
B.x<3
C.x<-1或x>3
D.-1
D
不等式组
的最大整数解为
( )
A.8
B.6
C.5
D.4
4
C
【中考·孝感】不等式组
的解集在数轴上表示正确的是( )
5
D
【中考·宿迁】已知4
A.1个
B.2个
C.3个
D.4个
6
B
【中考·金华】若关于x的一元一次不等式组
的解集是x<5,则m的取值范围是( )
A.m≥5
B.m>5
C.m≤5
D.m<5
7
A
1.一元一次不等式组的基本概念:
(1)一元一次不等式组的定义;
(2)一元一次不等式组的解集;
(3)解一元一次不等式组.
2.一元一次不等式组的解法:
(1)分别解每一个不等式;
(2)利用数轴法或口诀法确定不等式组的解集;
(3)写出不等式组的解集.
1
知识小结
归纳新知
【中考?绥化】关于x的不等式组
的解集为x>1,
则a的取值范围是( )
A.a>1
B.a<1
C.a≥1
D.a≤1
易错点:运用解集求原不等式组中字母的取值范围时易忽略等号
2
易错小结
D
此题学生容易遗漏a=1的情况而错选B.
1.一元一次不等式组包含三个条件:
(1)不等式组中所有的不等式都是__________不等式;
(2)所有一元一次不等式都含有________________________;
(3)不等式组中的一元一次不等式至少有_____个.
一元一次
同一个未知数
两
课后练习
D
3.一元一次不等式组中各个不等式的解集的___________,叫做这个一元一次不等式组的解集.
公共部分
x>a
D
6.求不等式组解集的过程,叫做______________.
解一元一次不等式组通常用“分开解,集中判”的方法.
“分开解”就是分别求出不等式组中各个_______________,并在同一数轴上表示出来;“集中判”是取各个不等式的解集的_______________,即可求得不等式组的解集.
解不等式组
不等式的解集
公共部分
D
【点拨】分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,找出整数解即可.
B
D
【点拨】解不等式x-m<0,得x
因为不等式组无解,所以m≤-1.
A
C
【答案】B
(1)解不等式①,得________;
(2)解不等式②,得________;
x≤1
x≥-3
(4)原不等式组的解集为_____________.
解:把不等式①和②的解集在数轴上表示出来如图.
(3)把不等式①和②的解集在数轴(如图)上表示出来;
-3≤x≤1.
由(1)得x>2,由(2)得x<-3,
∴原不等式的解集为x<-3或x>2.
请你运用所学知识,结合上述材料解答下列问题:
(1)不等式x2-2x-3<0的解集为____________.
【思路点拨】解题的关键是先要读懂材料部分的含义,学会其方法,然后利用学到的方法,把所面对的特殊不等式转化为学过的一元一次不等式组来解决.
-1<x<3
再见
