2020-2021学年下学期初中数学人教版八年级 平行四边形 单元检测题 (Word版含答案)
文档属性
| 名称 | 2020-2021学年下学期初中数学人教版八年级 平行四边形 单元检测题 (Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 198.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 00:00:00 | ||
图片预览



文档简介
2020-2021学年下学期初中数学
人教版八年级 平行四边形 单元检测题
__ 班级:__________ 姓名:__________ 考号:__________
?
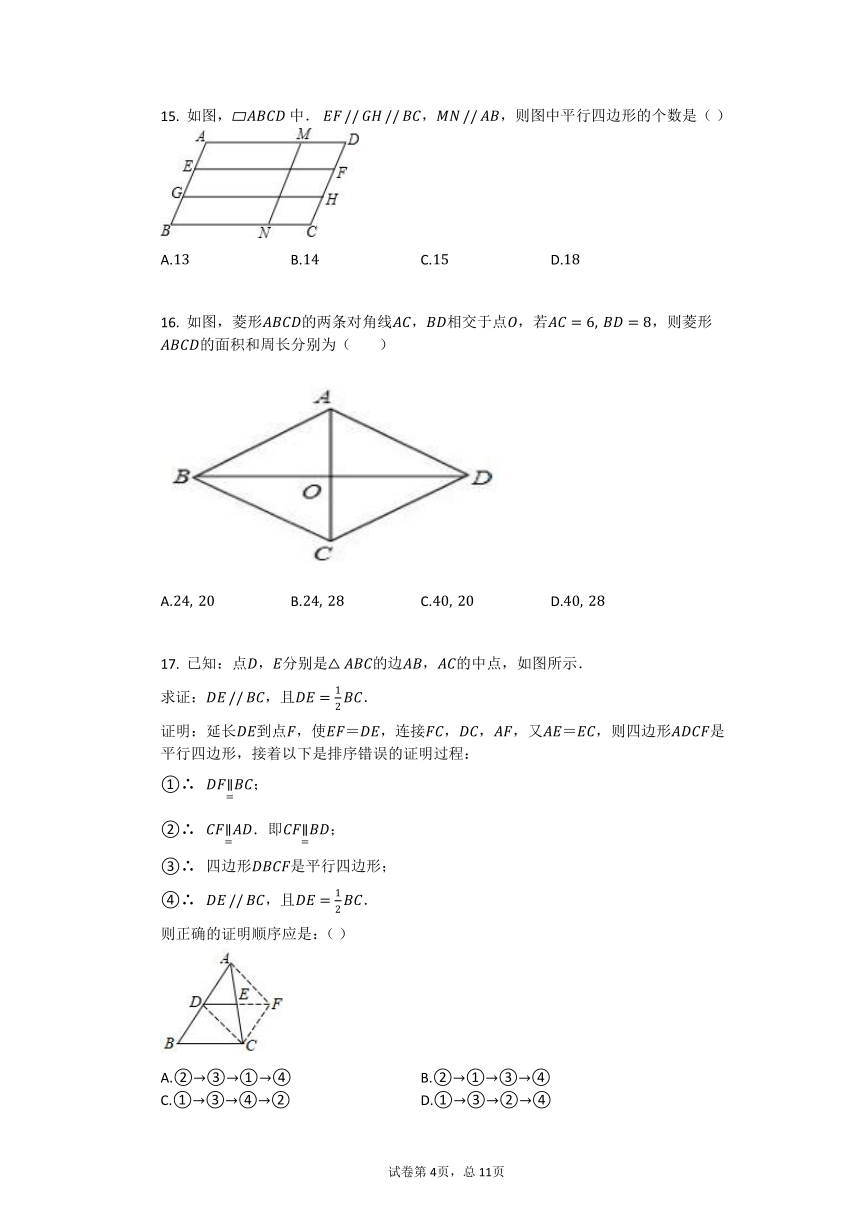
1. 闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB?//?EF?//?DC,BC?//?GH?//?AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )
A.球落在红花丛中和绿花丛中的概率相等
B.球落在紫花丛中和橙花丛中的概率相等
C.球落在红花丛中和蓝花丛中的概率相等
D.球落在蓝花丛中和黄花丛中的概率相等
?
2. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )
A.2 B.22 C.2 D.1
?
3. 如图,直线,P是直线AB上的动点,当点P的位置变化时,三角形PCD的面积将
A.变小
B.变大
C.不变
D.变大变小要看点P向左还是向右移动
?
4. 如图,在矩形ABCD中,AD=6,对角线AC与BD交于点O,AE⊥BD,垂足为点E,且AE平分∠BAO,则AB的长为( )
A.3 B.4 C.23 D.33
?
5. 如图,AE?//?BD,BE?//?DF,AB?//?CD,下面给出四个结论:
(1)四边形ABDC是平行四边形;(2)BE=DF;(3)SABDC=SBDFE;(4)BD=CE.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
?
6. 下列命题正确的是( )
A.对角线相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的平行四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
?
7. 如图,在平行四边形ABCD中,P是AB上一点,E,F分别是BC,AD的中点,连接PE,PC,PD,PF.设平行四边形ABCD的面积为m,则S△PCE+S△PDF=(? ? ? ??)
?
A.14m B.13m C.12m D.35m
?
8. 下列说法中错误的是(? ? ? ? )
A.直角三角形斜边上的中线等于斜边的一半
B.菱形的对角线平分一组对角,并且菱形是轴对称图形
C.矩形的对角线把这个矩形分成4个等腰三角形
D.对角线互相垂直的菱形是正方形
?
9. 如图,?ABCD的对角线AC上有一点P,过P点作HG?//?AB,过P点作MN?//?AD,图中面积相等的平行四边形有几对?(? ? ? ? )
A.1对 B.2对 C.3对 D.4对
?
10. 能判别一个四边形是正方形的条件是( )
A.对角线相等,对边平行且相等
B.一组对边平行,一组对角相等
C.对角线互相垂直平分且相等
D.一组邻边相等,对角线互相平分
?
11. 如图所示,在四边形ABCD中,AD?//?BC,要使四边形ABCD成为平行四边形还需要条件(? ? ? ? )
A.AB=DC B.∠1=∠2 C.AB=AD D.∠D=∠B
?
12. 根据下列条件,能判定平行四边形ABCD是矩形的是(????????)
A.AB=CD,AD=BC B.AB=BC
C.AC=BD D.AB?//?CD,AD?//?BC
?
13. 已知四边形ABCD中,AB?//?CD.则添加下列条件,不能使四边形ABCD成为平行四边形的是( )
A.AB=CD B.∠B=∠D C.AD?//?BC D.AD=BC
?
14. 《几何原本》是古希朋数学家所著的一部数学著作,共13卷,这本著作是现代数学的基础,在西方是仅次于《圣经》而流传最广的书籍.这位古希腊数学家是(????????)
A.利玛窦 B.高斯 C.李善兰 D.欧几里得
?
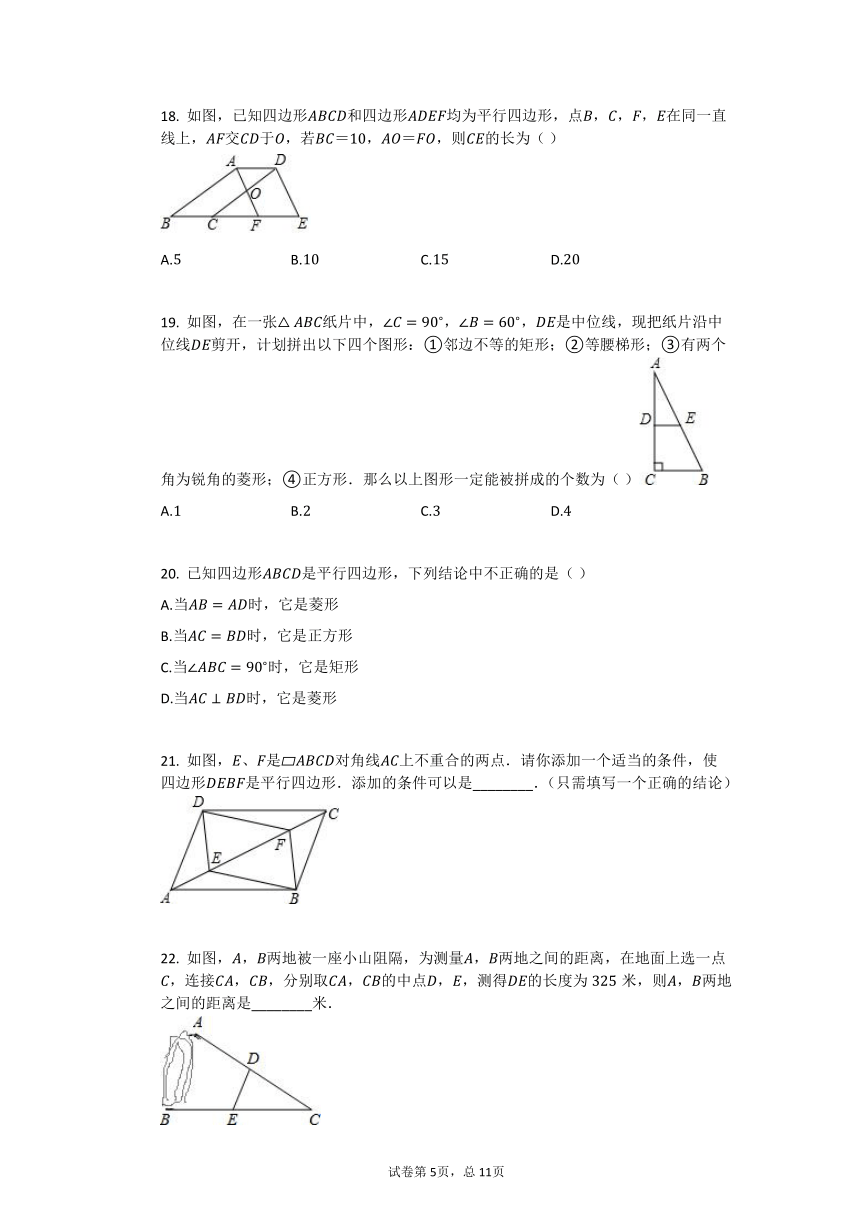
15. 如图,?ABCD?中.?EF?//?GH?//?BC,MN?//?AB,则图中平行四边形的个数是( )
A.13 B.14 C.15 D.18
?
16. 如图,菱形ABCD的两条对角线AC,BD相交于点O,若AC=6,?BD=8,则菱形ABCD的面积和周长分别为(? ? ? ? )
A.24,?20 B.24,?28 C.40,?20 D.40,?28
?
17. 已知:点D,E分别是△ABC的边AB,AC的中点,如图所示.
求证:DE?//?BC,且DE=12BC.
证明:延长DE到点F,使EF=DE,连接FC,DC,AF,又AE=EC,则四边形ADCF是平行四边形,接着以下是排序错误的证明过程:
①∴ DF∥=BC;
②∴ CF∥=AD.即CF∥=BD;
③∴ 四边形DBCF是平行四边形;
④∴ DE?//?BC,且DE=12BC.
则正确的证明顺序应是:( )
A.②→③→①→④ B.②→①→③→④
C.①→③→④→② D.①→③→②→④
?
18. 如图,已知四边形ABCD和四边形ADEF均为平行四边形,点B,C,F,E在同一直线上,AF交CD于O,若BC=10,AO=FO,则CE的长为( )
A.5 B.10 C.15 D.20
?
19. 如图,在一张△ABC纸片中,∠C=90?,∠B=60?,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
A.1 B.2 C.3 D.4
?
20. 已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=AD时,它是菱形
B.当AC=BD时,它是正方形
C.当∠ABC=90?时,它是矩形
D.当AC⊥BD时,它是菱形
?
21. 如图,E、F是?ABCD对角线AC上不重合的两点.请你添加一个适当的条件,使四边形DEBF是平行四边形.添加的条件可以是________.(只需填写一个正确的结论)
?
22. 如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D,E,测得DE的长度为325米,则A,B两地之间的距离是________米.
?
23. 如图,在矩形ABCD中,AB=3,BC=8,四边形ECGF为菱形,点G在AD上,点B在EF上,若菱形的一条对角线CF=45,则菱形ECGF的另一条对角线EG的长度是__________.
?
24. 若直角三角形斜边长为6cm,则斜边上的中线长为________cm.
?
25. 在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.你添加的条件是________.?(写出一种即可)
?
26. 如图:已知四边形ABCD,∠A、∠B、∠C都是直角.求证:四边形ABCD是矩形.
?
27. 如图:菱形ABCD的边长为2,∠BAD=120?,对角线AC、BD相交于O,求菱形ABCD的面积.
?
28. 如图,在△ABC中,∠ACB=90?,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE,AF.
(1)求证:AF=CE;
(2)当∠B=30?时,试判断四边形ACEF的形状,并说明理由.
?
29. 如图,已知△ABC中,BD平分∠ABC,点M是BD上一点,过M点作EF?//?BC,分别交AB、AC于E、F,作MN?//?AB交BC于N.
(1)试判断四边形BEMN是什么特殊四边形?并证明你的结论.
(2)连接EN,将△ABC再添加一个什么条件时,四边形EFCN是平行四边形?
?
30. 如图6,在平行四边形ABCD中,?AE⊥BC,AF⊥CD?,垂足分别为 E,F,BE=DF.?
(1)求证:平行四边形ABCD是菱形;
(2)若 AB=5,?AC=6,求四边形ABCD的面积.
参考答案与试题解析
一、 选择题 (本题共计 20 小题 ,每题 3 分 ,共计60分 )
1.
【答案】
C
2.
【答案】
B
3.
【答案】
C
4.
【答案】
C
5.
【答案】
B
6.
【答案】
C
7.
【答案】
A
8.
【答案】
D
9.
【答案】
C
10.
【答案】
C
11.
【答案】
D
12.
【答案】
C
13.
【答案】
D
14.
【答案】
D
15.
【答案】
D
16.
【答案】
A
17.
【答案】
A
18.
【答案】
D
19.
【答案】
C
20.
【答案】
B
二、 填空题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )
21.
【答案】
AE=CF
22.
【答案】
650
23.
【答案】
1255
24.
【答案】
3
25.
【答案】
对角线相等
三、 解答题 (本题共计 5 小题 ,每题 10 分 ,共计50分 )
26.
【答案】
证明:∵ ∠A、∠B、∠C都是直角,
∴ 四边形ABCD是矩形.
27.
【答案】
解:在菱形ABCD中,∠BAO=12∠BAD=12×120?=60?
又在△ABC中,AB=BC,
∴ ∠BCA=∠BAC=60?,
∠ABC=180?-∠BCA-∠BAC=60?,
∴ △ABC为等边三角形
∴ AC=AB=2cm.
在菱形ABCD中,AC⊥BD,
∴ △AOB为直角三角形,
∴ OB2=AB2-AO2,
∴ OB=3,
∴ BD=2BO=23,
∴ S菱形ABCD=12AC?BD=12×2×23=23.
28.
【答案】
(1)证明:∵ 点D,E分别是BC,AB上的中点,
∴ DE?//?AC,AC=2DE,
∵ EF=2DE,
∴ EF?//?AC,EF=AC,
∴ 四边形ACEF是平行四边形,
∴ AF=CE;
(2)解:当∠B=30?时,四边形ACEF是菱形;
理由如下:
∵ ∠ACB=90?,∠B=30?,
∴ ∠BAC=60?,
∵ E是AB的中点,
∴ CE=AE=12AB,
∴ △AEC是等边三角形,
∴ AC=CE,
又∵ 四边形ACEF是平行四边形,
∴ 四边形ACEF是菱形.
29.
【答案】
解:(1)四边形BEMN是菱形,
∵ EF?//?BC,MN?//?AB,
∴ 四边形BEMN是平行四边形,
∵ EF?//?BC,
∴ ∠EMB=∠MBN,
又∵ ∠EBM=∠MBN,
∴ ∠EMB=∠EBM,
∴ EB=EM,
∴ 平行四边形BEMN是菱形;
(2)条件:BA=BC(条件答案不唯一).
∵ BA=BC,BD平分∠ABC,
∴ BD⊥AC,
∵ 四边形BEMN是菱形,
∴ BD⊥EN,
∴ AC?//?EN,
又∵ EF?//?CN,
∴ 四边形EFCN是平行四边形.
30.
【答案】
(1)证明:四边形ABCD是平行四边形∠B=∠D,
∴ AE⊥BC,AF⊥DC,
∠AEB=∠AFD=90?,
∵ BE=DF,
△AEB?△AFD(ASA),
∴ AB=AD,
∴ ∠ABCD 是菱形.
(2)如图,连接BD交AC于点O,
由(1)知四边形ABCD是菱形,
∴ AC⊥BD,AO=OC=12AC,
∵ AC=6,
∴ AO=12×6=3,
∵ AB=5
∴ 在Rt△AOB中,
?BO=AB2-AO2=52-32=4,
∴ BD=2BO=8.
∴ SABCD=12AC?BD=12×6×8=24.
人教版八年级 平行四边形 单元检测题
__ 班级:__________ 姓名:__________ 考号:__________
?
1. 闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB?//?EF?//?DC,BC?//?GH?//?AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )
A.球落在红花丛中和绿花丛中的概率相等
B.球落在紫花丛中和橙花丛中的概率相等
C.球落在红花丛中和蓝花丛中的概率相等
D.球落在蓝花丛中和黄花丛中的概率相等
?
2. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( )
A.2 B.22 C.2 D.1
?
3. 如图,直线,P是直线AB上的动点,当点P的位置变化时,三角形PCD的面积将
A.变小
B.变大
C.不变
D.变大变小要看点P向左还是向右移动
?
4. 如图,在矩形ABCD中,AD=6,对角线AC与BD交于点O,AE⊥BD,垂足为点E,且AE平分∠BAO,则AB的长为( )
A.3 B.4 C.23 D.33
?
5. 如图,AE?//?BD,BE?//?DF,AB?//?CD,下面给出四个结论:
(1)四边形ABDC是平行四边形;(2)BE=DF;(3)SABDC=SBDFE;(4)BD=CE.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
?
6. 下列命题正确的是( )
A.对角线相等的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的平行四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
?
7. 如图,在平行四边形ABCD中,P是AB上一点,E,F分别是BC,AD的中点,连接PE,PC,PD,PF.设平行四边形ABCD的面积为m,则S△PCE+S△PDF=(? ? ? ??)
?
A.14m B.13m C.12m D.35m
?
8. 下列说法中错误的是(? ? ? ? )
A.直角三角形斜边上的中线等于斜边的一半
B.菱形的对角线平分一组对角,并且菱形是轴对称图形
C.矩形的对角线把这个矩形分成4个等腰三角形
D.对角线互相垂直的菱形是正方形
?
9. 如图,?ABCD的对角线AC上有一点P,过P点作HG?//?AB,过P点作MN?//?AD,图中面积相等的平行四边形有几对?(? ? ? ? )
A.1对 B.2对 C.3对 D.4对
?
10. 能判别一个四边形是正方形的条件是( )
A.对角线相等,对边平行且相等
B.一组对边平行,一组对角相等
C.对角线互相垂直平分且相等
D.一组邻边相等,对角线互相平分
?
11. 如图所示,在四边形ABCD中,AD?//?BC,要使四边形ABCD成为平行四边形还需要条件(? ? ? ? )
A.AB=DC B.∠1=∠2 C.AB=AD D.∠D=∠B
?
12. 根据下列条件,能判定平行四边形ABCD是矩形的是(????????)
A.AB=CD,AD=BC B.AB=BC
C.AC=BD D.AB?//?CD,AD?//?BC
?
13. 已知四边形ABCD中,AB?//?CD.则添加下列条件,不能使四边形ABCD成为平行四边形的是( )
A.AB=CD B.∠B=∠D C.AD?//?BC D.AD=BC
?
14. 《几何原本》是古希朋数学家所著的一部数学著作,共13卷,这本著作是现代数学的基础,在西方是仅次于《圣经》而流传最广的书籍.这位古希腊数学家是(????????)
A.利玛窦 B.高斯 C.李善兰 D.欧几里得
?
15. 如图,?ABCD?中.?EF?//?GH?//?BC,MN?//?AB,则图中平行四边形的个数是( )
A.13 B.14 C.15 D.18
?
16. 如图,菱形ABCD的两条对角线AC,BD相交于点O,若AC=6,?BD=8,则菱形ABCD的面积和周长分别为(? ? ? ? )
A.24,?20 B.24,?28 C.40,?20 D.40,?28
?
17. 已知:点D,E分别是△ABC的边AB,AC的中点,如图所示.
求证:DE?//?BC,且DE=12BC.
证明:延长DE到点F,使EF=DE,连接FC,DC,AF,又AE=EC,则四边形ADCF是平行四边形,接着以下是排序错误的证明过程:
①∴ DF∥=BC;
②∴ CF∥=AD.即CF∥=BD;
③∴ 四边形DBCF是平行四边形;
④∴ DE?//?BC,且DE=12BC.
则正确的证明顺序应是:( )
A.②→③→①→④ B.②→①→③→④
C.①→③→④→② D.①→③→②→④
?
18. 如图,已知四边形ABCD和四边形ADEF均为平行四边形,点B,C,F,E在同一直线上,AF交CD于O,若BC=10,AO=FO,则CE的长为( )
A.5 B.10 C.15 D.20
?
19. 如图,在一张△ABC纸片中,∠C=90?,∠B=60?,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
A.1 B.2 C.3 D.4
?
20. 已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=AD时,它是菱形
B.当AC=BD时,它是正方形
C.当∠ABC=90?时,它是矩形
D.当AC⊥BD时,它是菱形
?
21. 如图,E、F是?ABCD对角线AC上不重合的两点.请你添加一个适当的条件,使四边形DEBF是平行四边形.添加的条件可以是________.(只需填写一个正确的结论)
?
22. 如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D,E,测得DE的长度为325米,则A,B两地之间的距离是________米.
?
23. 如图,在矩形ABCD中,AB=3,BC=8,四边形ECGF为菱形,点G在AD上,点B在EF上,若菱形的一条对角线CF=45,则菱形ECGF的另一条对角线EG的长度是__________.
?
24. 若直角三角形斜边长为6cm,则斜边上的中线长为________cm.
?
25. 在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.你添加的条件是________.?(写出一种即可)
?
26. 如图:已知四边形ABCD,∠A、∠B、∠C都是直角.求证:四边形ABCD是矩形.
?
27. 如图:菱形ABCD的边长为2,∠BAD=120?,对角线AC、BD相交于O,求菱形ABCD的面积.
?
28. 如图,在△ABC中,∠ACB=90?,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE,AF.
(1)求证:AF=CE;
(2)当∠B=30?时,试判断四边形ACEF的形状,并说明理由.
?
29. 如图,已知△ABC中,BD平分∠ABC,点M是BD上一点,过M点作EF?//?BC,分别交AB、AC于E、F,作MN?//?AB交BC于N.
(1)试判断四边形BEMN是什么特殊四边形?并证明你的结论.
(2)连接EN,将△ABC再添加一个什么条件时,四边形EFCN是平行四边形?
?
30. 如图6,在平行四边形ABCD中,?AE⊥BC,AF⊥CD?,垂足分别为 E,F,BE=DF.?
(1)求证:平行四边形ABCD是菱形;
(2)若 AB=5,?AC=6,求四边形ABCD的面积.
参考答案与试题解析
一、 选择题 (本题共计 20 小题 ,每题 3 分 ,共计60分 )
1.
【答案】
C
2.
【答案】
B
3.
【答案】
C
4.
【答案】
C
5.
【答案】
B
6.
【答案】
C
7.
【答案】
A
8.
【答案】
D
9.
【答案】
C
10.
【答案】
C
11.
【答案】
D
12.
【答案】
C
13.
【答案】
D
14.
【答案】
D
15.
【答案】
D
16.
【答案】
A
17.
【答案】
A
18.
【答案】
D
19.
【答案】
C
20.
【答案】
B
二、 填空题 (本题共计 5 小题 ,每题 3 分 ,共计15分 )
21.
【答案】
AE=CF
22.
【答案】
650
23.
【答案】
1255
24.
【答案】
3
25.
【答案】
对角线相等
三、 解答题 (本题共计 5 小题 ,每题 10 分 ,共计50分 )
26.
【答案】
证明:∵ ∠A、∠B、∠C都是直角,
∴ 四边形ABCD是矩形.
27.
【答案】
解:在菱形ABCD中,∠BAO=12∠BAD=12×120?=60?
又在△ABC中,AB=BC,
∴ ∠BCA=∠BAC=60?,
∠ABC=180?-∠BCA-∠BAC=60?,
∴ △ABC为等边三角形
∴ AC=AB=2cm.
在菱形ABCD中,AC⊥BD,
∴ △AOB为直角三角形,
∴ OB2=AB2-AO2,
∴ OB=3,
∴ BD=2BO=23,
∴ S菱形ABCD=12AC?BD=12×2×23=23.
28.
【答案】
(1)证明:∵ 点D,E分别是BC,AB上的中点,
∴ DE?//?AC,AC=2DE,
∵ EF=2DE,
∴ EF?//?AC,EF=AC,
∴ 四边形ACEF是平行四边形,
∴ AF=CE;
(2)解:当∠B=30?时,四边形ACEF是菱形;
理由如下:
∵ ∠ACB=90?,∠B=30?,
∴ ∠BAC=60?,
∵ E是AB的中点,
∴ CE=AE=12AB,
∴ △AEC是等边三角形,
∴ AC=CE,
又∵ 四边形ACEF是平行四边形,
∴ 四边形ACEF是菱形.
29.
【答案】
解:(1)四边形BEMN是菱形,
∵ EF?//?BC,MN?//?AB,
∴ 四边形BEMN是平行四边形,
∵ EF?//?BC,
∴ ∠EMB=∠MBN,
又∵ ∠EBM=∠MBN,
∴ ∠EMB=∠EBM,
∴ EB=EM,
∴ 平行四边形BEMN是菱形;
(2)条件:BA=BC(条件答案不唯一).
∵ BA=BC,BD平分∠ABC,
∴ BD⊥AC,
∵ 四边形BEMN是菱形,
∴ BD⊥EN,
∴ AC?//?EN,
又∵ EF?//?CN,
∴ 四边形EFCN是平行四边形.
30.
【答案】
(1)证明:四边形ABCD是平行四边形∠B=∠D,
∴ AE⊥BC,AF⊥DC,
∠AEB=∠AFD=90?,
∵ BE=DF,
△AEB?△AFD(ASA),
∴ AB=AD,
∴ ∠ABCD 是菱形.
(2)如图,连接BD交AC于点O,
由(1)知四边形ABCD是菱形,
∴ AC⊥BD,AO=OC=12AC,
∵ AC=6,
∴ AO=12×6=3,
∵ AB=5
∴ 在Rt△AOB中,
?BO=AB2-AO2=52-32=4,
∴ BD=2BO=8.
∴ SABCD=12AC?BD=12×6×8=24.
