2020-2021学年人教版数学七年级下册 9.2.1 一元一次不等式及其解法 课件(56张)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册 9.2.1 一元一次不等式及其解法 课件(56张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 12:21:30 | ||
图片预览










文档简介
(共56张PPT)
第九章
9.2.1
一元一次不等式及其解法
人教版数学七年级下册
1.掌握一元一次不等式的解法.
2.不等式性质3的运用,由实际问题中的不等式关系列一元一次不等式.
学习目标
1.什么是不等式?
2.什么是不等式的解集?
复习导入
1
知识点
一元一次不等式
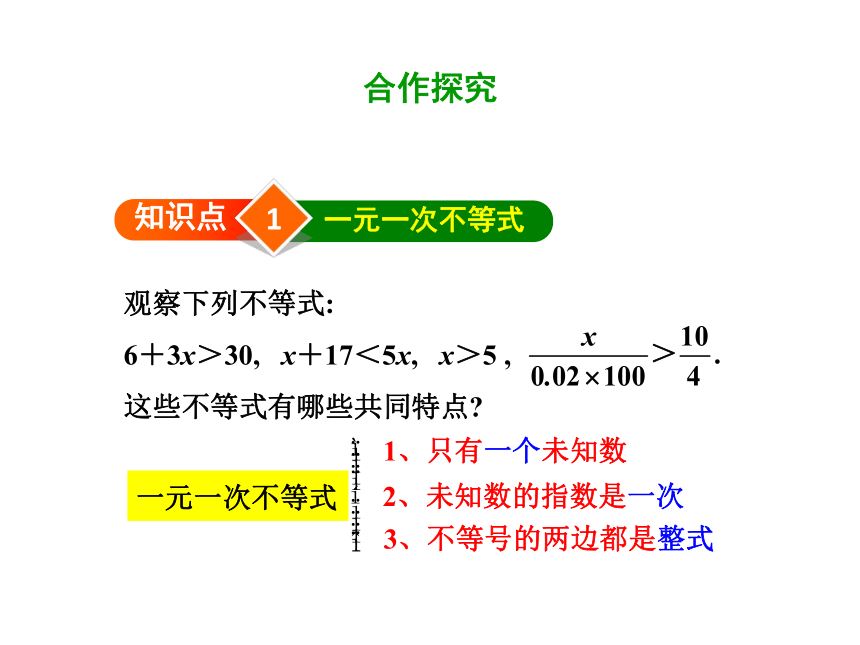
观察下列不等式:
6+3x>30,
x+17<5x,
x>5
,
这些不等式有哪些共同特点?
一元一次不等式
1、只有一个未知数
2、未知数的指数是一次
3、不等号的两边都是整式
合作探究
只含有一个未知数,并且未知数的最高次数1,像这样的不等式,叫做一元一次不等式.
判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
定义
下列式子中是一元一次不等式的有( )
(1)x2+1>2x;(2)
+2>0;
(3)x>y;
(4)
≤1.
A.1个
B.2个
C.3个
D.4个
例1
A
导引:
(1)中未知数的最高次数是2,故不是一元一次不
等式;(2)中左边不是整式,故不是一元一次不
等式;(3)中有两个未知数,故不是一元一次不
等式;(4)是一元一次不等式.
判断一个不等式是否为一元一次不等式的步骤:
先对所给不等式进行化简整理,再看是否满足:
(1)不等式的左、右两边都是整式;
(2)不等式中只含有一个未知数;
(3)未知数的次数是1且系数不为0.
当这三个条件同时满足时,才能判定该不等式是一
元一次不等式.
新知小结
下列不等式中,是一元一次不等式的是( )
B.a2+b2>0
C.
>1
D.x<y
1
A
巩固新知
2
知识点
解一元一次不等式
解一元一次不等式与解一元一次方程的步骤类似.
解
一元一次不等式的一般步骤和根据如下:
步骤
根据
1
去分母
不等式的基本性质
3
2
去括号
单项式乘以多项式法则
3
移项
不等式的基本性质
3
4
合并同类项,得ax>b,或ax(a≠0)
合并同类项法则
5
两边同除以a(或乘
)
不等式的基本性质
3
合作探究
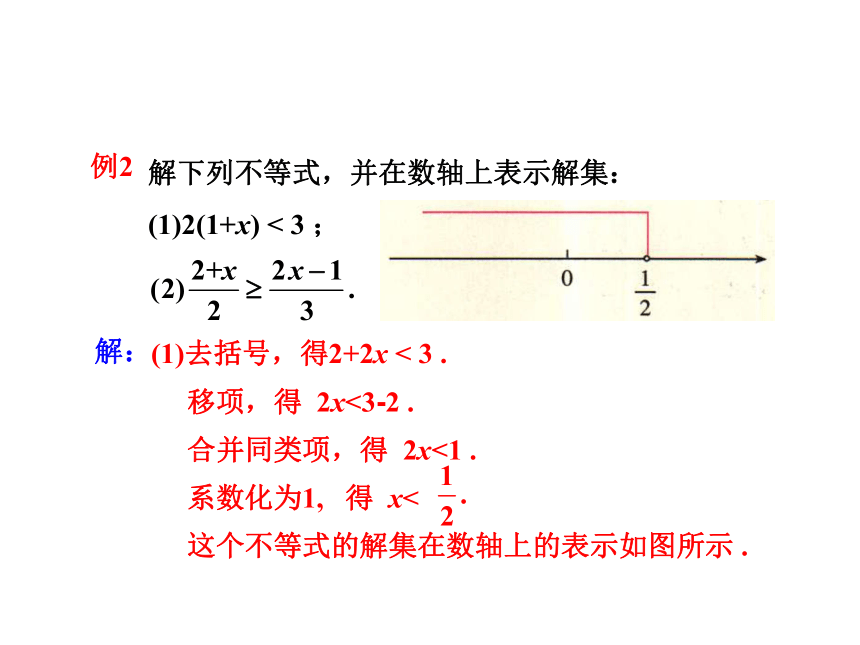
解下列不等式,并在数轴上表示解集:
(1)2(1+x)
<
3
;
例2
解:
(1)去括号,得2+2x
<
3
.
移项,得
2x<3-2
.
合并同类项,得
2x<1
.
系数化为1,
得
x<
这个不等式的解集在数轴上的表示如图所示
.
(2)
去分母,得3(2+x)≥2(2x-1).
去括号,得
6+3x
≥4
x-2
.
移项,得
3x-
4x
≤
-2-6
.
合并同类项,得
-x
≥
-8
.
系数化为1,得x
≤
8
.
这个不等式的解集在数轴上的表示如图所示
.
一元一次不等式的解法与一元一次方程的解法
类似,其根据是不等式的基本性质,其步骤是:去
分母、去括号、移项、合并同类项、将未知数的系
数化为
1.
新知小结
1
解下列不等式,并在数轴上表示解集:
(1)
5x+15>4x-1;
(2)
2(x+5)≤3(x-5);
巩固新知
(1)移项,得5x-4x>-1-15,
合并同类项,得x>-16.
这个不等式的解集在数轴上的表示略.
(2)去括号,得2x+10≤3x-15,
移项,得2x-3x≤-15-10,
合并同类项,得-x≤-25,
系数化为1,得x≥25.
这个不等式的解集在数轴上的表示略.
解:
(3)去分母,得3(x-1)<7(2x+5),
去括号,得3x-3<14x+35,
移项,得3x-14x<35+3,
合并同类项,得-11x<38,
系数化为1,得x>-
这个不等式的解集在数轴上的表示略.
(4)去分母,得2(x+1)≥3(2x-5)+12,
去括号,得2x+2≥6x-15+12,
移项,合并同类项,得-4x≥-5,
系数化为1,得x
≤
这个不等式的解集在数轴上的表示略.
2
当x或y满足什么条件时,下列关系成立?
2(x+1)大于或等于1;
4x与7的和不小于6;
(3)
y与1的差不大于2y与3的差;
(4)
3y与7的和的四分之一小于-2.
(1)由题意,得2(x+1)≥1,2x+2≥1,2x≥-1,
x≥-
.
所以,当x≥-
时,2(x+1)大于或等于1.
(2)由题意,得4x+7≥6,4x≥-1,x≥-
.
所以,当x≥-
时,4x与7的和不小于6.
解:
(3)由题意,得y-1≤2y-3,解得y≥2.
所以,当y≥2时,
y与1的差不大于2y与3的差.
(4)由题意,得
(3y+7)<-2,解得y<-5.
所以,当y<-5时,
3y与7的和的四分之一小于-2.
3
解不等式
≥x-1,下列去分母正
确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
D
4
解不等式
的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.①
B.②
C.③
D.④
D
5
【中考·安徽】不等式4-2x>0的解集在数轴上表示为( )
D
6 (中考·贵州)不等式3x+2<2x+3的解集在数轴上表示正确的是( )
D
7
【中考·丽水】若关于x的一元一次方程x-m+2=0的解是负数,则m的取值范围是( )
A.m≥2
B.m>2
C.m<2
D.m≤2
C
8
若不等式
的解集是x<
则a的取值情况是( )
A.a>5
B.a=5
C.a>-5
D.a=-5
B
3
知识点
一元一次不等式的特殊解
求不等式3(x+1)≥5x-9的非负整数解.
例3
导引:
求不等式的非负整数解,即在原不等式的解集
中找出它所包含的“非负整数”特殊解;因此
先需求出原不等式的解集.
∵解不等式3(x+1)≥5x-9得x≤6.
∴不等式3(x+1)≥5x-9的非负整数解为
0,1,2,3,4,5,6.
解:
合作探究
正确理解关键词语的含义是准确解题的关键,
“非负整数解”即0和正整数解.
新知小结
1 (中考·南通)关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )
A.-3<b<-2
B.-3<b≤-2
C.-3≤b≤-2
D.-3≤b<-2
2 当自然数k=__________时,关于x的方程
x-3k=5(x-k)+6的解是负数.
D
0,1,2
巩固新知
一元一次不等式的判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
1
知识小结
归纳新知
2.
解一元一次不等式的一般步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)未知数的系数化为1.
下列不等式中,是一元一次不等式的是( )
A.2x2-5>0
B.
+x<5
C.-5y+8>0
D.2x+3>2(1+x)
易错点:判断一元一次不等式时忽视隐含条件
2
易错小结
C
此题学生常常不化简直接进行判断而错选D.
1.左右两边都是整式,只含有________个未知数,并且未知数的最高次数是1的不等式,叫做一元一次不等式.
一
课后练习
【点拨】依题意得m2=1且m+1≠0,解得m=1.
B
3.下列不等式:①
-2<0;②
3x-5>0;③
x2-x>1;
④
x>1;⑤
-2>0;⑥
x+2>y+1中,一元一次不等式有( )
A.2个
B.3个
C.4个
D.5个
A
4.解一元一次不等式,要依据____________________,将不等式逐步化为__________________________的形式.
一般步骤为:(1)__________;(2)去括号;(3)________;
(4)合并同类项;(5)系数化为________.
不等式的性质
x<a(或x≤a)或x>a(或x≥a)
去分母
移项
1
5.下面解不等式>的过程中,有错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项,得5x-6x>-10-3;
④合并同类项,得-x>-13;⑤系数化为1,得x>13.
A.①
B.②
C.③
D.⑤
D
【点拨】不等式的两边都乘(或除以)同一个负数,不等号的方向改变,故⑤不正确.
A
6.(2019·武威)不等式2x+9≥3(x+2)的解集是( )
A.x≤3
B.x≤-3
C.x≥3
D.x≥-3
7.(2020·嘉兴)不等式3(1-x)>2-4x的解集在数轴上表示正确的是( )
A
【答案】C
9.一元一次不等式的特殊解问题分两步解答:
一是求出一元一次不等式的____________________;
二是根据问题条件,在所得解集内确定满足条件的解.
解集
C
11.(中考·大庆)若实数3是不等式2x-a-2<0的一个解,则a可取的最小正整数为( )
A.2
B.3
C.4
D.5
D
12.(2020·天水)若关于x的不等式3x+a≤2只有2个正整数解,则a的取值范围为( )
A.-7<a<-4
B.-7≤a≤-4
C.-7≤a<-4
D.-7<a≤-4
D
解:去括号,得4x-2>3x-1,
移项,得4x-3x>2-1,
合并同类项,得x>1.
(2)解题回顾:本题“去分母”这一步的变形依据是________(填“A”或“B”).
A.不等式两边都乘(或除以)同一个正数,不等号的方向不变;
B.不等式两边都乘(或除以)同一个负数,不等号的方向改变.
A
(2)若再添一个负整数m,且-9,5与m这三个数的平均数仍小于m,求m的值.
16.关于x的不等式-k-x+6>0的正整数解是1,2,3,4,求k的取值范围.
解:解不等式-k-x+6>0,得x<6-k.
根据题意,得4<6-k≤5,
解得1≤k<2.
17.(中考·南京)如图,在数轴上,点A,B分别表示数1,-2x+3.
(1)求x的取值范围;
解:由题意得-2x+3>1,解得x<1.
(2)数轴上表示数-x+2的点应落在______.
A.点A的左边
B.线段AB上
C.点B的右边
B
18.(2020·张家界)阅读下面的材料:
对于实数a,b,我们定义符号min{a,b}的意义为:当a<b时,min{a,b}=a;当a≥b时,min{a,b}=b,如:min{4,-2}=-2,min{5,5}=5.
根据上面的材料回答下列问题:
(1)min{-1,3}=________;
-1
再见
第九章
9.2.1
一元一次不等式及其解法
人教版数学七年级下册
1.掌握一元一次不等式的解法.
2.不等式性质3的运用,由实际问题中的不等式关系列一元一次不等式.
学习目标
1.什么是不等式?
2.什么是不等式的解集?
复习导入
1
知识点
一元一次不等式
观察下列不等式:
6+3x>30,
x+17<5x,
x>5
,
这些不等式有哪些共同特点?
一元一次不等式
1、只有一个未知数
2、未知数的指数是一次
3、不等号的两边都是整式
合作探究
只含有一个未知数,并且未知数的最高次数1,像这样的不等式,叫做一元一次不等式.
判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
定义
下列式子中是一元一次不等式的有( )
(1)x2+1>2x;(2)
+2>0;
(3)x>y;
(4)
≤1.
A.1个
B.2个
C.3个
D.4个
例1
A
导引:
(1)中未知数的最高次数是2,故不是一元一次不
等式;(2)中左边不是整式,故不是一元一次不
等式;(3)中有两个未知数,故不是一元一次不
等式;(4)是一元一次不等式.
判断一个不等式是否为一元一次不等式的步骤:
先对所给不等式进行化简整理,再看是否满足:
(1)不等式的左、右两边都是整式;
(2)不等式中只含有一个未知数;
(3)未知数的次数是1且系数不为0.
当这三个条件同时满足时,才能判定该不等式是一
元一次不等式.
新知小结
下列不等式中,是一元一次不等式的是( )
B.a2+b2>0
C.
>1
D.x<y
1
A
巩固新知
2
知识点
解一元一次不等式
解一元一次不等式与解一元一次方程的步骤类似.
解
一元一次不等式的一般步骤和根据如下:
步骤
根据
1
去分母
不等式的基本性质
3
2
去括号
单项式乘以多项式法则
3
移项
不等式的基本性质
3
4
合并同类项,得ax>b,或ax
合并同类项法则
5
两边同除以a(或乘
)
不等式的基本性质
3
合作探究
解下列不等式,并在数轴上表示解集:
(1)2(1+x)
<
3
;
例2
解:
(1)去括号,得2+2x
<
3
.
移项,得
2x<3-2
.
合并同类项,得
2x<1
.
系数化为1,
得
x<
这个不等式的解集在数轴上的表示如图所示
.
(2)
去分母,得3(2+x)≥2(2x-1).
去括号,得
6+3x
≥4
x-2
.
移项,得
3x-
4x
≤
-2-6
.
合并同类项,得
-x
≥
-8
.
系数化为1,得x
≤
8
.
这个不等式的解集在数轴上的表示如图所示
.
一元一次不等式的解法与一元一次方程的解法
类似,其根据是不等式的基本性质,其步骤是:去
分母、去括号、移项、合并同类项、将未知数的系
数化为
1.
新知小结
1
解下列不等式,并在数轴上表示解集:
(1)
5x+15>4x-1;
(2)
2(x+5)≤3(x-5);
巩固新知
(1)移项,得5x-4x>-1-15,
合并同类项,得x>-16.
这个不等式的解集在数轴上的表示略.
(2)去括号,得2x+10≤3x-15,
移项,得2x-3x≤-15-10,
合并同类项,得-x≤-25,
系数化为1,得x≥25.
这个不等式的解集在数轴上的表示略.
解:
(3)去分母,得3(x-1)<7(2x+5),
去括号,得3x-3<14x+35,
移项,得3x-14x<35+3,
合并同类项,得-11x<38,
系数化为1,得x>-
这个不等式的解集在数轴上的表示略.
(4)去分母,得2(x+1)≥3(2x-5)+12,
去括号,得2x+2≥6x-15+12,
移项,合并同类项,得-4x≥-5,
系数化为1,得x
≤
这个不等式的解集在数轴上的表示略.
2
当x或y满足什么条件时,下列关系成立?
2(x+1)大于或等于1;
4x与7的和不小于6;
(3)
y与1的差不大于2y与3的差;
(4)
3y与7的和的四分之一小于-2.
(1)由题意,得2(x+1)≥1,2x+2≥1,2x≥-1,
x≥-
.
所以,当x≥-
时,2(x+1)大于或等于1.
(2)由题意,得4x+7≥6,4x≥-1,x≥-
.
所以,当x≥-
时,4x与7的和不小于6.
解:
(3)由题意,得y-1≤2y-3,解得y≥2.
所以,当y≥2时,
y与1的差不大于2y与3的差.
(4)由题意,得
(3y+7)<-2,解得y<-5.
所以,当y<-5时,
3y与7的和的四分之一小于-2.
3
解不等式
≥x-1,下列去分母正
确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
D
4
解不等式
的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.①
B.②
C.③
D.④
D
5
【中考·安徽】不等式4-2x>0的解集在数轴上表示为( )
D
6 (中考·贵州)不等式3x+2<2x+3的解集在数轴上表示正确的是( )
D
7
【中考·丽水】若关于x的一元一次方程x-m+2=0的解是负数,则m的取值范围是( )
A.m≥2
B.m>2
C.m<2
D.m≤2
C
8
若不等式
的解集是x<
则a的取值情况是( )
A.a>5
B.a=5
C.a>-5
D.a=-5
B
3
知识点
一元一次不等式的特殊解
求不等式3(x+1)≥5x-9的非负整数解.
例3
导引:
求不等式的非负整数解,即在原不等式的解集
中找出它所包含的“非负整数”特殊解;因此
先需求出原不等式的解集.
∵解不等式3(x+1)≥5x-9得x≤6.
∴不等式3(x+1)≥5x-9的非负整数解为
0,1,2,3,4,5,6.
解:
合作探究
正确理解关键词语的含义是准确解题的关键,
“非负整数解”即0和正整数解.
新知小结
1 (中考·南通)关于x的不等式x-b>0恰有两个负整数解,则b的取值范围是( )
A.-3<b<-2
B.-3<b≤-2
C.-3≤b≤-2
D.-3≤b<-2
2 当自然数k=__________时,关于x的方程
x-3k=5(x-k)+6的解是负数.
D
0,1,2
巩固新知
一元一次不等式的判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
1
知识小结
归纳新知
2.
解一元一次不等式的一般步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)未知数的系数化为1.
下列不等式中,是一元一次不等式的是( )
A.2x2-5>0
B.
+x<5
C.-5y+8>0
D.2x+3>2(1+x)
易错点:判断一元一次不等式时忽视隐含条件
2
易错小结
C
此题学生常常不化简直接进行判断而错选D.
1.左右两边都是整式,只含有________个未知数,并且未知数的最高次数是1的不等式,叫做一元一次不等式.
一
课后练习
【点拨】依题意得m2=1且m+1≠0,解得m=1.
B
3.下列不等式:①
-2<0;②
3x-5>0;③
x2-x>1;
④
x>1;⑤
-2>0;⑥
x+2>y+1中,一元一次不等式有( )
A.2个
B.3个
C.4个
D.5个
A
4.解一元一次不等式,要依据____________________,将不等式逐步化为__________________________的形式.
一般步骤为:(1)__________;(2)去括号;(3)________;
(4)合并同类项;(5)系数化为________.
不等式的性质
x<a(或x≤a)或x>a(或x≥a)
去分母
移项
1
5.下面解不等式>的过程中,有错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项,得5x-6x>-10-3;
④合并同类项,得-x>-13;⑤系数化为1,得x>13.
A.①
B.②
C.③
D.⑤
D
【点拨】不等式的两边都乘(或除以)同一个负数,不等号的方向改变,故⑤不正确.
A
6.(2019·武威)不等式2x+9≥3(x+2)的解集是( )
A.x≤3
B.x≤-3
C.x≥3
D.x≥-3
7.(2020·嘉兴)不等式3(1-x)>2-4x的解集在数轴上表示正确的是( )
A
【答案】C
9.一元一次不等式的特殊解问题分两步解答:
一是求出一元一次不等式的____________________;
二是根据问题条件,在所得解集内确定满足条件的解.
解集
C
11.(中考·大庆)若实数3是不等式2x-a-2<0的一个解,则a可取的最小正整数为( )
A.2
B.3
C.4
D.5
D
12.(2020·天水)若关于x的不等式3x+a≤2只有2个正整数解,则a的取值范围为( )
A.-7<a<-4
B.-7≤a≤-4
C.-7≤a<-4
D.-7<a≤-4
D
解:去括号,得4x-2>3x-1,
移项,得4x-3x>2-1,
合并同类项,得x>1.
(2)解题回顾:本题“去分母”这一步的变形依据是________(填“A”或“B”).
A.不等式两边都乘(或除以)同一个正数,不等号的方向不变;
B.不等式两边都乘(或除以)同一个负数,不等号的方向改变.
A
(2)若再添一个负整数m,且-9,5与m这三个数的平均数仍小于m,求m的值.
16.关于x的不等式-k-x+6>0的正整数解是1,2,3,4,求k的取值范围.
解:解不等式-k-x+6>0,得x<6-k.
根据题意,得4<6-k≤5,
解得1≤k<2.
17.(中考·南京)如图,在数轴上,点A,B分别表示数1,-2x+3.
(1)求x的取值范围;
解:由题意得-2x+3>1,解得x<1.
(2)数轴上表示数-x+2的点应落在______.
A.点A的左边
B.线段AB上
C.点B的右边
B
18.(2020·张家界)阅读下面的材料:
对于实数a,b,我们定义符号min{a,b}的意义为:当a<b时,min{a,b}=a;当a≥b时,min{a,b}=b,如:min{4,-2}=-2,min{5,5}=5.
根据上面的材料回答下列问题:
(1)min{-1,3}=________;
-1
再见
