2020-2021学年人教版数学八年级下册 18.2.2 菱形的判定 课件 (54张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册 18.2.2 菱形的判定 课件 (54张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 12:28:05 | ||
图片预览






文档简介
第十八章
18.2.4 菱形的判定
人教版数学八年级下册
A
B
C
D
O
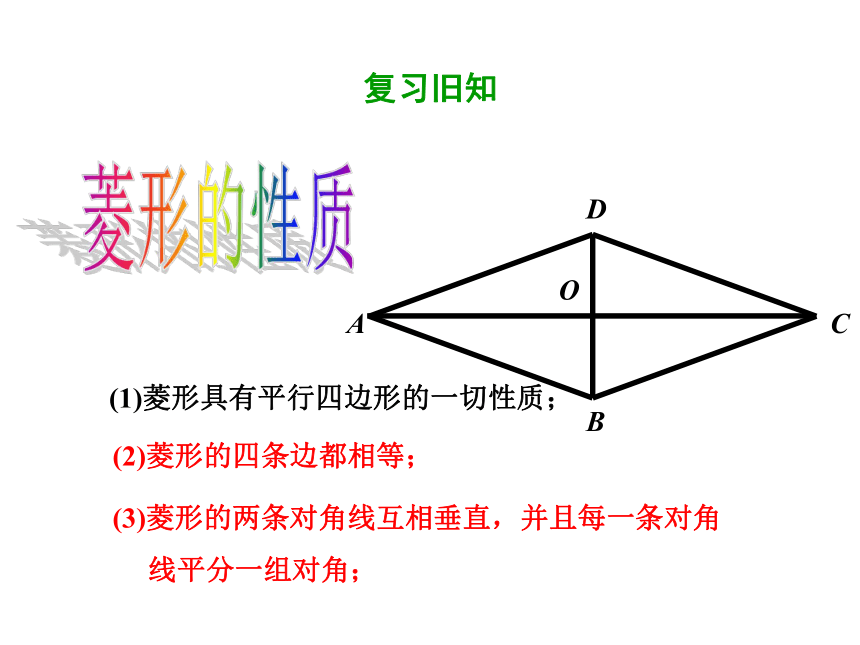
(1)菱形具有平行四边形的一切性质;
(2)菱形的四条边都相等;
(3)菱形的两条对角线互相垂直,并且每一条对角
线平分一组对角;
菱形的性质
复习旧知
同学们,我们已经知道,有一组邻边相等的平行四边形是菱形.这是菱形的定义,我们可以根据定义来判定一个四边形是菱形.除此之外,还能找到其他的判定方法吗?
菱形的判定
导入新知
学习目标
1.掌握菱形的判定方法.
2.探究菱形的判定条件并合理利用它进行论证和计算.
1
知识点
由对角线的位置关系判定菱形
同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?
根据定义得:一组邻边相等的平行四边形是菱形.
合作探究
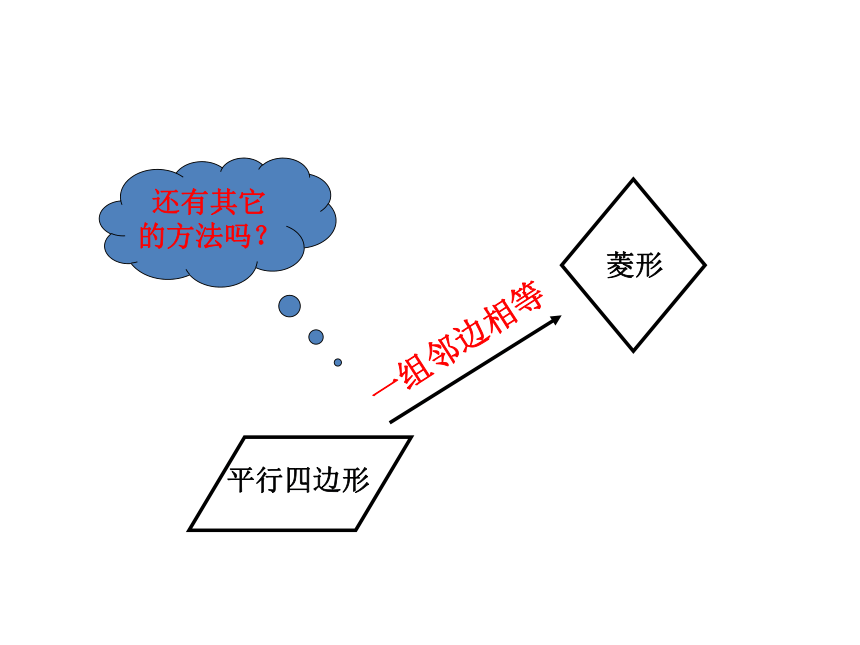
平行四边形
菱形
一组邻边相等
还有其它的方法吗?
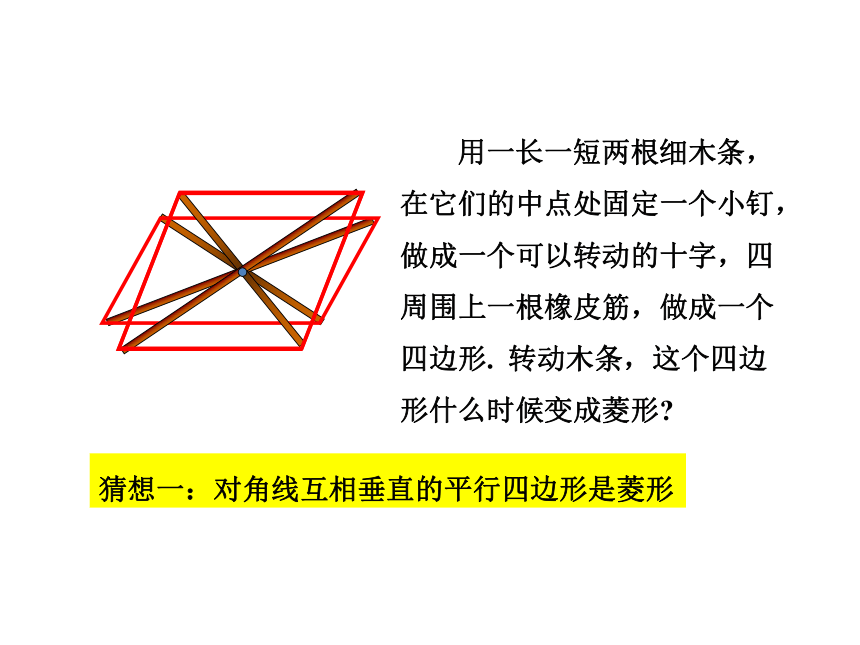
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形. 转动木条,这个四边形什么时候变成菱形?
猜想一:对角线互相垂直的平行四边形是菱形
证明:
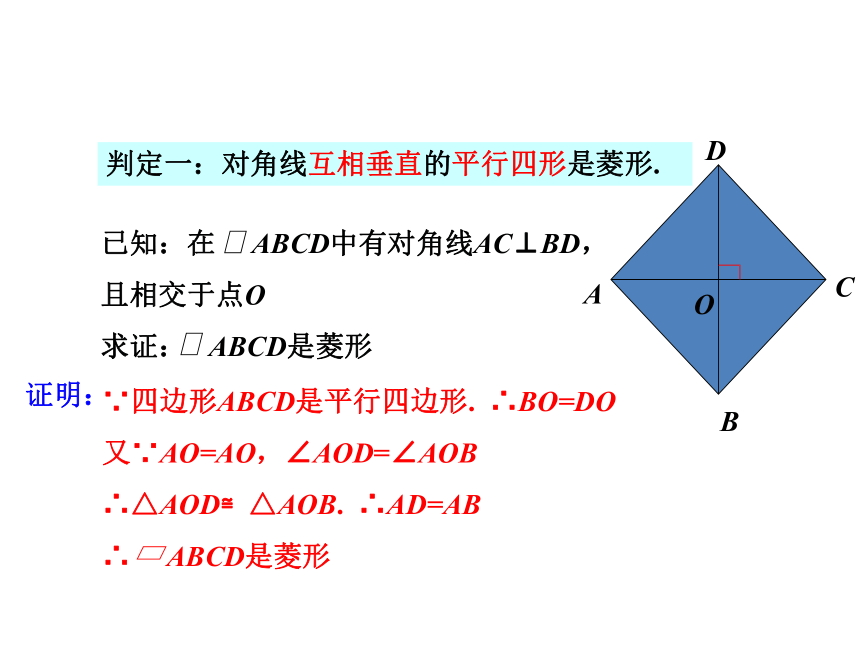
判定一:对角线互相垂直的平行四形是菱形.
D
C
B
A
已知:在 ABCD中有对角线AC⊥BD,
且相交于点O
求证: ABCD是菱形
∵四边形ABCD是平行四边形. ∴BO=DO
又∵AO=AO,∠AOD=∠AOB
∴△AOD≌△AOB. ∴AD=AB
∴ ABCD是菱形
O
对角线互相垂直的平行四边形是菱形.
提示:此方法包括两个条件——
(1)是一个平行四边形;
(2)两条对角线互相垂直.
对角线互相垂直且平分的四边形是菱形.
新知小结
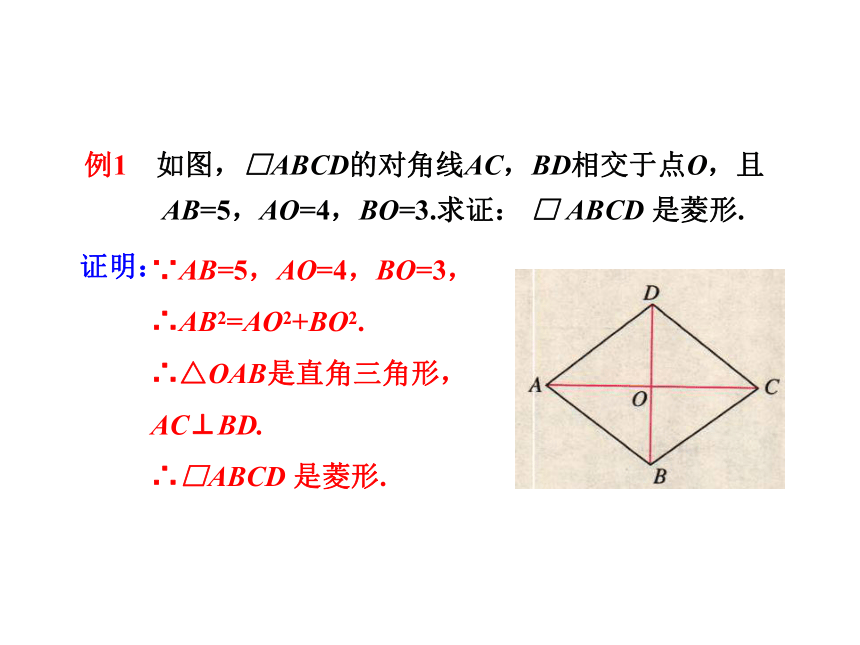
例1 如图,□ABCD的对角线AC,BD相交于点O,且
AB=5,AO=4,BO=3.求证: □ ABCD 是菱形.
∵AB=5,AO=4,BO=3,
∴AB2=AO2+BO2.
∴△OAB是直角三角形,
AC⊥BD.
∴□ABCD 是菱形.
证明:
证明一个四边形是菱形的方法:
若已知要证的四边形的对角线互相垂直,则要
考虑证明这个四边形是平行四边形.
新知小结
1
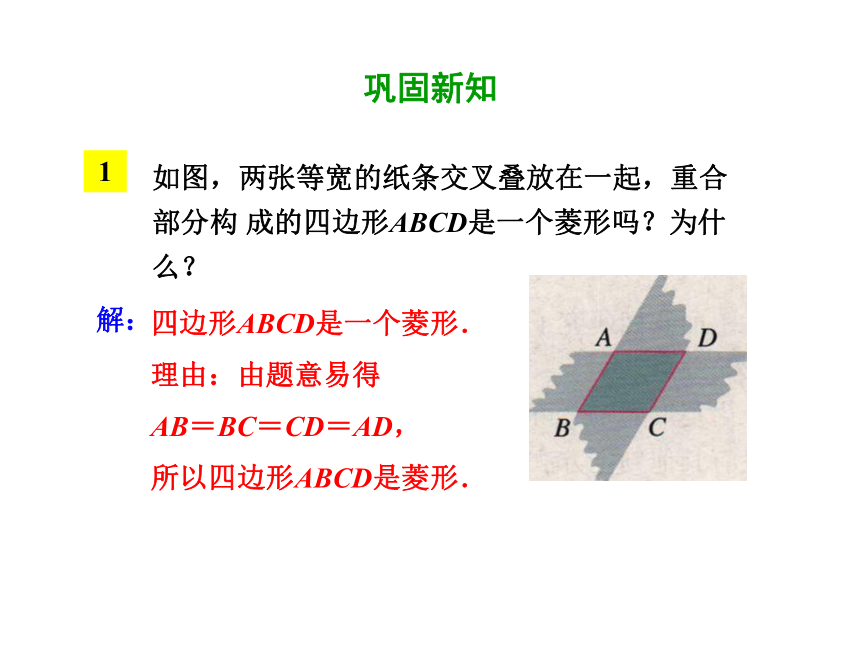
如图,两张等宽的纸条交叉叠放在一起,重合部分构 成的四边形ABCD是一个菱形吗?为什么?
四边形ABCD是一个菱形.
理由:由题意易得
AB=BC=CD=AD,
所以四边形ABCD是菱形.
解:
巩固新知
2
【2016·海南】如图,四边形 ABCD 是轴对称图形,且直线 AC 是对称轴,BD与AC交于点O,AB∥CD,则下列结论:
①AC⊥BD;②AD∥ BC;
③四边形 ABCD 是菱形;
④△ABD≌△CDB.
其中正确的是____________(只填写序号).
①②③④
3
【2017·泰安】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,其中正确结论的个数为( )
A.1 B.2
C.3 D.4
D
2
知识点
由边的数量关系判定菱形
我们知道,菱形的四条边相等. 反过来,四条边
相等的四边形是菱形吗?
思考
合作探究
例2 如图,在四边形ABCD中,AD∥BC,AB=CD,
点E,F,G,H分别是AD,BD,BC,AC的中
点.试说明:四边形EFGH是菱形.
由于点E,F,G,H分别是AD,BD,
BC,AC的中点,可知EH,HG,
GF,FE分别是△ACD,△ABC,△BCD,△ABD
的中位线,又∵AB=CD,∴EH=HG=GF=FE,
根据“四条边相等的四边形是菱形”可得四边形
EFGH是菱形.
导引:
∵点E,H分别为AD,AC的中点,
∴EH为△ACD的中位线,∴EH= CD.
同理可证:EF= AB,FG= CD,HG= AB.
∵AB=CD,
∴EH=EF=FG=HG,
∴四边形EFGH是菱形.
解:
有较多线段相等的条件时,我们可考虑通过证明
四条边相等来证明这个四边形是菱形.注意:本例也
可以通过先证四边形EFGH是平行四边形,再证一组
邻边相等,只不过步骤复杂一点,读者不妨试一试.
新知小结
要证明一个四边形是菱形,
一般先证明它是平行四边
形,再证明它的一组邻边
相等或对角线互相垂直.
例3 如图,在△ABC中,∠ACB=90°,AD平分∠BAC
交BC于点D,CH⊥AB于点H,交AD于点F,DE⊥
AB于点E,那么四边形CDEF是菱形吗?说说你的
理由.
导引:
四边形CDEF是菱形.理由如下:
∵CH⊥AB,DE⊥AB,∴CF∥DE,∠4+∠5=90°.
∵∠ACB=90°,∴∠2+∠3=90°,DC⊥AC.
又∵AD平分∠BAC,DE⊥AB,
∴∠3=∠4,DC=DE,∴∠2=∠5.
又∵∠1=∠5,∴∠1=∠2.
∴CF=CD,∴CF=DE,即CF DE.
∴四边形CDEF是平行四边形.
又∵DC=DE,∴四边形CDEF是菱形.
∥
=
解:
判定菱形的方法:
①若用对角线进行判定:先证明四边形是平行四边形,
再证明对角线互相垂直,或直接证明四边形的对角
线互相垂直平分;
②若用边进行判定:先证明四边形是平行四边形,再
证明一组邻边相等,或直接证明四边形的四条边都
相等.
新知小结
一个平行四边形的一条边长是9,两条对角线的长分别是12和 ,这是一个特殊的平行四边形吗?为什 么?求出它的面积.
1
这是一个特殊的平行四边形,是菱形.
如图,在平行四边形ABCD中,
AB=9,BD=12,AC=
所以OB=OD=6,
OA=OC=
解:
巩固新知
因为62+( )2=92,即OB2+OA2=AB2,
所以△AOB是直角三角形,
所以AO⊥BO,即AC⊥BD,
所以平行四边形ABCD是菱形.
S菱形ABCD= AC·BD= ×6 ×12=36 .
2
如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A.BA=BC
B.AC,BD互相平分
C.AC=BD
D.AB∥CD
B
3
【2017·河南】如图,在?ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定?ABCD是菱形的只有( )
A.AC⊥BD
B.AB=BC
C.AC=BD
D.∠1=∠2
C
4
【2016·雅安】如图,四边形ABCD的四边相等,且面积为120 cm2,对角线AC =24 cm,则四边形ABCD的周长为 ( )
A.52 cm
B.40 cm
C.39 cm
D.26 cm
A
5
如图,在△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.如果AE=4 cm,那么四边形AEDF的周长为( )
A.12 cm
B.16 cm
C.20 cm
D.22 cm
B
6
如图,分别以Rt△ABC的斜边AB和直角边AC为边向△ABC外作等边三角形ABD和等边三角形ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠BAC=30°.给出以下结论:
①EF⊥AC;
②四边形ADFE为菱形;
③AD=4AG; ④FH= BD.
其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.②③④
C
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
菱形的判定方法:
归纳新知
互相垂直
四边形
课后练习
C
D
【答案】C
一组邻边相等
四边形
C
A
B
C
【答案】D
再 见
18.2.4 菱形的判定
人教版数学八年级下册
A
B
C
D
O
(1)菱形具有平行四边形的一切性质;
(2)菱形的四条边都相等;
(3)菱形的两条对角线互相垂直,并且每一条对角
线平分一组对角;
菱形的性质
复习旧知
同学们,我们已经知道,有一组邻边相等的平行四边形是菱形.这是菱形的定义,我们可以根据定义来判定一个四边形是菱形.除此之外,还能找到其他的判定方法吗?
菱形的判定
导入新知
学习目标
1.掌握菱形的判定方法.
2.探究菱形的判定条件并合理利用它进行论证和计算.
1
知识点
由对角线的位置关系判定菱形
同学们想一想,我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么?那么类比着它们,菱形的第一种判定方法是什么?
根据定义得:一组邻边相等的平行四边形是菱形.
合作探究
平行四边形
菱形
一组邻边相等
还有其它的方法吗?
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形. 转动木条,这个四边形什么时候变成菱形?
猜想一:对角线互相垂直的平行四边形是菱形
证明:
判定一:对角线互相垂直的平行四形是菱形.
D
C
B
A
已知:在 ABCD中有对角线AC⊥BD,
且相交于点O
求证: ABCD是菱形
∵四边形ABCD是平行四边形. ∴BO=DO
又∵AO=AO,∠AOD=∠AOB
∴△AOD≌△AOB. ∴AD=AB
∴ ABCD是菱形
O
对角线互相垂直的平行四边形是菱形.
提示:此方法包括两个条件——
(1)是一个平行四边形;
(2)两条对角线互相垂直.
对角线互相垂直且平分的四边形是菱形.
新知小结
例1 如图,□ABCD的对角线AC,BD相交于点O,且
AB=5,AO=4,BO=3.求证: □ ABCD 是菱形.
∵AB=5,AO=4,BO=3,
∴AB2=AO2+BO2.
∴△OAB是直角三角形,
AC⊥BD.
∴□ABCD 是菱形.
证明:
证明一个四边形是菱形的方法:
若已知要证的四边形的对角线互相垂直,则要
考虑证明这个四边形是平行四边形.
新知小结
1
如图,两张等宽的纸条交叉叠放在一起,重合部分构 成的四边形ABCD是一个菱形吗?为什么?
四边形ABCD是一个菱形.
理由:由题意易得
AB=BC=CD=AD,
所以四边形ABCD是菱形.
解:
巩固新知
2
【2016·海南】如图,四边形 ABCD 是轴对称图形,且直线 AC 是对称轴,BD与AC交于点O,AB∥CD,则下列结论:
①AC⊥BD;②AD∥ BC;
③四边形 ABCD 是菱形;
④△ABD≌△CDB.
其中正确的是____________(只填写序号).
①②③④
3
【2017·泰安】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,其中正确结论的个数为( )
A.1 B.2
C.3 D.4
D
2
知识点
由边的数量关系判定菱形
我们知道,菱形的四条边相等. 反过来,四条边
相等的四边形是菱形吗?
思考
合作探究
例2 如图,在四边形ABCD中,AD∥BC,AB=CD,
点E,F,G,H分别是AD,BD,BC,AC的中
点.试说明:四边形EFGH是菱形.
由于点E,F,G,H分别是AD,BD,
BC,AC的中点,可知EH,HG,
GF,FE分别是△ACD,△ABC,△BCD,△ABD
的中位线,又∵AB=CD,∴EH=HG=GF=FE,
根据“四条边相等的四边形是菱形”可得四边形
EFGH是菱形.
导引:
∵点E,H分别为AD,AC的中点,
∴EH为△ACD的中位线,∴EH= CD.
同理可证:EF= AB,FG= CD,HG= AB.
∵AB=CD,
∴EH=EF=FG=HG,
∴四边形EFGH是菱形.
解:
有较多线段相等的条件时,我们可考虑通过证明
四条边相等来证明这个四边形是菱形.注意:本例也
可以通过先证四边形EFGH是平行四边形,再证一组
邻边相等,只不过步骤复杂一点,读者不妨试一试.
新知小结
要证明一个四边形是菱形,
一般先证明它是平行四边
形,再证明它的一组邻边
相等或对角线互相垂直.
例3 如图,在△ABC中,∠ACB=90°,AD平分∠BAC
交BC于点D,CH⊥AB于点H,交AD于点F,DE⊥
AB于点E,那么四边形CDEF是菱形吗?说说你的
理由.
导引:
四边形CDEF是菱形.理由如下:
∵CH⊥AB,DE⊥AB,∴CF∥DE,∠4+∠5=90°.
∵∠ACB=90°,∴∠2+∠3=90°,DC⊥AC.
又∵AD平分∠BAC,DE⊥AB,
∴∠3=∠4,DC=DE,∴∠2=∠5.
又∵∠1=∠5,∴∠1=∠2.
∴CF=CD,∴CF=DE,即CF DE.
∴四边形CDEF是平行四边形.
又∵DC=DE,∴四边形CDEF是菱形.
∥
=
解:
判定菱形的方法:
①若用对角线进行判定:先证明四边形是平行四边形,
再证明对角线互相垂直,或直接证明四边形的对角
线互相垂直平分;
②若用边进行判定:先证明四边形是平行四边形,再
证明一组邻边相等,或直接证明四边形的四条边都
相等.
新知小结
一个平行四边形的一条边长是9,两条对角线的长分别是12和 ,这是一个特殊的平行四边形吗?为什 么?求出它的面积.
1
这是一个特殊的平行四边形,是菱形.
如图,在平行四边形ABCD中,
AB=9,BD=12,AC=
所以OB=OD=6,
OA=OC=
解:
巩固新知
因为62+( )2=92,即OB2+OA2=AB2,
所以△AOB是直角三角形,
所以AO⊥BO,即AC⊥BD,
所以平行四边形ABCD是菱形.
S菱形ABCD= AC·BD= ×6 ×12=36 .
2
如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
A.BA=BC
B.AC,BD互相平分
C.AC=BD
D.AB∥CD
B
3
【2017·河南】如图,在?ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定?ABCD是菱形的只有( )
A.AC⊥BD
B.AB=BC
C.AC=BD
D.∠1=∠2
C
4
【2016·雅安】如图,四边形ABCD的四边相等,且面积为120 cm2,对角线AC =24 cm,则四边形ABCD的周长为 ( )
A.52 cm
B.40 cm
C.39 cm
D.26 cm
A
5
如图,在△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.如果AE=4 cm,那么四边形AEDF的周长为( )
A.12 cm
B.16 cm
C.20 cm
D.22 cm
B
6
如图,分别以Rt△ABC的斜边AB和直角边AC为边向△ABC外作等边三角形ABD和等边三角形ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠BAC=30°.给出以下结论:
①EF⊥AC;
②四边形ADFE为菱形;
③AD=4AG; ④FH= BD.
其中正确的结论是( )
A.①②③ B.①②④ C.①③④ D.②③④
C
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
菱形的判定方法:
归纳新知
互相垂直
四边形
课后练习
C
D
【答案】C
一组邻边相等
四边形
C
A
B
C
【答案】D
再 见
