2020-2021学年 人教版七年级数学下册 8.3.1 列二元一次方程组解和、差、倍、分问题 课件(49张)
文档属性
| 名称 | 2020-2021学年 人教版七年级数学下册 8.3.1 列二元一次方程组解和、差、倍、分问题 课件(49张) |  | |
| 格式 | pptx | ||
| 文件大小 | 600.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 12:42:41 | ||
图片预览











文档简介
第八章
8.3.1 列二元一次方程组解和、差、倍、分问题
人教版数学七年级下册
1
知识点
列二元一次方程组解决实际问题的步骤
1.用方程组解应用题的一般步骤:
(1)审题:弄清题意和题目中的___________;
(2)设元:用字母表示题目中的未知数,可________设未知数,也可________设未知数;
数量关系
直接
间接
合作探究
(3)列方程组:挖掘题中的所有条件,找出两个与未知数相关的__________,并依此列出__________;
(4)解方程组:利用______________或____________解所列方程组,求出未知数的值;
(5)检验作答:检验所求的解是否符合题目的实际意义,然后作答.
等量关系
方程组
代入消元法
加减消元法
2.小明买了50分和20分的邮票共16枚,花了5元9角钱,20分和50分的邮票各买了多少枚?根据题意完成下列各题:
(1)设小明买了20分的邮票x枚,则50分的邮票买了_____________枚,由题意可得一元一次方程:______________________.
(16-x)
20x+(16-x)×50=590
(2)设20分的邮票买了x枚,50分的邮票买了y枚,由题
意可得二元一次方程组
(3)设买20分的邮票花了x元,买50分的邮票花了y元,
由题意可得二元一次方程组
_________________.
x+y=16
20x+50y=590
_________________.
x+y=5.9
3.基本数量关系:各部分数量之和=全部数量;
较大量=较小量+多余量.
2
知识点
和、差、倍、分问题
4.等量关系:各部分数量之和不变.
?5.(中考·深圳)某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480个学生刚好住满.设大房间有x个,小房间有y个,下列方程组正确的是( )
A. B.
C. D.
x+y=70
8x+6y=480
x+y=70
6x+8y=480
x+y=480
6x+8y=70
x+y=480
8x+6y=70
A
6.(中考·泰安)夏季来临,某超市试销A,B两种型号的风扇,两周内共销售30台,销售收入5 300元,A型风扇每台200元,B型风扇每台150元,问A,B两种型号的风扇分别销售了多少台?若设A型风扇销售了x台,B型风扇销售了y台,则根据题意列出方程组为( )
A. B.
C. D.
x+y=5300
200x+150y=30
x+y=5300
150x+200y=30
x+y=30
200x+150y=5300
x+y=30
150x+200y=5300
C
7. (中考·十堰)我国古代数学著作《九章算术》卷七有下列问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价几何?”意思是:现在有几个人共同出钱去买件物品,如果每人出8钱,则剩余3钱;如果每人出7钱,则差4钱.问有多少人,物品的价格是多少?
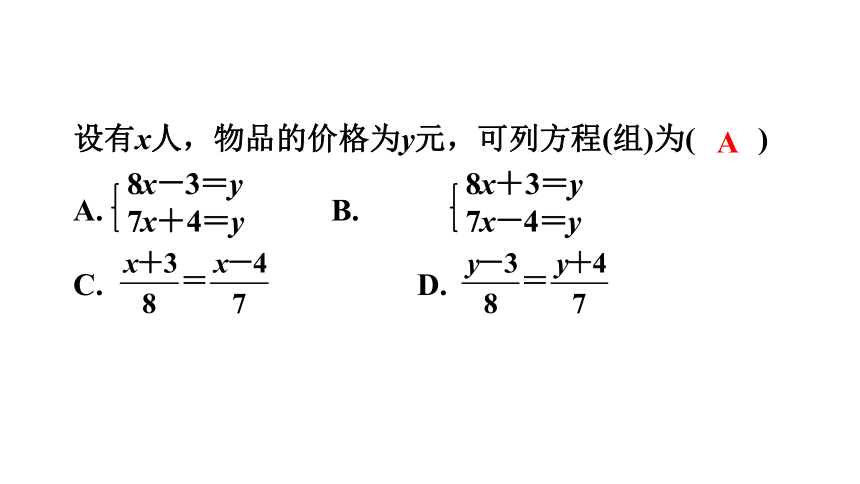
设有x人,物品的价格为y元,可列方程(组)为( )
A. B.
C. D.
8x-3=y
7x+4=y
8x+3=y
7x-4=y
A
8.(中考·济宁)《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的 ,那么乙也共有钱48文,甲、乙两人原来各有多少钱?设甲原有x文钱,乙原有y文
钱,可列方程组是
_________________.
9.如图①,在第一个天平上,物体A的质量等于物体B加上物体C的质量;如图②,在第二个天平上,物体A加上物体B的质量等于3个物体C的质量.请你判断:1个物体A与________个物体C的质量相等.
2
10. (中考·张家界)列方程解应用题.
《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元,求人数和羊价各是多少.
1
题型
盈余问题
设买羊人共有x人,羊价为y元.
由题意得 , 解得
答:买羊人共有21人,羊价为150元.
解:
y=5x+45
y=7x+3
x=21
y=150
11. (中考·吉林)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”设鸡x只,兔y只,可列方程组为( )
A. B.
C. D.
2
题型
“鸡兔同笼”问题
D
x+y=35
2x+2y=94
x+y=35
4x+2y=94
x+y=35
4x+4y=94
x+y=35
2x+4y=94
3
题型
图表信息问题
12.(中考·徐州)4月9日上午8时,2 017徐州国际马拉松赛鸣枪开跑,一名34岁的男子带着他的两个孩子一同参加了比赛,如图是两个孩子与记者的对话:
根据对话内容,请你用方程的知识帮记者求出哥哥和妹妹的年龄.
解:
设妹妹的年龄为x岁,哥哥的年龄为y岁.
根据题意得:
解得
答:哥哥的年龄是10岁,妹妹的年龄是6岁.
x=6
y=10
x+y=16
3(x+2)+(y+2) =34+2
13.(中考·张家界)某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后出售,所获利润全部捐给山区困难孩子,每件文化衫的批发价和零售价如下表:
假设文化衫全部售出,共获利1 860元,求黑白两种文化衫各有多少件.
解:
设黑色文化衫有x件,白色文化衫有y件.
依题意得:
解得
答:黑色文化衫有60件,白色文化衫有80件.
x=60
y=80
x+y=140
(25-10)x+(20-8)y=1860
4
题型
方案问题
14.(中考·连云港)某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房.
(1)求该店有客房多少间,房客多少人.
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何定房更合算?
(1)设该店有客房x间,房客y人.
根据题意,得
解得
答:该店有客房8间,房客63人.
解:
x=8
y=63
7x+7=y
9(x-1) =y
(2)若每间客房住4人,则63名房客至少需要客房16间,需付费20×16=320(钱);
若一次性定客房18间,则需付费20×18×0.8=288(钱).
288钱<320钱,
故选择一次性定客房18间更合算.
答:若诗中“众客”再次一起入住,他们选择一次性定客房18间更合算.
1.用方程组解应用题的一般步骤:
(1)审题:弄清题意和题目中的____________________;
(2)设元:用字母表示题目中的未知数,可________设未知数,也可________设未知数;
(3)列方程组:挖掘题中的所有条件,找出两个与未知数相关的__________,并依此列出_____________________;
数量关系(2) ;
直接
间接
等量关系
方程组
课后练习
(4)解方程组:利用______________或______________解所列方程组,求出未知数的值;
(5)检验作答:检验所求的解是否符合题目的实际意义,然后作答.
代入消元法
加减消元法
2.小明买了50分和20分的邮票共16枚,花了5元9角钱,20分和50分的邮票各买了多少枚?根据题意完成下列各题:
(1)设小明20分的邮票买了x枚,则50分的邮票买了___________枚,由题意可得一元一次方程_____________________.
(16-x)
20x+50(16-x)=590
(2)设20分的邮票买了x枚,50分的邮票买了y枚,由题意可得二元一次方程组___________________________.
(3)设买20分的邮票花了m元,买50分的邮票花了n元,由题意可得二元一次方程组_____________________.
3.基本数量关系:各部分数量之和=全部数量;
较大量=较小量+多余量.
4.等量关系:各部分数量之和不变.
*5.(2020·常德)今年新冠病毒疫情初期,口罩供应短缺,某地规定:每人每次限购5只.李红出门买口罩时,无论是否买到,都会消耗家里库存的口罩一只,如果有口罩买,他将买回5只.已知李红家原有库存15只,出门10次购买后,家里现有口罩35只.请问李红出门没有买到口罩的次数是________次.
【答案】4
6.(中考·泰安)夏季来临,某超市试销A,B两种型号的风扇,两周内共销售30台,销售收入5 300元,A型风扇每台200元,B型风扇每台150元,问A,B两种型号的风扇分别销售了多少台?若设A型风扇销售了x台,B型风扇销售了y台,则根据题意列出方程组为( )
【答案】C
【答案】A
A
A
10.(中考·张家界)列方程(组)解应用题.
《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元,求人数和羊价各是多少.
D
12.一次马拉松比赛中,一名34岁的男子带着他的两个孩子一同参加了比赛,如图是两个孩子与记者的对话:
根据对话内容,请你用方程的知识帮记者求出哥哥和妹妹的年龄.
13.(2020?徐州)本地某快递公司规定:寄件不超过1千克的部分按起步价计费;寄件超过1千克的部分按千克计费.小丽分别寄快递到上海和北京,收费标准及实际收费如下表:
收费标准
目的地
起步价/元
超过1千克的部分/(元/千克)
上海
a
b
北京
a+3
b+4
实际收费
目的地
质量/千克
费用/元
上海
2
9
北京
3
22
求a,b的值.
14.(中考?连云港)某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每1间客房住7人,那么有7人无房可住;如果每1间客房住9人,那么就空出1间客房.
(1)求该店有客房多少间,房客多少人.
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何定房更合算?
解:若每间客房住4人,则63名房客至少需要客房16间,需付费20×16=320(钱);
若一次性定客房18间,则需付费20×18×0.8=288(钱).
288钱<320钱,
故选择一次性定客房18间更合算.
答:若诗中“众客”再次一起入住,他们选择一次性定客房18间更合算.
再见
8.3.1 列二元一次方程组解和、差、倍、分问题
人教版数学七年级下册
1
知识点
列二元一次方程组解决实际问题的步骤
1.用方程组解应用题的一般步骤:
(1)审题:弄清题意和题目中的___________;
(2)设元:用字母表示题目中的未知数,可________设未知数,也可________设未知数;
数量关系
直接
间接
合作探究
(3)列方程组:挖掘题中的所有条件,找出两个与未知数相关的__________,并依此列出__________;
(4)解方程组:利用______________或____________解所列方程组,求出未知数的值;
(5)检验作答:检验所求的解是否符合题目的实际意义,然后作答.
等量关系
方程组
代入消元法
加减消元法
2.小明买了50分和20分的邮票共16枚,花了5元9角钱,20分和50分的邮票各买了多少枚?根据题意完成下列各题:
(1)设小明买了20分的邮票x枚,则50分的邮票买了_____________枚,由题意可得一元一次方程:______________________.
(16-x)
20x+(16-x)×50=590
(2)设20分的邮票买了x枚,50分的邮票买了y枚,由题
意可得二元一次方程组
(3)设买20分的邮票花了x元,买50分的邮票花了y元,
由题意可得二元一次方程组
_________________.
x+y=16
20x+50y=590
_________________.
x+y=5.9
3.基本数量关系:各部分数量之和=全部数量;
较大量=较小量+多余量.
2
知识点
和、差、倍、分问题
4.等量关系:各部分数量之和不变.
?5.(中考·深圳)某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480个学生刚好住满.设大房间有x个,小房间有y个,下列方程组正确的是( )
A. B.
C. D.
x+y=70
8x+6y=480
x+y=70
6x+8y=480
x+y=480
6x+8y=70
x+y=480
8x+6y=70
A
6.(中考·泰安)夏季来临,某超市试销A,B两种型号的风扇,两周内共销售30台,销售收入5 300元,A型风扇每台200元,B型风扇每台150元,问A,B两种型号的风扇分别销售了多少台?若设A型风扇销售了x台,B型风扇销售了y台,则根据题意列出方程组为( )
A. B.
C. D.
x+y=5300
200x+150y=30
x+y=5300
150x+200y=30
x+y=30
200x+150y=5300
x+y=30
150x+200y=5300
C
7. (中考·十堰)我国古代数学著作《九章算术》卷七有下列问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价几何?”意思是:现在有几个人共同出钱去买件物品,如果每人出8钱,则剩余3钱;如果每人出7钱,则差4钱.问有多少人,物品的价格是多少?
设有x人,物品的价格为y元,可列方程(组)为( )
A. B.
C. D.
8x-3=y
7x+4=y
8x+3=y
7x-4=y
A
8.(中考·济宁)《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的 ,那么乙也共有钱48文,甲、乙两人原来各有多少钱?设甲原有x文钱,乙原有y文
钱,可列方程组是
_________________.
9.如图①,在第一个天平上,物体A的质量等于物体B加上物体C的质量;如图②,在第二个天平上,物体A加上物体B的质量等于3个物体C的质量.请你判断:1个物体A与________个物体C的质量相等.
2
10. (中考·张家界)列方程解应用题.
《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元,求人数和羊价各是多少.
1
题型
盈余问题
设买羊人共有x人,羊价为y元.
由题意得 , 解得
答:买羊人共有21人,羊价为150元.
解:
y=5x+45
y=7x+3
x=21
y=150
11. (中考·吉林)我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”设鸡x只,兔y只,可列方程组为( )
A. B.
C. D.
2
题型
“鸡兔同笼”问题
D
x+y=35
2x+2y=94
x+y=35
4x+2y=94
x+y=35
4x+4y=94
x+y=35
2x+4y=94
3
题型
图表信息问题
12.(中考·徐州)4月9日上午8时,2 017徐州国际马拉松赛鸣枪开跑,一名34岁的男子带着他的两个孩子一同参加了比赛,如图是两个孩子与记者的对话:
根据对话内容,请你用方程的知识帮记者求出哥哥和妹妹的年龄.
解:
设妹妹的年龄为x岁,哥哥的年龄为y岁.
根据题意得:
解得
答:哥哥的年龄是10岁,妹妹的年龄是6岁.
x=6
y=10
x+y=16
3(x+2)+(y+2) =34+2
13.(中考·张家界)某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后出售,所获利润全部捐给山区困难孩子,每件文化衫的批发价和零售价如下表:
假设文化衫全部售出,共获利1 860元,求黑白两种文化衫各有多少件.
解:
设黑色文化衫有x件,白色文化衫有y件.
依题意得:
解得
答:黑色文化衫有60件,白色文化衫有80件.
x=60
y=80
x+y=140
(25-10)x+(20-8)y=1860
4
题型
方案问题
14.(中考·连云港)某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间客房.
(1)求该店有客房多少间,房客多少人.
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何定房更合算?
(1)设该店有客房x间,房客y人.
根据题意,得
解得
答:该店有客房8间,房客63人.
解:
x=8
y=63
7x+7=y
9(x-1) =y
(2)若每间客房住4人,则63名房客至少需要客房16间,需付费20×16=320(钱);
若一次性定客房18间,则需付费20×18×0.8=288(钱).
288钱<320钱,
故选择一次性定客房18间更合算.
答:若诗中“众客”再次一起入住,他们选择一次性定客房18间更合算.
1.用方程组解应用题的一般步骤:
(1)审题:弄清题意和题目中的____________________;
(2)设元:用字母表示题目中的未知数,可________设未知数,也可________设未知数;
(3)列方程组:挖掘题中的所有条件,找出两个与未知数相关的__________,并依此列出_____________________;
数量关系(2) ;
直接
间接
等量关系
方程组
课后练习
(4)解方程组:利用______________或______________解所列方程组,求出未知数的值;
(5)检验作答:检验所求的解是否符合题目的实际意义,然后作答.
代入消元法
加减消元法
2.小明买了50分和20分的邮票共16枚,花了5元9角钱,20分和50分的邮票各买了多少枚?根据题意完成下列各题:
(1)设小明20分的邮票买了x枚,则50分的邮票买了___________枚,由题意可得一元一次方程_____________________.
(16-x)
20x+50(16-x)=590
(2)设20分的邮票买了x枚,50分的邮票买了y枚,由题意可得二元一次方程组___________________________.
(3)设买20分的邮票花了m元,买50分的邮票花了n元,由题意可得二元一次方程组_____________________.
3.基本数量关系:各部分数量之和=全部数量;
较大量=较小量+多余量.
4.等量关系:各部分数量之和不变.
*5.(2020·常德)今年新冠病毒疫情初期,口罩供应短缺,某地规定:每人每次限购5只.李红出门买口罩时,无论是否买到,都会消耗家里库存的口罩一只,如果有口罩买,他将买回5只.已知李红家原有库存15只,出门10次购买后,家里现有口罩35只.请问李红出门没有买到口罩的次数是________次.
【答案】4
6.(中考·泰安)夏季来临,某超市试销A,B两种型号的风扇,两周内共销售30台,销售收入5 300元,A型风扇每台200元,B型风扇每台150元,问A,B两种型号的风扇分别销售了多少台?若设A型风扇销售了x台,B型风扇销售了y台,则根据题意列出方程组为( )
【答案】C
【答案】A
A
A
10.(中考·张家界)列方程(组)解应用题.
《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”题意是:若干人共同出资买羊,每人出5元,则差45元;每人出7元,则差3元,求人数和羊价各是多少.
D
12.一次马拉松比赛中,一名34岁的男子带着他的两个孩子一同参加了比赛,如图是两个孩子与记者的对话:
根据对话内容,请你用方程的知识帮记者求出哥哥和妹妹的年龄.
13.(2020?徐州)本地某快递公司规定:寄件不超过1千克的部分按起步价计费;寄件超过1千克的部分按千克计费.小丽分别寄快递到上海和北京,收费标准及实际收费如下表:
收费标准
目的地
起步价/元
超过1千克的部分/(元/千克)
上海
a
b
北京
a+3
b+4
实际收费
目的地
质量/千克
费用/元
上海
2
9
北京
3
22
求a,b的值.
14.(中考?连云港)某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每1间客房住7人,那么有7人无房可住;如果每1间客房住9人,那么就空出1间客房.
(1)求该店有客房多少间,房客多少人.
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何定房更合算?
解:若每间客房住4人,则63名房客至少需要客房16间,需付费20×16=320(钱);
若一次性定客房18间,则需付费20×18×0.8=288(钱).
288钱<320钱,
故选择一次性定客房18间更合算.
答:若诗中“众客”再次一起入住,他们选择一次性定客房18间更合算.
再见
