六年级下册数学课件-3.3 反比例西师大版(共19张PPT)
文档属性
| 名称 | 六年级下册数学课件-3.3 反比例西师大版(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 346.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 06:07:25 | ||
图片预览






文档简介
(共19张PPT)
反
比
例
第1课时
六年级下册第三单元
成正比例的量有什么特征?
(1)两种相关联的量,一种量变化,另一种量也随着相应的变化。
(2)两种量中相对应的两个量的比值(商)
一定。
复习引入
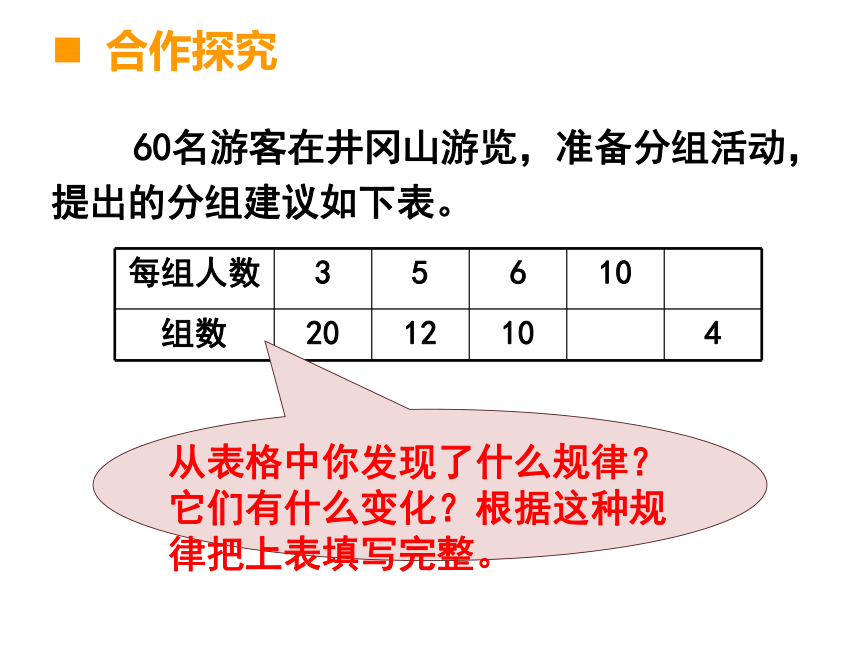
每组人数
3
5
6
10
组数
20
12
10
4
60名游客在井冈山游览,准备分组活动,提出的分组建议如下表。
从表格中你发现了什么规律?它们有什么变化?根据这种规律把上表填写完整。
合作探究
(
)和(
)是两种相关联的量,每组人数(
),组数反而(
),每组人数(
),组数反而(
)。
规律是:每组人数和组数的(
)是一定的。
合作探究
每组人数
组数
扩大
缩小
乘积
缩小
扩大
每组人数
3
5
6
10
组数
20
12
10
4
60名游客在井冈山游览,准备分组活动,提出的分组建议如下表。
15
6
合作探究
每分打字(个)
120
100
75
60
所需时间(分)
25
30
60
50
50
40
这篇稿子,每分钟打120个字,25分能够打完。
探索规律,并按规律填表。再说一说你发现的规律。
合作探究
合作探究
每分钟打的字数和所用的时间是两个相关的量。
每分钟打字的数量扩大,所用的时间反而缩小。
每分钟打字的数量缩小,所用的时间反而扩大。
每分钟打字的数量和所用的时间乘积一定。
从上面二个例子中,你发现了什么?
题中两个量是两种相关联的量中,相对应的两个数的乘积是一定的。
两种相关联的量,一种量扩大或缩小若干倍,另一种量反而缩小或扩大相同的倍数。
像这样的两种量,叫做成反比例的量,它们的关系叫反比例关系。
展示交流
每组人数×组数=游客总人数
(积一定)
每分钟打的字数×时间=稿件总字数(积一定)
展示交流
写一写刚才上面两道题的关系
如何判断两个量是否成反比例?
1.是两种相关联的量,一种量随着另一种量变化。
2.变化方向相反,一种量扩大(缩小)另一种量反而缩小(扩大)。
3.相对应的两个量的乘积是一定的。
课堂
课堂练习
判一判:
1.当速度一定,路程和时间成什么比例?
为什么?
2.当时间一定,路程和速度成什么比例?
为什么?
3.当路程一定,速度和时间成什么比例?
为什么?
判断下面各题中的两种量是否比例。如成比例,成什么比例?
(1)报纸的单价一定,订阅的份数与总价。
(2)圆柱的体积一定,它的底面积和高。
(3)运动员跳高的高度和他的身高。
(4)一筐桃平均分给猴子,猴的只数和每只猴分桃的个数。
(5)圆的面积和它的半径。
(6)C
=4a,C
和a。
成反比例
成反比例
不成比例
成正比例
不成比例
成正比例
课堂练习
课堂探索
“青年突击队”参加泥石流抢险,原计划每时行6km,要4时才能到达目的地。出发时接到紧急通知要求3时到达,他们平均每时需要行多少千米?
你怎样解决这一问题?
课堂探索
合作要求:
(1)先自己独立思考,并动手试一试。
(2)完成后在小组内交流、讨论。
(每人都要说一说自己的想法)
(3)小组长选好本组汇报的人。
(4)指名汇报,全班交流。
课堂探索
解:设他们平均每小时行x
km。
3x
=
6×4
x
=24÷3
x
=8
答:他们每时行8km。
课堂练习
一辆汽车从甲地开往乙地,每时行70km,5时到达。如果每时行驶87.5km,需要多少时到达?
解:需要x时到达。
87.5x
=
70×5
x
=350÷87.5
x
=4
答:需要4时到达。
老师要放大招,怕不怕?
拓展练习
修一条路,原计划每天修400m,25天完成。实际前4天修200m,照这样的速度,修完要用多少天?
解:修完要用x天。
(200÷4)x
=
400×25
x
=10000÷50
x
=200
答:修完需要200天。
通过这节课的学习,你学到了什么?
课堂总结
反
比
例
第1课时
六年级下册第三单元
成正比例的量有什么特征?
(1)两种相关联的量,一种量变化,另一种量也随着相应的变化。
(2)两种量中相对应的两个量的比值(商)
一定。
复习引入
每组人数
3
5
6
10
组数
20
12
10
4
60名游客在井冈山游览,准备分组活动,提出的分组建议如下表。
从表格中你发现了什么规律?它们有什么变化?根据这种规律把上表填写完整。
合作探究
(
)和(
)是两种相关联的量,每组人数(
),组数反而(
),每组人数(
),组数反而(
)。
规律是:每组人数和组数的(
)是一定的。
合作探究
每组人数
组数
扩大
缩小
乘积
缩小
扩大
每组人数
3
5
6
10
组数
20
12
10
4
60名游客在井冈山游览,准备分组活动,提出的分组建议如下表。
15
6
合作探究
每分打字(个)
120
100
75
60
所需时间(分)
25
30
60
50
50
40
这篇稿子,每分钟打120个字,25分能够打完。
探索规律,并按规律填表。再说一说你发现的规律。
合作探究
合作探究
每分钟打的字数和所用的时间是两个相关的量。
每分钟打字的数量扩大,所用的时间反而缩小。
每分钟打字的数量缩小,所用的时间反而扩大。
每分钟打字的数量和所用的时间乘积一定。
从上面二个例子中,你发现了什么?
题中两个量是两种相关联的量中,相对应的两个数的乘积是一定的。
两种相关联的量,一种量扩大或缩小若干倍,另一种量反而缩小或扩大相同的倍数。
像这样的两种量,叫做成反比例的量,它们的关系叫反比例关系。
展示交流
每组人数×组数=游客总人数
(积一定)
每分钟打的字数×时间=稿件总字数(积一定)
展示交流
写一写刚才上面两道题的关系
如何判断两个量是否成反比例?
1.是两种相关联的量,一种量随着另一种量变化。
2.变化方向相反,一种量扩大(缩小)另一种量反而缩小(扩大)。
3.相对应的两个量的乘积是一定的。
课堂
课堂练习
判一判:
1.当速度一定,路程和时间成什么比例?
为什么?
2.当时间一定,路程和速度成什么比例?
为什么?
3.当路程一定,速度和时间成什么比例?
为什么?
判断下面各题中的两种量是否比例。如成比例,成什么比例?
(1)报纸的单价一定,订阅的份数与总价。
(2)圆柱的体积一定,它的底面积和高。
(3)运动员跳高的高度和他的身高。
(4)一筐桃平均分给猴子,猴的只数和每只猴分桃的个数。
(5)圆的面积和它的半径。
(6)C
=4a,C
和a。
成反比例
成反比例
不成比例
成正比例
不成比例
成正比例
课堂练习
课堂探索
“青年突击队”参加泥石流抢险,原计划每时行6km,要4时才能到达目的地。出发时接到紧急通知要求3时到达,他们平均每时需要行多少千米?
你怎样解决这一问题?
课堂探索
合作要求:
(1)先自己独立思考,并动手试一试。
(2)完成后在小组内交流、讨论。
(每人都要说一说自己的想法)
(3)小组长选好本组汇报的人。
(4)指名汇报,全班交流。
课堂探索
解:设他们平均每小时行x
km。
3x
=
6×4
x
=24÷3
x
=8
答:他们每时行8km。
课堂练习
一辆汽车从甲地开往乙地,每时行70km,5时到达。如果每时行驶87.5km,需要多少时到达?
解:需要x时到达。
87.5x
=
70×5
x
=350÷87.5
x
=4
答:需要4时到达。
老师要放大招,怕不怕?
拓展练习
修一条路,原计划每天修400m,25天完成。实际前4天修200m,照这样的速度,修完要用多少天?
解:修完要用x天。
(200÷4)x
=
400×25
x
=10000÷50
x
=200
答:修完需要200天。
通过这节课的学习,你学到了什么?
课堂总结
