华师大版九年级下第27章二次函数单元测试(2套)(无答案)
文档属性
| 名称 | 华师大版九年级下第27章二次函数单元测试(2套)(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 798.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-17 09:44:09 | ||
图片预览



文档简介
九年级数学二次函数测试卷
一、选择题:每小题3分,共15分.每小题给出四个答案,其中只有一个是正确的.
1.下抛物线的开口方向、对称轴、顶点坐标分别是( )
A、开口向上;x=-3;(-3,5) B、开口向上;x=3;(3,5)
C、开口向下;x=3;(-3,-5) D、开口向下;x=-3;(3,-5)
2. 抛物线y=x2+3x的顶点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3. 二次函数的图象如图,那么abc、2a+b、a+b+c、a-b+c 这四个代数式中,值为正数的有( )
A.4个 B.3个 C.2个 D.1个
4. 抛物线y=x2-2x-3与轴两交点间的距离是( );
A.4 B.3 C.2 D.1
5. 已知反比例函数的图象如右图所示,则二次函数的图象大致为( )
二、填空题:(每小题4分,共20分).
6. 当m 时,函数是二次函数.
7.已知以x为自变量的二次函数y=(m-2)x2+m2-m-2的图象经过原点,则m= ,当x 时y随x增大而减小.
8.若点A(-5,y1)、B(2,y2)都在y=2x2上,则____(填“>”或“<”)
9. 若函数有最小值是3,则= ;二次函数的值永远是 数;
10. 初三数学课本上,用“描点法”画二次函数的图象时,列了如下表格:
… 0 1 2 …
… …
根据表格上的信息回答问题:该二次函数在时 .
三、解答题:(每小题6分,共30分)
11.已知抛物线的顶点是(-1,-2),且过点(1,10)。求此抛物线对应的二次函数关系式.
12. 已知抛物线过三点:(0,-2),(1,0),(2,3). 求此抛物线对应的二次函数关系式.
13.已知抛物线y=x2+x-.试求它的顶点坐标和对称轴。
14.用一根长40m的篱笆围成一个矩形场地,长和宽分别为多少时,面积最大?
15.求二次函数y=x2-2x-1二次函数的图象与x轴的交点坐标.
四、解答题(每小题7分,共28分)。
16.已知函数的部分图象如图所示,
(1)写出抛物线与x轴的另外一个交点坐标并求c值;
(2)观察图像直接写出不等式的解集
第16题图 第17题图 第18题图
17.已知,如图,直线经过和两点,它与抛物线在第一象限内相交于点P,又知的面积为,求的值;
18如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m。
(1)在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
19.汽车在行驶中,由于惯力作用,刹车后还要向前滑行一段距离才能停住,我们称这段距离为“刹车距离”,刹车距离是分析事故的一个重要因素,在一个限速40乙内的弯道上,甲、乙两车相向而行,发现情况不对,同时刹车,但还是相碰了,事后现场测量甲车的刹车距离为12m,乙车的刹车距离超过10m,但小于20m,查有关资料知,甲种车的刹车距离S甲(m)与车速x()之间有下列关系,S甲=0.1x+0.01x2,乙种车的刹车距离S乙(m)与车速x()的关系如下图表示,请你就两车的速度方面分析相碰的原因。
五.解答题:(每小题9分,共27分)。
20.2000年度东风公司神鹰汽车改装厂开发出A型农用车,其成本价为每辆2万元,出厂价为每辆2.4万元,年销售量为10000辆,2001年为了支援西部大开发的生态农业建设,该厂抓住机遇,发展企业,全面提高A型农用车的科技含量,每辆农用车的成本价增长率为x,出厂价增长率为0.75x,预测年销售增长率为0.6x.(年利润=(出厂价-成本价)×年销售量)
(1)求2001年度该厂销售A型农用车的年利润y(万元)与x之间的函数关系。
(2)该厂要是2001年度销售A型农用车的年利润达到4028万元,该年度A型农用车的年销售量应该是多少辆?(6分)
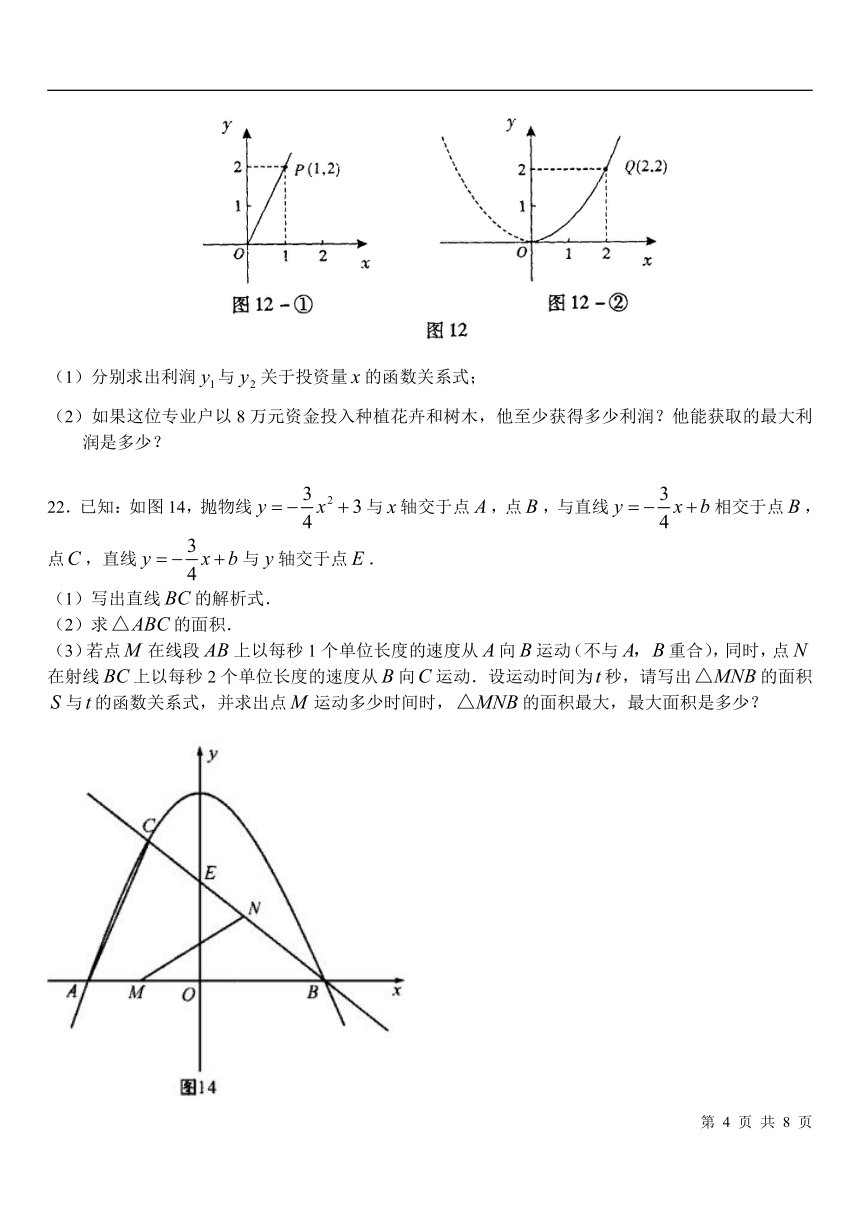
21.随着鹅城惠州近几年城市建设的快速发展,对花木的需求量逐年提高。某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润与投资量成正比例关系,如图12-①所示;种植花卉的利润与投资量成二次函数关系,如图12-②所示(注:利润与投资量的单位:万元)
(1)分别求出利润与关于投资量的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
22.已知:如图14,抛物线与轴交于点,点,与直线相交于点,点,直线与轴交于点.
(1)写出直线的解析式.
(2)求的面积.
(3)若点在线段上以每秒1个单位长度的速度从向运动(不与重合),同时,点在射线上以每秒2个单位长度的速度从向运动.设运动时间为秒,请写出的面积与的函数关系式,并求出点运动多少时间时,的面积最大,最大面积是多少?
华师大版九年级(下)二次函数学习评价
一、精心选一选(每题4分,共16分)
1.抛物线y=x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为( )
A .y=x2+2x-2 B. y=x2+2x+1
C. y=x2-2x-1 D .y=x2-2x+1
2.已知二次函数y=ax2+bx+c的图象如右图所示,则一次函数y=ax+bc 的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.直线y=ax+b与抛物线y=ax2+bx+c 中,a、b异号 ,b c<0, 那么
它们在同一坐标系中的图象大致为( )
4、过原点的抛物线是( )
A y=2x2+x B C y=2x2-1 D y=2x2+1
5、已知二次函数,当x=3时,y的值为( )
A 4 B -4 C 3 D -3
6、设抛物线y=x2+8x-k的顶点在x轴上,则k的值为( )
A -16 B 16 C -8 D 8
二、耐心填一填(每题4分,共40分)
5.函数y=(m+3),当m= 时,它的图象是抛物线.
6.抛物线y=(x-3)2-1开口向 ,顶点坐标是 ,对称轴是 .
7.已知以x为自变量的二次函数y=(m-2)x2+m2-m-2的图象经过原点,则m= ,当x 时y随x增大而减小.
8.函数y=2x2-7x+3顶点坐标为 .
9.抛物线y=x2+bx+c,经过A(-1,0)、B(3,0)两点,则这条抛物线的解析式为 ,它的对称轴为 .
10.抛物线y=x2+bx+c的顶点为(2,3),则b= ,c= .
11.如果抛物线y=ax2+bx+c的对称轴是x=—2,且开口方向,形状与抛物线y=—x2相同,且过原点,那么a= ,b= ,c= .
12.直线y=-3x+2与抛物线y=x2-x+3的交点有 个,交点坐标为
13.抛物线的顶点是C(2,),它与x轴交于A、B两点,它们的横坐标是方程x2-4x+3=0的两个根,则AB= ,S△ABC= .
14.抛物线y=x2+bx+4与x轴只有一个交点则b= ;当x 时y>0.
三、细心解一解(第20题9分,其余每题7分,共44分)
15.如图二次函数y=ax2+bx+c的图象经过A 、B、C
三点,
(1)观察图象,写出A 、B、C三点的坐标,
并求出抛物线解析式,
(2)求此抛物线的顶点坐标和对称轴
(3)观察图象,当x取何值时,y<0?y=0?y>0
16.函数y=ax2+bx+c(其中a、b、c为常数,a≠0),图象如图
所示,x=为该函数图象的对称轴,根据这个函数图象,你能
得到关于该函数的哪些性质和结论?(写出四个即可)
17.某市近年来经济发展速度很快,根据统计:该市国内生产总值1990年为8.6亿元人民币,1995年为10.4亿元人民币,2000年为12.9亿元人民币.经论证:上述数据适合一个二次函数关系,请你根据这个函数关系,预测2005年该市国内生产总值将达到多少?
18.已知二次函数y=(m2-2)x2-4mx+n的图象关于直线x=2对称,且它的最高点在直线y=x+1上.
(1)求此二次函数的解析式;
(2)若此抛物线的开口方向不变,顶点在直线y=x+1上移动到点M时,图象与x轴交于A 、B两点,且S△ABM=8,求此时的二次函数的解析式.
19.如图(1)是棱长为a的小正方体,图(2),图(3)由这样的小正方体摆放而成,按照这样的方法继续摆放,自上而下,分别叫做第一层、第二层、第三层、… 、第n层,第n层的小正方体的个数记为s,解答下列问题:
(1)按照要求填表:
n 1 2 3 4 ……
s 1 3 6 ……
(2)写出当n=10时,S= ;
(3)根据上表中的数据,把S作为纵坐标,n作为横坐标,在平面直角坐标系中,描出相应的各点;
(4)请你猜一猜上述各点会在某一个函数图象上吗?如果在某一函数的图象上,求出该函数的解析式.
20.在平面直角坐标系中,给定以下五点A(-2,0),B(1,0),C(4,0),D(-2,),E(0,6),从这五点中选取三点,使经过这三点的抛物线满足以平行于y轴的直线为对称轴.我们约定:把经过三点A、E、B的抛物线表示为抛物线AEB(如图所示)
(1)问符合条件的抛物线还有哪几条?不求解析式请用约定的方法表示出来;
(2)在(1)中是否存在这样的一条抛物线,它与余下的两点所确定的直线不相交?如果存在,试求抛物线及直线的解析式:如果不存在,请说明理由.
21、已知抛物线与x轴交于点M(-1,0)、N(2,0),且经过点(1,2),求这个函数的表达式;
22、已知抛物线的顶点为(1,-1),且过点(2,1),求这个函数的表达式;
23、已知一个二次函数的图象经过点(1,-1),(0,1),(-1,13),求这个二次函数的解析式;
24、某工厂现有80台机器,每台机器平均每天生产384件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,由于其他生产条件没变,因此每增加一台机器,每台机器平均每天将少生产4件产品.
(1)如果增加x台机器,每天的生产总量为y件,请你写出y与x之间的关系式;
(2)增加多少台机器,可以使每天的生产总量最大?最大生产总量是多少?
25、已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上, 分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
(1)用含y的代数式表示AE.
(2)求y与x之间的函数关系式,并求出x的取值范围.
(3)设四边形DECF的面积为S,求出S的最大值.
A B C D
C.
-1
4
y
x
A
B
5
O
x
1
-1
-1
1 2
y
O
E
x
y
D
O
B
A
C
D
C
B
F
E
A
第 5 页 共 8 页
一、选择题:每小题3分,共15分.每小题给出四个答案,其中只有一个是正确的.
1.下抛物线的开口方向、对称轴、顶点坐标分别是( )
A、开口向上;x=-3;(-3,5) B、开口向上;x=3;(3,5)
C、开口向下;x=3;(-3,-5) D、开口向下;x=-3;(3,-5)
2. 抛物线y=x2+3x的顶点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3. 二次函数的图象如图,那么abc、2a+b、a+b+c、a-b+c 这四个代数式中,值为正数的有( )
A.4个 B.3个 C.2个 D.1个
4. 抛物线y=x2-2x-3与轴两交点间的距离是( );
A.4 B.3 C.2 D.1
5. 已知反比例函数的图象如右图所示,则二次函数的图象大致为( )
二、填空题:(每小题4分,共20分).
6. 当m 时,函数是二次函数.
7.已知以x为自变量的二次函数y=(m-2)x2+m2-m-2的图象经过原点,则m= ,当x 时y随x增大而减小.
8.若点A(-5,y1)、B(2,y2)都在y=2x2上,则____(填“>”或“<”)
9. 若函数有最小值是3,则= ;二次函数的值永远是 数;
10. 初三数学课本上,用“描点法”画二次函数的图象时,列了如下表格:
… 0 1 2 …
… …
根据表格上的信息回答问题:该二次函数在时 .
三、解答题:(每小题6分,共30分)
11.已知抛物线的顶点是(-1,-2),且过点(1,10)。求此抛物线对应的二次函数关系式.
12. 已知抛物线过三点:(0,-2),(1,0),(2,3). 求此抛物线对应的二次函数关系式.
13.已知抛物线y=x2+x-.试求它的顶点坐标和对称轴。
14.用一根长40m的篱笆围成一个矩形场地,长和宽分别为多少时,面积最大?
15.求二次函数y=x2-2x-1二次函数的图象与x轴的交点坐标.
四、解答题(每小题7分,共28分)。
16.已知函数的部分图象如图所示,
(1)写出抛物线与x轴的另外一个交点坐标并求c值;
(2)观察图像直接写出不等式的解集
第16题图 第17题图 第18题图
17.已知,如图,直线经过和两点,它与抛物线在第一象限内相交于点P,又知的面积为,求的值;
18如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m。
(1)在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
19.汽车在行驶中,由于惯力作用,刹车后还要向前滑行一段距离才能停住,我们称这段距离为“刹车距离”,刹车距离是分析事故的一个重要因素,在一个限速40乙内的弯道上,甲、乙两车相向而行,发现情况不对,同时刹车,但还是相碰了,事后现场测量甲车的刹车距离为12m,乙车的刹车距离超过10m,但小于20m,查有关资料知,甲种车的刹车距离S甲(m)与车速x()之间有下列关系,S甲=0.1x+0.01x2,乙种车的刹车距离S乙(m)与车速x()的关系如下图表示,请你就两车的速度方面分析相碰的原因。
五.解答题:(每小题9分,共27分)。
20.2000年度东风公司神鹰汽车改装厂开发出A型农用车,其成本价为每辆2万元,出厂价为每辆2.4万元,年销售量为10000辆,2001年为了支援西部大开发的生态农业建设,该厂抓住机遇,发展企业,全面提高A型农用车的科技含量,每辆农用车的成本价增长率为x,出厂价增长率为0.75x,预测年销售增长率为0.6x.(年利润=(出厂价-成本价)×年销售量)
(1)求2001年度该厂销售A型农用车的年利润y(万元)与x之间的函数关系。
(2)该厂要是2001年度销售A型农用车的年利润达到4028万元,该年度A型农用车的年销售量应该是多少辆?(6分)
21.随着鹅城惠州近几年城市建设的快速发展,对花木的需求量逐年提高。某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润与投资量成正比例关系,如图12-①所示;种植花卉的利润与投资量成二次函数关系,如图12-②所示(注:利润与投资量的单位:万元)
(1)分别求出利润与关于投资量的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
22.已知:如图14,抛物线与轴交于点,点,与直线相交于点,点,直线与轴交于点.
(1)写出直线的解析式.
(2)求的面积.
(3)若点在线段上以每秒1个单位长度的速度从向运动(不与重合),同时,点在射线上以每秒2个单位长度的速度从向运动.设运动时间为秒,请写出的面积与的函数关系式,并求出点运动多少时间时,的面积最大,最大面积是多少?
华师大版九年级(下)二次函数学习评价
一、精心选一选(每题4分,共16分)
1.抛物线y=x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为( )
A .y=x2+2x-2 B. y=x2+2x+1
C. y=x2-2x-1 D .y=x2-2x+1
2.已知二次函数y=ax2+bx+c的图象如右图所示,则一次函数y=ax+bc 的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.直线y=ax+b与抛物线y=ax2+bx+c 中,a、b异号 ,b c<0, 那么
它们在同一坐标系中的图象大致为( )
4、过原点的抛物线是( )
A y=2x2+x B C y=2x2-1 D y=2x2+1
5、已知二次函数,当x=3时,y的值为( )
A 4 B -4 C 3 D -3
6、设抛物线y=x2+8x-k的顶点在x轴上,则k的值为( )
A -16 B 16 C -8 D 8
二、耐心填一填(每题4分,共40分)
5.函数y=(m+3),当m= 时,它的图象是抛物线.
6.抛物线y=(x-3)2-1开口向 ,顶点坐标是 ,对称轴是 .
7.已知以x为自变量的二次函数y=(m-2)x2+m2-m-2的图象经过原点,则m= ,当x 时y随x增大而减小.
8.函数y=2x2-7x+3顶点坐标为 .
9.抛物线y=x2+bx+c,经过A(-1,0)、B(3,0)两点,则这条抛物线的解析式为 ,它的对称轴为 .
10.抛物线y=x2+bx+c的顶点为(2,3),则b= ,c= .
11.如果抛物线y=ax2+bx+c的对称轴是x=—2,且开口方向,形状与抛物线y=—x2相同,且过原点,那么a= ,b= ,c= .
12.直线y=-3x+2与抛物线y=x2-x+3的交点有 个,交点坐标为
13.抛物线的顶点是C(2,),它与x轴交于A、B两点,它们的横坐标是方程x2-4x+3=0的两个根,则AB= ,S△ABC= .
14.抛物线y=x2+bx+4与x轴只有一个交点则b= ;当x 时y>0.
三、细心解一解(第20题9分,其余每题7分,共44分)
15.如图二次函数y=ax2+bx+c的图象经过A 、B、C
三点,
(1)观察图象,写出A 、B、C三点的坐标,
并求出抛物线解析式,
(2)求此抛物线的顶点坐标和对称轴
(3)观察图象,当x取何值时,y<0?y=0?y>0
16.函数y=ax2+bx+c(其中a、b、c为常数,a≠0),图象如图
所示,x=为该函数图象的对称轴,根据这个函数图象,你能
得到关于该函数的哪些性质和结论?(写出四个即可)
17.某市近年来经济发展速度很快,根据统计:该市国内生产总值1990年为8.6亿元人民币,1995年为10.4亿元人民币,2000年为12.9亿元人民币.经论证:上述数据适合一个二次函数关系,请你根据这个函数关系,预测2005年该市国内生产总值将达到多少?
18.已知二次函数y=(m2-2)x2-4mx+n的图象关于直线x=2对称,且它的最高点在直线y=x+1上.
(1)求此二次函数的解析式;
(2)若此抛物线的开口方向不变,顶点在直线y=x+1上移动到点M时,图象与x轴交于A 、B两点,且S△ABM=8,求此时的二次函数的解析式.
19.如图(1)是棱长为a的小正方体,图(2),图(3)由这样的小正方体摆放而成,按照这样的方法继续摆放,自上而下,分别叫做第一层、第二层、第三层、… 、第n层,第n层的小正方体的个数记为s,解答下列问题:
(1)按照要求填表:
n 1 2 3 4 ……
s 1 3 6 ……
(2)写出当n=10时,S= ;
(3)根据上表中的数据,把S作为纵坐标,n作为横坐标,在平面直角坐标系中,描出相应的各点;
(4)请你猜一猜上述各点会在某一个函数图象上吗?如果在某一函数的图象上,求出该函数的解析式.
20.在平面直角坐标系中,给定以下五点A(-2,0),B(1,0),C(4,0),D(-2,),E(0,6),从这五点中选取三点,使经过这三点的抛物线满足以平行于y轴的直线为对称轴.我们约定:把经过三点A、E、B的抛物线表示为抛物线AEB(如图所示)
(1)问符合条件的抛物线还有哪几条?不求解析式请用约定的方法表示出来;
(2)在(1)中是否存在这样的一条抛物线,它与余下的两点所确定的直线不相交?如果存在,试求抛物线及直线的解析式:如果不存在,请说明理由.
21、已知抛物线与x轴交于点M(-1,0)、N(2,0),且经过点(1,2),求这个函数的表达式;
22、已知抛物线的顶点为(1,-1),且过点(2,1),求这个函数的表达式;
23、已知一个二次函数的图象经过点(1,-1),(0,1),(-1,13),求这个二次函数的解析式;
24、某工厂现有80台机器,每台机器平均每天生产384件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,由于其他生产条件没变,因此每增加一台机器,每台机器平均每天将少生产4件产品.
(1)如果增加x台机器,每天的生产总量为y件,请你写出y与x之间的关系式;
(2)增加多少台机器,可以使每天的生产总量最大?最大生产总量是多少?
25、已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上, 分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
(1)用含y的代数式表示AE.
(2)求y与x之间的函数关系式,并求出x的取值范围.
(3)设四边形DECF的面积为S,求出S的最大值.
A B C D
C.
-1
4
y
x
A
B
5
O
x
1
-1
-1
1 2
y
O
E
x
y
D
O
B
A
C
D
C
B
F
E
A
第 5 页 共 8 页
