8.3 完全平方公式与完全平方差公式 课时训练(含答案)
文档属性
| 名称 | 8.3 完全平方公式与完全平方差公式 课时训练(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 18:52:25 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
8.3完全平方公式与完全平方差公式课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知可以写成一个完全平方式,则的值为( )
A. B.3 C.6 D.9
2.将多项式加上一个单项式后,使它能成为一个完全平方式,下列添加单项式错误的是( )
A. B. C. D.
3.若的值为,则的值为( )
A. B. C. D.
4.设,,,,其中①当时,.②当时,.则下列正确的是( )
A.①正确②错误 B.①正确②正确
C.①错误②正确 D.①错误②错误
5.在括号内填上适当的单项式,使成为完全平方式应填( )
A. B. C. D.
6.如果两数和的平方的结果是,那么的值是( )
A. B.或 C.或 D.
7.已知,,则的值为( )
A.3 B.6 C.12 D.18
8.如图,从边长为的正方形纸片中剪去一个边长为的正方形(),剩余部分沿虚线又剪拼成一个长方形(既没有重叠也没有缝隙),则长方形的面积为( )
A. B. C. D.
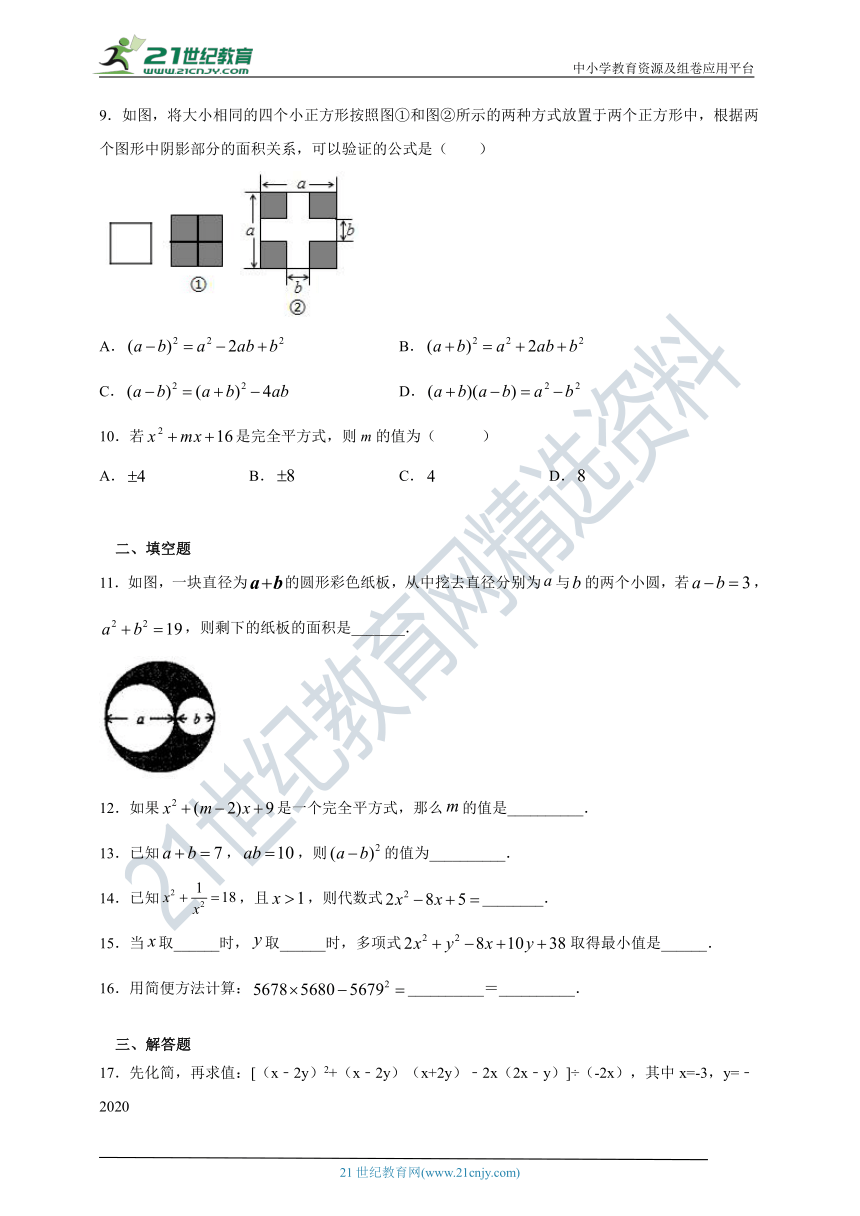
9.如图,将大小相同的四个小正方形按照图①和图②所示的两种方式放置于两个正方形中,根据两个图形中阴影部分的面积关系,可以验证的公式是( )
A. B.
C. D.
10.若是完全平方式,则m的值为( )
A. B. C. D.
二、填空题
11.如图,一块直径为的圆形彩色纸板,从中挖去直径分别为与的两个小圆,若,,则剩下的纸板的面积是_______.
12.如果是一个完全平方式,那么的值是__________.
13.已知,,则的值为__________.
14.已知,且,则代数式________.
15.当取______时,取______时,多项式取得最小值是______.
16.用简便方法计算:__________=__________.
三、解答题
17.先化简,再求值:[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷(-2x),其中x=-3,y=﹣2020
18.(1)计算:.
(2)先化简,再求值:,其中.
19.已知:,求代数式的值.
20.阅读下列材料:
规定一种新运算:.例如:,按照这种运算的规定,请解答下列问题:
(1)用含的式子表示;
(2)当,求的值;
(3)若,求的值.
参考答案
1.D
2.A
3.B
4.B
5.C
6.B
7.B
8.B
9.A
10.B
11.
12.或
13.
14.7
15.2 -5 5
16.(5679-1)(5679+1)-56792 -1
17.;-2023
解:[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷(-2x)
=
.
当x=﹣3,y=﹣2020时,
原式=.
18.(1)5;(2),
解:(1)原式
;
(2)
,
当时,原式.
19.-32
解:原式,
,
原式.
20.(1);(2);(3)
解:(1)∵
∴;
(2)∵.
.
.
(3)∵
∴
又∵,
,
解得: ,
_21?????????è?????(www.21cnjy.com)_
8.3完全平方公式与完全平方差公式课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知可以写成一个完全平方式,则的值为( )
A. B.3 C.6 D.9
2.将多项式加上一个单项式后,使它能成为一个完全平方式,下列添加单项式错误的是( )
A. B. C. D.
3.若的值为,则的值为( )
A. B. C. D.
4.设,,,,其中①当时,.②当时,.则下列正确的是( )
A.①正确②错误 B.①正确②正确
C.①错误②正确 D.①错误②错误
5.在括号内填上适当的单项式,使成为完全平方式应填( )
A. B. C. D.
6.如果两数和的平方的结果是,那么的值是( )
A. B.或 C.或 D.
7.已知,,则的值为( )
A.3 B.6 C.12 D.18
8.如图,从边长为的正方形纸片中剪去一个边长为的正方形(),剩余部分沿虚线又剪拼成一个长方形(既没有重叠也没有缝隙),则长方形的面积为( )
A. B. C. D.
9.如图,将大小相同的四个小正方形按照图①和图②所示的两种方式放置于两个正方形中,根据两个图形中阴影部分的面积关系,可以验证的公式是( )
A. B.
C. D.
10.若是完全平方式,则m的值为( )
A. B. C. D.
二、填空题
11.如图,一块直径为的圆形彩色纸板,从中挖去直径分别为与的两个小圆,若,,则剩下的纸板的面积是_______.
12.如果是一个完全平方式,那么的值是__________.
13.已知,,则的值为__________.
14.已知,且,则代数式________.
15.当取______时,取______时,多项式取得最小值是______.
16.用简便方法计算:__________=__________.
三、解答题
17.先化简,再求值:[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷(-2x),其中x=-3,y=﹣2020
18.(1)计算:.
(2)先化简,再求值:,其中.
19.已知:,求代数式的值.
20.阅读下列材料:
规定一种新运算:.例如:,按照这种运算的规定,请解答下列问题:
(1)用含的式子表示;
(2)当,求的值;
(3)若,求的值.
参考答案
1.D
2.A
3.B
4.B
5.C
6.B
7.B
8.B
9.A
10.B
11.
12.或
13.
14.7
15.2 -5 5
16.(5679-1)(5679+1)-56792 -1
17.;-2023
解:[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷(-2x)
=
.
当x=﹣3,y=﹣2020时,
原式=.
18.(1)5;(2),
解:(1)原式
;
(2)
,
当时,原式.
19.-32
解:原式,
,
原式.
20.(1);(2);(3)
解:(1)∵
∴;
(2)∵.
.
.
(3)∵
∴
又∵,
,
解得: ,
_21?????????è?????(www.21cnjy.com)_
