10.4平移课时训练(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
10.4平移课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
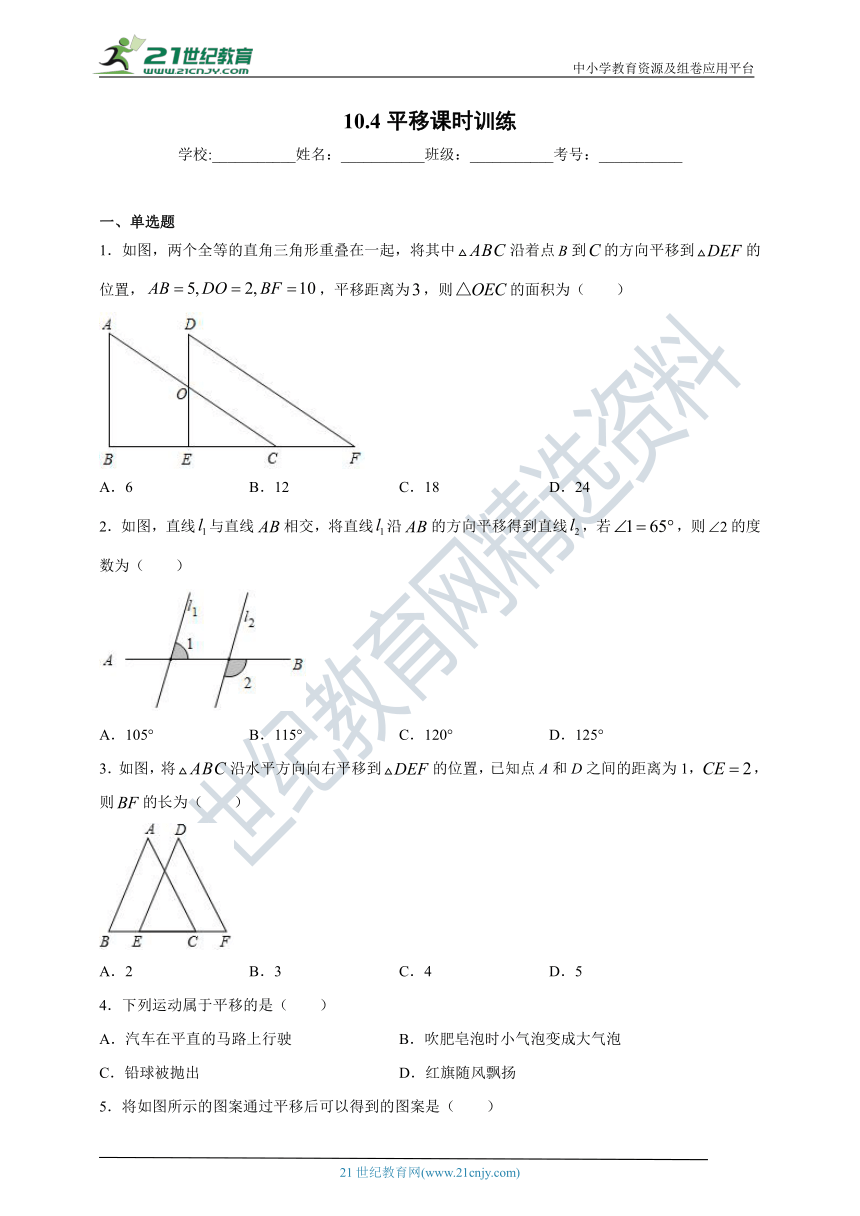
1.如图,两个全等的直角三角形重叠在一起,将其中沿着点到的方向平移到的位置,,平移距离为,则的面积为( )
A.6 B.12 C.18 D.24
2.如图,直线与直线相交,将直线沿的方向平移得到直线,若,则的度数为( )
A.105° B.115° C.120° D.125°
3.如图,将沿水平方向向右平移到的位置,已知点A和D之间的距离为1,,则的长为( )
A.2 B.3 C.4 D.5
4.下列运动属于平移的是( )
A.汽车在平直的马路上行驶 B.吹肥皂泡时小气泡变成大气泡
C.铅球被抛出 D.红旗随风飘扬
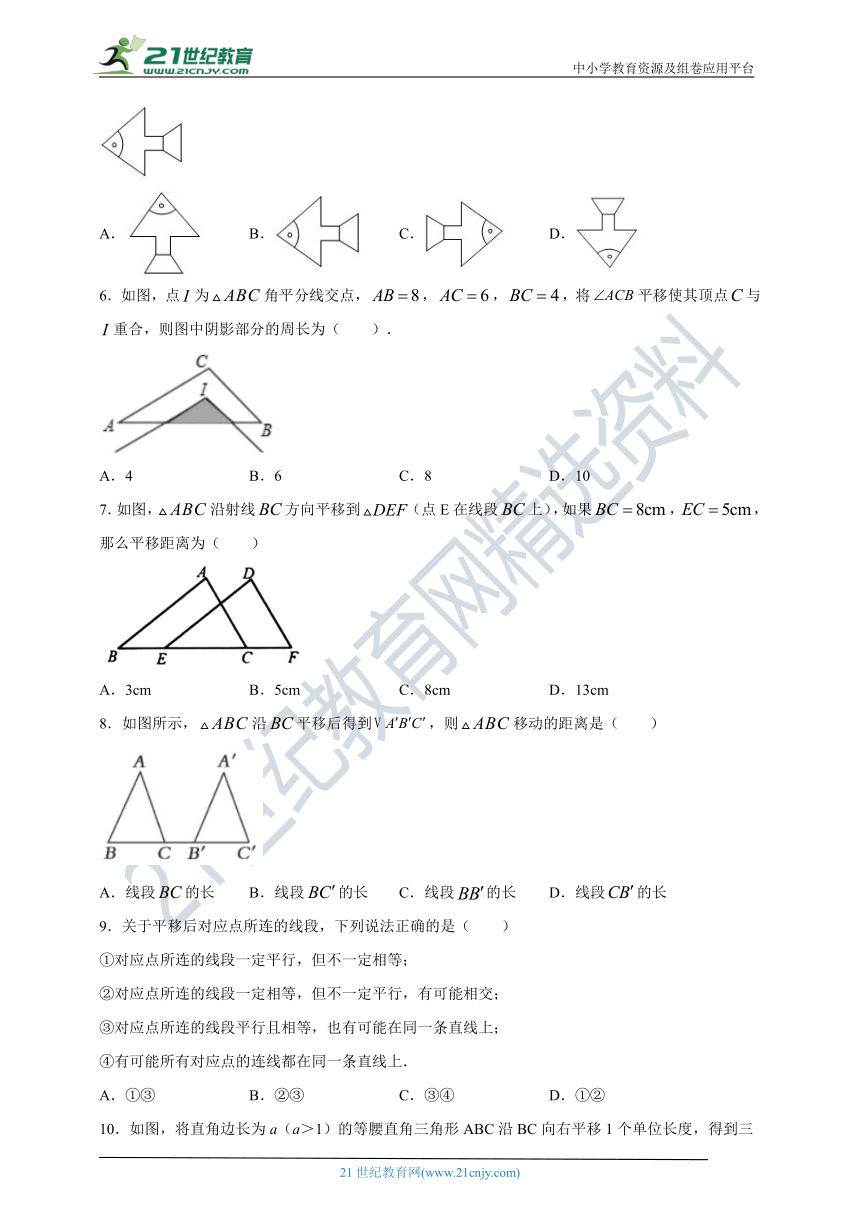
5.将如图所示的图案通过平移后可以得到的图案是( )
A. B. C. D.
6.如图,点为角平分线交点,,,,将平移使其顶点与重合,则图中阴影部分的周长为( ).
A.4 B.6 C.8 D.10
7.如图,沿射线方向平移到(点E在线段上),如果,,那么平移距离为( )
A.3cm B.5cm C.8cm D.13cm
8.如图所示,沿平移后得到,则移动的距离是( )
A.线段的长 B.线段的长 C.线段的长 D.线段的长
9.关于平移后对应点所连的线段,下列说法正确的是( )
①对应点所连的线段一定平行,但不一定相等;
②对应点所连的线段一定相等,但不一定平行,有可能相交;
③对应点所连的线段平行且相等,也有可能在同一条直线上;
④有可能所有对应点的连线都在同一条直线上.
A.①③ B.②③ C.③④ D.①②
10.如图,将直角边长为a(a>1)的等腰直角三角形ABC沿BC向右平移1个单位长度,得到三角形DEF,则图中阴影部分面积为( )
A.a- B.a-1
C.a+1 D.a2-1
二、填空题
11.下列生活中的物体的运动情况可以看成平移的是____.
(1)摆动的钟摆;(2)在笔直的公路上行驶的汽车;(3)随风摆动的旗帜;(4)汽车玻璃上雨刷的运动;(5)从楼顶自由落下的球(球不旋转).
12.如图,将周长为的沿边向右平移个单位,得到则四边形的周长为_____.
13.如图,将沿着射线的方向平移,得到,若,则平移的距离为______.
14.如图,将沿所在的直线平移得到.如果,, 那么____.
15.如图,已知直角三角形,,厘米,厘米,厘米,将沿方向平移1.5厘米,线段在平移过程中所形成图形的面积为__________平方厘米.
16.如图,已知中,、、,将沿直线BC向右平移得到,点A、B、C的对应点分别是、、,连接.如果四边形的周长为19,那么四边形的面积与的面积的比值是________.
三、解答题
17.在图中,利用网格点和三角板画图或计算:
(1)在给定方格纸中画出平移后的,并回答是如何平移的;
(2)图中与A′C′的关系怎样?
(3)记网格的边长为1,则的面积为多少?
18.如图,在每个小正方形边长均为1个单位长度的方格中,有一个且的每个顶点均与小正方形的顶点重合
(1)在方格中,将向下平移5个单位长度得到,请画出.
(2)求平移到的过程中,所扫过的面积.
19.三角形ABC在正方形网格中的位置如图所示,网格中每个小方格的边长为1个单位长度,请根据下列提示作图.
(1)将三角形ABC向上平移3个单位长度,再向右平移2个单位长度得到三角形,画出三角形.
(2)连接,,则三角形的面积为 .
20.如图,点A、B、C的坐标分别为(﹣1,1)、 (3,﹣3)、 (1,﹣2)三角形A1B1C1是由三角形ABC向上平移2个单位长度,再向右平移2个单位长度后得到的,其中点A1、B1、C1分别是点A、B、C的对应点
(1)画出三角形A1B1C1,并写出点A1、B1、C1的坐标;
(2)连接AA1和CC1,若x轴上有一点P(x,0),使得三角形PA1C1的面积等于四边形ACC1A1的面积,求x的值
参考答案
1.A
2.B
3.C
4.A
5.B
6.C
7.A
8.C
9.C
10.A
11.(2)(5)
12.18
13.6
14.
15.6
16.
解:过点A作BC上的高
由平移的性质可得=,且,
∴四边形为梯形
∵四边形的周长为19,
∴+++AB=19
∴+5+6++4=19
∴2=4
∴=2
∴=2
∴=BC+=8
∴四边形的面积与的面积的比为
故答案为:.
17.(1)见解析;(2)AC∥A′C′且AC=A′C′;(3)8
解:(1)如图所示:△ABC向左平移7个单位,向下平移1个单位得到△A′B′C′;
(2)由题意可知:
AC∥A′C′且AC=A′C′;
(3)S△A′B′C′=×4×4=8.
18.(1)见解析;(2)24
解:(1)如图所示:△A1B1C1即为所求.
(2)△ABC所扫过的面积=BB1C1C的面积+△ABC的面积=5×4+4×2÷2=24.
19.(1)见解析;(2)7.5
解:(1)如图,三角形即为所求.
(2)连接,,如图:
∵三角形的面积=×边上的高,
∴
∴三角形的面积为:7.5.
20.(1)见解析,(1,3),(﹣1,﹣1),(3,0);(2)或﹣
解:(1)如图,△A1B1C1为所作,点A1、B1、C1的坐标分别为(1,3),(﹣1,﹣1),(3,0);
(2)四边形ACC1A1的面积=4×5﹣×2×2﹣×2×3﹣×2×2﹣×2×3=10,
?3?|3﹣x|=10,
所以x=
_21?????????è?????(www.21cnjy.com)_
10.4平移课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,两个全等的直角三角形重叠在一起,将其中沿着点到的方向平移到的位置,,平移距离为,则的面积为( )
A.6 B.12 C.18 D.24
2.如图,直线与直线相交,将直线沿的方向平移得到直线,若,则的度数为( )
A.105° B.115° C.120° D.125°
3.如图,将沿水平方向向右平移到的位置,已知点A和D之间的距离为1,,则的长为( )
A.2 B.3 C.4 D.5
4.下列运动属于平移的是( )
A.汽车在平直的马路上行驶 B.吹肥皂泡时小气泡变成大气泡
C.铅球被抛出 D.红旗随风飘扬
5.将如图所示的图案通过平移后可以得到的图案是( )
A. B. C. D.
6.如图,点为角平分线交点,,,,将平移使其顶点与重合,则图中阴影部分的周长为( ).
A.4 B.6 C.8 D.10
7.如图,沿射线方向平移到(点E在线段上),如果,,那么平移距离为( )
A.3cm B.5cm C.8cm D.13cm
8.如图所示,沿平移后得到,则移动的距离是( )
A.线段的长 B.线段的长 C.线段的长 D.线段的长
9.关于平移后对应点所连的线段,下列说法正确的是( )
①对应点所连的线段一定平行,但不一定相等;
②对应点所连的线段一定相等,但不一定平行,有可能相交;
③对应点所连的线段平行且相等,也有可能在同一条直线上;
④有可能所有对应点的连线都在同一条直线上.
A.①③ B.②③ C.③④ D.①②
10.如图,将直角边长为a(a>1)的等腰直角三角形ABC沿BC向右平移1个单位长度,得到三角形DEF,则图中阴影部分面积为( )
A.a- B.a-1
C.a+1 D.a2-1
二、填空题
11.下列生活中的物体的运动情况可以看成平移的是____.
(1)摆动的钟摆;(2)在笔直的公路上行驶的汽车;(3)随风摆动的旗帜;(4)汽车玻璃上雨刷的运动;(5)从楼顶自由落下的球(球不旋转).
12.如图,将周长为的沿边向右平移个单位,得到则四边形的周长为_____.
13.如图,将沿着射线的方向平移,得到,若,则平移的距离为______.
14.如图,将沿所在的直线平移得到.如果,, 那么____.
15.如图,已知直角三角形,,厘米,厘米,厘米,将沿方向平移1.5厘米,线段在平移过程中所形成图形的面积为__________平方厘米.
16.如图,已知中,、、,将沿直线BC向右平移得到,点A、B、C的对应点分别是、、,连接.如果四边形的周长为19,那么四边形的面积与的面积的比值是________.
三、解答题
17.在图中,利用网格点和三角板画图或计算:
(1)在给定方格纸中画出平移后的,并回答是如何平移的;
(2)图中与A′C′的关系怎样?
(3)记网格的边长为1,则的面积为多少?
18.如图,在每个小正方形边长均为1个单位长度的方格中,有一个且的每个顶点均与小正方形的顶点重合
(1)在方格中,将向下平移5个单位长度得到,请画出.
(2)求平移到的过程中,所扫过的面积.
19.三角形ABC在正方形网格中的位置如图所示,网格中每个小方格的边长为1个单位长度,请根据下列提示作图.
(1)将三角形ABC向上平移3个单位长度,再向右平移2个单位长度得到三角形,画出三角形.
(2)连接,,则三角形的面积为 .
20.如图,点A、B、C的坐标分别为(﹣1,1)、 (3,﹣3)、 (1,﹣2)三角形A1B1C1是由三角形ABC向上平移2个单位长度,再向右平移2个单位长度后得到的,其中点A1、B1、C1分别是点A、B、C的对应点
(1)画出三角形A1B1C1,并写出点A1、B1、C1的坐标;
(2)连接AA1和CC1,若x轴上有一点P(x,0),使得三角形PA1C1的面积等于四边形ACC1A1的面积,求x的值
参考答案
1.A
2.B
3.C
4.A
5.B
6.C
7.A
8.C
9.C
10.A
11.(2)(5)
12.18
13.6
14.
15.6
16.
解:过点A作BC上的高
由平移的性质可得=,且,
∴四边形为梯形
∵四边形的周长为19,
∴+++AB=19
∴+5+6++4=19
∴2=4
∴=2
∴=2
∴=BC+=8
∴四边形的面积与的面积的比为
故答案为:.
17.(1)见解析;(2)AC∥A′C′且AC=A′C′;(3)8
解:(1)如图所示:△ABC向左平移7个单位,向下平移1个单位得到△A′B′C′;
(2)由题意可知:
AC∥A′C′且AC=A′C′;
(3)S△A′B′C′=×4×4=8.
18.(1)见解析;(2)24
解:(1)如图所示:△A1B1C1即为所求.
(2)△ABC所扫过的面积=BB1C1C的面积+△ABC的面积=5×4+4×2÷2=24.
19.(1)见解析;(2)7.5
解:(1)如图,三角形即为所求.
(2)连接,,如图:
∵三角形的面积=×边上的高,
∴
∴三角形的面积为:7.5.
20.(1)见解析,(1,3),(﹣1,﹣1),(3,0);(2)或﹣
解:(1)如图,△A1B1C1为所作,点A1、B1、C1的坐标分别为(1,3),(﹣1,﹣1),(3,0);
(2)四边形ACC1A1的面积=4×5﹣×2×2﹣×2×3﹣×2×2﹣×2×3=10,
?3?|3﹣x|=10,
所以x=
_21?????????è?????(www.21cnjy.com)_
