16.2二次根式的运算课时训练(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
16.2二次根式的运算课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列式子中,为最简二次根式的是( )
A. B. C. D.
2.以下各数中与的积是无理数的是 ( )
A. B. C. D.
3.下列二次根式中能与合并的是( )
A. B. C. D.
4.下列二次根式中最简二次根式是( )
A. B. C. D.
5.如果,那么( )
A. B. C. D.
6.化简的结果是( )
A. B. C. D.1
7.实数a,b在数轴上的位置如图,则化简的结果为( )
A. B. C. D.
8.下列二次根式能与合并的是( )
A. B. C. D.
9.已知,,且,则( )
A.2 B.12 C.2或12 D.或
10.若表示a,b两个实数的点在数轴上的位置如图所示,则化简的结果等于( )
A. B. C. D.
二、填空题
11.最简二次根式与是同类最简二次根式,则________.
12.计算:____.
13.已知,则_____,_____.
14.已知,那么的值等于________.
15.已知,当分别取1、2、3、…、2021时,所对应值的总和是_____.
16.若最简二次根式和可以合并,则______.
三、解答题
17.计算:(1) (2)
18.(1)计算
(2)解下列方程:
19.如果的整数部分是a,小数部分是b,求的值.
20.计算:
(1);
(2)已知,求的立方根;
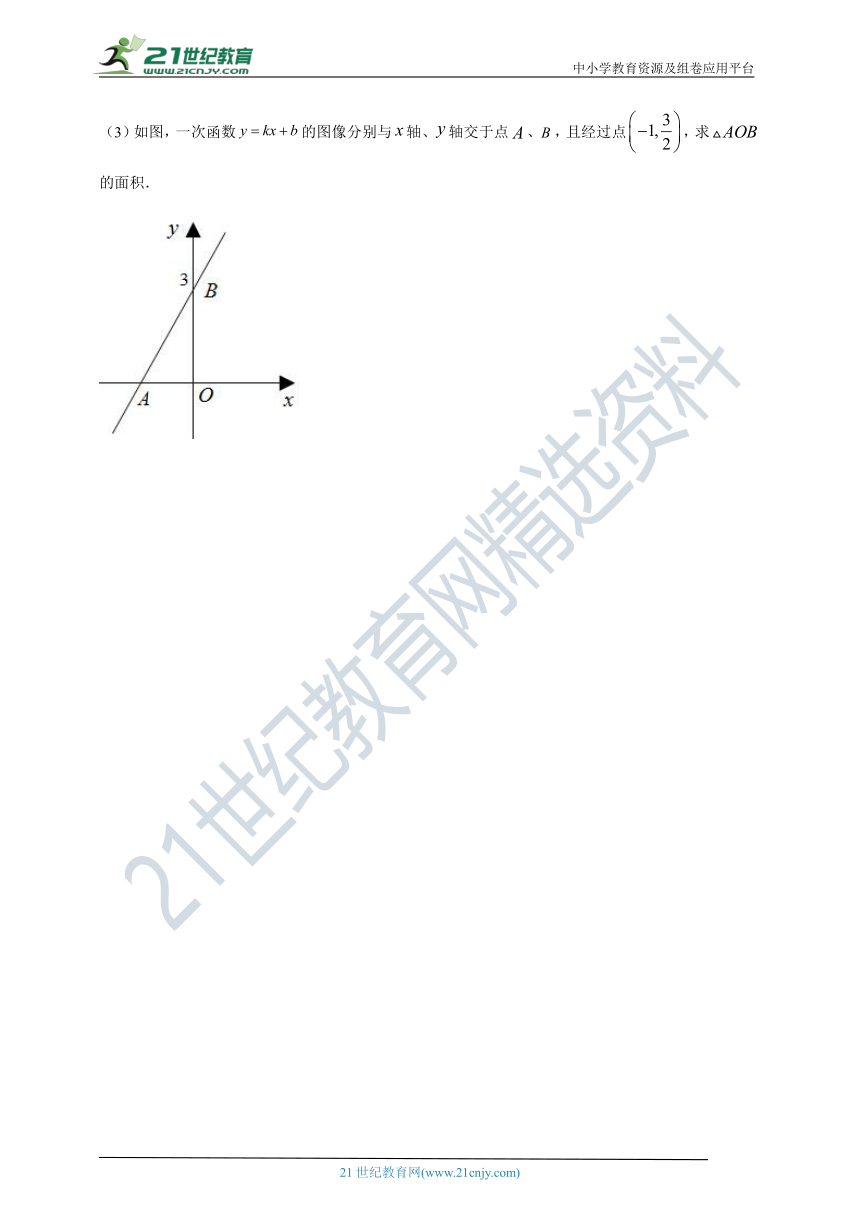
(3)如图,一次函数的图像分别与轴、轴交于点、,且经过点,求的面积.
参考答案
1.B
2.A
3.A
4.A
5.D
6.A
7.B
8.A
9.C
10.C
11.2
12.
13.1 6
14.
15.2033
16.
17.(1)3;(2)
解:(1)
(2)
18.(1);(2)
解:(1)
(2),
由②得:③
把③代入①得:,
∴
把代入③得:
∴原方程组的解为
19..
解:,且,
∴,
,
.
20.(1);(2);(3).
解:(1)原式=;
(2)∵,
∴,
∴,,
∴,
∴,
∴;
∴的立方根为;
(3)由图像可得点B的坐标为,然后把点和点代入一次函数得:
,解得:,
∴一次函数的解析式为,
令y=0时,则有,解得:,
∴OA=2,OB=3,
∴.
_21?????????è?????(www.21cnjy.com)_
16.2二次根式的运算课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列式子中,为最简二次根式的是( )
A. B. C. D.
2.以下各数中与的积是无理数的是 ( )
A. B. C. D.
3.下列二次根式中能与合并的是( )
A. B. C. D.
4.下列二次根式中最简二次根式是( )
A. B. C. D.
5.如果,那么( )
A. B. C. D.
6.化简的结果是( )
A. B. C. D.1
7.实数a,b在数轴上的位置如图,则化简的结果为( )
A. B. C. D.
8.下列二次根式能与合并的是( )
A. B. C. D.
9.已知,,且,则( )
A.2 B.12 C.2或12 D.或
10.若表示a,b两个实数的点在数轴上的位置如图所示,则化简的结果等于( )
A. B. C. D.
二、填空题
11.最简二次根式与是同类最简二次根式,则________.
12.计算:____.
13.已知,则_____,_____.
14.已知,那么的值等于________.
15.已知,当分别取1、2、3、…、2021时,所对应值的总和是_____.
16.若最简二次根式和可以合并,则______.
三、解答题
17.计算:(1) (2)
18.(1)计算
(2)解下列方程:
19.如果的整数部分是a,小数部分是b,求的值.
20.计算:
(1);
(2)已知,求的立方根;
(3)如图,一次函数的图像分别与轴、轴交于点、,且经过点,求的面积.
参考答案
1.B
2.A
3.A
4.A
5.D
6.A
7.B
8.A
9.C
10.C
11.2
12.
13.1 6
14.
15.2033
16.
17.(1)3;(2)
解:(1)
(2)
18.(1);(2)
解:(1)
(2),
由②得:③
把③代入①得:,
∴
把代入③得:
∴原方程组的解为
19..
解:,且,
∴,
,
.
20.(1);(2);(3).
解:(1)原式=;
(2)∵,
∴,
∴,,
∴,
∴,
∴;
∴的立方根为;
(3)由图像可得点B的坐标为,然后把点和点代入一次函数得:
,解得:,
∴一次函数的解析式为,
令y=0时,则有,解得:,
∴OA=2,OB=3,
∴.
_21?????????è?????(www.21cnjy.com)_
