19.2平行四边形课时训练(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
19.2平行四边形课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平行四边形中,,.作于点E,于点F,记的度数为,,.则以下选项错误的是( )
A.
B.的度数为
C.若,则四边形的面积为平行四边形面积的一半
D.若,则平行四边形的周长为
2.平行四边形一边的长是,则这个平行四边形的两条对角线长可以是( )
A.或 B.或 C.或 D.或
3.已知平行四边形的一边长为5,则对角线,的长可取下列数据中的( )
A.2和4 B.3和4 C.4和5 D.5和6
4.已知点,,,.记为内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则所有可能的值为( )
A.6、7 B.7、8 C.6、7、8 D.6、8、9
5.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是( )
A.60 B.30 C.20 D.16
6.在平面直角坐标系中,点A,B,C的坐标分别为,,,当四边形ABCD是平行四边形时,点D的坐标为( )
A. B. C. D.
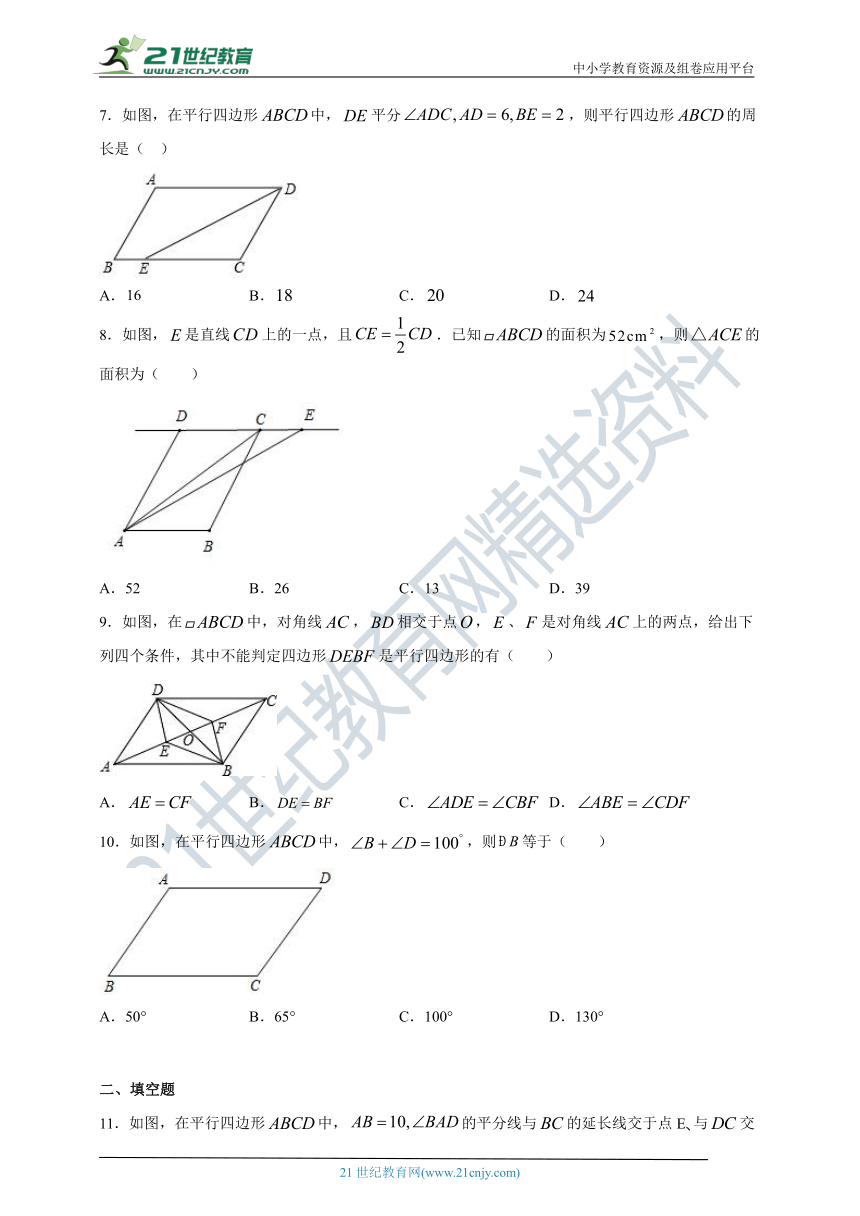
7.如图,在平行四边形中,平分,则平行四边形的周长是( )
A. B. C. D.
8.如图,是直线上的一点,且.已知的面积为,则的面积为( )
A.52 B.26 C.13 D.39
9.如图,在中,对角线,相交于点,、是对角线上的两点,给出下列四个条件,其中不能判定四边形是平行四边形的有( )
A. B. C. D.
10.如图,在平行四边形中,,则等于( )
A.50° B.65° C.100° D.130°
二、填空题
11.如图,在平行四边形中,的平分线与的延长线交于点E?与交于点F,且点F为边的中点,的平分线交于点M,交于点N,连接.若,则的长为_______.
12.点是平行四边形的对称中心,,、分别是边上的点,且;、分别是边上的点,且;若,分别表示和的面积,则,之间的等量关系是__________.
13.如图所示,在平行四边形中,平分交边于点,且,则的长为______.
14.如图,过对角线的交点,交于,交于,若的周长为19,,则四边形的周长为_____.
15.在平面直角坐标系中,的三个顶点的坐标分别为,则其第四个顶点的坐标为______.
16.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠BAD=127°,则∠BCE=____.
三、解答题
17.如图,在中,?分别是和的角平分线,已知.
(1)求线段的长;
(2)延长,交的延长线于点Q.
①请在答卷上补全图形;
②若,求的周长.
18.在中,,点E在边所在的直线上,过点E作交直线于点D,交直线于点F,构造出平行四边形.
(1)若点E在线段上时.
①求证:.
②求证:.
(2)点E在边所在的直线上,若,,请作出简单示意图并直接写出的长度.
19.如图,平行四边形中,分别平分和,交于边上点P,.
(1)求线段的长.
(2)若,求的面积.
20.已知:平行四边形中,点为边的中点,点为边的中点,联结、.
(1)求证:∥;
(2)过点作,垂足为,联结.求证:△是等腰三角形.
参考答案
1.C
2.D
3.D
4.C
5.C
6.A
7.C
8.C
9.B
10.A
11.
12.
13.4
14.14.5
15.
16.37°
17.(1)10;(2)①见解析;②36
解:(1)∵在□ABCD中,AD=5,
∴BC=5,
∵AB∥CD,
∴∠BAP=∠DPA,
∵AP平分∠BAD,
∴∠BAP=∠DAP,
∴∠DAP=∠DPA,
∴DP=AD=5,
同理可得,CP=BC=5,
∴CD=10,
∴AB=10;
(2)①如图所示:
②∵AD∥BQ,
∴∠Q=∠DAP,
又∵∠DAP=∠BAP,
∴∠Q=∠BAP,
∴AB=QB=10,
又∵BP平分∠ABQ,
∴BP⊥AQ,AP=QP,
∴Rt△ABP中,AP==8,
∴AQ=16,
∴△ABQ的周长为:16+10+10=36.
18.(1)①见解析;②见解析;(2)10或6
解:(1)①∵EF∥AC,
∴∠FEB=∠A,
又∵AC=BC,
∴∠B=∠A,
∴∠FEB=∠B,
∴FE=FB;
②∵EF∥AC,DE∥BC,
∴四边形CDEF是平行四边形.
∴CF=DE,
∵EF=BF,
∴DE+EF=CF+BF=BC;
(2)如图,同理可得:BF=EF,
∴DE=BC+BF=BC+EF=8+2=10.
如图,同理可得:BF=EF,
DE=CF=BF-BC=EF-BC=2-8=-6(不合题意).
如图④,
DE=BC-BF=BC-EF=8-2=6.
19.(1)5;(2)6
解:(1)∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵四边形ABCD是平行四边形,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=2.5,
同理:PC=CB=2.5,
即AB=DC=DP+PC=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
在Rt△APB中,AB=5,BP=3,
∴AP==4,
∴△APB的面积=4×3÷2=6.
20.(1)见解析;(2)见解析
解:(1)证明:∵四边形是平行四边形,
∴∥且.
∵点、分别是边、的中点,
∴,.
∴.
又∵∥,
∴四边形是平行四边形
∴∥.
(2)设BH与CN交于点E,
∵AM∥CN,BH⊥AM,
∴BH⊥CN,
∵N是AB的中点,
∴EN是△BAH的中位线,
∴BE=EH,
∴CN是BH的垂直平分线,
∴CH=CB,
∴△BCH是等腰三角形.
_21?????????è?????(www.21cnjy.com)_
19.2平行四边形课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在平行四边形中,,.作于点E,于点F,记的度数为,,.则以下选项错误的是( )
A.
B.的度数为
C.若,则四边形的面积为平行四边形面积的一半
D.若,则平行四边形的周长为
2.平行四边形一边的长是,则这个平行四边形的两条对角线长可以是( )
A.或 B.或 C.或 D.或
3.已知平行四边形的一边长为5,则对角线,的长可取下列数据中的( )
A.2和4 B.3和4 C.4和5 D.5和6
4.已知点,,,.记为内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则所有可能的值为( )
A.6、7 B.7、8 C.6、7、8 D.6、8、9
5.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是( )
A.60 B.30 C.20 D.16
6.在平面直角坐标系中,点A,B,C的坐标分别为,,,当四边形ABCD是平行四边形时,点D的坐标为( )
A. B. C. D.
7.如图,在平行四边形中,平分,则平行四边形的周长是( )
A. B. C. D.
8.如图,是直线上的一点,且.已知的面积为,则的面积为( )
A.52 B.26 C.13 D.39
9.如图,在中,对角线,相交于点,、是对角线上的两点,给出下列四个条件,其中不能判定四边形是平行四边形的有( )
A. B. C. D.
10.如图,在平行四边形中,,则等于( )
A.50° B.65° C.100° D.130°
二、填空题
11.如图,在平行四边形中,的平分线与的延长线交于点E?与交于点F,且点F为边的中点,的平分线交于点M,交于点N,连接.若,则的长为_______.
12.点是平行四边形的对称中心,,、分别是边上的点,且;、分别是边上的点,且;若,分别表示和的面积,则,之间的等量关系是__________.
13.如图所示,在平行四边形中,平分交边于点,且,则的长为______.
14.如图,过对角线的交点,交于,交于,若的周长为19,,则四边形的周长为_____.
15.在平面直角坐标系中,的三个顶点的坐标分别为,则其第四个顶点的坐标为______.
16.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠BAD=127°,则∠BCE=____.
三、解答题
17.如图,在中,?分别是和的角平分线,已知.
(1)求线段的长;
(2)延长,交的延长线于点Q.
①请在答卷上补全图形;
②若,求的周长.
18.在中,,点E在边所在的直线上,过点E作交直线于点D,交直线于点F,构造出平行四边形.
(1)若点E在线段上时.
①求证:.
②求证:.
(2)点E在边所在的直线上,若,,请作出简单示意图并直接写出的长度.
19.如图,平行四边形中,分别平分和,交于边上点P,.
(1)求线段的长.
(2)若,求的面积.
20.已知:平行四边形中,点为边的中点,点为边的中点,联结、.
(1)求证:∥;
(2)过点作,垂足为,联结.求证:△是等腰三角形.
参考答案
1.C
2.D
3.D
4.C
5.C
6.A
7.C
8.C
9.B
10.A
11.
12.
13.4
14.14.5
15.
16.37°
17.(1)10;(2)①见解析;②36
解:(1)∵在□ABCD中,AD=5,
∴BC=5,
∵AB∥CD,
∴∠BAP=∠DPA,
∵AP平分∠BAD,
∴∠BAP=∠DAP,
∴∠DAP=∠DPA,
∴DP=AD=5,
同理可得,CP=BC=5,
∴CD=10,
∴AB=10;
(2)①如图所示:
②∵AD∥BQ,
∴∠Q=∠DAP,
又∵∠DAP=∠BAP,
∴∠Q=∠BAP,
∴AB=QB=10,
又∵BP平分∠ABQ,
∴BP⊥AQ,AP=QP,
∴Rt△ABP中,AP==8,
∴AQ=16,
∴△ABQ的周长为:16+10+10=36.
18.(1)①见解析;②见解析;(2)10或6
解:(1)①∵EF∥AC,
∴∠FEB=∠A,
又∵AC=BC,
∴∠B=∠A,
∴∠FEB=∠B,
∴FE=FB;
②∵EF∥AC,DE∥BC,
∴四边形CDEF是平行四边形.
∴CF=DE,
∵EF=BF,
∴DE+EF=CF+BF=BC;
(2)如图,同理可得:BF=EF,
∴DE=BC+BF=BC+EF=8+2=10.
如图,同理可得:BF=EF,
DE=CF=BF-BC=EF-BC=2-8=-6(不合题意).
如图④,
DE=BC-BF=BC-EF=8-2=6.
19.(1)5;(2)6
解:(1)∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵四边形ABCD是平行四边形,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=2.5,
同理:PC=CB=2.5,
即AB=DC=DP+PC=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA=(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°;
在Rt△APB中,AB=5,BP=3,
∴AP==4,
∴△APB的面积=4×3÷2=6.
20.(1)见解析;(2)见解析
解:(1)证明:∵四边形是平行四边形,
∴∥且.
∵点、分别是边、的中点,
∴,.
∴.
又∵∥,
∴四边形是平行四边形
∴∥.
(2)设BH与CN交于点E,
∵AM∥CN,BH⊥AM,
∴BH⊥CN,
∵N是AB的中点,
∴EN是△BAH的中位线,
∴BE=EH,
∴CN是BH的垂直平分线,
∴CH=CB,
∴△BCH是等腰三角形.
_21?????????è?????(www.21cnjy.com)_
