19.3矩形、菱形、四边形课时训练(含答案)
文档属性
| 名称 | 19.3矩形、菱形、四边形课时训练(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 11:56:42 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
19.3矩形、菱形、四边形课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在Rt△ABC中,∠ACB=90°,AC=,BC=1,CE是斜边AB上的中线,CD是斜边上的高,则DE的长为( )
A. B. C. D.
2.如图,菱形中,分别是的中点,若,则菱形的周长为( )
A.24 B.18 C.12 D.9
3.如图,在和中,,,是的中点,连接,,,若,则的面积为( )
A.12 B.12.5 C.15 D.24
4.顺次连接对角线互相垂直的四边形各边中点,所得到的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.以上都不对
5.如图,在矩形中,点,分别在边,上,且,将矩形沿直线折叠,使点恰好落在边上的点处,则的长为( )
A.9 B.8 C. D.
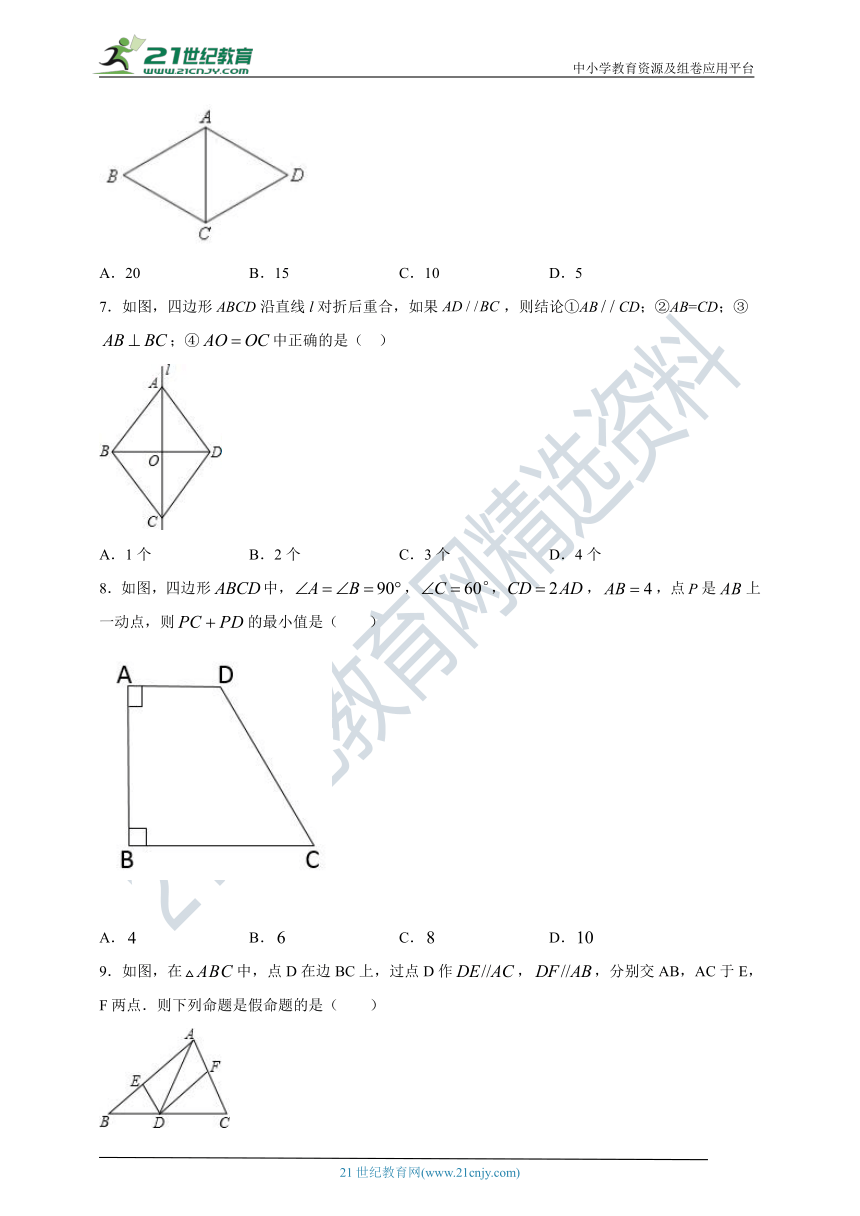
6.如图所示,在菱形中,,,则菱形的周长是( ).
A.20 B.15 C.10 D.5
7.如图,四边形ABCD沿直线l对折后重合,如果,则结论①ABCD;②AB=CD;③;④中正确的是( )
A.1个 B.2个 C.3个 D.4个
8.如图,四边形中,,,,,点是上一动点,则的最小值是( )
A. B. C. D.
9.如图,在中,点D在边BC上,过点D作,,分别交AB,AC于E,F两点.则下列命题是假命题的是( )
A.四边形是平行四边形
B.若,则四边形是矩形
C.若,则四边形是菱形
D.若,则四边形是矩形
10.如图①,在矩形ABCD中,AB>AD,对角线AC,BD相交于点O,动点P由点A出发,沿A→B→C运动.设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示,则AB边的长为( )
A.3 B.4 C.5 D.6
二、填空题
11.已知,在△ABC中,∠BAC=45°,AB=1,AC=,以AC为一边作等腰直角△ACD,使∠CAD=90°,连接BD,则线段BD的长度为________.
12.如图,正方形ABCD的边长为8,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是_____.
13.如图,在矩形纸片中,点是边的中点,沿直线折叠,点落在矩形内部的点处,连接并延长交于点.已知,,则的长为__________.
14.如图,菱形的边长为10,对角线的长为16,点,分别是边,的中点,连接并延长与的延长线相交于点,则的长为________.
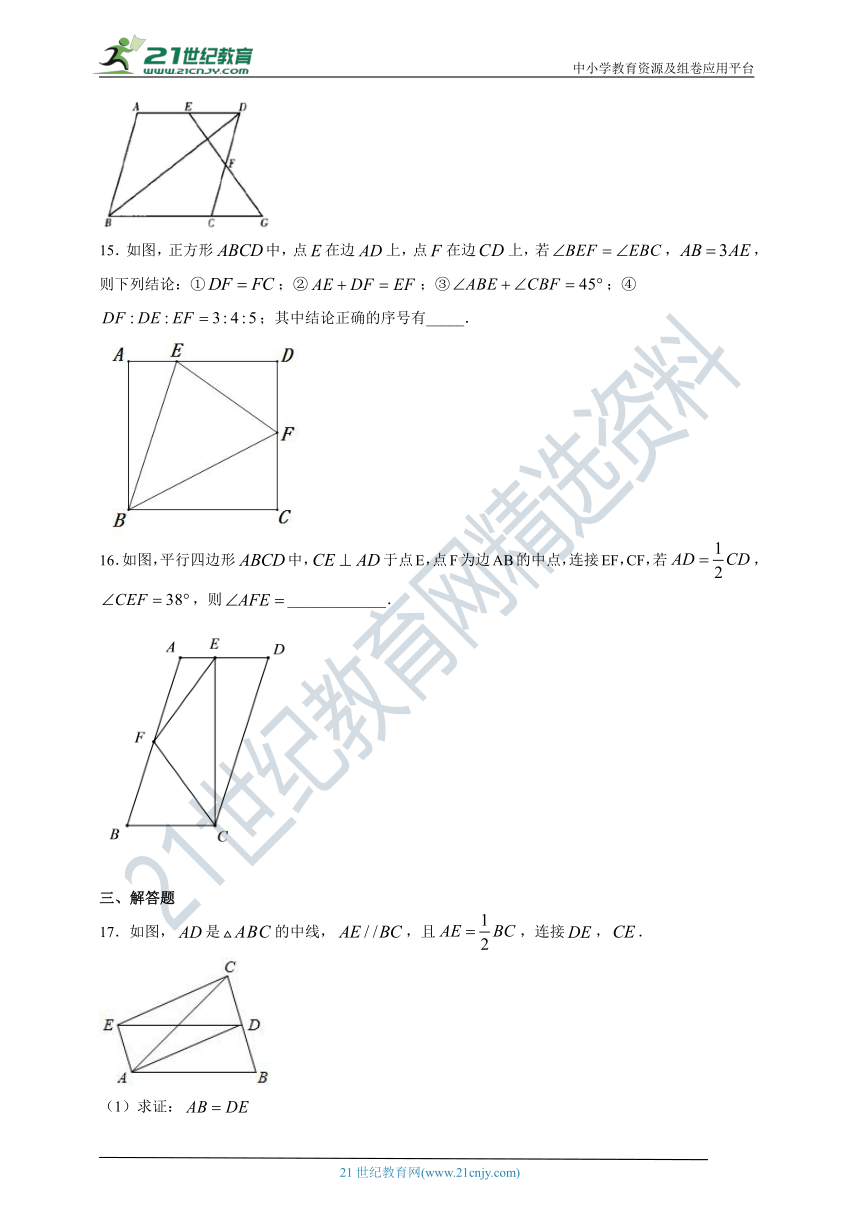
15.如图,正方形中,点在边上,点在边上,若,,则下列结论:①;②;③;④;其中结论正确的序号有_____.
16.如图,平行四边形中,于点E,点F为边AB的中点,连接EF,CF,若,,则_____________.
三、解答题
17.如图,是的中线,,且,连接,.
(1)求证:
(2)当满足什么条件时,四边形是矩形?并说明理由.
18.在正方形中,点、分别在边和上,且满足是等边三角形,连接交于点.
(1)求证:;
(2)若等边边长为,求的长.
19.如图,在中,对角线AC与BD相交于点O,点M,N分别为OB,OD的中点,连接AM并延长至点E,使,连接CE,CN.
(1)求证:;
(2)当AB与AC满足什么数量关系时,四边形MECN是矩形?请说明理由;
(3)连接AN,EN.当满足什么条件时,四边形MECN是正方形?请说明理由.
20.如图所示,沿折叠长方形使点恰好落在边上的点处,已知,.
(1)求的长
(2)求的面积.
参考答案
1.A
2.A
3.A
4.B
5.D
6.A
7.C
8.C
9.C
10.D
11.或
12.4
13.
14.12
15.①②③④
16.24°
17.(1)证明见解析;(2)当满足时,四边形是矩形,证明见解析
(1)是的中线
又
四边形是平行四边形
(2)当满足时,四边形是矩形
,
又
四边形是平行四边形
当时,
四边形是矩形
18.(1)见解析 (2)
(1)证明:正方形,
∴,=90°,.
是等边三角形,
.
.
.
.
(2)由(1)得,CE=CF,AE=AF=2,
垂直平分.
.
,
∵∠ECF=90°,EG=GF,
∴,
.
19.(1)见解析;(2)AC=2AB,理由见解析;(3)当AN=EN且∠ENA=90°时,四边形MECN是正方形.
【详解】
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABM=∠CDN,
∵点M,N分别为OB,OD的中点,
∴
∴BM=DN,
在△ABM和△CDN中,
∴△ABM≌△CDN.
(2)当AC=2AB时,四边形MECN是矩形,
理由如下:∵△ABM≌△CDN,
∴AM=CN,∠AMB=∠CND,
∴∠AMN=∠CNM,
∴AM∥CN,
∵,
∴,
∴四边形EMNC是平行四边形,
∵四边形ABCD是平行四边形,
∴AC=2OA,
∵AC=2AB,
∴AB=OA,
∵M是OB的中点,
∴AM⊥OB,
∴∠NMA=90°,
∴∠NME=90°,
∴平行四边形MECN是矩形.
(3)当AN=EN且∠ENA=90°时,四边形MECN是正方形;
理由如下:连接AN、EN
∵△ABM≌△CDN,
∴AM=CN,∠AMB=∠CND,
∴∠AMN=∠CNM,
∴AM∥CN,
∵,
∴,
∴四边形EMNC是平行四边形,
∵,∠ENA=90°
∴MN=EM,
∴平行四边形EMNC是菱形,
∵AN=EN,AM=EM
∴∠NME=90°,
∴四边形EMNC是正方形.
20.(1)cm;(2)cm2
(1)∵AB=8cm,BC=10cm,
∴DC=8cm,AD=10cm,
又∵将△ADE折叠使点D恰好落在BC边上的点F,
∴AF=AD=10cm,DE=EF,
在Rt△ABF中,AB=8cm,AF=10cm,
∴BF=(cm),
∴FC=10-6=4(cm),
设DE=xcm,则EF=xcm,EC=(8-x)cm,
在Rt△CEF中,EF2=FC2+EC2,即x2=42+(8-x)2,解得x=5,
即DE的长为5cm,
EC=8-x=8-5=3,
即EC的长为3cm;
(2)S△AEF=EF×AF=×5×10=25(cm2).
故△AFE的面积是25cm2.
_21?????????è?????(www.21cnjy.com)_
19.3矩形、菱形、四边形课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在Rt△ABC中,∠ACB=90°,AC=,BC=1,CE是斜边AB上的中线,CD是斜边上的高,则DE的长为( )
A. B. C. D.
2.如图,菱形中,分别是的中点,若,则菱形的周长为( )
A.24 B.18 C.12 D.9
3.如图,在和中,,,是的中点,连接,,,若,则的面积为( )
A.12 B.12.5 C.15 D.24
4.顺次连接对角线互相垂直的四边形各边中点,所得到的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.以上都不对
5.如图,在矩形中,点,分别在边,上,且,将矩形沿直线折叠,使点恰好落在边上的点处,则的长为( )
A.9 B.8 C. D.
6.如图所示,在菱形中,,,则菱形的周长是( ).
A.20 B.15 C.10 D.5
7.如图,四边形ABCD沿直线l对折后重合,如果,则结论①ABCD;②AB=CD;③;④中正确的是( )
A.1个 B.2个 C.3个 D.4个
8.如图,四边形中,,,,,点是上一动点,则的最小值是( )
A. B. C. D.
9.如图,在中,点D在边BC上,过点D作,,分别交AB,AC于E,F两点.则下列命题是假命题的是( )
A.四边形是平行四边形
B.若,则四边形是矩形
C.若,则四边形是菱形
D.若,则四边形是矩形
10.如图①,在矩形ABCD中,AB>AD,对角线AC,BD相交于点O,动点P由点A出发,沿A→B→C运动.设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示,则AB边的长为( )
A.3 B.4 C.5 D.6
二、填空题
11.已知,在△ABC中,∠BAC=45°,AB=1,AC=,以AC为一边作等腰直角△ACD,使∠CAD=90°,连接BD,则线段BD的长度为________.
12.如图,正方形ABCD的边长为8,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是_____.
13.如图,在矩形纸片中,点是边的中点,沿直线折叠,点落在矩形内部的点处,连接并延长交于点.已知,,则的长为__________.
14.如图,菱形的边长为10,对角线的长为16,点,分别是边,的中点,连接并延长与的延长线相交于点,则的长为________.
15.如图,正方形中,点在边上,点在边上,若,,则下列结论:①;②;③;④;其中结论正确的序号有_____.
16.如图,平行四边形中,于点E,点F为边AB的中点,连接EF,CF,若,,则_____________.
三、解答题
17.如图,是的中线,,且,连接,.
(1)求证:
(2)当满足什么条件时,四边形是矩形?并说明理由.
18.在正方形中,点、分别在边和上,且满足是等边三角形,连接交于点.
(1)求证:;
(2)若等边边长为,求的长.
19.如图,在中,对角线AC与BD相交于点O,点M,N分别为OB,OD的中点,连接AM并延长至点E,使,连接CE,CN.
(1)求证:;
(2)当AB与AC满足什么数量关系时,四边形MECN是矩形?请说明理由;
(3)连接AN,EN.当满足什么条件时,四边形MECN是正方形?请说明理由.
20.如图所示,沿折叠长方形使点恰好落在边上的点处,已知,.
(1)求的长
(2)求的面积.
参考答案
1.A
2.A
3.A
4.B
5.D
6.A
7.C
8.C
9.C
10.D
11.或
12.4
13.
14.12
15.①②③④
16.24°
17.(1)证明见解析;(2)当满足时,四边形是矩形,证明见解析
(1)是的中线
又
四边形是平行四边形
(2)当满足时,四边形是矩形
,
又
四边形是平行四边形
当时,
四边形是矩形
18.(1)见解析 (2)
(1)证明:正方形,
∴,=90°,.
是等边三角形,
.
.
.
.
(2)由(1)得,CE=CF,AE=AF=2,
垂直平分.
.
,
∵∠ECF=90°,EG=GF,
∴,
.
19.(1)见解析;(2)AC=2AB,理由见解析;(3)当AN=EN且∠ENA=90°时,四边形MECN是正方形.
【详解】
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABM=∠CDN,
∵点M,N分别为OB,OD的中点,
∴
∴BM=DN,
在△ABM和△CDN中,
∴△ABM≌△CDN.
(2)当AC=2AB时,四边形MECN是矩形,
理由如下:∵△ABM≌△CDN,
∴AM=CN,∠AMB=∠CND,
∴∠AMN=∠CNM,
∴AM∥CN,
∵,
∴,
∴四边形EMNC是平行四边形,
∵四边形ABCD是平行四边形,
∴AC=2OA,
∵AC=2AB,
∴AB=OA,
∵M是OB的中点,
∴AM⊥OB,
∴∠NMA=90°,
∴∠NME=90°,
∴平行四边形MECN是矩形.
(3)当AN=EN且∠ENA=90°时,四边形MECN是正方形;
理由如下:连接AN、EN
∵△ABM≌△CDN,
∴AM=CN,∠AMB=∠CND,
∴∠AMN=∠CNM,
∴AM∥CN,
∵,
∴,
∴四边形EMNC是平行四边形,
∵,∠ENA=90°
∴MN=EM,
∴平行四边形EMNC是菱形,
∵AN=EN,AM=EM
∴∠NME=90°,
∴四边形EMNC是正方形.
20.(1)cm;(2)cm2
(1)∵AB=8cm,BC=10cm,
∴DC=8cm,AD=10cm,
又∵将△ADE折叠使点D恰好落在BC边上的点F,
∴AF=AD=10cm,DE=EF,
在Rt△ABF中,AB=8cm,AF=10cm,
∴BF=(cm),
∴FC=10-6=4(cm),
设DE=xcm,则EF=xcm,EC=(8-x)cm,
在Rt△CEF中,EF2=FC2+EC2,即x2=42+(8-x)2,解得x=5,
即DE的长为5cm,
EC=8-x=8-5=3,
即EC的长为3cm;
(2)S△AEF=EF×AF=×5×10=25(cm2).
故△AFE的面积是25cm2.
_21?????????è?????(www.21cnjy.com)_
