贵州省湄潭中学11-12学年高二上学期期末试题数学
文档属性
| 名称 | 贵州省湄潭中学11-12学年高二上学期期末试题数学 |
|
|
| 格式 | zip | ||
| 文件大小 | 61.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-17 00:00:00 | ||
图片预览




文档简介
湄潭中学2011—2012学年第一学期学期测试
高二年级数学科试卷
一 选择题(每题5分共60分)
1.直线在轴上的截距为a,在轴上的截距为b,则 ( )
A a=2 b=5 B a=2 b= -5 C a= -2 b= 5 D a= -2 b= -5
2.若以点, ,为顶点的 是直角三角形,则 值为 ( )
A. 1 B.2 C.3 D.1或3
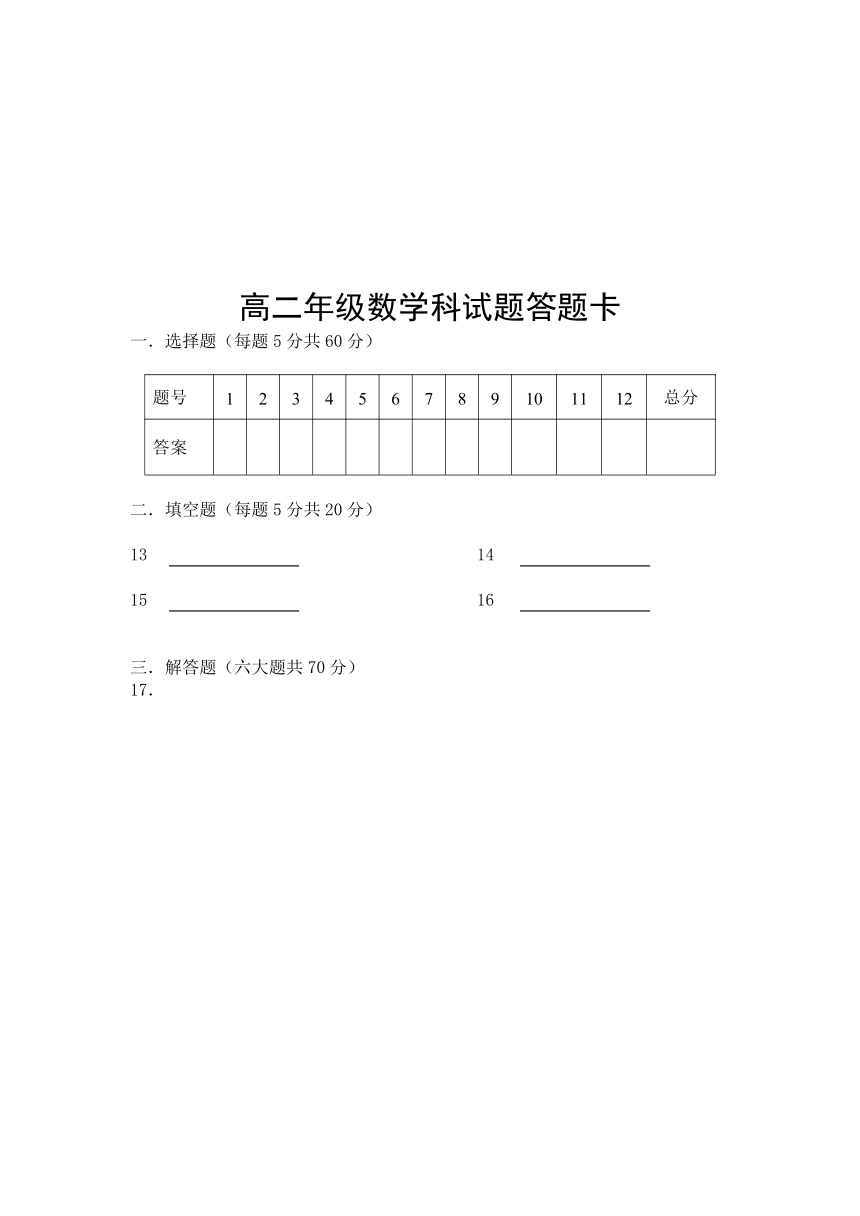
3.下图是容量为200的样本的频率分布直方图,那么样本数据落在内的频率、频数分别为 ( )
A.0.32,64 B.0.32,62 C.0.36,64 D. 0.36,72
4.先后抛掷两颗骰子,设出现的点数之和是12,11,10的频率分别为P1,P2,P3 则 ( )
A.P1〈 P2〈P3 B. P1= P2〈P3 C. P1〈 P2=P3 D. P3= P2〈P1
5.下面的程序框图所表示的算法功能是 ( )
A.计算的值 B.计算的值
C计算的值D计算的值
(第三题)
6.已知直线:与曲线C:的公共点不多于一个,则实数的取值范围为 ( )
A. B. C. D.
7.如图,正方休ABCD—A1B1C1D1中,E、F为AA1、AB的中点,则图中与EF是异面直线的直线有( )条
A.8 B . 9 C .10 D .11
8.过点P(4,-1)且与直线平行的直线为 ( )
A. B.
C. D.
9.直线与圆的位置关系是 ( )
A.相切 B .相交 C.相离 D. 无法判定
10.能使平面∥平面的一个条件是 ( )
A.存在一条直线,∥,∥
B.存在一条直线,,∥
C 存在两条直线,,,,∥,∥
D.存在两条异面直线,,,,∥,∥
11.二面角大小为600, 、是异面直线,,,则, 所成的角是 ( )
A.300 B .600 C. 900 D . 1200
12.圆与圆相交于A、B两点,则以AB为直径的圆的方程是 ( )
A. B.
C. D .
二:填空题(每题5分共20分)
13.如图是一个简单几何体的三视图,其中主视图和左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则该几何体的表面积是____.
14.半径为a的球放置在墙角,同时与两墙面相切,则球心到墙角顶点的距离是____.
15.已知是上的一个随机数,则使满足的概率为____.
16.一企业生产不同型号的水泥19500袋,它们来自甲、乙、丙三条不同的生产线,为了检查这批水泥的质量,决定采用分层抽样的方法进行检测。已知甲、乙、丙生产线抽取的个数组成一个等差数列,则乙生产线生产了____袋水泥。
三:解答题
17.(10分)已知,A(-1,4),B(-2,-1),C(4,3),M是BC的中点。
(1)求线段BC中垂线的方程;
(2)求外接圆的方程。
18.(12分)如图,在底面是直角梯形的四棱锥中,,面,,。
(1)求证:面;
(2)求点C到平面的距离。
19.(12分)对甲、乙两位同学的学习成绩进行抽样分析,各抽5门课得到的观测值如下:
甲 60 80 70 90 70
乙 80 60 70 85 75
(1)计算甲、乙两同学学习成绩平均数和标准差;
(2)比较两人的成绩,分析谁的各门功课发展较平衡。
20.(12分)一只口袋内装有大小相同的5只球,其中3只白球,2只黑球,现从袋中每次任取一球,每次取出不放回,连续取两次,问:
(1)取出的两只球都是白球的概率是多少;
(2)取出的两球至少有一个白球的概率是多少。
21.(12分)已知圆C: 与
直线:,
(1)证明:对,与圆C恒交于两点;
(2)求直线被圆C截得的线段最短长度,并求此时的值。
22.(12分)设计一个程序框图求的值,并写出程序。
高二年级数学科试题答题卡
选择题(每题5分共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 总分
答案
二.填空题(每题5分共20分)
13 14
15 16
三.解答题(六大题共70分)
17.
18.
19.
20.
21.
22.
高二年级数学科试题参考答案
一.选择题(每题5分共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 总分
答案 B D D A C B C C A D B A
二.填空题(每题5分共20分)
13. 12 14. 15. 16. 6500
三.解答题(六大题共70分)
17.解:(1)由B(-2,-1),C(4,3),得
BC中点M的坐标为(1,1)………………………………………………1分
…………………………………………2分
故BC中垂线的斜率为…………………………………………………3分
于是BC中垂线方程为,即……………5分
(2)设所求圆方程为,
将A(-1,4),B(-2,-1),C(4,3)得:……………………………6分
…………………………………………8分
解得D=-2 ,E=-2 ,F=-11
故所求圆方程为 …………………………10分
18.证明:(1)
由,,而
,而
(2)方法不一,答案为,设所求距离为.
===
由题易得,,于是得
=
由 得
19.解:由表得
甲平均成绩好,乙的各门功课发展更平衡
20.(1) (2)
21.(1)提示;直线过定点(-2,3)(略)
(2)线段最短为10,此时
22.
开始
S=0,n=1,i=1
i>50
S=S+1/n
n=n+2
i=i+1
输出S
结束
Y
N
样本数据
O
y
O
2
6
10
14
182
222
0.02
0.03
0.08
频率/组距
F
D1
A
B
D
C
A1
B1
C1
E
主视图
左视图
俯视图
B
C
D
A
S
B
C
D
A
S
开始
i=1
S=0
S=S+i3
i=i+1
i>50
输出S
结束
是
否
i=1
S=0
DO
S=S+i
i=i+1
LOOP UNTIL i>50
PRINT S
END
高二年级数学科试卷
一 选择题(每题5分共60分)
1.直线在轴上的截距为a,在轴上的截距为b,则 ( )
A a=2 b=5 B a=2 b= -5 C a= -2 b= 5 D a= -2 b= -5
2.若以点, ,为顶点的 是直角三角形,则 值为 ( )
A. 1 B.2 C.3 D.1或3
3.下图是容量为200的样本的频率分布直方图,那么样本数据落在内的频率、频数分别为 ( )
A.0.32,64 B.0.32,62 C.0.36,64 D. 0.36,72
4.先后抛掷两颗骰子,设出现的点数之和是12,11,10的频率分别为P1,P2,P3 则 ( )
A.P1〈 P2〈P3 B. P1= P2〈P3 C. P1〈 P2=P3 D. P3= P2〈P1
5.下面的程序框图所表示的算法功能是 ( )
A.计算的值 B.计算的值
C计算的值D计算的值
(第三题)
6.已知直线:与曲线C:的公共点不多于一个,则实数的取值范围为 ( )
A. B. C. D.
7.如图,正方休ABCD—A1B1C1D1中,E、F为AA1、AB的中点,则图中与EF是异面直线的直线有( )条
A.8 B . 9 C .10 D .11
8.过点P(4,-1)且与直线平行的直线为 ( )
A. B.
C. D.
9.直线与圆的位置关系是 ( )
A.相切 B .相交 C.相离 D. 无法判定
10.能使平面∥平面的一个条件是 ( )
A.存在一条直线,∥,∥
B.存在一条直线,,∥
C 存在两条直线,,,,∥,∥
D.存在两条异面直线,,,,∥,∥
11.二面角大小为600, 、是异面直线,,,则, 所成的角是 ( )
A.300 B .600 C. 900 D . 1200
12.圆与圆相交于A、B两点,则以AB为直径的圆的方程是 ( )
A. B.
C. D .
二:填空题(每题5分共20分)
13.如图是一个简单几何体的三视图,其中主视图和左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则该几何体的表面积是____.
14.半径为a的球放置在墙角,同时与两墙面相切,则球心到墙角顶点的距离是____.
15.已知是上的一个随机数,则使满足的概率为____.
16.一企业生产不同型号的水泥19500袋,它们来自甲、乙、丙三条不同的生产线,为了检查这批水泥的质量,决定采用分层抽样的方法进行检测。已知甲、乙、丙生产线抽取的个数组成一个等差数列,则乙生产线生产了____袋水泥。
三:解答题
17.(10分)已知,A(-1,4),B(-2,-1),C(4,3),M是BC的中点。
(1)求线段BC中垂线的方程;
(2)求外接圆的方程。
18.(12分)如图,在底面是直角梯形的四棱锥中,,面,,。
(1)求证:面;
(2)求点C到平面的距离。
19.(12分)对甲、乙两位同学的学习成绩进行抽样分析,各抽5门课得到的观测值如下:
甲 60 80 70 90 70
乙 80 60 70 85 75
(1)计算甲、乙两同学学习成绩平均数和标准差;
(2)比较两人的成绩,分析谁的各门功课发展较平衡。
20.(12分)一只口袋内装有大小相同的5只球,其中3只白球,2只黑球,现从袋中每次任取一球,每次取出不放回,连续取两次,问:
(1)取出的两只球都是白球的概率是多少;
(2)取出的两球至少有一个白球的概率是多少。
21.(12分)已知圆C: 与
直线:,
(1)证明:对,与圆C恒交于两点;
(2)求直线被圆C截得的线段最短长度,并求此时的值。
22.(12分)设计一个程序框图求的值,并写出程序。
高二年级数学科试题答题卡
选择题(每题5分共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 总分
答案
二.填空题(每题5分共20分)
13 14
15 16
三.解答题(六大题共70分)
17.
18.
19.
20.
21.
22.
高二年级数学科试题参考答案
一.选择题(每题5分共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12 总分
答案 B D D A C B C C A D B A
二.填空题(每题5分共20分)
13. 12 14. 15. 16. 6500
三.解答题(六大题共70分)
17.解:(1)由B(-2,-1),C(4,3),得
BC中点M的坐标为(1,1)………………………………………………1分
…………………………………………2分
故BC中垂线的斜率为…………………………………………………3分
于是BC中垂线方程为,即……………5分
(2)设所求圆方程为,
将A(-1,4),B(-2,-1),C(4,3)得:……………………………6分
…………………………………………8分
解得D=-2 ,E=-2 ,F=-11
故所求圆方程为 …………………………10分
18.证明:(1)
由,,而
,而
(2)方法不一,答案为,设所求距离为.
===
由题易得,,于是得
=
由 得
19.解:由表得
甲平均成绩好,乙的各门功课发展更平衡
20.(1) (2)
21.(1)提示;直线过定点(-2,3)(略)
(2)线段最短为10,此时
22.
开始
S=0,n=1,i=1
i>50
S=S+1/n
n=n+2
i=i+1
输出S
结束
Y
N
样本数据
O
y
O
2
6
10
14
182
222
0.02
0.03
0.08
频率/组距
F
D1
A
B
D
C
A1
B1
C1
E
主视图
左视图
俯视图
B
C
D
A
S
B
C
D
A
S
开始
i=1
S=0
S=S+i3
i=i+1
i>50
输出S
结束
是
否
i=1
S=0
DO
S=S+i
i=i+1
LOOP UNTIL i>50
PRINT S
END
同课章节目录
