2020-2021学年苏科版数学七年级下册7.1 探索直线平行的条件 提优训练(Word版 含答案)
文档属性
| 名称 | 2020-2021学年苏科版数学七年级下册7.1 探索直线平行的条件 提优训练(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 753.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 20:40:50 | ||
图片预览


文档简介
7.1 探索直线平行的条件 提优训练
一、单选题
1.(2020·甘肃天水市·七年级期末)如图的四个图中,∠1与∠2是同位角的有( )
A.②③ B.①②③ C.① D.①②④
2.(2021·四川眉山市·七年级期末)如图,直线a,b,c被射线l和m所截,则下列关系正确的是( )
A.∠1与∠2是对顶角 B.∠1与∠3是同旁内角
C.∠3与∠4是同位角 D.∠2与∠3是内错角
3.(2021·陕西宝鸡市·七年级期末)下列说法中正确的个数为( )
①不相交的两条直线叫做平行线;②平面内,过一点有且只有一条直线与已知直线垂直;
③平行于同一条直线的两条直线互相平行;④在同一平面内,两条直线不是平行就是相交.
A.1个 B.2个 C.3个 D.4个
4.(2021·四川成都市·八年级期末)如图,在下列条件中,能判断AB∥CD的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.∠BAD+∠ADC=180° D.∠3=∠4
5.(2021·渝中区·重庆巴蜀中学七年级开学考试)如图,在下列给出的条件中,可以判定的有( )
①;②;③;④;⑤.
A.①②③ B.①②④ C.①④⑤ D.②③⑤
6.(2021·全国七年级专题练习)如图,下列条件中,不能判断直线a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
7.(2020·山东青岛市·七年级期中)如图,下列不能判定DF∥AC的条件是( )
A.∠A=∠BDF B.∠2=∠4 C.∠1=∠3 D.∠A+∠ADF=180°
8.(2020·陕西宝鸡市·七年级期末)下列条件能判定直线l1∥l2的是( )
A.∠2=∠3 B.∠1=∠3 C.∠4+∠5=180° D.∠2=∠4
9.(2020·广东清远市·八年级期末)如图所示,下列推理及括号中所注明的推理依据错误的是( )
A.∵∠1=∠3,∴AB∥CD(内错角相等,两直线平行)
B.∵AB∥CD,∴∠1=∠3(两直线平行,内错角相等)
C.∵AD∥BC,∴∠BAD+∠ABC=180°(两直线平行,同旁内角互补)
D.∵∠DAM=∠CBM,∴AB∥CD(两直线平行,同位角相等)
10.(2020·山东菏泽市·七年级期末)如图,,C点在EF上,,BC平分,且.下列结论:
①AC平分;②;③;④.其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2020·浙江七年级期末)如图,点B,C,E在同一条直线上,请你写出一个能使成立的条件:_______.(只写一个即可,不添加任何字母或数字)
12.(2019·浙江杭州市·七年级开学考试)如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是___.
13.(2020·上海同济大学实验学校)如图,共有_____对同位角,有_____对内错角,有_____对同旁内角.
14.(2020·上海同济大学实验学校)如图,∠1与∠2是直线_____和_____被直线_____所截的一对_____角.
15.(2020·浙江七年级期末)将一块三角板(,)按如图方式放置,使,两点分别放在直线,上,对于给出的四个条件,①,;②;③,④;⑤.能判断直线的有________(填序号).
16.(2020·甘肃白银市·平川区四中七年级期末)如图,下列能判定的条件有_______个.
①;②;③;④.
17.(2019·河南洛阳市·洛阳地矿双语学校七年级月考)如图,现给出下列条件:①,②,③,④,⑤.其中能够得到AB//CD的条件是_______.(只填序号)
18.(2020·江苏扬州市·七年级期中)一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),当∠BAD=_____时,CD∥AB.
19.(2020·安徽蚌埠市·七年级期末)规律探究:同一平面内有直线、、,,,若,,,,,按此规律,与的位置关系是______.
20.(2020·福建泉州市·泉州五中七年级月考)在同一平面内有2019条直线,,如果,,那么①的位置关系是__________②的位置关系是_______________
三、解答题
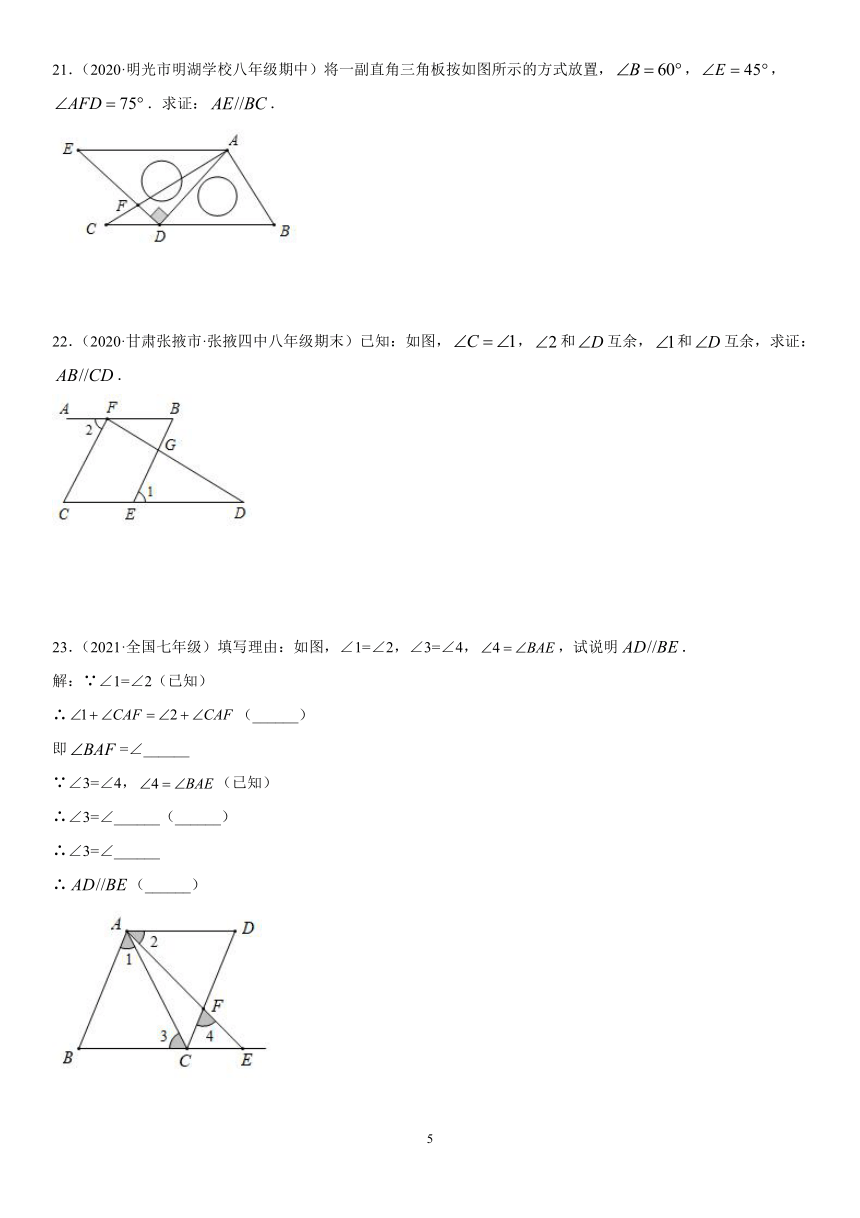
21.(2020·明光市明湖学校八年级期中)将一副直角三角板按如图所示的方式放置,,,.求证:.
22.(2020·甘肃张掖市·张掖四中八年级期末)已知:如图,,和互余,和互余,求证:.
23.(2021·全国七年级)填写理由:如图,∠1=∠2,∠3=∠4,,试说明.
解:∵∠1=∠2(已知)
∴(______)
即=∠______
∵∠3=∠4,(已知)
∴∠3=∠______(______)
∴∠3=∠______
∴(______)
24.(2020·甘肃兰州市·七年级期末)看图填空,并在括号内注明说理依据.
如图,已知,,,,与平行吗?与平行吗?
解:因为,(已知),
所以.
所以 ( ).
又因为 (已知),
所以.( )
所以.
同理可得, .
所以( ).
所以 (同位角相等,两直线平行).
25.(2019·河南平顶山市·八年级期末)如图,在中,平分交于点,点是边上一点,连接,若,求证:.
26.(2019·全国七年级单元测试)如图,∠BEC=95°,∠ABE=120°,∠DCE=35°,则AB与CD平行吗?请说明理由.
27.(2021·全国七年级专题练习)如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG相交于点H,∠C=∠EFG,∠BFG=∠AEM,求证:AB∥CD.(完成下列填空)
证明:∵∠BFG=∠AEM(已知)
且∠AEM=∠BEC( )
∴∠BEC=∠BFG(等量代换)
∴MC∥ ( )
∴∠C=∠FGD( )
∵∠C=∠EFG(已知)
∴∠ =∠EFG,(等量代换)
∴AB∥CD( )
28.(2020·绍兴市文澜中学七年级期中)如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
29.(2019·广东韶关市·七年级期末)将一副三角板中的两个直角顶点叠放在一起(如图①),其中,,.
(1)猜想与的数量关系,并说明理由;
(2)若,求的度数;
(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.
30.(2018·贵州遵义市·达兴中学七年级期中)如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
参考答案
1.D 2.C 3.C 4.C 5.D 6.B 7.B 8.B 9.D 10.D
11.∠1=∠2(答案不唯一) 12.同位角相等,两直线平行 13.20 12 12
14.a b c 内错 15.①⑤ 16.1 17.①②⑤ 18.150°或30°.
19.互相垂直. 20.平行 垂直
21.见解析
【详解】
解:由直角三角板的性质可得:
∠C=30°,
∵∠AFD=∠C+∠CDF=75°,
∴∠CDF=45°,
∴∠CDF=∠E,
∴AE∥BC.
22.证明见详解
【详解】
解:证明:∵∠1和∠D互余,∠2和∠D互余,
∴∠1=∠2,
∵∠C=∠1,
∴∠C=∠2,
∴AB∥CD.
23.见解析
【详解】
∵∠1=∠2(已知)
∴(等式的性质)
即=∠ DAC
∵∠3=∠4,(已知)
∴∠3=∠BAE(等量代换)
∴∠3=∠DAC
∴(内错角相等,两直线平行)
24.AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF..
【详解】
解:因为∠1=35°,∠2=35°(已知),
所以∠1=∠2.
所以AC∥BD(同位角相等,两直线平行).
又因为AC⊥AE(已知),
所以∠EAC=90°.(垂直的定义)
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=125°.
所以∠EAB=∠FBG(等量代换).
所以AE∥BF(同位角相等,两直线平行).
故答案为:AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.
25.证明见解析
【详解】
证明:在中,
,
平分
,
26.平行,理由见解析.
【详解】
解:AB∥CD,理由如下:
如图所示,延长BE,交CD于点F,
因为∠BEC=95°,
所以∠CEF=180°-95°=85°.
又因为∠DCE=35°,
所以∠BFC=180°-∠DCE-∠CEF=180°-35°-85°=60°.
因为∠ABE=120°(已知),
所以∠ABE+∠BFC=180°,
所以AB∥CD(同旁内角互补,两直线平行).
27.对顶角相等;GF;同位角相等,两直线平行;FGD;内错角相等,两直线平行
【详解】
证明:∵∠BFG=∠AEM(已知)
且∠AEM=∠BEC(对顶角相等)
∴∠BEC=∠BFG(等量代换)
∴MC∥GF(同位角相等,两直线平行)
∴∠C=∠FGD( 两直线平行,同位角相等)
∵∠C=∠EFG(已知)
∴∠FGD=∠EFG,(等量代换)
∴AB∥CD(内错角相等,两直线平行).
故答案是:对顶角相等;GF;同位角相等,两直线平行;FGD;内错角相等,两直线平行.
28.(1)见解析;(2) 见解析.
【详解】
证明:(1)∵∠1+∠AFE=180°,∠1+∠BCF=180°,
∴∠AFE=∠BCF,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
29.(1),理由详见解析;(2)135°;(3)等于或时,.
【详解】
解:(1),理由如下:
,
;
(2)如图①,设,则,
由(1)可得,
,
,
;
(3)分两种情况:
①如图1所示,当时,,
又,
;
②如图2所示,当时,,
又,
.
综上所述,等于或时,.
30.见解析
详解:(1)∵∠1=∠3,∠2=∠4,∴∠1+∠3+∠2+∠4=2(∠1+∠2),
∵∠1+∠2=90°,∴∠1+∠3+∠2+∠4=180°;
∵∠D+∠B+∠1+∠3+∠2+∠4=360°,∴∠D+∠B=180°,
∴DE∥BC.
(2)成立.
如图2,连接EC;
∵∠1=∠3,∠2=∠4,且∠1+∠2=90°,∴∠3+∠4=∠1+∠2=90°;
∵∠EAC=90°,∴∠AEC+∠ACE=180°-90°=90°,
∴∠AEC+∠ACE+∠3+∠4=180°,
∴DE∥BC,
即(1)中的结论仍成立.
一、单选题
1.(2020·甘肃天水市·七年级期末)如图的四个图中,∠1与∠2是同位角的有( )
A.②③ B.①②③ C.① D.①②④
2.(2021·四川眉山市·七年级期末)如图,直线a,b,c被射线l和m所截,则下列关系正确的是( )
A.∠1与∠2是对顶角 B.∠1与∠3是同旁内角
C.∠3与∠4是同位角 D.∠2与∠3是内错角
3.(2021·陕西宝鸡市·七年级期末)下列说法中正确的个数为( )
①不相交的两条直线叫做平行线;②平面内,过一点有且只有一条直线与已知直线垂直;
③平行于同一条直线的两条直线互相平行;④在同一平面内,两条直线不是平行就是相交.
A.1个 B.2个 C.3个 D.4个
4.(2021·四川成都市·八年级期末)如图,在下列条件中,能判断AB∥CD的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.∠BAD+∠ADC=180° D.∠3=∠4
5.(2021·渝中区·重庆巴蜀中学七年级开学考试)如图,在下列给出的条件中,可以判定的有( )
①;②;③;④;⑤.
A.①②③ B.①②④ C.①④⑤ D.②③⑤
6.(2021·全国七年级专题练习)如图,下列条件中,不能判断直线a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
7.(2020·山东青岛市·七年级期中)如图,下列不能判定DF∥AC的条件是( )
A.∠A=∠BDF B.∠2=∠4 C.∠1=∠3 D.∠A+∠ADF=180°
8.(2020·陕西宝鸡市·七年级期末)下列条件能判定直线l1∥l2的是( )
A.∠2=∠3 B.∠1=∠3 C.∠4+∠5=180° D.∠2=∠4
9.(2020·广东清远市·八年级期末)如图所示,下列推理及括号中所注明的推理依据错误的是( )
A.∵∠1=∠3,∴AB∥CD(内错角相等,两直线平行)
B.∵AB∥CD,∴∠1=∠3(两直线平行,内错角相等)
C.∵AD∥BC,∴∠BAD+∠ABC=180°(两直线平行,同旁内角互补)
D.∵∠DAM=∠CBM,∴AB∥CD(两直线平行,同位角相等)
10.(2020·山东菏泽市·七年级期末)如图,,C点在EF上,,BC平分,且.下列结论:
①AC平分;②;③;④.其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2020·浙江七年级期末)如图,点B,C,E在同一条直线上,请你写出一个能使成立的条件:_______.(只写一个即可,不添加任何字母或数字)
12.(2019·浙江杭州市·七年级开学考试)如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法,其依据是___.
13.(2020·上海同济大学实验学校)如图,共有_____对同位角,有_____对内错角,有_____对同旁内角.
14.(2020·上海同济大学实验学校)如图,∠1与∠2是直线_____和_____被直线_____所截的一对_____角.
15.(2020·浙江七年级期末)将一块三角板(,)按如图方式放置,使,两点分别放在直线,上,对于给出的四个条件,①,;②;③,④;⑤.能判断直线的有________(填序号).
16.(2020·甘肃白银市·平川区四中七年级期末)如图,下列能判定的条件有_______个.
①;②;③;④.
17.(2019·河南洛阳市·洛阳地矿双语学校七年级月考)如图,现给出下列条件:①,②,③,④,⑤.其中能够得到AB//CD的条件是_______.(只填序号)
18.(2020·江苏扬州市·七年级期中)一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变三角板ACD的位置(其中A点位置始终不变),当∠BAD=_____时,CD∥AB.
19.(2020·安徽蚌埠市·七年级期末)规律探究:同一平面内有直线、、,,,若,,,,,按此规律,与的位置关系是______.
20.(2020·福建泉州市·泉州五中七年级月考)在同一平面内有2019条直线,,如果,,那么①的位置关系是__________②的位置关系是_______________
三、解答题
21.(2020·明光市明湖学校八年级期中)将一副直角三角板按如图所示的方式放置,,,.求证:.
22.(2020·甘肃张掖市·张掖四中八年级期末)已知:如图,,和互余,和互余,求证:.
23.(2021·全国七年级)填写理由:如图,∠1=∠2,∠3=∠4,,试说明.
解:∵∠1=∠2(已知)
∴(______)
即=∠______
∵∠3=∠4,(已知)
∴∠3=∠______(______)
∴∠3=∠______
∴(______)
24.(2020·甘肃兰州市·七年级期末)看图填空,并在括号内注明说理依据.
如图,已知,,,,与平行吗?与平行吗?
解:因为,(已知),
所以.
所以 ( ).
又因为 (已知),
所以.( )
所以.
同理可得, .
所以( ).
所以 (同位角相等,两直线平行).
25.(2019·河南平顶山市·八年级期末)如图,在中,平分交于点,点是边上一点,连接,若,求证:.
26.(2019·全国七年级单元测试)如图,∠BEC=95°,∠ABE=120°,∠DCE=35°,则AB与CD平行吗?请说明理由.
27.(2021·全国七年级专题练习)如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG相交于点H,∠C=∠EFG,∠BFG=∠AEM,求证:AB∥CD.(完成下列填空)
证明:∵∠BFG=∠AEM(已知)
且∠AEM=∠BEC( )
∴∠BEC=∠BFG(等量代换)
∴MC∥ ( )
∴∠C=∠FGD( )
∵∠C=∠EFG(已知)
∴∠ =∠EFG,(等量代换)
∴AB∥CD( )
28.(2020·绍兴市文澜中学七年级期中)如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
29.(2019·广东韶关市·七年级期末)将一副三角板中的两个直角顶点叠放在一起(如图①),其中,,.
(1)猜想与的数量关系,并说明理由;
(2)若,求的度数;
(3)若按住三角板不动,绕顶点转动三角,试探究等于多少度时,并简要说明理由.
30.(2018·贵州遵义市·达兴中学七年级期中)如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
参考答案
1.D 2.C 3.C 4.C 5.D 6.B 7.B 8.B 9.D 10.D
11.∠1=∠2(答案不唯一) 12.同位角相等,两直线平行 13.20 12 12
14.a b c 内错 15.①⑤ 16.1 17.①②⑤ 18.150°或30°.
19.互相垂直. 20.平行 垂直
21.见解析
【详解】
解:由直角三角板的性质可得:
∠C=30°,
∵∠AFD=∠C+∠CDF=75°,
∴∠CDF=45°,
∴∠CDF=∠E,
∴AE∥BC.
22.证明见详解
【详解】
解:证明:∵∠1和∠D互余,∠2和∠D互余,
∴∠1=∠2,
∵∠C=∠1,
∴∠C=∠2,
∴AB∥CD.
23.见解析
【详解】
∵∠1=∠2(已知)
∴(等式的性质)
即=∠ DAC
∵∠3=∠4,(已知)
∴∠3=∠BAE(等量代换)
∴∠3=∠DAC
∴(内错角相等,两直线平行)
24.AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF..
【详解】
解:因为∠1=35°,∠2=35°(已知),
所以∠1=∠2.
所以AC∥BD(同位角相等,两直线平行).
又因为AC⊥AE(已知),
所以∠EAC=90°.(垂直的定义)
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=125°.
所以∠EAB=∠FBG(等量代换).
所以AE∥BF(同位角相等,两直线平行).
故答案为:AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.
25.证明见解析
【详解】
证明:在中,
,
平分
,
26.平行,理由见解析.
【详解】
解:AB∥CD,理由如下:
如图所示,延长BE,交CD于点F,
因为∠BEC=95°,
所以∠CEF=180°-95°=85°.
又因为∠DCE=35°,
所以∠BFC=180°-∠DCE-∠CEF=180°-35°-85°=60°.
因为∠ABE=120°(已知),
所以∠ABE+∠BFC=180°,
所以AB∥CD(同旁内角互补,两直线平行).
27.对顶角相等;GF;同位角相等,两直线平行;FGD;内错角相等,两直线平行
【详解】
证明:∵∠BFG=∠AEM(已知)
且∠AEM=∠BEC(对顶角相等)
∴∠BEC=∠BFG(等量代换)
∴MC∥GF(同位角相等,两直线平行)
∴∠C=∠FGD( 两直线平行,同位角相等)
∵∠C=∠EFG(已知)
∴∠FGD=∠EFG,(等量代换)
∴AB∥CD(内错角相等,两直线平行).
故答案是:对顶角相等;GF;同位角相等,两直线平行;FGD;内错角相等,两直线平行.
28.(1)见解析;(2) 见解析.
【详解】
证明:(1)∵∠1+∠AFE=180°,∠1+∠BCF=180°,
∴∠AFE=∠BCF,
∴BC∥EF;
(2)∵∠BEG=∠EDF,
∴DF∥EH,
∴∠DFE=∠FEH,
又∵BC∥EF,
∴∠FEH=∠2,
又∵∠2=∠3,
∴∠DFE=∠3,
∴DF平分∠AFE.
29.(1),理由详见解析;(2)135°;(3)等于或时,.
【详解】
解:(1),理由如下:
,
;
(2)如图①,设,则,
由(1)可得,
,
,
;
(3)分两种情况:
①如图1所示,当时,,
又,
;
②如图2所示,当时,,
又,
.
综上所述,等于或时,.
30.见解析
详解:(1)∵∠1=∠3,∠2=∠4,∴∠1+∠3+∠2+∠4=2(∠1+∠2),
∵∠1+∠2=90°,∴∠1+∠3+∠2+∠4=180°;
∵∠D+∠B+∠1+∠3+∠2+∠4=360°,∴∠D+∠B=180°,
∴DE∥BC.
(2)成立.
如图2,连接EC;
∵∠1=∠3,∠2=∠4,且∠1+∠2=90°,∴∠3+∠4=∠1+∠2=90°;
∵∠EAC=90°,∴∠AEC+∠ACE=180°-90°=90°,
∴∠AEC+∠ACE+∠3+∠4=180°,
∴DE∥BC,
即(1)中的结论仍成立.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
