2020-2021学年高二数学选修1-1第二章2.1.1 椭圆及其标准方程 课件(共26张PPT)
文档属性
| 名称 | 2020-2021学年高二数学选修1-1第二章2.1.1 椭圆及其标准方程 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 874.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
人教版
A版
高二数学选修1-1
§2.1.1椭圆及其标准方程
1:准备一张圆形纸片。设圆心是O,在圆内不是圆心处取一点,标上F。
2.把纸片翘起一角,使圆周正好通过F。
把纸片抹平,于是就留下一条折痕。为了清楚些,你可以再折痕上标上红线。如图。
如何用折纸法将圆形变成了椭圆形?
一.课题引入:趣味数学
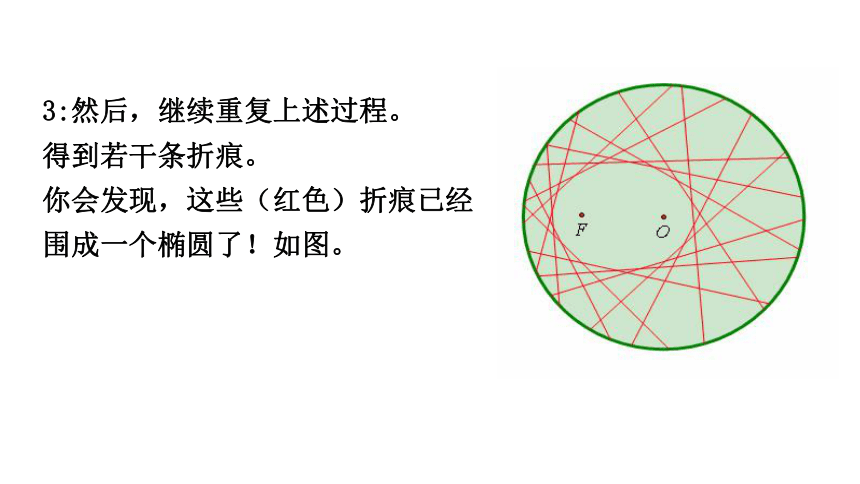
3:然后,继续重复上述过程。
得到若干条折痕。
你会发现,这些(红色)折痕已经围成一个椭圆了!如图。
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
北京天坛公园回音壁
探究1:取一条定长的细绳,把它的两端固定在图板的同一个点处,套上铅笔,拉紧绳子,慢慢移动笔尖,这时笔尖画出的轨迹是什么呢?
圆
探究与思考:
探究2:取一条定长的细绳,把它的两端拉开一段距离,分别固定在图板的两个点处,套上铅笔,拉紧绳子,慢慢移动笔尖,这时笔尖画出的轨迹是什么呢?
探究与思考:
椭圆
数
学
实
验
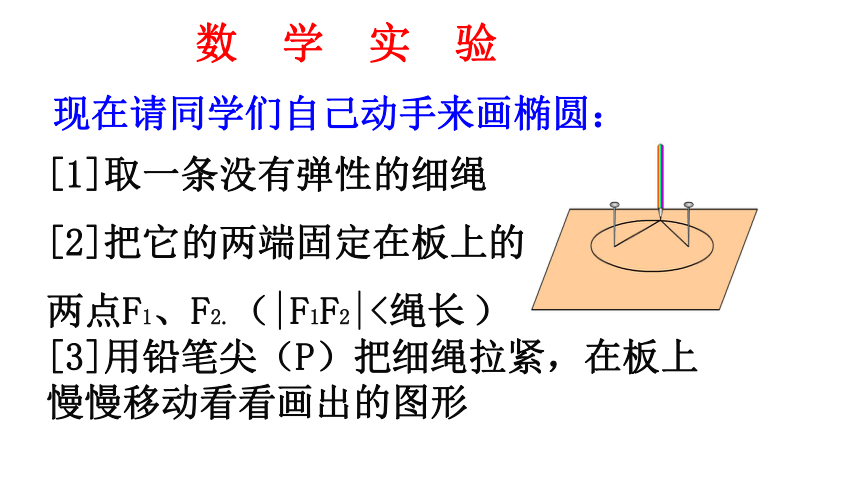
[1]取一条没有弹性的细绳
[2]把它的两端固定在板上的
两点F1、F2.(|F1F2|<绳长
)
[3]用铅笔尖(P)把细绳拉紧,在板上慢慢移动看看画出的图形
现在请同学们自己动手来画椭圆:
思考3:细绳的长度变了没有呢?
是
思考1:椭圆是平面图形吗?
椭圆上的点P到两个定点F1,F2的距离之和就是绳长即定值
思考4:拉紧细绳起到什么作用呢?
不变
思考2:在画椭圆的过程中,细绳的两端的位置是固定的还是运动的?
固定
思考7:这现象你能用文字语言来概括出椭圆的定义来呢?
思考6:移动笔尖时动点P满足什么几何条件?
|PF1|+|PF2|=定值(即绳长)
思考5:绳长与这两个定点的大小关系又怎么样?
绳长大于两个定点的距离
温馨提醒:椭圆定义的要点
(1)必须在平面内;
(2)两个定点---两点间的距离确定即焦距;(常记作2c)
(3)常数---轨迹上任意点到两定点距离之和确定.
(常记作:2a,且
2a>2c)
椭圆定义
文字语言:平面内与两个定点(
)的距离之和等于
常
数(
)的点的轨迹叫椭圆。
符号语言:|PF1|+|PF2|=常数
焦点
大于|F1F2|
思考10:若2a轨迹是一条线段
轨迹不存在
探究3:取一条定长的细绳,把它的两端拉开一段距离等于细绳的长度,分别固定在图板的两个点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖画出的轨迹是什么呢?
思考8:2a=2c
或
2a<2c?
思考9:若2a=F1F2轨迹是什么呢?
例题1:平面上有动点P到两个定点F1
(-3,0)、F2
(3,0)
的距离之和为8,则动点P的轨迹是(
)
A.圆
B.
椭圆
C.
线段
D.直线
例题巩固:
B
C
变式:平面上有动点P到两个定点F1
(-3,0)、F2
(3,0)
的距离之和为6,则动点P的轨迹是(
)
A.圆
B.
椭圆
C.
线段
D.直线
?
求动点轨迹方程的一般步骤:
(1)建立适当的坐标系,用有序实数对(x,y)
表示曲线上任意一点M的坐标;即建系,设点
(2)写出适合条件
P(M)
;即列限制条件
(3)用坐标表示条件P(M),列出方程
;即代方程
(4)化方程为最简形式;即化简
(5)证明以化简后的方程为所求方程(可以省略
不写,如有特殊情况,可以适当予以说明)
坐标法
二、椭圆方程推导的准备
?
探讨建立平面直角坐标系的方案
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
求椭圆的方程的推导:
原
则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)
(“对称”、“简洁”)
O
x
y
O
x
y
O
x
y
解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x,
y)是椭圆上任意一点,椭圆的焦距2c(c>0),M与F1和F2的距离的和等于常数2a(2a>2c)
,则F1、F2的坐标分别是方案一:(?c,0)、(c,0)
;
{方案二:
(0,-c)、(0,c)}
以下以方案一为说明,方案二进行类比。
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
代入坐标:
x
F1
F2
M
0
y
b的引入:
a
c
b
y
1
o
F
x
2
F
M
a
c
b
焦点在y轴:
焦点在x轴:
椭圆的标准方程:
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
它所表示的椭圆的焦点在x轴上,焦点是
中心在坐标原点的椭圆
方程
,其中
它所表示的椭圆的焦点在y轴上,焦点是
中心在坐标原点的椭圆
方程
,其中
答:在
X
轴。(-4,0)和(4,0)
答:在
y
轴。(0,-5)和(0,5)
答:在
y
轴。(0,-1)和(0,1)
判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。
例2判定下列是不是椭圆方程?若是椭圆,求它的焦点在什么轴上,并指明a2、b2,写出焦点坐标。
解:连接AO,与折痕有一个交点P,连接OP,PF,PA
用折纸法将圆形变成了椭圆形,如何求解它的方程?
课题引入:
∵|PF|=|PA|,
∴|OP|+|PF|=|OA|=R
点P的轨迹就是椭圆。
设R=10,|OF|=6.即|OP|+|PF|=10
P
例题3.求适合下列条件的椭圆的标准方程:
(2)焦点为F1(0,-3)
,且a=5;
(1)a=
,b=1,焦点在x轴上;
(3)两个焦点分别是F2(2,0),且过P(2,3)点;
(4)经过点P(-2,0)和Q(0,-3).
图
形
方
程
焦
点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a
(2a>2c>0)
定
义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
总结与反思:
椭圆方程有特点
系数为正加相连
分母较大焦点定
右边数“1”记心间
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标
原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆
项分母较大.
焦点在y轴的椭圆
项分母较大.
练习1.
已知椭圆的方程为:
,请填空:
(1)
a=__,b=__,c=__,焦点坐标为
,焦距等于__.
(2)已知椭圆上一点P到一个焦点的距离为3,则P到另一个焦点的距离__
变式:
若椭圆的方程为
,试口答完成.
5
4
3
6
(-3,0)、(3,0)
7
练习2:若方程?
,表示焦点在?y
轴上的椭圆,则k的取值范围是_______。
变式2:方程
,分别求方程满足
下列条件的m的取值范围:
①表示一个圆;
②表示一个椭圆;
③表示焦点在x轴上的椭圆。
m=8
回顾小结:
求椭圆标准方程的方法
一种方法:
二类方程:
三个意识:
求美意识,
求简意识,前瞻意识
作业布置:
选修1-1
书本P42
A组1、2
人教版
A版
高二数学选修1-1
§2.1.1椭圆及其标准方程
1:准备一张圆形纸片。设圆心是O,在圆内不是圆心处取一点,标上F。
2.把纸片翘起一角,使圆周正好通过F。
把纸片抹平,于是就留下一条折痕。为了清楚些,你可以再折痕上标上红线。如图。
如何用折纸法将圆形变成了椭圆形?
一.课题引入:趣味数学
3:然后,继续重复上述过程。
得到若干条折痕。
你会发现,这些(红色)折痕已经围成一个椭圆了!如图。
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
北京天坛公园回音壁
探究1:取一条定长的细绳,把它的两端固定在图板的同一个点处,套上铅笔,拉紧绳子,慢慢移动笔尖,这时笔尖画出的轨迹是什么呢?
圆
探究与思考:
探究2:取一条定长的细绳,把它的两端拉开一段距离,分别固定在图板的两个点处,套上铅笔,拉紧绳子,慢慢移动笔尖,这时笔尖画出的轨迹是什么呢?
探究与思考:
椭圆
数
学
实
验
[1]取一条没有弹性的细绳
[2]把它的两端固定在板上的
两点F1、F2.(|F1F2|<绳长
)
[3]用铅笔尖(P)把细绳拉紧,在板上慢慢移动看看画出的图形
现在请同学们自己动手来画椭圆:
思考3:细绳的长度变了没有呢?
是
思考1:椭圆是平面图形吗?
椭圆上的点P到两个定点F1,F2的距离之和就是绳长即定值
思考4:拉紧细绳起到什么作用呢?
不变
思考2:在画椭圆的过程中,细绳的两端的位置是固定的还是运动的?
固定
思考7:这现象你能用文字语言来概括出椭圆的定义来呢?
思考6:移动笔尖时动点P满足什么几何条件?
|PF1|+|PF2|=定值(即绳长)
思考5:绳长与这两个定点的大小关系又怎么样?
绳长大于两个定点的距离
温馨提醒:椭圆定义的要点
(1)必须在平面内;
(2)两个定点---两点间的距离确定即焦距;(常记作2c)
(3)常数---轨迹上任意点到两定点距离之和确定.
(常记作:2a,且
2a>2c)
椭圆定义
文字语言:平面内与两个定点(
)的距离之和等于
常
数(
)的点的轨迹叫椭圆。
符号语言:|PF1|+|PF2|=常数
焦点
大于|F1F2|
思考10:若2a
轨迹不存在
探究3:取一条定长的细绳,把它的两端拉开一段距离等于细绳的长度,分别固定在图板的两个点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖画出的轨迹是什么呢?
思考8:2a=2c
或
2a<2c?
思考9:若2a=F1F2轨迹是什么呢?
例题1:平面上有动点P到两个定点F1
(-3,0)、F2
(3,0)
的距离之和为8,则动点P的轨迹是(
)
A.圆
B.
椭圆
C.
线段
D.直线
例题巩固:
B
C
变式:平面上有动点P到两个定点F1
(-3,0)、F2
(3,0)
的距离之和为6,则动点P的轨迹是(
)
A.圆
B.
椭圆
C.
线段
D.直线
?
求动点轨迹方程的一般步骤:
(1)建立适当的坐标系,用有序实数对(x,y)
表示曲线上任意一点M的坐标;即建系,设点
(2)写出适合条件
P(M)
;即列限制条件
(3)用坐标表示条件P(M),列出方程
;即代方程
(4)化方程为最简形式;即化简
(5)证明以化简后的方程为所求方程(可以省略
不写,如有特殊情况,可以适当予以说明)
坐标法
二、椭圆方程推导的准备
?
探讨建立平面直角坐标系的方案
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
求椭圆的方程的推导:
原
则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)
(“对称”、“简洁”)
O
x
y
O
x
y
O
x
y
解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x,
y)是椭圆上任意一点,椭圆的焦距2c(c>0),M与F1和F2的距离的和等于常数2a(2a>2c)
,则F1、F2的坐标分别是方案一:(?c,0)、(c,0)
;
{方案二:
(0,-c)、(0,c)}
以下以方案一为说明,方案二进行类比。
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
代入坐标:
x
F1
F2
M
0
y
b的引入:
a
c
b
y
1
o
F
x
2
F
M
a
c
b
焦点在y轴:
焦点在x轴:
椭圆的标准方程:
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
它所表示的椭圆的焦点在x轴上,焦点是
中心在坐标原点的椭圆
方程
,其中
它所表示的椭圆的焦点在y轴上,焦点是
中心在坐标原点的椭圆
方程
,其中
答:在
X
轴。(-4,0)和(4,0)
答:在
y
轴。(0,-5)和(0,5)
答:在
y
轴。(0,-1)和(0,1)
判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。
例2判定下列是不是椭圆方程?若是椭圆,求它的焦点在什么轴上,并指明a2、b2,写出焦点坐标。
解:连接AO,与折痕有一个交点P,连接OP,PF,PA
用折纸法将圆形变成了椭圆形,如何求解它的方程?
课题引入:
∵|PF|=|PA|,
∴|OP|+|PF|=|OA|=R
点P的轨迹就是椭圆。
设R=10,|OF|=6.即|OP|+|PF|=10
P
例题3.求适合下列条件的椭圆的标准方程:
(2)焦点为F1(0,-3)
,且a=5;
(1)a=
,b=1,焦点在x轴上;
(3)两个焦点分别是F2(2,0),且过P(2,3)点;
(4)经过点P(-2,0)和Q(0,-3).
图
形
方
程
焦
点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a
(2a>2c>0)
定
义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
总结与反思:
椭圆方程有特点
系数为正加相连
分母较大焦点定
右边数“1”记心间
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标
原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆
项分母较大.
焦点在y轴的椭圆
项分母较大.
练习1.
已知椭圆的方程为:
,请填空:
(1)
a=__,b=__,c=__,焦点坐标为
,焦距等于__.
(2)已知椭圆上一点P到一个焦点的距离为3,则P到另一个焦点的距离__
变式:
若椭圆的方程为
,试口答完成.
5
4
3
6
(-3,0)、(3,0)
7
练习2:若方程?
,表示焦点在?y
轴上的椭圆,则k的取值范围是_______。
变式2:方程
,分别求方程满足
下列条件的m的取值范围:
①表示一个圆;
②表示一个椭圆;
③表示焦点在x轴上的椭圆。
m=8
回顾小结:
求椭圆标准方程的方法
一种方法:
二类方程:
三个意识:
求美意识,
求简意识,前瞻意识
作业布置:
选修1-1
书本P42
A组1、2
