2020-2021学年北师大版七年级下册数学 2.2探索直线平行的条件 同步练习(word版,含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级下册数学 2.2探索直线平行的条件 同步练习(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 111.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 22:46:33 | ||
图片预览


文档简介
2.2探索直线平行的条件 同步练习
一.选择题
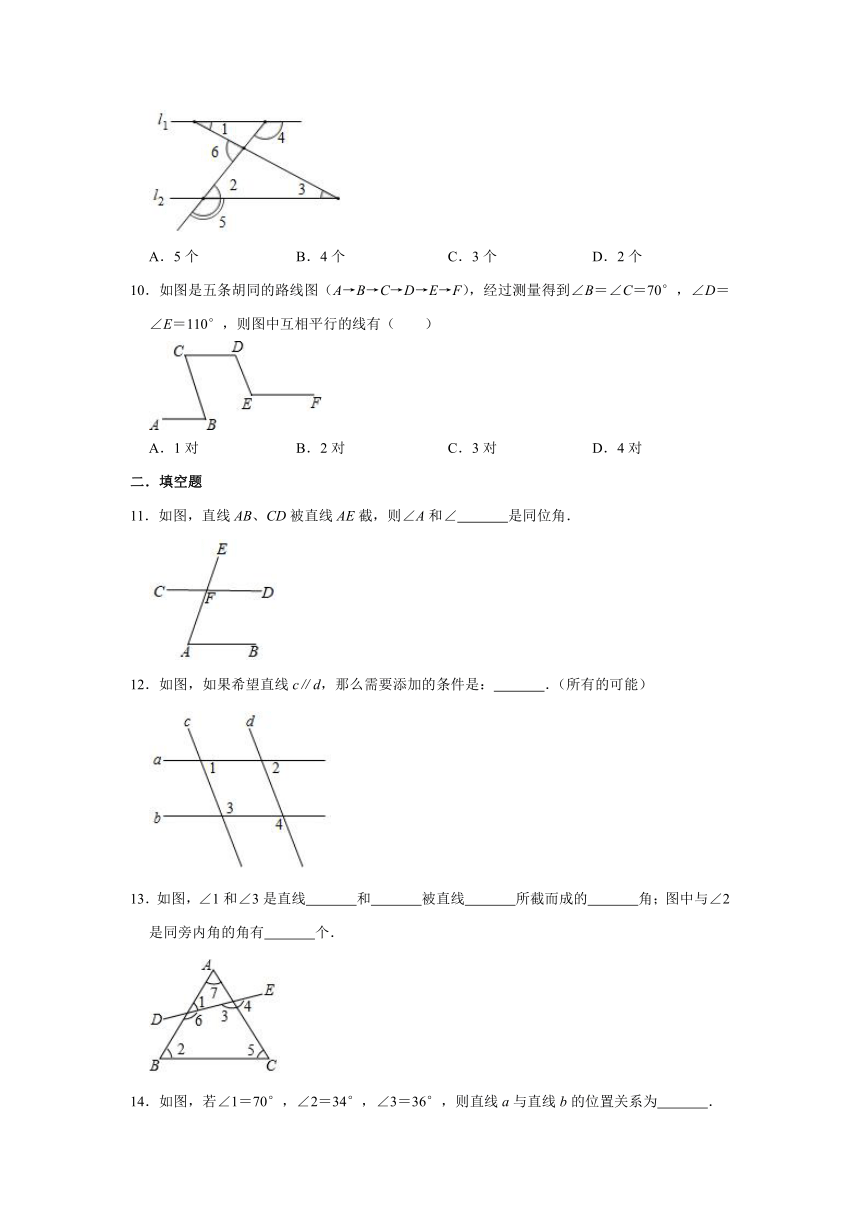
1.如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
A.∠1=∠6 B.∠4=∠6 C.∠1=∠3 D.∠2=∠5
3.如图,要得到a∥b,则需要条件( )
A.∠1+∠2=180° B.∠1=∠2 C.∠1+∠2=90° D.∠1+∠2=120°
4.下列图形中,能根据∠1=∠2判断AB∥CD的是( )
A. B.
C. D.
5.如图,与∠B互为同旁内角的角有( )个
A.2 B.3 C.4 D.5
6.如图,下列判断正确的是( )
A.∠1,∠2,∠6互为邻补角 B.∠2与∠4是同位角
C.∠3与∠6是同旁内角 D.∠5与∠3是内错角
7.如图,下列条件中,能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠2
C.∠3=∠4 D.∠C+∠ADC=180°
8.如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
A.AB∥CD∥EF B.CD∥EF
C.AB∥EF D.AB∥CD∥EF,BC∥DE
9.如图,下列条件:①∠1=∠2;②∠4=∠5:③∠2+∠5=180°;④∠1=∠3;其中能判断直线l1∥l2的有( )
A.5个 B.4个 C.3个 D.2个
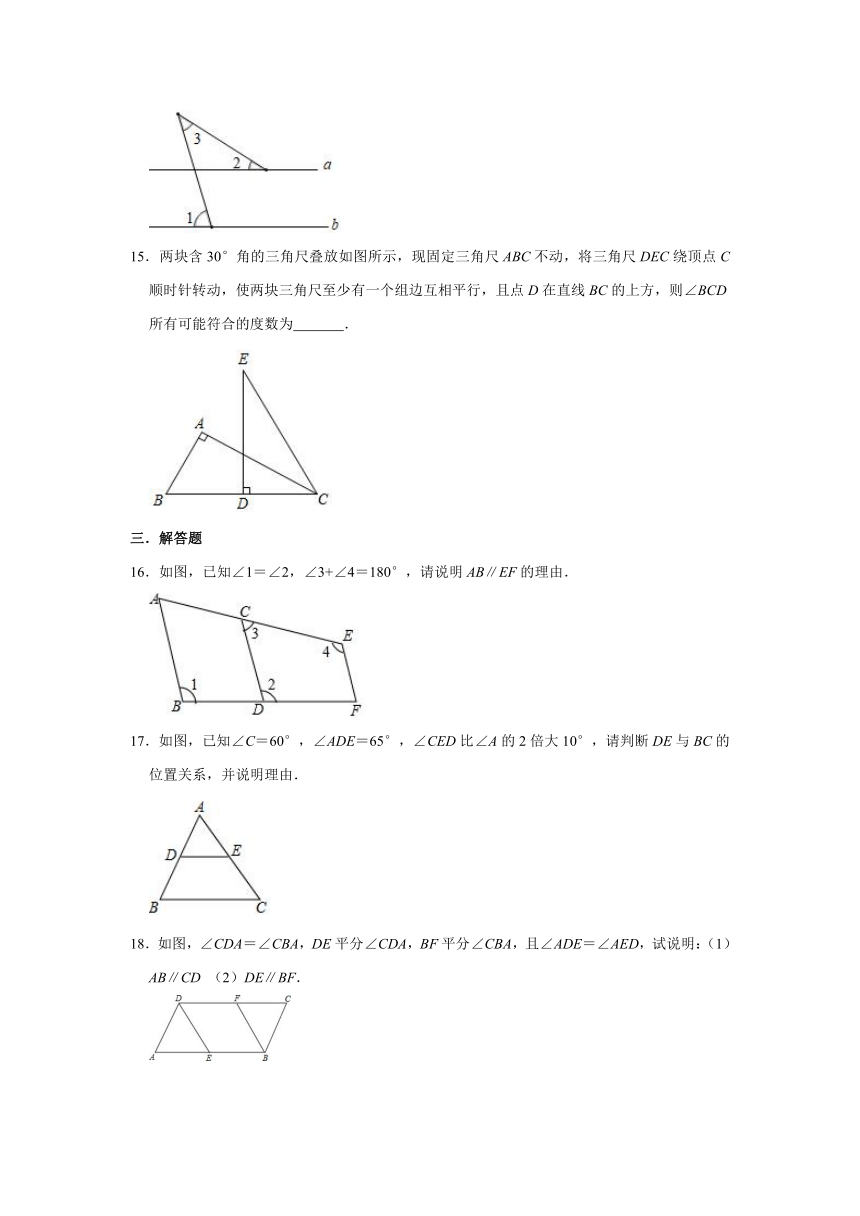
10.如图是五条胡同的路线图(A→B→C→D→E→F),经过测量得到∠B=∠C=70°,∠D=∠E=110°,则图中互相平行的线有( )
A.1对 B.2对 C.3对 D.4对
二.填空题
11.如图,直线AB、CD被直线AE截,则∠A和∠ 是同位角.
12.如图,如果希望直线c∥d,那么需要添加的条件是: .(所有的可能)
13.如图,∠1和∠3是直线 和 被直线 所截而成的 角;图中与∠2是同旁内角的角有 个.
14.如图,若∠1=70°,∠2=34°,∠3=36°,则直线a与直线b的位置关系为 .
15.两块含30°角的三角尺叠放如图所示,现固定三角尺ABC不动,将三角尺DEC绕顶点C顺时针转动,使两块三角尺至少有一个组边互相平行,且点D在直线BC的上方,则∠BCD所有可能符合的度数为 .
三.解答题
16.如图,已知∠1=∠2,∠3+∠4=180°,请说明AB∥EF的理由.
17.如图,已知∠C=60°,∠ADE=65°,∠CED比∠A的2倍大10°,请判断DE与BC的位置关系,并说明理由.
18.如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠ADE=∠AED,试说明:(1)AB∥CD (2)DE∥BF.
参考答案
一.选择题
1.解:根据内错角的定义可知:∠1和∠4是内错角,
故选:C.
2.解:A、∠1=∠6,不能判定a∥b,不符合题意;
B、∵∠4=∠6,∠2=∠4,∴∠2=∠6,∴a∥b,符合题意;
C、∠1=∠3,不能判定a∥b,不符合题意;
D、∵∠2=∠5,不能判定a∥b,不符合题意;
故选:B.
3.解:∵∠1=∠2,
∴a∥b.
故选:B.
4.解:A、∵∠1=∠2,∴AC∥BD,错误;
B、∠1=∠2,不能判断直线平行,错误;
C、∵∠1=∠2,∴AB∥CD,正确;
D、∠1=∠2,不能判断直线平行,错误;
故选:C.
5.解:与∠B互为同旁内角的角有∠AOB,∠BAO,∠BCD,∠BAD共4个.
故选:C.
6.解:A、只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角,故∠1,∠2,∠6互为邻补角,错误;
B、∠2与∠4不是同位角,错误;
C、∠3与∠6是同旁内角,正确;
D、∠5与∠3不是内错角,错误;
故选:C.
7.解:∵∠3=∠4,
∴AB∥CD,
故选:C.
8.解:∵∠1=∠2=∠3=∠4,
∴AB∥CD,BC∥DE,CD∥EF,
∴AB∥CD∥EF.
故选:D.
9.解:①∵∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③∵∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
④∵∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:D.
10.解:∵∠B=∠C=70°,
∴AB∥CD.
∵∠D=∠E=110°,
∴CD∥EF,
∴AB∥EF.
∵∠C+∠D=70°+110°=180°,
∴BC∥DE.
故选:D.
二.填空题
11.解:直线AB、CD被直线AE截,则∠A和∠EFD是同位角,
故答案为:EFD.
12.解:当∠1=∠2时,根据同位角相等,两直线平行可得c∥d;
当∠3=∠4时,根据内错角相等,两直线平行可得c∥d;
故答案为:∠1=∠2或∠3=∠4.
13.解:∠1和∠3是直线AB和AC被直线DE所截而成的内错角;图中与∠2 是同旁内角的角有∠6、∠5、∠7,共3个,
故答案为:AB、AC、DE、内错,3.
14.解:∵∠4=∠2+∠3,∠2=34°,∠3=36°,
∴∠4=34+36°=70°,
∵∠1=70°,
∴∠4=∠1,
∴a∥b.
故答案为a∥b.
15.解:如图1中,当DE∥AB时,∠BCD=30°
如图2中,当AB∥CE时,∠BCD=60°.
如图3中,当DE∥BC时,∠BCD=90°.
如图4中,当AB∥CD时,∠BCD=120°
综上所述,满足条件的∠BCD的值为30°或60°和90°或120°.
三.解答题
16.解:∵∠1=∠2,
∴AB∥CD,
∵∠3+∠4=180°,
∴CD∥EF,
∴AB∥EF.
17.解:DE∥BC,理由如下:
设∠A为x°,所以∠CED为2x°+10°,
∵∠CED=∠A+∠ADE,
可得:2x°+10°=x°+65°,
解得:x=55,
∴∠DEC=2×55°+10°=120°,
∵∠C=60°,
∴∠C+∠CED=180°,
∴DE∥BC,
18.证明:(1)∵DE平分∠CDA,
∴∠ADE=∠EDC,
而∠ADE=∠AED,
∴∠EDC=∠AED,
∴AB∥CD;
(2)∵BF平分∠CBA,
∴∠ABF=∠ABC,
∵∠AED=∠ADE=∠ADC,
而∠CDA=∠CBA,
∴∠AED=∠ABF,
∴DE∥BF.
一.选择题
1.如图,∠1的内错角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,直线a、b被直线c所截,下列条件能使a∥b的是( )
A.∠1=∠6 B.∠4=∠6 C.∠1=∠3 D.∠2=∠5
3.如图,要得到a∥b,则需要条件( )
A.∠1+∠2=180° B.∠1=∠2 C.∠1+∠2=90° D.∠1+∠2=120°
4.下列图形中,能根据∠1=∠2判断AB∥CD的是( )
A. B.
C. D.
5.如图,与∠B互为同旁内角的角有( )个
A.2 B.3 C.4 D.5
6.如图,下列判断正确的是( )
A.∠1,∠2,∠6互为邻补角 B.∠2与∠4是同位角
C.∠3与∠6是同旁内角 D.∠5与∠3是内错角
7.如图,下列条件中,能判断AB∥CD的是( )
A.∠1=∠2 B.∠3=∠2
C.∠3=∠4 D.∠C+∠ADC=180°
8.如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
A.AB∥CD∥EF B.CD∥EF
C.AB∥EF D.AB∥CD∥EF,BC∥DE
9.如图,下列条件:①∠1=∠2;②∠4=∠5:③∠2+∠5=180°;④∠1=∠3;其中能判断直线l1∥l2的有( )
A.5个 B.4个 C.3个 D.2个
10.如图是五条胡同的路线图(A→B→C→D→E→F),经过测量得到∠B=∠C=70°,∠D=∠E=110°,则图中互相平行的线有( )
A.1对 B.2对 C.3对 D.4对
二.填空题
11.如图,直线AB、CD被直线AE截,则∠A和∠ 是同位角.
12.如图,如果希望直线c∥d,那么需要添加的条件是: .(所有的可能)
13.如图,∠1和∠3是直线 和 被直线 所截而成的 角;图中与∠2是同旁内角的角有 个.
14.如图,若∠1=70°,∠2=34°,∠3=36°,则直线a与直线b的位置关系为 .
15.两块含30°角的三角尺叠放如图所示,现固定三角尺ABC不动,将三角尺DEC绕顶点C顺时针转动,使两块三角尺至少有一个组边互相平行,且点D在直线BC的上方,则∠BCD所有可能符合的度数为 .
三.解答题
16.如图,已知∠1=∠2,∠3+∠4=180°,请说明AB∥EF的理由.
17.如图,已知∠C=60°,∠ADE=65°,∠CED比∠A的2倍大10°,请判断DE与BC的位置关系,并说明理由.
18.如图,∠CDA=∠CBA,DE平分∠CDA,BF平分∠CBA,且∠ADE=∠AED,试说明:(1)AB∥CD (2)DE∥BF.
参考答案
一.选择题
1.解:根据内错角的定义可知:∠1和∠4是内错角,
故选:C.
2.解:A、∠1=∠6,不能判定a∥b,不符合题意;
B、∵∠4=∠6,∠2=∠4,∴∠2=∠6,∴a∥b,符合题意;
C、∠1=∠3,不能判定a∥b,不符合题意;
D、∵∠2=∠5,不能判定a∥b,不符合题意;
故选:B.
3.解:∵∠1=∠2,
∴a∥b.
故选:B.
4.解:A、∵∠1=∠2,∴AC∥BD,错误;
B、∠1=∠2,不能判断直线平行,错误;
C、∵∠1=∠2,∴AB∥CD,正确;
D、∠1=∠2,不能判断直线平行,错误;
故选:C.
5.解:与∠B互为同旁内角的角有∠AOB,∠BAO,∠BCD,∠BAD共4个.
故选:C.
6.解:A、只有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角,故∠1,∠2,∠6互为邻补角,错误;
B、∠2与∠4不是同位角,错误;
C、∠3与∠6是同旁内角,正确;
D、∠5与∠3不是内错角,错误;
故选:C.
7.解:∵∠3=∠4,
∴AB∥CD,
故选:C.
8.解:∵∠1=∠2=∠3=∠4,
∴AB∥CD,BC∥DE,CD∥EF,
∴AB∥CD∥EF.
故选:D.
9.解:①∵∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③∵∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
④∵∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:D.
10.解:∵∠B=∠C=70°,
∴AB∥CD.
∵∠D=∠E=110°,
∴CD∥EF,
∴AB∥EF.
∵∠C+∠D=70°+110°=180°,
∴BC∥DE.
故选:D.
二.填空题
11.解:直线AB、CD被直线AE截,则∠A和∠EFD是同位角,
故答案为:EFD.
12.解:当∠1=∠2时,根据同位角相等,两直线平行可得c∥d;
当∠3=∠4时,根据内错角相等,两直线平行可得c∥d;
故答案为:∠1=∠2或∠3=∠4.
13.解:∠1和∠3是直线AB和AC被直线DE所截而成的内错角;图中与∠2 是同旁内角的角有∠6、∠5、∠7,共3个,
故答案为:AB、AC、DE、内错,3.
14.解:∵∠4=∠2+∠3,∠2=34°,∠3=36°,
∴∠4=34+36°=70°,
∵∠1=70°,
∴∠4=∠1,
∴a∥b.
故答案为a∥b.
15.解:如图1中,当DE∥AB时,∠BCD=30°
如图2中,当AB∥CE时,∠BCD=60°.
如图3中,当DE∥BC时,∠BCD=90°.
如图4中,当AB∥CD时,∠BCD=120°
综上所述,满足条件的∠BCD的值为30°或60°和90°或120°.
三.解答题
16.解:∵∠1=∠2,
∴AB∥CD,
∵∠3+∠4=180°,
∴CD∥EF,
∴AB∥EF.
17.解:DE∥BC,理由如下:
设∠A为x°,所以∠CED为2x°+10°,
∵∠CED=∠A+∠ADE,
可得:2x°+10°=x°+65°,
解得:x=55,
∴∠DEC=2×55°+10°=120°,
∵∠C=60°,
∴∠C+∠CED=180°,
∴DE∥BC,
18.证明:(1)∵DE平分∠CDA,
∴∠ADE=∠EDC,
而∠ADE=∠AED,
∴∠EDC=∠AED,
∴AB∥CD;
(2)∵BF平分∠CBA,
∴∠ABF=∠ABC,
∵∠AED=∠ADE=∠ADC,
而∠CDA=∠CBA,
∴∠AED=∠ABF,
∴DE∥BF.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
