2020-2021学年人教版数学七年级下册6.1平方根课件(21张)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册6.1平方根课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 737.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 23:35:52 | ||
图片预览





文档简介
6.1.3平方根
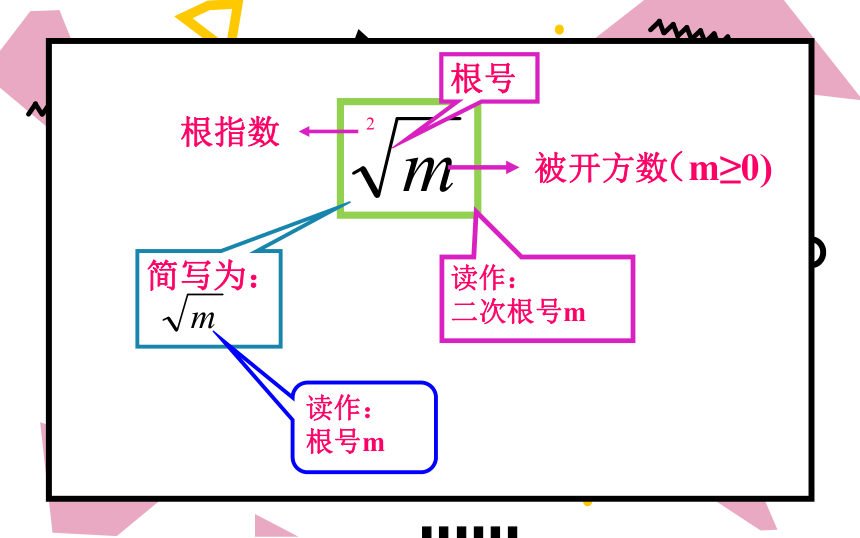
2
根指数
被开方数
读作:
二次根号m
简写为:
读作:
根号m
(m≥0)
根号
1、我们已经学习过哪些运算?它们中互为逆运算的是?
解:加法、减法、乘法、除法、乘方
加法与减法互逆;乘法与除法互逆。
2、乘方有没有逆运算?
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
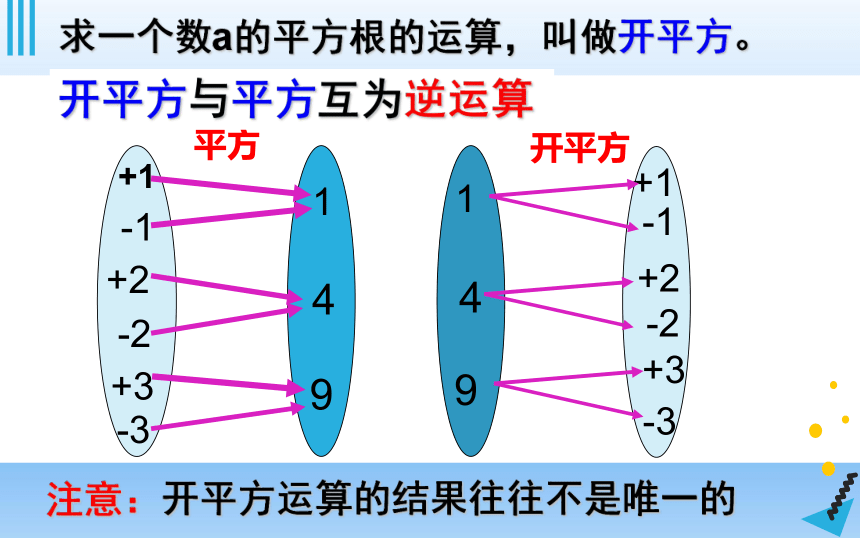
开平方
平方
开平方与平方互为逆运算
求一个数a的平方根的运算,叫做开平方。
注意:开平方运算的结果往往不是唯一的
1
4
9
填空:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
16
25
49
81
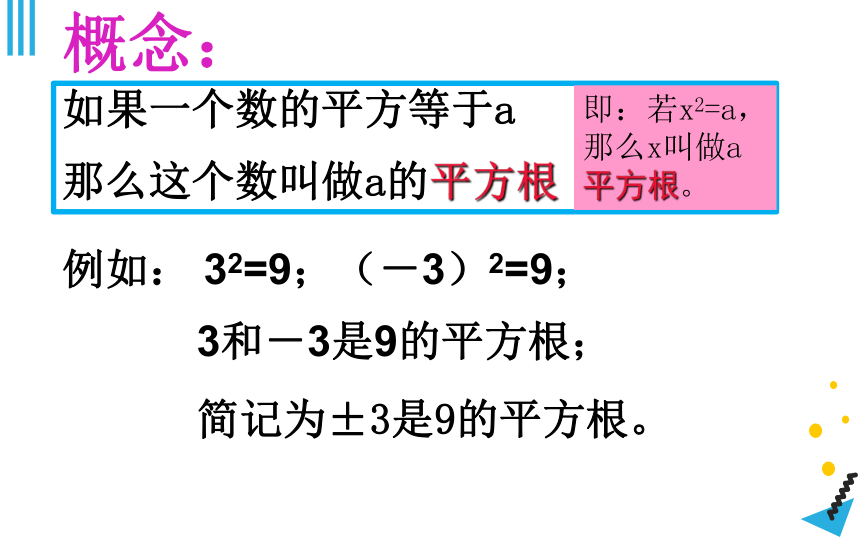
如果一个数的平方等于a
那么这个数叫做a的平方根
如果一个数的平方等于a
那么这个数叫做a的平方根
即:若x2=a,那么x叫做a平方根。
例如: 32=9;(-3)2=9;
3和-3是9的平方根;
简记为±3是9的平方根。
概念:
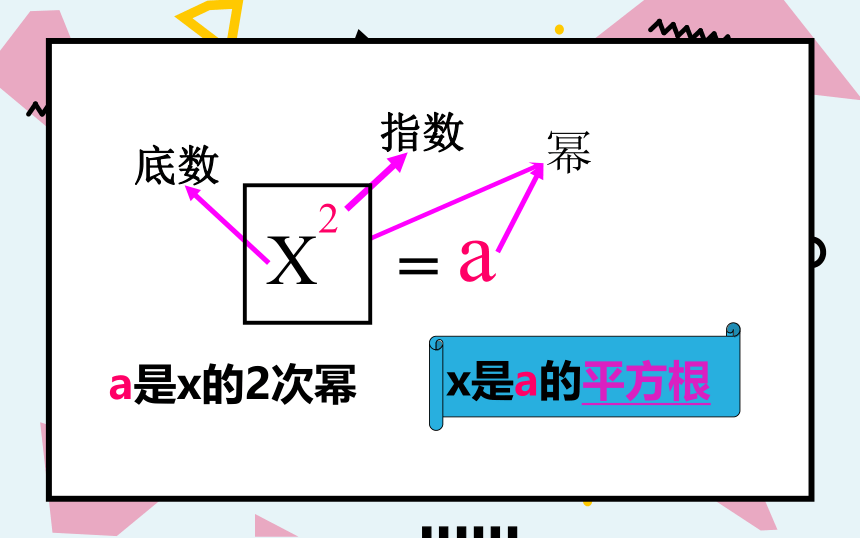
a是x的2次幂
x是a的平方根
X2
底数
指数
幂
=
a
判断下列各数有没有平方根,若有,求其平方根。若没有,说明为什么。
(1) 0.81 (2) (3) (4)(-2 )2
(5 )9 (6)0 (7)-100 (8) 10
2
学以致用
一个正数有两个平方根,它们互为相反数
零有一个平方根,它是零本身
负数没有平方根
1、检验下面各题中前面的数是不是后面的数的平方根。
(1)±12 , 144
(2)±0.2 , 0.04
(3)102 ,104
(4)14 ,256
是
是
是
不是
随堂练习
2、选择题
(1) 0.01的平方根是 ( )
(A)0.1 (B)±0.1 (C)0.0001 (D)±0.0001
(2)∵ (0.3)2 = 0.09
∴ ( )
(A)0.09 是 0.3的平方根. (B)0.09是0.3的3倍.
(C)0.3 是0.09 的平方根. (D)0.3不是0.09的平方根.
B
C
随堂练习
1. 判断下列说法是否正确:
(1)-9的平方根是-3 ( )
(2)49的平方根是7 ( )
(3)(-2)2的平方根是±2 ( )
(4)1 的平方根是 1 ( )
(5)-1 是 1的平方根 ( )
(6)7的平方根是±49 ( )
(7)若X2 = 16, 则X = 4 ( )
×
×
√
×
√
×
×
3 有没有平方根 ?
若有 ,怎样表示?
没有,说明为什么 ?
负的平方根表示为:
即m的平方根表示为:
+
-
±
一个数的平方根的表示方法:
±
± =±7
3的平方根是:
±
如:49 的平方根是
则:
非负数m
正的平方根表示为:
(m≥0)
(1)100 (2) (3)0.0001
解:
例1.求下列各数的平方根:
(1)∵( )2 =100,
∴ 100的平方根为±10.
∴ 的平方根为
(2)∵( )2 =
解(3)∵( )2 =0.0001,
∴ 0.0001的平方根为±0.01.
练习:求下列各数的平方根:
(1) 1.69
(1)100 (2) (3)0.0001
例1.求下列各数的平方根:
1.本节课引入了新的运算——开方运算,开方和乘方互为逆运算,从而完备了初等代数中六种基本代数运算(加、减、乘、除、乘方、开方),这对代数内容学习有着重要的意义。
2.本节主要学习了:
①平方根的概念
②平方根的性质:一个正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根
③平方根的表示方法
④求一个数的平方根的运算—开平方,应分清平方运算与开平方运算的区别与联系
小结 & 归纳
下列各数有平方根吗?说明理由。
(1)- 4 ( )
(2)(- 4)2 ( )
(3)- 42 ( )
(4)0 ( )
(5)(-2)3 ( )
(6)|3| ( )
(7) ( )
(8)x2+1 ( )
当这个数为正数时,它有两个平方根;当这个数为0时,它有一个平方根0;当这个数为负数时,它没有平方根。
√
×
×
√
×
√
判断一个数有没有平方根,只要看这个数的符号。
×
√
练习
a
121
196
0.81
104
a的平方根
±11
±14
±0.9
±100
2.填表:
解:∵正数有两个平方根,它们互为相反数。
(1)x的一个平方根是3,则另一个平方根是 ,x= 。
-3
9
(2)3y-22和2y-3是m的两个平方根,试求m的值。
∴ 3y-22+2y-3=0
∴ y=5
∴m=
练习 3
就此别过。
2
根指数
被开方数
读作:
二次根号m
简写为:
读作:
根号m
(m≥0)
根号
1、我们已经学习过哪些运算?它们中互为逆运算的是?
解:加法、减法、乘法、除法、乘方
加法与减法互逆;乘法与除法互逆。
2、乘方有没有逆运算?
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
开平方与平方互为逆运算
求一个数a的平方根的运算,叫做开平方。
注意:开平方运算的结果往往不是唯一的
1
4
9
填空:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
16
25
49
81
如果一个数的平方等于a
那么这个数叫做a的平方根
如果一个数的平方等于a
那么这个数叫做a的平方根
即:若x2=a,那么x叫做a平方根。
例如: 32=9;(-3)2=9;
3和-3是9的平方根;
简记为±3是9的平方根。
概念:
a是x的2次幂
x是a的平方根
X2
底数
指数
幂
=
a
判断下列各数有没有平方根,若有,求其平方根。若没有,说明为什么。
(1) 0.81 (2) (3) (4)(-2 )2
(5 )9 (6)0 (7)-100 (8) 10
2
学以致用
一个正数有两个平方根,它们互为相反数
零有一个平方根,它是零本身
负数没有平方根
1、检验下面各题中前面的数是不是后面的数的平方根。
(1)±12 , 144
(2)±0.2 , 0.04
(3)102 ,104
(4)14 ,256
是
是
是
不是
随堂练习
2、选择题
(1) 0.01的平方根是 ( )
(A)0.1 (B)±0.1 (C)0.0001 (D)±0.0001
(2)∵ (0.3)2 = 0.09
∴ ( )
(A)0.09 是 0.3的平方根. (B)0.09是0.3的3倍.
(C)0.3 是0.09 的平方根. (D)0.3不是0.09的平方根.
B
C
随堂练习
1. 判断下列说法是否正确:
(1)-9的平方根是-3 ( )
(2)49的平方根是7 ( )
(3)(-2)2的平方根是±2 ( )
(4)1 的平方根是 1 ( )
(5)-1 是 1的平方根 ( )
(6)7的平方根是±49 ( )
(7)若X2 = 16, 则X = 4 ( )
×
×
√
×
√
×
×
3 有没有平方根 ?
若有 ,怎样表示?
没有,说明为什么 ?
负的平方根表示为:
即m的平方根表示为:
+
-
±
一个数的平方根的表示方法:
±
± =±7
3的平方根是:
±
如:49 的平方根是
则:
非负数m
正的平方根表示为:
(m≥0)
(1)100 (2) (3)0.0001
解:
例1.求下列各数的平方根:
(1)∵( )2 =100,
∴ 100的平方根为±10.
∴ 的平方根为
(2)∵( )2 =
解(3)∵( )2 =0.0001,
∴ 0.0001的平方根为±0.01.
练习:求下列各数的平方根:
(1) 1.69
(1)100 (2) (3)0.0001
例1.求下列各数的平方根:
1.本节课引入了新的运算——开方运算,开方和乘方互为逆运算,从而完备了初等代数中六种基本代数运算(加、减、乘、除、乘方、开方),这对代数内容学习有着重要的意义。
2.本节主要学习了:
①平方根的概念
②平方根的性质:一个正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根
③平方根的表示方法
④求一个数的平方根的运算—开平方,应分清平方运算与开平方运算的区别与联系
小结 & 归纳
下列各数有平方根吗?说明理由。
(1)- 4 ( )
(2)(- 4)2 ( )
(3)- 42 ( )
(4)0 ( )
(5)(-2)3 ( )
(6)|3| ( )
(7) ( )
(8)x2+1 ( )
当这个数为正数时,它有两个平方根;当这个数为0时,它有一个平方根0;当这个数为负数时,它没有平方根。
√
×
×
√
×
√
判断一个数有没有平方根,只要看这个数的符号。
×
√
练习
a
121
196
0.81
104
a的平方根
±11
±14
±0.9
±100
2.填表:
解:∵正数有两个平方根,它们互为相反数。
(1)x的一个平方根是3,则另一个平方根是 ,x= 。
-3
9
(2)3y-22和2y-3是m的两个平方根,试求m的值。
∴ 3y-22+2y-3=0
∴ y=5
∴m=
练习 3
就此别过。
