2020-2021学年人教版数学八年级下册17.1.2利用勾股定理解决简单的实际问题课件(20张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册17.1.2利用勾股定理解决简单的实际问题课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 505.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 00:00:00 | ||
图片预览





文档简介
17.1.2 勾股定理的应用
人教版八年级下册
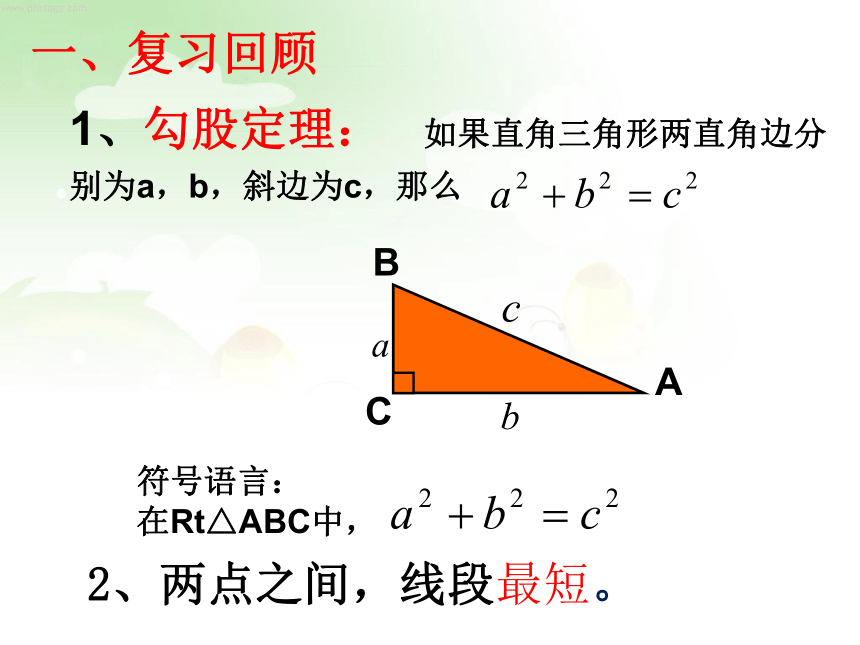
1、勾股定理: 如果直角三角形两直角边分别为a,b,斜边为c,那么
符号语言:
在Rt△ABC中,
A
C
B
一、复习回顾
2、两点之间,线段最短。
1、如图,求出下列直角三角形中未知边的长度。
2、在直角三角形中,若两直角边的长分别为1cm和2cm,则斜边长为______cm。
二、课前热身
3
5
x
x=______
b=______
c=______
13
4
8
3、已知直角三角形中两条边长为3cm和4cm, 则第三条
边的长是_______ cm。
?
4、已知在Rt△ABC中,∠ACB=90°,BC=8,AB=10,CD是斜边AB上的高, 则 CD的长为____________。
4.8
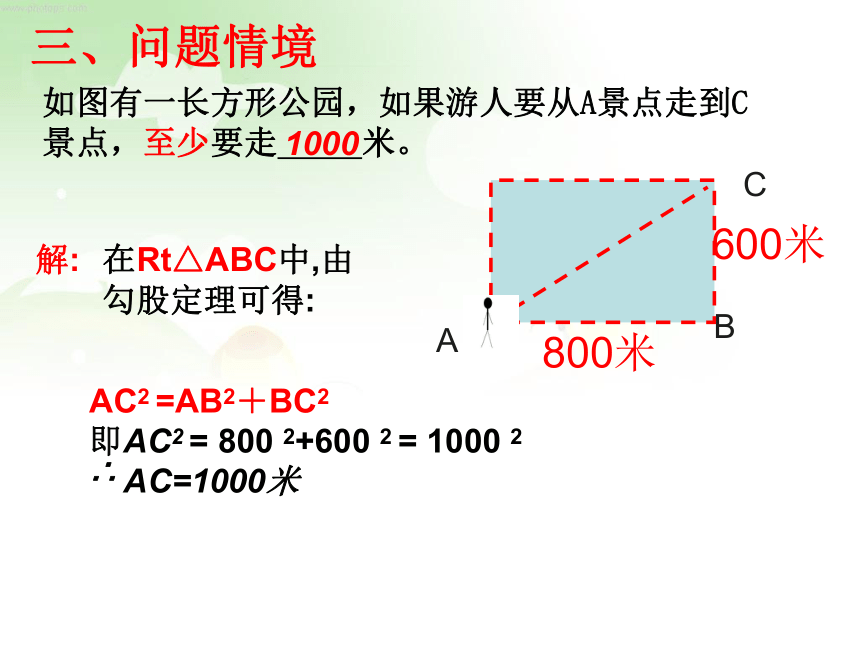
如图有一长方形公园,如果游人要从A景点走到C景点,至少要走 米。
AC2 =AB2+BC2
即AC2 = 800 2+600 2 = 1000 2
∴ AC=1000米
1000
解:
在Rt△ABC中,由勾股定理可得:
A
B
C
800米
600米
三、问题情境
例1: 如图有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少 飞了多少 米 ?
6
8
A
B
C
解: 如图所示,在Rt△ABC中,
由勾股定理可得,
AB2 =AC2+BC2
即AB2 =62 +82= 10 2
∴AB=10米
O
D
6
8
A
B
C
探究一:平面中的最短路径
四、探究新知
求平面图形中的最短路径的关键是:
构造直角三角形,再运用勾股定理求解。
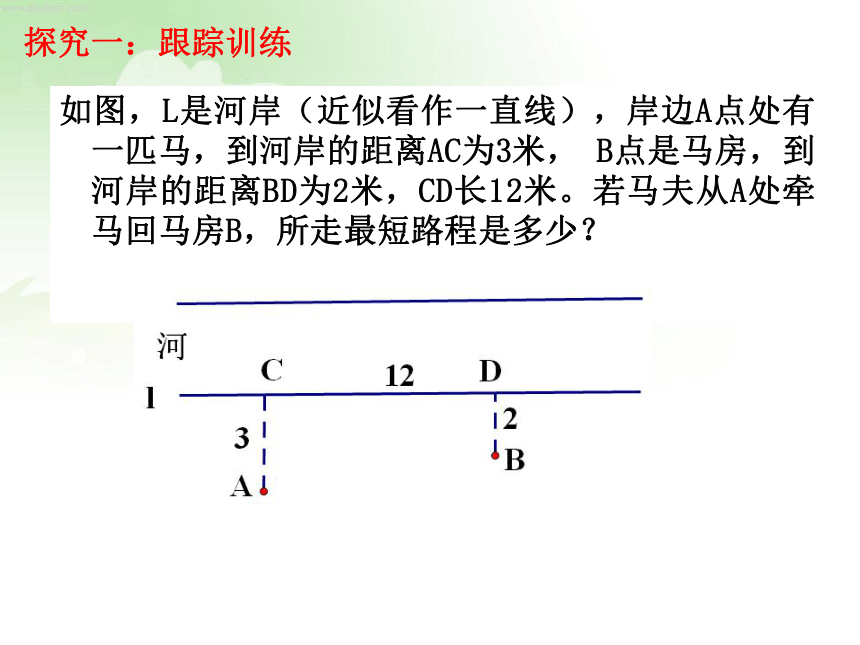
如图,L是河岸(近似看作一直线),岸边A点处有一匹马,到河岸的距离AC为3米, B点是马房,到河岸的距离BD为2米,CD长12米。若马夫从A处牵马回马房B,所走最短路程是多少?
探究一:跟踪训练
B
A
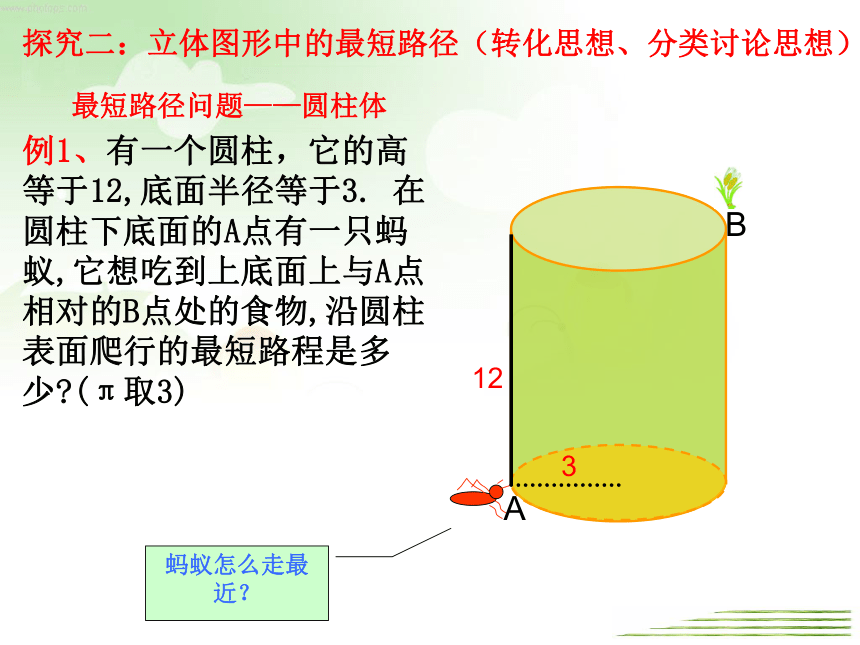
例1、有一个圆柱,它的高等于12,底面半径等于3. 在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,沿圆柱表面爬行的最短路程是多少?(π取3)
12
3
蚂蚁怎么走最近?
探究二:立体图形中的最短路径(转化思想、分类讨论思想)
最短路径问题——圆柱体
1.拿出自己做的圆柱,尝试从A点到B点沿圆柱侧面画出几条路线,你觉得哪条路线最短呢?
2.以小组为单位,研究蚂蚁爬行的路线有几种方案? 分别表示在圆柱上.
3. 找出蚂蚁爬行的最短路线。
B
A
最短路径问题——圆柱体
动手尝试
A
B
A′
B
A
A′
d
12
3
所走路程为高+直径=12+2×3=18
侧面展开图
A
B
A′
所走路程为高 + =12+3×3=21
πr
蚂蚁爬行的最短路程AB的长为 。
15
A
B
A′
B
A
A′
方案二:
方案一:
方案三:
πr
12
最短路径问题——圆柱体
例2、 如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是多少?
A
C
D
B
E
6
4
3
最短路径问题——长方体
怎样展开?
探究三:立体图形中的最短路径(转化思想、分类讨论思想)
A
C
D
B
B
E
6
4
3
展开前面和上面
最短路径问题——长方体
A
C
D
B
E
B
?
?
展开前面和右面
最短路径问题——长方体
6
4
3
A
C
D
B
E
A
展开左面和上面
最短路径问题——长方体
6
4
3
A
C
D
B
E
6
4
3
A
C
D
E
B
6
4
3
C
B
E
A
6
4
3
展开前面和上面
展开前面和右面
展开左面和上面
求立体图形最短路径的关键是:把立体图形展开转化为平面图形,利用两点之间线段最短找到最短路径,然后运用勾股定理求解。
注意:展开面不同,得到的路径也不相同。
最短路径问题——长方体
有一圆形油罐底面圆的周长为24m,高为6m,
一只老鼠从距底面1m的A处爬行到对角B处吃
食物,它爬行的最短路线长为多少米?
探究二:跟踪训练
探究三:跟踪训练
如图:一只蚂蚁从长、宽都是30cm,高是80cm的长方体
纸箱的A点沿纸箱爬到B点,求它爬行的最短路线长是多
少米?
2、体会数形结合思想、转化思想、分类讨论的思想在解决数学问题中的作用。
1、立体图形展开转化为平面图形,利用两点之间线段最短找到最短路径,然后运用勾股定理求解。
(注意:展开面不同,得到的路径也不相同)
五、课堂小结
谢谢!
人教版八年级下册
1、勾股定理: 如果直角三角形两直角边分别为a,b,斜边为c,那么
符号语言:
在Rt△ABC中,
A
C
B
一、复习回顾
2、两点之间,线段最短。
1、如图,求出下列直角三角形中未知边的长度。
2、在直角三角形中,若两直角边的长分别为1cm和2cm,则斜边长为______cm。
二、课前热身
3
5
x
x=______
b=______
c=______
13
4
8
3、已知直角三角形中两条边长为3cm和4cm, 则第三条
边的长是_______ cm。
?
4、已知在Rt△ABC中,∠ACB=90°,BC=8,AB=10,CD是斜边AB上的高, 则 CD的长为____________。
4.8
如图有一长方形公园,如果游人要从A景点走到C景点,至少要走 米。
AC2 =AB2+BC2
即AC2 = 800 2+600 2 = 1000 2
∴ AC=1000米
1000
解:
在Rt△ABC中,由勾股定理可得:
A
B
C
800米
600米
三、问题情境
例1: 如图有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少 飞了多少 米 ?
6
8
A
B
C
解: 如图所示,在Rt△ABC中,
由勾股定理可得,
AB2 =AC2+BC2
即AB2 =62 +82= 10 2
∴AB=10米
O
D
6
8
A
B
C
探究一:平面中的最短路径
四、探究新知
求平面图形中的最短路径的关键是:
构造直角三角形,再运用勾股定理求解。
如图,L是河岸(近似看作一直线),岸边A点处有一匹马,到河岸的距离AC为3米, B点是马房,到河岸的距离BD为2米,CD长12米。若马夫从A处牵马回马房B,所走最短路程是多少?
探究一:跟踪训练
B
A
例1、有一个圆柱,它的高等于12,底面半径等于3. 在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,沿圆柱表面爬行的最短路程是多少?(π取3)
12
3
蚂蚁怎么走最近?
探究二:立体图形中的最短路径(转化思想、分类讨论思想)
最短路径问题——圆柱体
1.拿出自己做的圆柱,尝试从A点到B点沿圆柱侧面画出几条路线,你觉得哪条路线最短呢?
2.以小组为单位,研究蚂蚁爬行的路线有几种方案? 分别表示在圆柱上.
3. 找出蚂蚁爬行的最短路线。
B
A
最短路径问题——圆柱体
动手尝试
A
B
A′
B
A
A′
d
12
3
所走路程为高+直径=12+2×3=18
侧面展开图
A
B
A′
所走路程为高 + =12+3×3=21
πr
蚂蚁爬行的最短路程AB的长为 。
15
A
B
A′
B
A
A′
方案二:
方案一:
方案三:
πr
12
最短路径问题——圆柱体
例2、 如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是多少?
A
C
D
B
E
6
4
3
最短路径问题——长方体
怎样展开?
探究三:立体图形中的最短路径(转化思想、分类讨论思想)
A
C
D
B
B
E
6
4
3
展开前面和上面
最短路径问题——长方体
A
C
D
B
E
B
?
?
展开前面和右面
最短路径问题——长方体
6
4
3
A
C
D
B
E
A
展开左面和上面
最短路径问题——长方体
6
4
3
A
C
D
B
E
6
4
3
A
C
D
E
B
6
4
3
C
B
E
A
6
4
3
展开前面和上面
展开前面和右面
展开左面和上面
求立体图形最短路径的关键是:把立体图形展开转化为平面图形,利用两点之间线段最短找到最短路径,然后运用勾股定理求解。
注意:展开面不同,得到的路径也不相同。
最短路径问题——长方体
有一圆形油罐底面圆的周长为24m,高为6m,
一只老鼠从距底面1m的A处爬行到对角B处吃
食物,它爬行的最短路线长为多少米?
探究二:跟踪训练
探究三:跟踪训练
如图:一只蚂蚁从长、宽都是30cm,高是80cm的长方体
纸箱的A点沿纸箱爬到B点,求它爬行的最短路线长是多
少米?
2、体会数形结合思想、转化思想、分类讨论的思想在解决数学问题中的作用。
1、立体图形展开转化为平面图形,利用两点之间线段最短找到最短路径,然后运用勾股定理求解。
(注意:展开面不同,得到的路径也不相同)
五、课堂小结
谢谢!
