2020-2021学年人教版 八年级数学下册 18.1.1 平行四边形的性质培优训练(Word版 含答案)
文档属性
| 名称 | 2020-2021学年人教版 八年级数学下册 18.1.1 平行四边形的性质培优训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 652.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 23:57:04 | ||
图片预览


文档简介
18.1.1 平行四边形的性质培优训练
一、选择题
1. 以三角形的三个顶点作平行四边形,最多可以作( )
A.2个 B.3个 C.4个 D.5个
2. 如图,在?ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )
A. 1 B. 2 C. 3 D. 4
3. 如图,将?ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
4. 如图,平行四边形ABCD的周长是26 cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3 cm,则AE的长度为( )
A. 3 cm B. 4 cm C. 5 cm D. 8 cm
5. 在平行四边形中,点、、、和、、、分别为和的五等分点,点、和、分别是和的三等分点,已知四边形的面积为,则平行四边形面积为( )
A.2 B. C. D.
6. 如图,ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是
A.EH=HG
B.四边形EFGH是平行四边形
C.AC⊥BD
D.△ABO的面积是△EFO的面积的2倍
7. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为
A.12 B.14 C.24 D.21
8. 如图,点分别在的边上,且
,,有黑、白两只蚂蚁,它们同时同速从点出发,黑蚂蚁沿路线爬行,白蚂蚁沿路线爬行,那么( )
黑蚂蚁先回到点
白蚂蚁先回到点
两只蚂蚁同时回到点
哪只蚂蚁先回到点视各点的位置而定
二、填空题
9. 如图,在平行四边中,,则 .
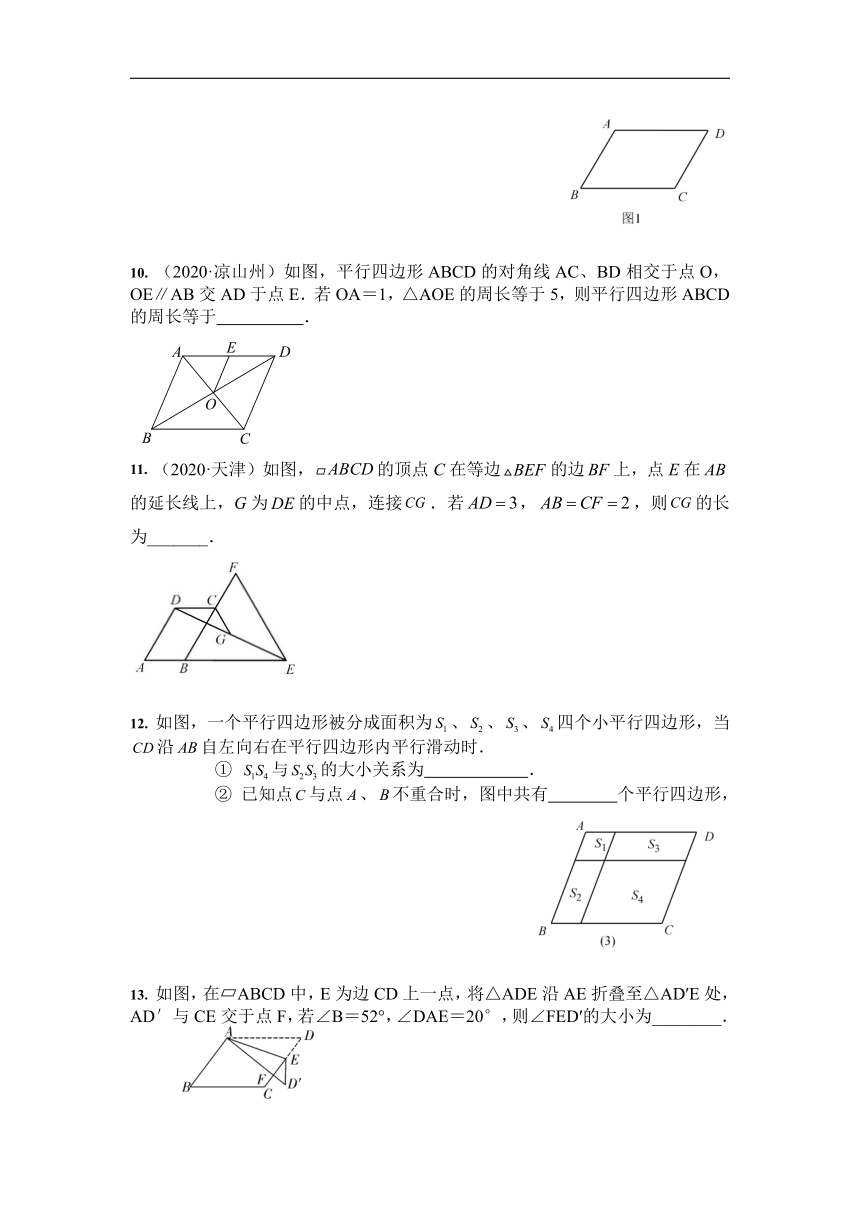
10. (2020·凉山州)如图,平行四边形ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E.若OA=1,△AOE的周长等于5,则平行四边形ABCD的周长等于 .
11. (2020·天津)如图,的顶点C在等边的边上,点E在的延长线上,G为的中点,连接.若,,则的长为_______.
12. 如图,一个平行四边形被分成面积为、、、四个小平行四边形,当沿自左向右在平行四边形内平行滑动时.
① 与的大小关系为 .
② 已知点与点、不重合时,图中共有 个平行四边形,
13. 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为________.
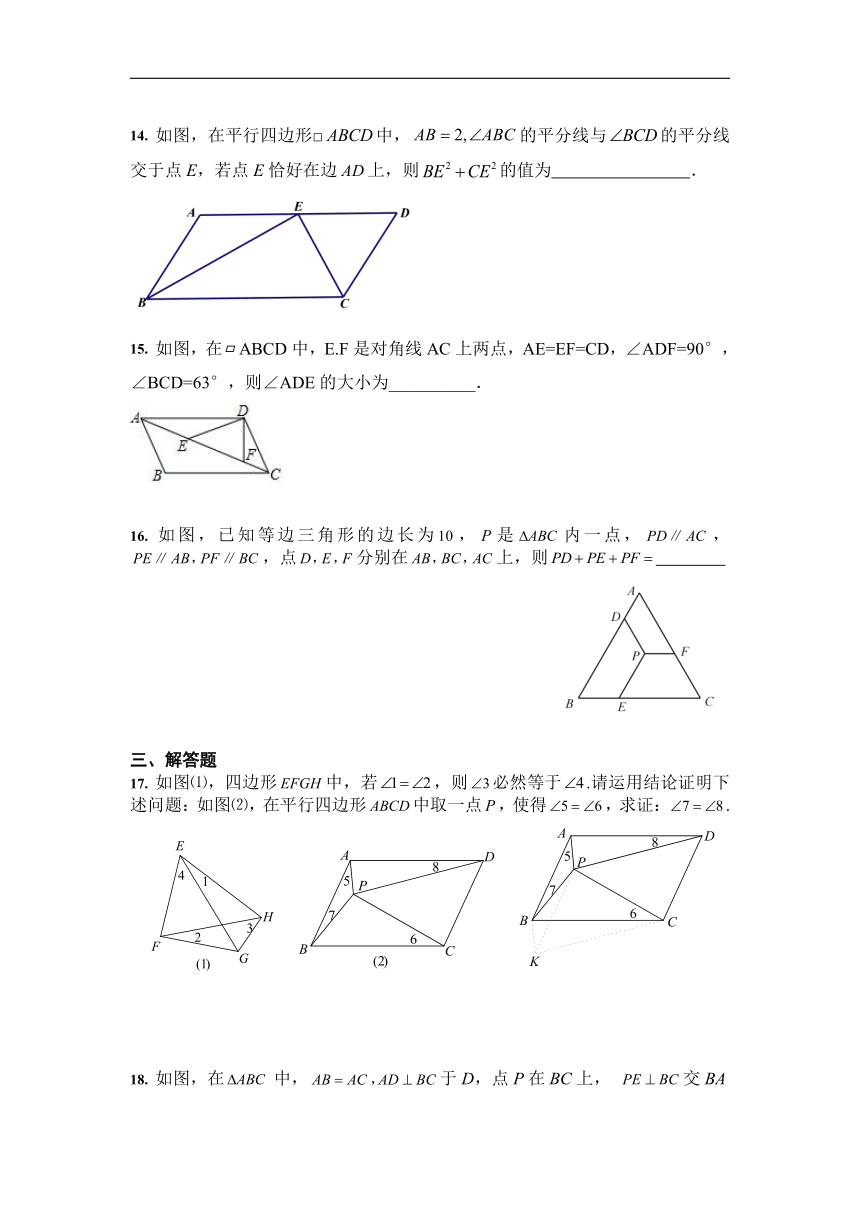
14. 如图,在平行四边形□中,的平分线与的平分线交于点E,若点E恰好在边上,则的值为 .
15. 如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
16. 如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
三、解答题
17. 如图⑴,四边形中,若,则必然等于.请运用结论证明下述问题:如图⑵,在平行四边形中取一点,使得,求证:.
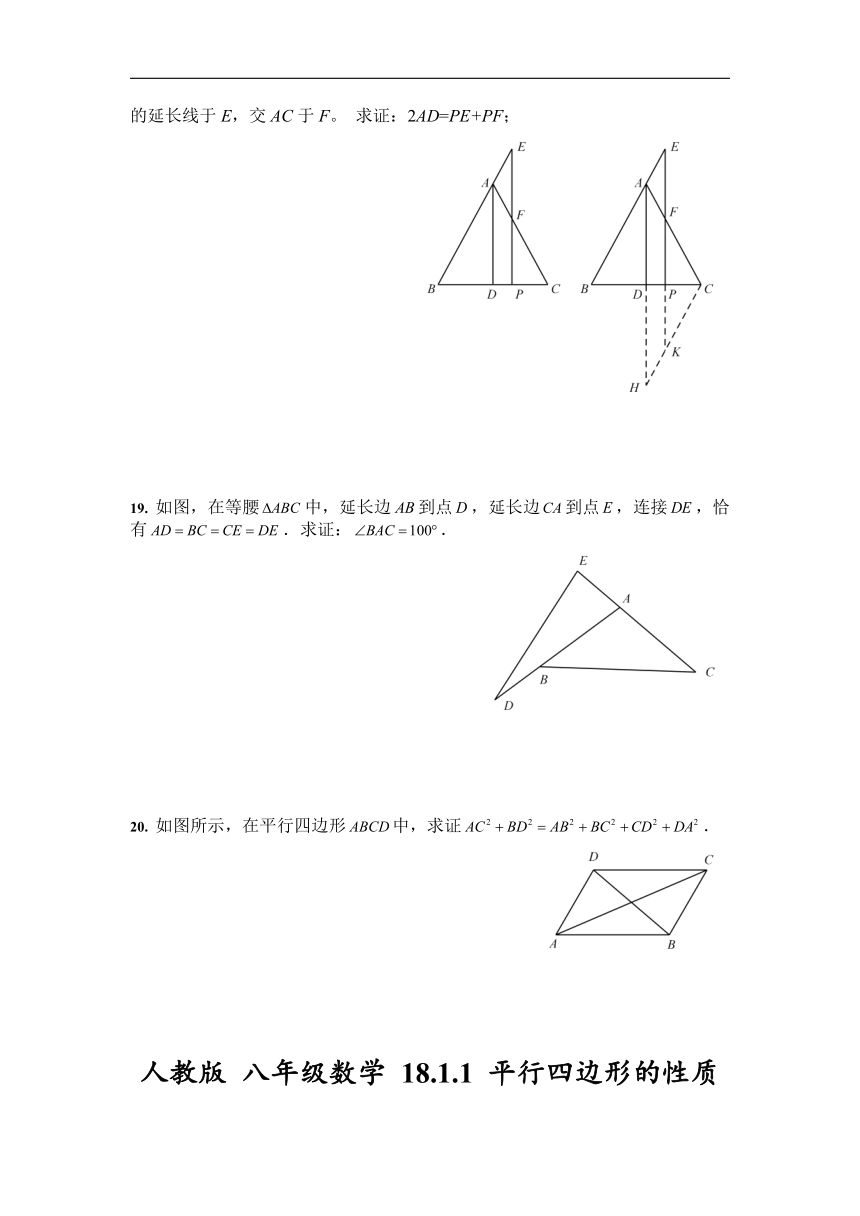
18. 如图,在中,于D,点P在BC上, 交BA的延长线于E,交AC于F。 求证:2AD=PE+PF;
19. 如图,在等腰中,延长边到点,延长边到点,连接,恰有.求证:.
20. 如图所示,在平行四边形中,求证.
人教版 八年级数学 18.1.1 平行四边形的性质 答案
一、选择题
1. 【答案】B
2. 【答案】C 【解析】∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABM=∠CMB,∵BM平分∠ABC,∴∠ABM=∠CBM,∴∠CBM=∠CMB,∴CB=MC=2,∴AD=BC=2,∵?ABCD的周长是14,∴AB=CD=5,∴DM=DC-MC=3.
3. 【答案】C 【解析】设∠ACD =x,∠B=y,则根据题意可列方程组,解得y=114°.
4. 【答案】B 【解析】在?ABCD中,AD=BC,AB=CD,BO=DO,∵平行四边形ABCD的周长为26 cm,∴AB+BC=13 cm,又∵△AOD的周长比△AOB的周长多3 cm,∴AD-AB=BC-AB=3 cm,解得AB=5 cm,BC=8 cm,又AB⊥AC,E是BC的中点,∴AE=BE=CE=BC=4 cm.
5. 【答案】C
6. 【答案】B
【解析】∵E,F,G,H分别是AO,BO,CO,DO的中点,在ABCD中,AB=2,AD=4,
∴EH=AD=2,HG=AB=1,∴EH≠HG,故选项A错误;
∵E,F,G,H分别是AO,BO,CO,DO的中点,
∴EH=,
∴四边形EFGH是平行四边形,故选项B正确;
由题目中的条件,无法判断AC和BD是否垂直,故选项C错误;
∵点E、F分别为OA和OB的中点,
∴EF=,EF∥AB,∴△OEF∽△OAB,∴,
即△ABO的面积是△EFO的面积的4倍,故选项D错误,
故选B.
7. 【答案】A
【解析】∵BD⊥CD,BD=4,CD=3,
∴BC==5,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴EH=FG=BC,EF=GH=AD,
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,
又∵AD=7,
∴四边形EFGH的周长=7+5=12.故选A.
8. 【答案】C
【解析】可知四边形均为平行四边形,可知选C
二、填空题
9. 【答案】
10. 【答案】16
【解析】∵四边形ABCD是平行四边形,∴OA=OC,AB=CD,AD=BC.∵OE∥AB,∴OE是△ACD的中位线.∴AE=AD,OE=CD.∵OA=1,△AOE的周长等于5,∴AE+OE=4.∴AD+CD=8.∴平行四边形ABCD的周长=16.故答案为16.
11. 【答案】
【解析】本题考查了平行四边形的性质、等边三角形的性质、中位线等知识点,延长DC交EF于点M,利用平行四边形、等边三角形性质求出相应的线段长,证出是的中位线是解题的关键.延长DC交EF于点M(图见详解),根据平行四边形与等边三角形的性质,可证△CFM是等边三角形,BF=BE=EF=BC+CF=5,可求出CF=CM=MF=2,可得C、G是DM和DE的中点,根据中位线的性质,可得出CG=,代入数值即可得出答案.如下图所示,延长DC交EF于点M,,,
平行四边形的顶点C在等边的边上,
,
是等边三角形,
.
在平行四边形中,,,
又是等边三角形,
,
.
G为的中点,,
是的中点,且是的中位线,
.
故答案为:.
12. 【答案】①;②
13. 【答案】36° 【解析】∵在?ABCD中,∠D=∠B=52°,∴∠AEF=∠DAE+∠D=20°+52°=72°,∴∠AED=180°-∠AEF=108°,由折叠的性质得,∠AED′=∠AED=108°,∴∠FED′=∠AED′-∠AEF=108°-72°=36°.
14. 【答案】16
【解析】∵四边形ABCD是平行四边形,∴AB=CD=2,AD=BC,AD∥BC,AB∥CD,∴∠ABC+∠BCD=180°, ∠AEB=∠EBC,∠DEC=∠ECB.又∵BE、CE分别是∠ABC与∠DCB的平分线,∴∠ABE=∠EBC,∠DCE=∠ECB,∴∠EBC+∠BCE=90°,∠ABE=∠AEB,∠DCE=∠DEC,∴AB=AE=2,DC=DE=2,
15. 【答案】21°
【解析】设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
16. 【答案】
三、解答题
17. 【答案】
分别过点、作,,交于点,连接.
∵,
∴,,,
∵,,∴,
∴为平行四边形,∴
∵,∴≌,∴
在四边形中,
∴,∴
18. 【答案】
分析:加倍中线构造平行四边形,然后再通过等量线段证明原式成立。
证明:延长AD,使得AD=DH,连接CH,延长FP交CH于点K。
∵
∵
∴为平行四边形
∴
∵为公共边
∴
∴
∵
∴为平行四边形
∴
∴
说明:倍长中线构造平行四边形是竞赛中常用的技巧之一,竞赛班的学生一定要掌握。
而运用其性质的一个典型例题。
19. 【答案】
由,知是等腰三角形,其底角必为钝角,所以等腰中,必为钝角,因此必为等腰的顶角,则、是腰,即.
过作的平行线,与过所作的平行线交于点,则四边形为平行四边形,故,,.
从而,.
连,在和中,
,,
,
则,于是.
而,即知是等边三角形,从而
.
设,则
,
,
.
由,得
.解得,即.
20. 【答案】
本题实质是证明.
如图所示,过点作交的延长线于点,
因为,,
故是平行四边形,从而,.
作,是垂足,则:
,
,
故.
一、选择题
1. 以三角形的三个顶点作平行四边形,最多可以作( )
A.2个 B.3个 C.4个 D.5个
2. 如图,在?ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,?ABCD的周长是14,则DM等于( )
A. 1 B. 2 C. 3 D. 4
3. 如图,将?ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
4. 如图,平行四边形ABCD的周长是26 cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3 cm,则AE的长度为( )
A. 3 cm B. 4 cm C. 5 cm D. 8 cm
5. 在平行四边形中,点、、、和、、、分别为和的五等分点,点、和、分别是和的三等分点,已知四边形的面积为,则平行四边形面积为( )
A.2 B. C. D.
6. 如图,ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是
A.EH=HG
B.四边形EFGH是平行四边形
C.AC⊥BD
D.△ABO的面积是△EFO的面积的2倍
7. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为
A.12 B.14 C.24 D.21
8. 如图,点分别在的边上,且
,,有黑、白两只蚂蚁,它们同时同速从点出发,黑蚂蚁沿路线爬行,白蚂蚁沿路线爬行,那么( )
黑蚂蚁先回到点
白蚂蚁先回到点
两只蚂蚁同时回到点
哪只蚂蚁先回到点视各点的位置而定
二、填空题
9. 如图,在平行四边中,,则 .
10. (2020·凉山州)如图,平行四边形ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E.若OA=1,△AOE的周长等于5,则平行四边形ABCD的周长等于 .
11. (2020·天津)如图,的顶点C在等边的边上,点E在的延长线上,G为的中点,连接.若,,则的长为_______.
12. 如图,一个平行四边形被分成面积为、、、四个小平行四边形,当沿自左向右在平行四边形内平行滑动时.
① 与的大小关系为 .
② 已知点与点、不重合时,图中共有 个平行四边形,
13. 如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为________.
14. 如图,在平行四边形□中,的平分线与的平分线交于点E,若点E恰好在边上,则的值为 .
15. 如图,在ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为__________.
16. 如图,已知等边三角形的边长为,是内一点,,,点分别在上,则
三、解答题
17. 如图⑴,四边形中,若,则必然等于.请运用结论证明下述问题:如图⑵,在平行四边形中取一点,使得,求证:.
18. 如图,在中,于D,点P在BC上, 交BA的延长线于E,交AC于F。 求证:2AD=PE+PF;
19. 如图,在等腰中,延长边到点,延长边到点,连接,恰有.求证:.
20. 如图所示,在平行四边形中,求证.
人教版 八年级数学 18.1.1 平行四边形的性质 答案
一、选择题
1. 【答案】B
2. 【答案】C 【解析】∵四边形ABCD是平行四边形,∴AB∥CD,∴∠ABM=∠CMB,∵BM平分∠ABC,∴∠ABM=∠CBM,∴∠CBM=∠CMB,∴CB=MC=2,∴AD=BC=2,∵?ABCD的周长是14,∴AB=CD=5,∴DM=DC-MC=3.
3. 【答案】C 【解析】设∠ACD =x,∠B=y,则根据题意可列方程组,解得y=114°.
4. 【答案】B 【解析】在?ABCD中,AD=BC,AB=CD,BO=DO,∵平行四边形ABCD的周长为26 cm,∴AB+BC=13 cm,又∵△AOD的周长比△AOB的周长多3 cm,∴AD-AB=BC-AB=3 cm,解得AB=5 cm,BC=8 cm,又AB⊥AC,E是BC的中点,∴AE=BE=CE=BC=4 cm.
5. 【答案】C
6. 【答案】B
【解析】∵E,F,G,H分别是AO,BO,CO,DO的中点,在ABCD中,AB=2,AD=4,
∴EH=AD=2,HG=AB=1,∴EH≠HG,故选项A错误;
∵E,F,G,H分别是AO,BO,CO,DO的中点,
∴EH=,
∴四边形EFGH是平行四边形,故选项B正确;
由题目中的条件,无法判断AC和BD是否垂直,故选项C错误;
∵点E、F分别为OA和OB的中点,
∴EF=,EF∥AB,∴△OEF∽△OAB,∴,
即△ABO的面积是△EFO的面积的4倍,故选项D错误,
故选B.
7. 【答案】A
【解析】∵BD⊥CD,BD=4,CD=3,
∴BC==5,
∵E、F、G、H分别是AB、AC、CD、BD的中点,
∴EH=FG=BC,EF=GH=AD,
∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,
又∵AD=7,
∴四边形EFGH的周长=7+5=12.故选A.
8. 【答案】C
【解析】可知四边形均为平行四边形,可知选C
二、填空题
9. 【答案】
10. 【答案】16
【解析】∵四边形ABCD是平行四边形,∴OA=OC,AB=CD,AD=BC.∵OE∥AB,∴OE是△ACD的中位线.∴AE=AD,OE=CD.∵OA=1,△AOE的周长等于5,∴AE+OE=4.∴AD+CD=8.∴平行四边形ABCD的周长=16.故答案为16.
11. 【答案】
【解析】本题考查了平行四边形的性质、等边三角形的性质、中位线等知识点,延长DC交EF于点M,利用平行四边形、等边三角形性质求出相应的线段长,证出是的中位线是解题的关键.延长DC交EF于点M(图见详解),根据平行四边形与等边三角形的性质,可证△CFM是等边三角形,BF=BE=EF=BC+CF=5,可求出CF=CM=MF=2,可得C、G是DM和DE的中点,根据中位线的性质,可得出CG=,代入数值即可得出答案.如下图所示,延长DC交EF于点M,,,
平行四边形的顶点C在等边的边上,
,
是等边三角形,
.
在平行四边形中,,,
又是等边三角形,
,
.
G为的中点,,
是的中点,且是的中位线,
.
故答案为:.
12. 【答案】①;②
13. 【答案】36° 【解析】∵在?ABCD中,∠D=∠B=52°,∴∠AEF=∠DAE+∠D=20°+52°=72°,∴∠AED=180°-∠AEF=108°,由折叠的性质得,∠AED′=∠AED=108°,∴∠FED′=∠AED′-∠AEF=108°-72°=36°.
14. 【答案】16
【解析】∵四边形ABCD是平行四边形,∴AB=CD=2,AD=BC,AD∥BC,AB∥CD,∴∠ABC+∠BCD=180°, ∠AEB=∠EBC,∠DEC=∠ECB.又∵BE、CE分别是∠ABC与∠DCB的平分线,∴∠ABE=∠EBC,∠DCE=∠ECB,∴∠EBC+∠BCE=90°,∠ABE=∠AEB,∠DCE=∠DEC,∴AB=AE=2,DC=DE=2,
15. 【答案】21°
【解析】设∠ADE=x,
∵AE=EF,∠ADF=90°,
∴∠DAE=∠ADE=x,DE=AF=AE=EF,
∵AE=EF=CD,∴DE=CD,
∴∠DCE=∠DEC=2x,
∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠BCA=x,
∴∠DCE=∠BCD﹣∠BCA=63°﹣x,
∴2x=63°﹣x,解得x=21°,即∠ADE=21°;
故答案为:21°.
16. 【答案】
三、解答题
17. 【答案】
分别过点、作,,交于点,连接.
∵,
∴,,,
∵,,∴,
∴为平行四边形,∴
∵,∴≌,∴
在四边形中,
∴,∴
18. 【答案】
分析:加倍中线构造平行四边形,然后再通过等量线段证明原式成立。
证明:延长AD,使得AD=DH,连接CH,延长FP交CH于点K。
∵
∵
∴为平行四边形
∴
∵为公共边
∴
∴
∵
∴为平行四边形
∴
∴
说明:倍长中线构造平行四边形是竞赛中常用的技巧之一,竞赛班的学生一定要掌握。
而运用其性质的一个典型例题。
19. 【答案】
由,知是等腰三角形,其底角必为钝角,所以等腰中,必为钝角,因此必为等腰的顶角,则、是腰,即.
过作的平行线,与过所作的平行线交于点,则四边形为平行四边形,故,,.
从而,.
连,在和中,
,,
,
则,于是.
而,即知是等边三角形,从而
.
设,则
,
,
.
由,得
.解得,即.
20. 【答案】
本题实质是证明.
如图所示,过点作交的延长线于点,
因为,,
故是平行四边形,从而,.
作,是垂足,则:
,
,
故.
