2020-2021学年人教版八年级数学下册课件:18.2.2菱形的性质 第1课时(25张PPT)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册课件:18.2.2菱形的性质 第1课时(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览




文档简介
第十八章 平行四边形
第1课时 菱形的性质
学习目标
1.能说出菱形的定义和性质.
2.能运用菱形的性质定理进行简单的计算与证明.
重点:菱形的性质.
难点:菱形性质的运用.
从生活中认识菱形
追问:你能画出一个菱形吗?
新课导入
我们已经学习了特殊的平行四边形——矩形,它是从哪个角度特殊化来进行研究的?
角的特殊化
特殊化
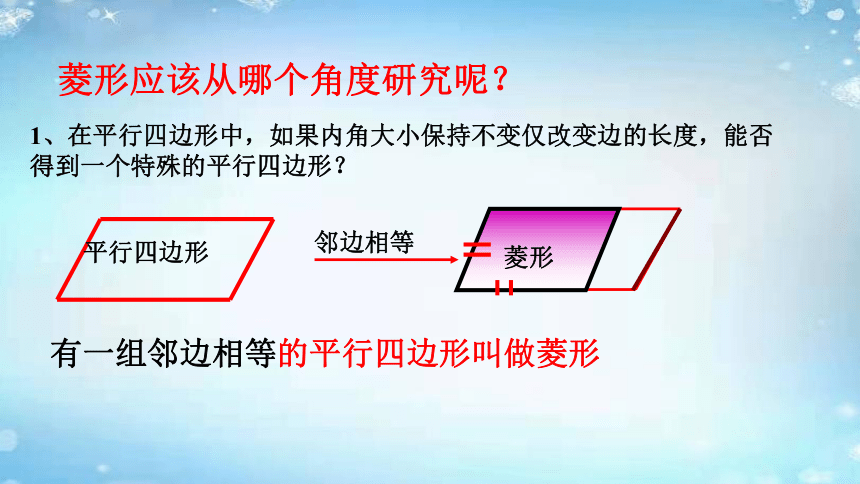
1、在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
平行四边形
有一组邻边相等的平行四边形叫做菱形
菱形
邻边相等
菱形应该从哪个角度研究呢?
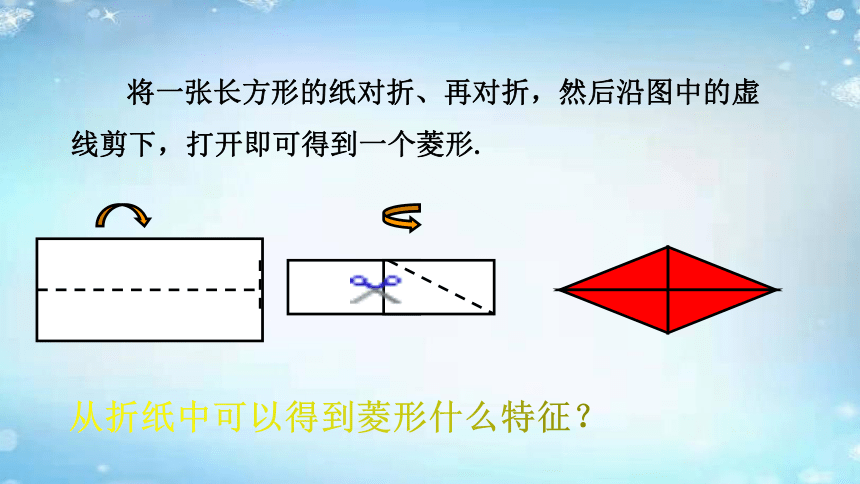
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可得到一个菱形.
从折纸中可以得到菱形什么特征?
画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:
1、菱形是轴对称图形吗?
2、菱形有几条对称轴?
3、对称轴之间有什么关系?
4、你能看出图中哪些线段和角相等?
动手体会谈谈你的发现
相等的线段:
相等的角:
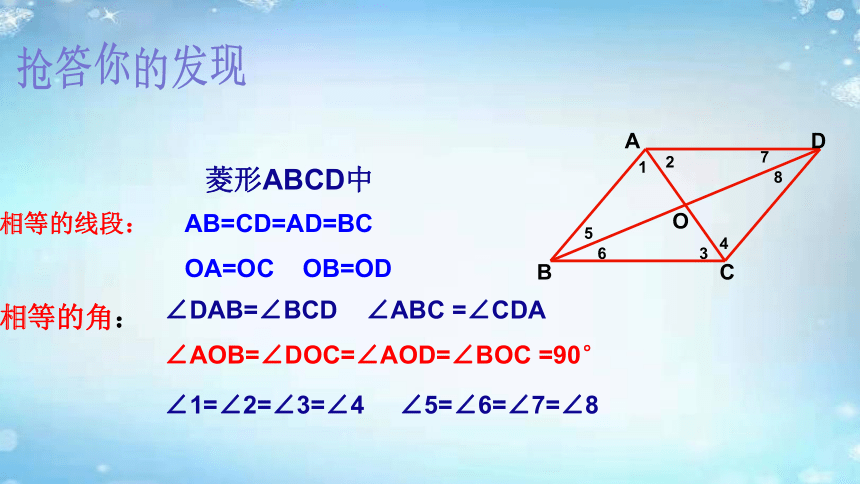
菱形ABCD中
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
A
B
C
D
O
1
2
3
4
5
6
7
8
抢答你的发现
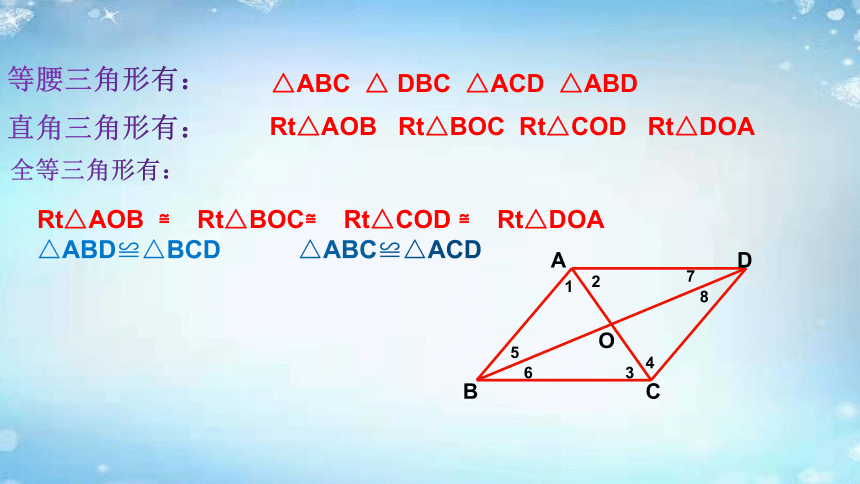
等腰三角形有:
直角三角形有:
全等三角形有:
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
2.菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
1.菱形的四条边相等
3.菱形是轴对称图形,也是中心对称图形
猜想菱形特征
求证:菱形的四条边相等
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。
C
D
B
O
证明猜想
文字表达:
A
A
C
D
B
O
已知:如图四边形ABCD是菱形
(1)AB=BC=CD=DA
(2)AC⊥BD
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
求证:
几何形式
A
C
D
B
O
证明(1)∵四边形ABCD是菱形
∴DA=DC(菱形的定义)
∵DA=BC,AB=DC
∴AB=BC=DC=DA
(2)在△DAC中,又∵AO=CO
∴DB⊥AC,
DB平分∠ADC(三线合一)
同理: DB平分∠ABC;
AC平分∠DAB和∠DCB
菱形具有平行四边形的一切性质;
菱形的四条边都相等;
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;
归纳总结菱形的性质
菱形特有的性质:
你能由两条对角线的长度
求出它的面积吗?
A
C
D
B
O
∵Rt△AOB≌Rt△BOC≌Rt△COD≌Rt△DOA
∴
S
△ABC
=4× OA·OB
菱形ABCD
=4
S
=
AC·BD
1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为____________.
60°和120°
随堂练习
2.如图,菱形ABCD的对角线AC,BD的长分别为6,8,则这个菱形的周长为( )
A.20 B.24 C.40 D.48
A
3.菱形不具备的性质是( )
A.四条边都相等 B.对角线一定相等
C.是轴对称图形 D.是中心对称图形
B
4. 四边形ABCD是菱形,对角线AC、BD相交于点O,
且AB=5,AO=4.
求AC和BD的长.
O
解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD, AC⊥BD.
∵Rt△AOB中,OB2+OA2=AB2,
AB=5cm,AO=4cm,
∴OB=3cm.
∴BD=2OB=6cm, AC=2OA=8cm.
O
5.菱形ABCD的两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积.
C
B
D
A
O
C
B
D
A
O
6 如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
A
B
C
D
O
∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO= ∠ABC= ×60°= 30°.
在Rt△OAB中,AO= AB= ×20=10,
菱形的两条对角线
BO= = = 10
∴花坛的两条小路长 AC=2AO=20(m),
BD=2BO= 20 ≈ 34.64(m).
花坛的面积 S菱形ABCD =4×S△ OAB
= AC·BD=200 ≈346.4(m2).
A
B
C
D
O
解:
1个定义
2个公式
3个特性
:有一组邻边相等的平行四边形叫菱形
:S菱形=底×高
S菱形= 对角线乘积的一半
:特在“边、对角线、对称性”
知识归纳
谢谢观看
第1课时 菱形的性质
学习目标
1.能说出菱形的定义和性质.
2.能运用菱形的性质定理进行简单的计算与证明.
重点:菱形的性质.
难点:菱形性质的运用.
从生活中认识菱形
追问:你能画出一个菱形吗?
新课导入
我们已经学习了特殊的平行四边形——矩形,它是从哪个角度特殊化来进行研究的?
角的特殊化
特殊化
1、在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形?
平行四边形
有一组邻边相等的平行四边形叫做菱形
菱形
邻边相等
菱形应该从哪个角度研究呢?
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可得到一个菱形.
从折纸中可以得到菱形什么特征?
画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:
1、菱形是轴对称图形吗?
2、菱形有几条对称轴?
3、对称轴之间有什么关系?
4、你能看出图中哪些线段和角相等?
动手体会谈谈你的发现
相等的线段:
相等的角:
菱形ABCD中
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
A
B
C
D
O
1
2
3
4
5
6
7
8
抢答你的发现
等腰三角形有:
直角三角形有:
全等三角形有:
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
2.菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
1.菱形的四条边相等
3.菱形是轴对称图形,也是中心对称图形
猜想菱形特征
求证:菱形的四条边相等
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。
C
D
B
O
证明猜想
文字表达:
A
A
C
D
B
O
已知:如图四边形ABCD是菱形
(1)AB=BC=CD=DA
(2)AC⊥BD
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
求证:
几何形式
A
C
D
B
O
证明(1)∵四边形ABCD是菱形
∴DA=DC(菱形的定义)
∵DA=BC,AB=DC
∴AB=BC=DC=DA
(2)在△DAC中,又∵AO=CO
∴DB⊥AC,
DB平分∠ADC(三线合一)
同理: DB平分∠ABC;
AC平分∠DAB和∠DCB
菱形具有平行四边形的一切性质;
菱形的四条边都相等;
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角;
归纳总结菱形的性质
菱形特有的性质:
你能由两条对角线的长度
求出它的面积吗?
A
C
D
B
O
∵Rt△AOB≌Rt△BOC≌Rt△COD≌Rt△DOA
∴
S
△ABC
=4× OA·OB
菱形ABCD
=4
S
=
AC·BD
1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为____________.
60°和120°
随堂练习
2.如图,菱形ABCD的对角线AC,BD的长分别为6,8,则这个菱形的周长为( )
A.20 B.24 C.40 D.48
A
3.菱形不具备的性质是( )
A.四条边都相等 B.对角线一定相等
C.是轴对称图形 D.是中心对称图形
B
4. 四边形ABCD是菱形,对角线AC、BD相交于点O,
且AB=5,AO=4.
求AC和BD的长.
O
解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD, AC⊥BD.
∵Rt△AOB中,OB2+OA2=AB2,
AB=5cm,AO=4cm,
∴OB=3cm.
∴BD=2OB=6cm, AC=2OA=8cm.
O
5.菱形ABCD的两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积.
C
B
D
A
O
C
B
D
A
O
6 如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
A
B
C
D
O
∵花坛ABCD的形状是菱形,
∴AC⊥BD,∠ABO= ∠ABC= ×60°= 30°.
在Rt△OAB中,AO= AB= ×20=10,
菱形的两条对角线
BO= = = 10
∴花坛的两条小路长 AC=2AO=20(m),
BD=2BO= 20 ≈ 34.64(m).
花坛的面积 S菱形ABCD =4×S△ OAB
= AC·BD=200 ≈346.4(m2).
A
B
C
D
O
解:
1个定义
2个公式
3个特性
:有一组邻边相等的平行四边形叫菱形
:S菱形=底×高
S菱形= 对角线乘积的一半
:特在“边、对角线、对称性”
知识归纳
谢谢观看
