2020-2021学年人教版八年级数学下册:18.1.2平行四边形判定 第1课时 课件 (24张PPT)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册:18.1.2平行四边形判定 第1课时 课件 (24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 355.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 07:42:42 | ||
图片预览





文档简介
第1课时 平行四边形的判定
第十八章平行四边形
学习目标
学习重、难点
1.初步掌握平行四边形的定义和2种判定方法及推理格式.
2.能用这些判定方法证明一个四边形是平行四边形.
重点:平行四边形的判定的归纳与论证.
难点:平行四边形的判定的应用及规范表述.
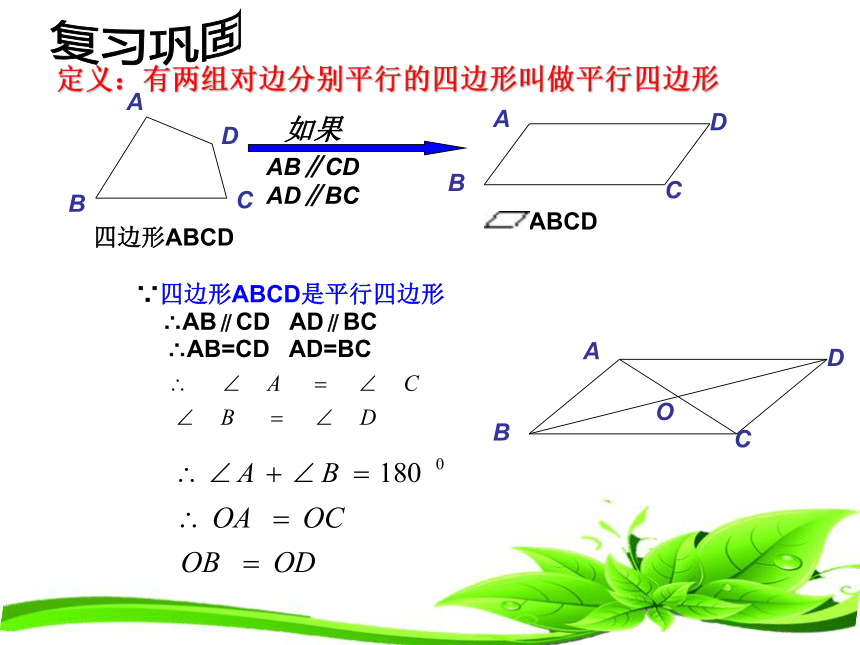
定义:有两组对边分别平行的四边形叫做平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
∵四边形ABCD是平行四边形
复习巩固
∴AB∥CD AD∥BC
∴AB=CD AD=BC
平
行
四
边
形
的
性
质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
探索新知
有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?
D
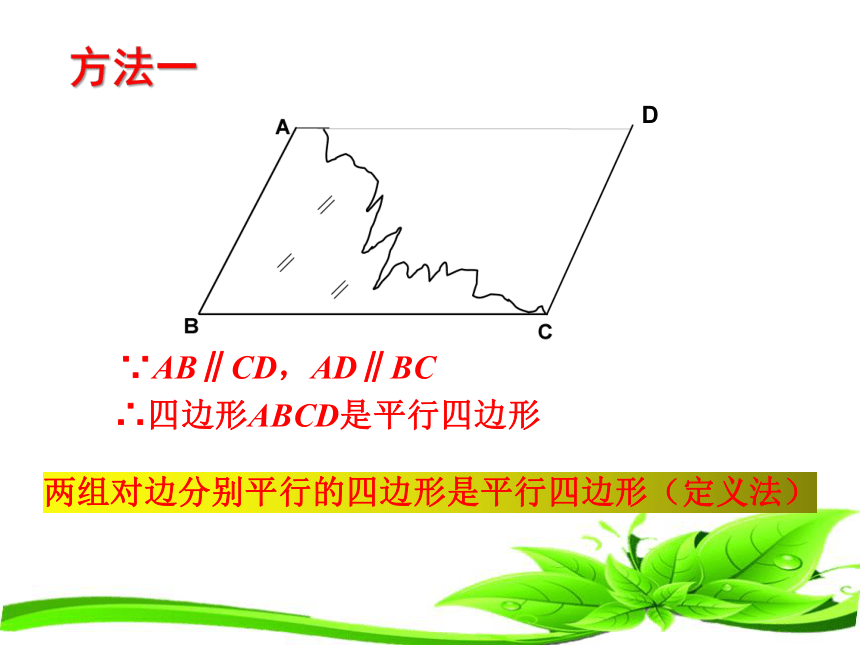
两组对边分别平行的四边形是平行四边形(定义法)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
方法一
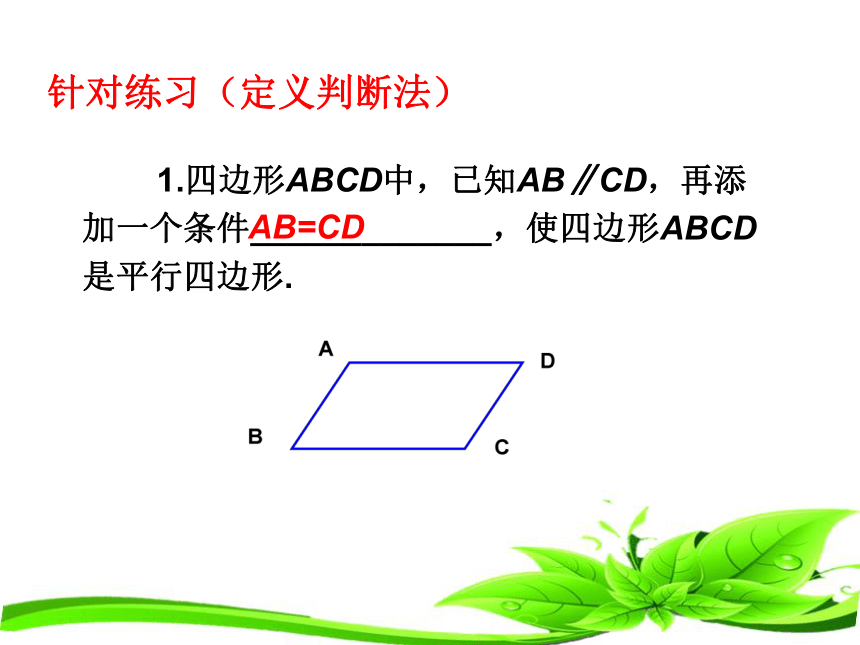
1.四边形ABCD中,已知AB∥CD,再添加一个条件_____________,使四边形ABCD是平行四边形.
AB=CD
针对练习(定义判断法)
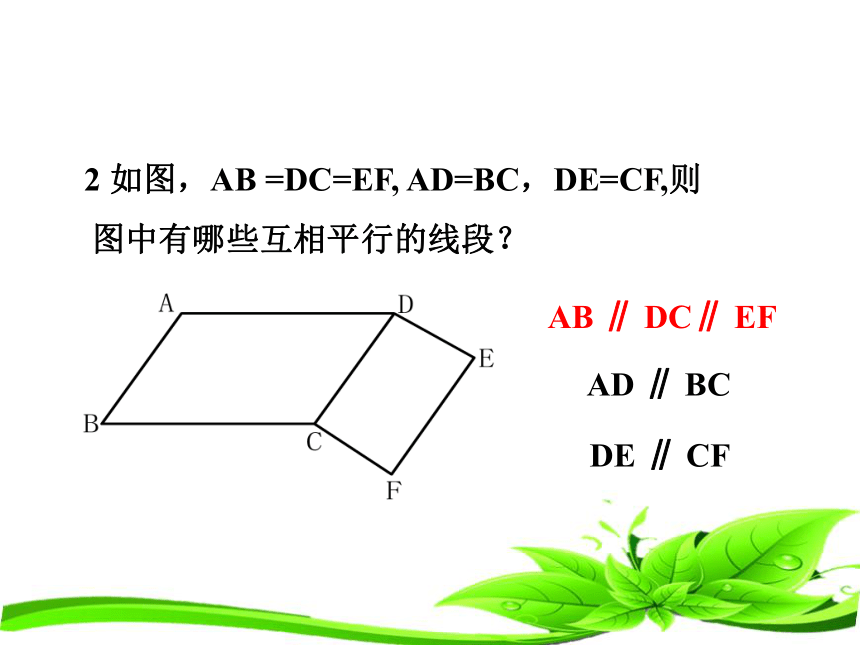
2 如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
D
两组对边分别相等的四边形是平行四边形?
方法二
猜想:
如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.
D
B
A
C
方法二证明
证明:
连结AC
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4
∴四边形ABCD是平行四边形
D
B
A
C
2
1
3
4
两组对边分别相等的四边形是平行四边形.
判定定理1
平行四边形的判定定理1:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
几何语言:
2.如图,在 ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.求证:四边形AFCE是平行四边形.
针对判断1练习
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴AED≌△CBF,
∴AE=CF,在△AEF与△CFE中,AE=CF,
EF=FE,∠AEF=∠CFE=90°,
∴△AEF≌△CFE,∴AE=CF,AF=CE,
∴四边形AFCE是平行四边形.
方法三
D
一组对边平行且相等的四边形是平行四边形?
猜想:
如图,在四边形ABCD中,AB∥CD,AB=CD. 求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD,∴∠1=∠2.
又AB=CD,AC=CA,
∴△ABC≌△CDA. ∴BC=DA.
∴四边形ABCD的两组对边分别相等,它是平行四边形.
方法三证明
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理2:
判定定理2:
几何语言:
∵AB CD
∴四边形ABCD是平行四边形
如图,在 ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
针对判断2练习
证明:∵四边形ABCD是平行四边形,
∴AB=CD,EB∥FD.
又EB= AB,FD= CD,
∴EB=FD.
∴四边形EBFD是平行四边形.
如图, ABCD中,线段EF、GH分别在AB、CD上运动,在运动过程中总是保持EF=GH.
(1)试猜想四边形EFGH的形状,并说明理由.
(2)若EF= AB,且S ABCD=24,
则S四边形EFGH=____.
能力提升
(1)四边形EFGH为平行四边形理由如下:
解:四边形EFGH为平行四边形.
由平行四边形的性质得:AB∥CD,即EF∥GH,又∵EF=GH,
∴四边形EFGH为平行四边形.
(2)若EF= AB,且S ABCD=24,
则S四边形EFGH=____.
8
本节小结
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形.
平行四边形的判定定理:
(定义判断)
谢谢观看
第十八章平行四边形
学习目标
学习重、难点
1.初步掌握平行四边形的定义和2种判定方法及推理格式.
2.能用这些判定方法证明一个四边形是平行四边形.
重点:平行四边形的判定的归纳与论证.
难点:平行四边形的判定的应用及规范表述.
定义:有两组对边分别平行的四边形叫做平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD AD∥BC
B
D
ABCD
A
C
B
D
A
C
O
∵四边形ABCD是平行四边形
复习巩固
∴AB∥CD AD∥BC
∴AB=CD AD=BC
平
行
四
边
形
的
性
质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
探索新知
有一块平行四边形的玻璃块,假如不小心碰碎了一部分,聪明的技师拿着细绳很快将原来的平行四边形画了出来,你知道他用的是什么方法吗?
D
两组对边分别平行的四边形是平行四边形(定义法)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
方法一
1.四边形ABCD中,已知AB∥CD,再添加一个条件_____________,使四边形ABCD是平行四边形.
AB=CD
针对练习(定义判断法)
2 如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
D
两组对边分别相等的四边形是平行四边形?
方法二
猜想:
如图,在四边形ABCD中,AB=CD,AD=BC.求证:四边形ABCD是平行四边形.
D
B
A
C
方法二证明
证明:
连结AC
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4
∴四边形ABCD是平行四边形
D
B
A
C
2
1
3
4
两组对边分别相等的四边形是平行四边形.
判定定理1
平行四边形的判定定理1:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
几何语言:
2.如图,在 ABCD中,BD是它的一条对角线,过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.求证:四边形AFCE是平行四边形.
针对判断1练习
证明:∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,∴∠ADE=∠CBF,
又∠AED=∠CFB=90°,∴AED≌△CBF,
∴AE=CF,在△AEF与△CFE中,AE=CF,
EF=FE,∠AEF=∠CFE=90°,
∴△AEF≌△CFE,∴AE=CF,AF=CE,
∴四边形AFCE是平行四边形.
方法三
D
一组对边平行且相等的四边形是平行四边形?
猜想:
如图,在四边形ABCD中,AB∥CD,AB=CD. 求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD,∴∠1=∠2.
又AB=CD,AC=CA,
∴△ABC≌△CDA. ∴BC=DA.
∴四边形ABCD的两组对边分别相等,它是平行四边形.
方法三证明
一组对边平行且相等的四边形是平行四边形
平行四边形的判定定理2:
判定定理2:
几何语言:
∵AB CD
∴四边形ABCD是平行四边形
如图,在 ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
针对判断2练习
证明:∵四边形ABCD是平行四边形,
∴AB=CD,EB∥FD.
又EB= AB,FD= CD,
∴EB=FD.
∴四边形EBFD是平行四边形.
如图, ABCD中,线段EF、GH分别在AB、CD上运动,在运动过程中总是保持EF=GH.
(1)试猜想四边形EFGH的形状,并说明理由.
(2)若EF= AB,且S ABCD=24,
则S四边形EFGH=____.
能力提升
(1)四边形EFGH为平行四边形理由如下:
解:四边形EFGH为平行四边形.
由平行四边形的性质得:AB∥CD,即EF∥GH,又∵EF=GH,
∴四边形EFGH为平行四边形.
(2)若EF= AB,且S ABCD=24,
则S四边形EFGH=____.
8
本节小结
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形.
平行四边形的判定定理:
(定义判断)
谢谢观看
