2020-2021学年人教版八年级数学下册:18.1.1平行四边形性质 第2课时 课件(25张PPT)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册:18.1.1平行四边形性质 第2课时 课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 401.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 07:40:56 | ||
图片预览




文档简介
第十八章
平行四边形
第2课时
平行四边形的对角线的特征
学习目标
学习重、难点
1.
知道平行四边形的对角线互相平分的性质.
2.能运用这一性质进行推理与计算.
重点:性质的探究.
难点:性质的灵活运用.
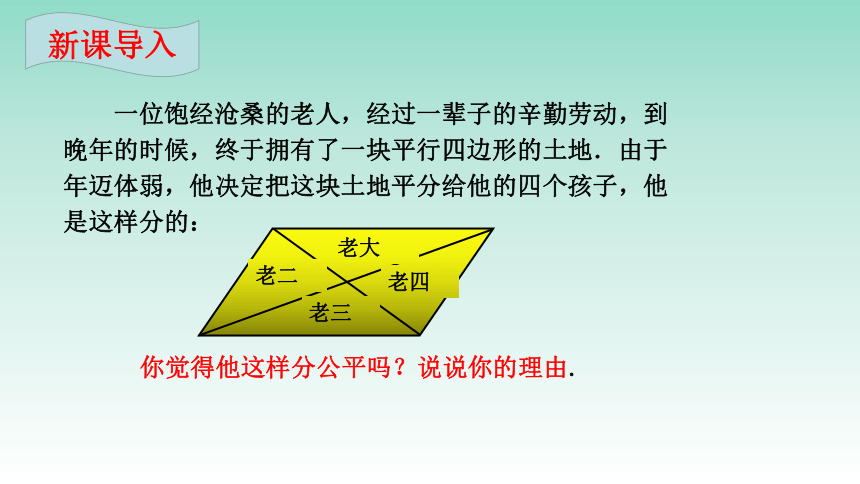
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到
晚年的时候,终于拥有了一块平行四边形的土地.由于
年迈体弱,他决定把这块土地平分给他的四个孩子,他
是这样分的:
老大
老二
老三
老四
你觉得他这样分公平吗?说说你的理由.
新课导入
定义:
性质:
两组对边分别平行的四边形叫做
平
行
四边形。
1.平行四边形的两组对边分别平行;
2.平行四边形的对边相等,
3.平行四边形的对角相等,
相邻两角互补。
A
B
C
D
O
复习回顾
A
B
D
C
O
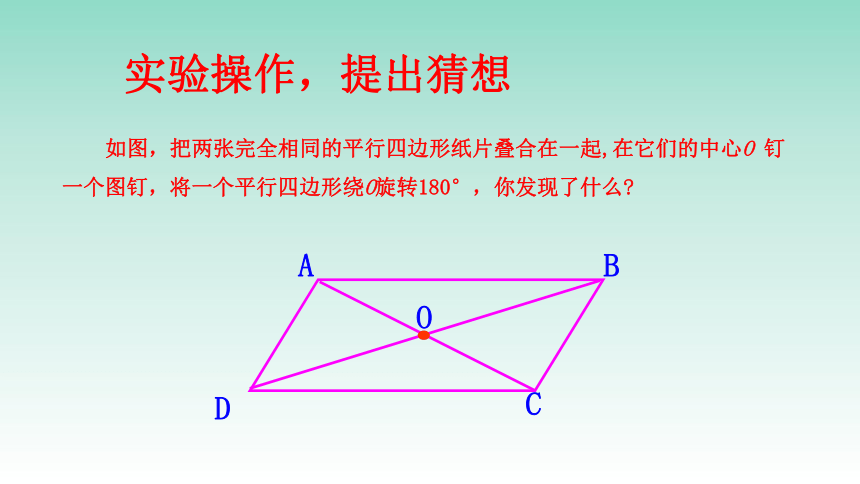
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O
钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
实验操作,提出猜想
●
A
D
O
C
B
D
B
O
C
A
演示
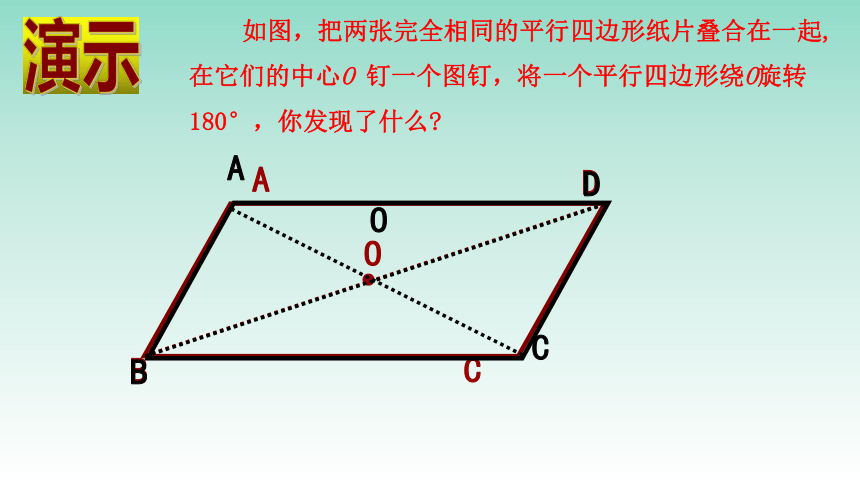
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O
钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
结论:
ABCD绕它的中心O旋转180°后与自身重合,这时我们说
ABCD是中心对称图形点O叫对称中心
有上面的操作演示:
猜想:平行四边形的对角线互相平分.
你能证明上述猜想吗?
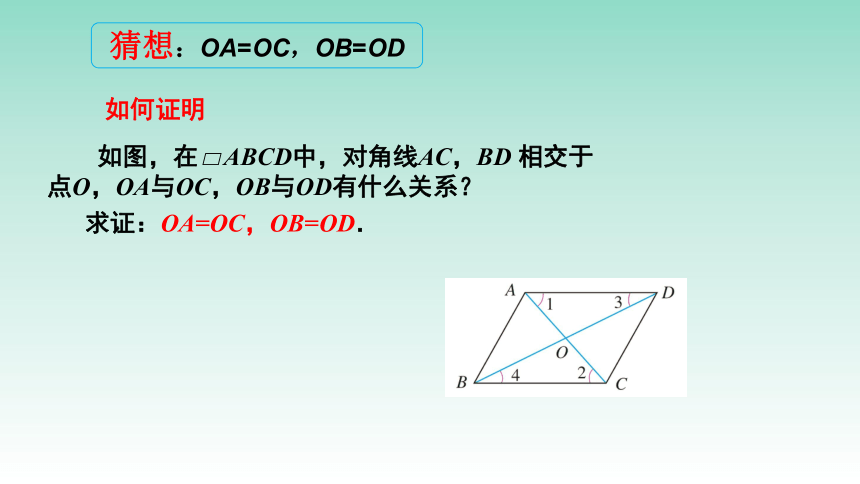
猜想:OA=OC,OB=OD
如何证明
如图,在 ABCD中,对角线AC,BD
相交于点O,OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD.
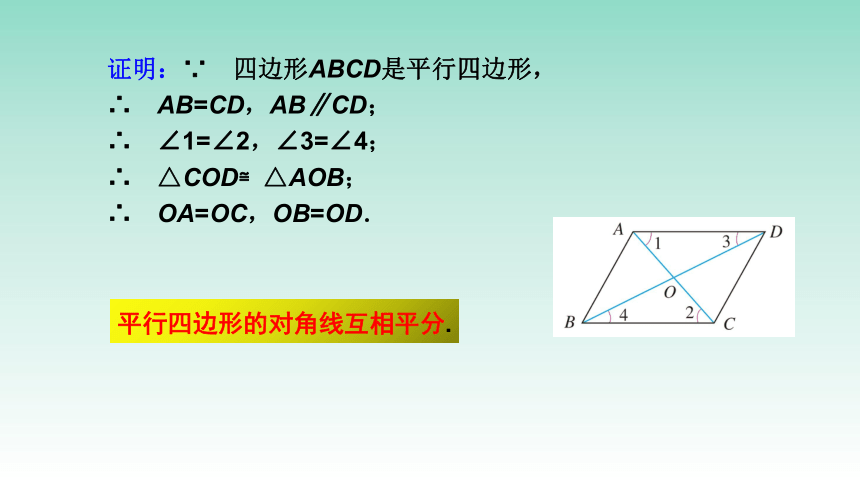
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD;
∴ ∠1=∠2,∠3=∠4;
∴ △COD≌△AOB;
∴ OA=OC,OB=OD.
平行四边形的对角线互相平分.
A
C
D
B
O
平行四边形的对角线互相平分.
平行四边形的性质3
应用格式:
∵四边形ABCD是平行四边形,
∴
OA=OC,OB=OD.
1.平行四边形的两条对角线把它分成的四个三角形(
)
A、都是等腰三角形
B、都是全等三角形
C、都是直角三角形
D、是面积相等的三角形
D
练一练
平行四边形性质3练习
2.口ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC长为(
)
A、5cm
B、15cm
C、6cm
D、16cm
A
3.
平行四边形的两条对角线把它分成的四个三角形(
)
A、都是等腰三角形
B、都是全等三角形
C、都是直角三角形
D、是面积相等的三角形
D
4.判断对错
(1)在口ABCD中,AC交BD于O,则
AO=OB=OC=OD.
(?
)
(2)平行四边形两条对角线的交点到一组对
边的距离相等.
(??
)
(3)平行四边形的两组对边分别平行且相等.
(??
)
(4)平行四边形是轴对称图形.
(
?
)
×
√
√
×
15
5、如图,在
ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是
_________.
O
D
B
A
C
●
1<AD<9
6.
如图,在
ABCD中,BC=10,AC=8,BD=14.
△AOD的周长是多少?△ABC与△DBC的周长哪个长?长多少?
解:∵四边形ABCD是平行四边形
∴AD=BC=10
OA=OC=4
OD=OB=7
∴
l△AOD=
AD+OA+OD=10+4+7=21
∵
AB=CD
BC=BC
BD
–
AC=14
–
8=6
∴△DBC的周长较长,长6.
7、
如图,
ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
A
B
C
D
F
E
O
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD,
OD=OB,
∴OE=OF.
思考
改变直线EF的位置,OE=OF还成立吗?
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
请判断下列图中,OE=OF还成立么?
同2易证明OE=OF还成立.
8
如图,在
ABCD中,AB=10,AD=8,AC⊥BC.
求BC,CD,AC,OA的长,以及
ABCD的面积
解:
∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
∵AC⊥BC.
∴△ABC是直角三角形.
根据勾股定理,
又OA=OC,∴
9
.
在口ABCD中,AC和BD交于点O,AB=4,△AOB的周长为16,求AC+BD的长度.
解∵
l
△AOB=16,AB=4
∴OA+OB=16-4=12
∵四边形ABCD是平行四边形
∴AC=2OA,BD=2OB
∴AC+BD=2OA+2OB
=2(OA+OB)
=2×12=24
1.平行四边形的对边相等;
2.平行四边形的对角相等;
3.平行四边形的对角线互相平分.
(1)本节学行四边形的哪些性质?
(2)结合本节的学习,谈谈研究平行四边形性质的思
想方法.
A
B
C
D
O
注意:研究平行四边形,常常把它转化为三角形问题.
课堂小结
谢谢观看
平行四边形
第2课时
平行四边形的对角线的特征
学习目标
学习重、难点
1.
知道平行四边形的对角线互相平分的性质.
2.能运用这一性质进行推理与计算.
重点:性质的探究.
难点:性质的灵活运用.
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到
晚年的时候,终于拥有了一块平行四边形的土地.由于
年迈体弱,他决定把这块土地平分给他的四个孩子,他
是这样分的:
老大
老二
老三
老四
你觉得他这样分公平吗?说说你的理由.
新课导入
定义:
性质:
两组对边分别平行的四边形叫做
平
行
四边形。
1.平行四边形的两组对边分别平行;
2.平行四边形的对边相等,
3.平行四边形的对角相等,
相邻两角互补。
A
B
C
D
O
复习回顾
A
B
D
C
O
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O
钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
实验操作,提出猜想
●
A
D
O
C
B
D
B
O
C
A
演示
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O
钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
结论:
ABCD绕它的中心O旋转180°后与自身重合,这时我们说
ABCD是中心对称图形点O叫对称中心
有上面的操作演示:
猜想:平行四边形的对角线互相平分.
你能证明上述猜想吗?
猜想:OA=OC,OB=OD
如何证明
如图,在 ABCD中,对角线AC,BD
相交于点O,OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD.
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD;
∴ ∠1=∠2,∠3=∠4;
∴ △COD≌△AOB;
∴ OA=OC,OB=OD.
平行四边形的对角线互相平分.
A
C
D
B
O
平行四边形的对角线互相平分.
平行四边形的性质3
应用格式:
∵四边形ABCD是平行四边形,
∴
OA=OC,OB=OD.
1.平行四边形的两条对角线把它分成的四个三角形(
)
A、都是等腰三角形
B、都是全等三角形
C、都是直角三角形
D、是面积相等的三角形
D
练一练
平行四边形性质3练习
2.口ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC长为(
)
A、5cm
B、15cm
C、6cm
D、16cm
A
3.
平行四边形的两条对角线把它分成的四个三角形(
)
A、都是等腰三角形
B、都是全等三角形
C、都是直角三角形
D、是面积相等的三角形
D
4.判断对错
(1)在口ABCD中,AC交BD于O,则
AO=OB=OC=OD.
(?
)
(2)平行四边形两条对角线的交点到一组对
边的距离相等.
(??
)
(3)平行四边形的两组对边分别平行且相等.
(??
)
(4)平行四边形是轴对称图形.
(
?
)
×
√
√
×
15
5、如图,在
ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是
_________.
O
D
B
A
C
●
1<AD<9
6.
如图,在
ABCD中,BC=10,AC=8,BD=14.
△AOD的周长是多少?△ABC与△DBC的周长哪个长?长多少?
解:∵四边形ABCD是平行四边形
∴AD=BC=10
OA=OC=4
OD=OB=7
∴
l△AOD=
AD+OA+OD=10+4+7=21
∵
AB=CD
BC=BC
BD
–
AC=14
–
8=6
∴△DBC的周长较长,长6.
7、
如图,
ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
A
B
C
D
F
E
O
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD,
OD=OB,
∴OE=OF.
思考
改变直线EF的位置,OE=OF还成立吗?
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
请判断下列图中,OE=OF还成立么?
同2易证明OE=OF还成立.
8
如图,在
ABCD中,AB=10,AD=8,AC⊥BC.
求BC,CD,AC,OA的长,以及
ABCD的面积
解:
∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
∵AC⊥BC.
∴△ABC是直角三角形.
根据勾股定理,
又OA=OC,∴
9
.
在口ABCD中,AC和BD交于点O,AB=4,△AOB的周长为16,求AC+BD的长度.
解∵
l
△AOB=16,AB=4
∴OA+OB=16-4=12
∵四边形ABCD是平行四边形
∴AC=2OA,BD=2OB
∴AC+BD=2OA+2OB
=2(OA+OB)
=2×12=24
1.平行四边形的对边相等;
2.平行四边形的对角相等;
3.平行四边形的对角线互相平分.
(1)本节学行四边形的哪些性质?
(2)结合本节的学习,谈谈研究平行四边形性质的思
想方法.
A
B
C
D
O
注意:研究平行四边形,常常把它转化为三角形问题.
课堂小结
谢谢观看
