2.5.3 切线长定理同步练习(含解析)
文档属性
| 名称 | 2.5.3 切线长定理同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 13:37:01 | ||
图片预览




文档简介
初中数学湘教版九年级下册2.5.3切线长定理 同步练习
一、单选题
1.如图,P为圆O外一点, PA,PB 分别切圆O于 A,B 两点,若 PA=5 ,则 PB= (?? ).
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
2.如图, PA 、 PB 、 AB 与圆O相切, ∠P=60° ,则 ∠AOB= (??? )
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
3.如图,AD , AE分别是⊙O的切线,D , E为切点,BC切⊙O于F , 交AD , AE于点B , C , 若AD=8.则三角形ABC的周长是(????? )
A.?8??????????????????????????????????????B.?10??????????????????????????????????????C.?16??????????????????????????????????????D.?不能确定
4.如图,AB、AC是圆O的两条切线,切点为B、C且∠BAC=50°,D是优弧BDC上一动点(不与B、C重合),则∠BDC的度数为(? )
A.?130°???????????????????????????????B.?65°???????????????????????????????C.?50°或130°???????????????????????????????D.?65°或115°
5.如图, PA 切 ⊙O 于点 A,PB 切 ⊙O 于点 B,PO 交 ⊙O 于点 C ,下列结论中不一定成立的是(? )
A.?PA=PB????????????????B.?PO 平分 ∠APB????????????????C.?AB⊥OP????????????????D.?∠PAB=2∠APO
6.如图PA,PB分别与 ⊙O 相切于A,B两点.若 ∠C=65° ,则 ∠P 的度数为(??? )
A.?65°???????????????????????????????????B.?130°???????????????????????????????????C.?50°???????????????????????????????????D.?115°
7.如图,AB,BC,CD,DA都是⊙O的切线,已知AD=2,BC=5,则AB+CD的值是(?? )
A.?14??????????????????????????????????????????B.?12??????????????????????????????????????????C.?9??????????????????????????????????????????D.?7
8.如图,AB,AC,BD是⊙O的切线,切点分别是P,C,D.若AC=5,BD=3,则AB的长是( )
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?6???????????????????????????????????????????D.?8
9.《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:“今有勾八步,股十五步,问勾中容圆,径几何?”其意思是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径是(?? )
A.?5步??????????????????????????????????????B.?6步??????????????????????????????????????C.?8步??????????????????????????????????????D.?10步
10.如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点 A 为60°角与直尺交点,点 B 为光盘与直尺唯一交点,若 AB =3 ,则光盘的直径是(??? ).
A.?63????????????????????????????????????????B.?33????????????????????????????????????????C.?6????????????????????????????????????????D.?3
二、填空题
11.如图,PA、PB是⊙O的切线,若∠APO=25°,则∠BPA=________.
12.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过弧DE (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为________.
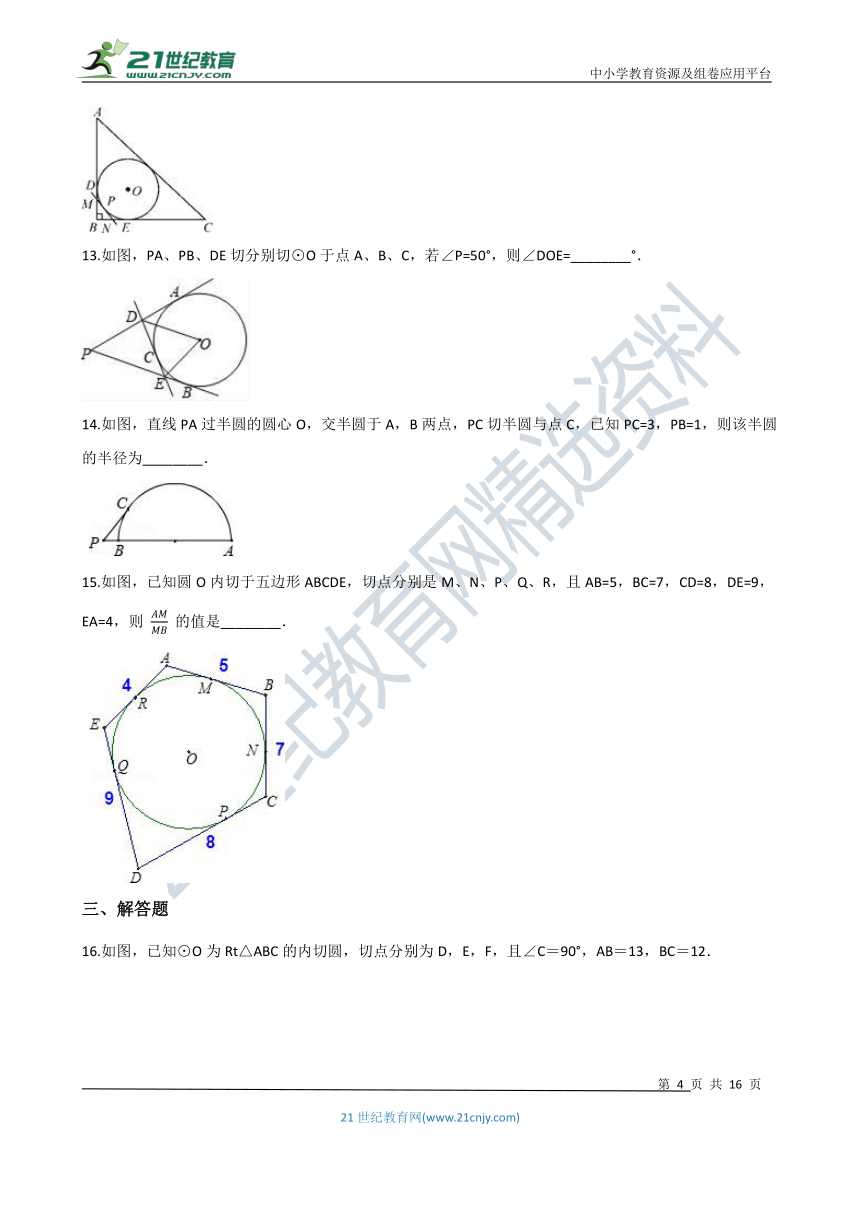
13.如图,PA、PB、DE切分别切⊙O于点A、B、C,若∠P=50°,则∠DOE=________°.
14.如图,直线PA过半圆的圆心O,交半圆于A,B两点,PC切半圆与点C,已知PC=3,PB=1,则该半圆的半径为________.
15.如图,已知圆O内切于五边形ABCDE,切点分别是M、N、P、Q、R,且AB=5,BC=7,CD=8,DE=9,EA=4,则 AMMB 的值是________.
三、解答题
16.如图,已知⊙O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12.
(1)求BF的长;
(2)求⊙O的半径r.
17.如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
(1)求△PDE的周长;
(2)求∠DOE的度数.
18.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
答案解析部分
一、单选题
1. D
考点:切线长定理
解:∵P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=5,
∴PB=PA=5,
故答案为:D.
分析:由切线长定理“从圆外一点引圆的两条切线,它们的切线长相等”可求解.
2. B
考点:切线长定理
解:设PA、PB、AB分别与⊙O相切于点C、D、E,然后连接OC、OD、OE,如图所示:
∵ PA 、 PB 、 AB 与圆O相切,
∴∠OCA=∠ODB=∠OEB=90°,OC=OD=OE,
∴OA、OB分别平分∠EOC、∠EOD,
∵∠P=60°,
∴∠COD=120°,
∴ ∠AOE=12∠COE,∠BOE=12∠EOD ,
∴ ∠AOB=∠AOE+∠BOE=12(∠EOC+∠EOD)=60° ,
故答案为:B.
分析:设PA、PB、AB分别与⊙O相切于点C、D、E,然后连接OC、OD、OE,由题可知:∠AOE=12∠COE,∠BOE=12∠EOD , 再利用四边形的内角和求出∠COD的度数即可。
3. C
考点:切线长定理
解:由切线长定理得: AE=AD=8,BD=BF,CE=CF ,
则三角形ABC的周长为 AB+BC+AC=AB+BF+CF+AC ,
=(AB+BD)+(CE+AC) ,
=AD+AE ,
=8+8 ,
=16 ,
故答案为:C.
分析:先根据切线长定理可得 AE=AD=8,BD=BF,CE=CF ,再根据三角形的周长公式、等量代换即可得.
4. B
考点:切线长定理
解:连接BO,CO,
∵AB、AC是⊙O的两条切线,切点分别为B、C,
∴∠ABO=∠ACO=90°,
∵∠BAC=50°,
∴∠BOC=130°,
∴∠BDC=65°.
故答案为:B.
分析:直接利用切线的性质得到∠ABO=∠ACO=90°,进而利用四边形内角和定理得出∠BOC=100°,再利用圆周角定理得出答案。
5. D
考点:切线长定理
解:连接OA,OB,AB,AB交PO于点G,
由切线长定理可得:∠APO=∠BPO,PA=PB,
又∵PG=PG,
∴△PAG≌△PBG,
从而AB⊥OP.
因此A.B.C都符合题意.
无法得出AB=PA=PB,可知:D是错误的.
综上可知:只有D是错误的.
故答案为:D.
分析:根据切线长定理证出△PAG≌△PBG,再利用全等的性质逐项判定即可。
6. C
考点:切线长定理
解:∵PA、PB是⊙O的切线,
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°,
又∵∠AOB=2∠C=130°,
则∠P=360°-(90°+90°+130°)=50°.
故答案为:C.
分析:根据圆周角的性质求出∠AOB=2∠C=130°,再根据切线的性质得到∠OAP=∠OBP=90°,最后利用四边形的内角和求解即可。
7. D
考点:切线长定理
解:∵AB、BC、CD、DA都是⊙O的切线,
∴可以假设切点分别为E、H、G、F,
∴AF=AE,BE=BH,CH=CG,DG=DF,
∴AD+BC=AF+DF+BH+CH=AE+BE+DG+CG=AB+CD,
∵AD=2,BC=5,
∴AB+CD=AD+BC=7,
故答案为:D.
分析:根据切线长定理,可以证明圆的外切四边形的对边和相等,由此即可解决问题.
8. D
考点:切线长定理
解:∵AB,AC,BD是⊙O的切线,切点分别是P,C,D,
∴AC=AP,BP=BD,
∵AC=5,BD=3
∴AB=AP+BP=AC+BD=5+3=8.
故答案为:D.
分析:利用切线长定理可证得AC=AP,BP=BD,再结合已知条件可求出AB的长。
9. B
考点:切线长定理
解:勾股定理知,斜边是 82+152 =17,利用切线长定理知,
半径= 8+15-172 =3,直径是6.
故答案为:B.
分析:先利用勾股定理求出斜边的长,然后利用公式计算.即直角△ABC的三边长为a,b,c(斜边),则其内切圆的半径r=a+b-c2.
10. A
考点:切线长定理
解:设三角板与圆的切点为C , 连接OA、OB , 如下图所示:
由切线长定理知 AB=AC=3,OA平分∠BAC ,
∴ ∠OAB=60° ,
在 Rt△ABO 中, tan∠OAB=OBAB
∴ OB=ABtan∠OAB=3×3=33
∴光盘的直径为 63 ,
故答案为:A.
分析:设三角板与圆的切点为C , 连接 OA、OB ,由切线长定理得出 AB=AC=3 、 ∠OAB=60° ,根据 tan∠OAB=OBAB 可得答案.
二、填空题
11. 50°
考点:切线长定理
解:∵PA、PB是⊙O的切线,
∴∠BPO=∠APO=25°,
∴∠BPA=50°,
故答案为:50°.
分析:根据切线长定理得到∠BPO=∠APO,结合图形计算,得到答案.
12. 2r
考点:切线长定理
解:连接OD、OE,
求出∠ODB=∠DBE=∠OEB=90°,推出四边形ODBE是正方形,得出BD=BE=OD=OE=r,根据切线长定理由MN与⊙O相切于点P,且⊙O是△ABC的内切圆,得出MP=DM,NP=NE,代入MB+NB+MN=MB+BN+NE+DM=BD+BE=r+r=2r,
故答案为:2r.
分析:连接OD、OE,可得∠ODB=∠DBE=∠OEB=90°,可得推出四边形ODBE是正方形,利用正方形的性质可得BD=BE=OD=OE=r,根据切线长定理可得MP=DM,NP=NE,根据MB+NB+MN=MB+BN+NE+DM=BD+BE,即可求出结论.
13. 65
考点:切线长定理
解:连接OA、OC、OB,
∵OA⊥PA,OB⊥PB,OC⊥DE,
∴∠DAO=∠EBO=90°,
∴∠P+∠AOB=180°,
∴∠AOB=180°﹣50°=130°;
∵∠AOD=∠DOC,∠COE=∠BOE,
∴∠DOE= 12 ∠AOB= 12 ×130°=65°.
故答案为:65.
分析:连接OA、OC、OB,根据切线的性质定理可得∠DAO=∠EBO=90°,由是必须的内角和为360°可得∠P+∠AOB=180°,由此求得∠AOB=130°,由切线长定理可得∠AOD=∠DOC,∠COE=∠BOE,从而得∠DOE= 12 ∠AOB=65°.
14. 4
考点:切线长定理
解:∵PC切半圆与点C,
∴PC2=PA?PB,
即PA=9,
则AB=9﹣1=8,
则圆的半径是4.
故答案为4.
分析:利用切割线定理得出PC2=PA?PB,利用等积式即可算出AB的长,进而得出答案。
15.
考点:切线长定理
解:设AM=x,BM=y,
∵圆O内切于五边形ABCDE,
∴AM=AR,BM=BN,CN=CP,DP=DQ,EQ=ER,AR=AM,
∴BN=y,
∵AB=5,
∴x+y=5,
∵BC=7,
∴CN=CP=7﹣y,
∵CD=8,∴DQ=DP=y+1,
∵DE=9,
∴EQ=ER=8﹣y,
∵EA=4,
∴AR=AM=y﹣4,
∴y﹣4=x,
∴ {x+y=5y-4=x ,
解得: {x=12y=92 ,
∴AM= 12 ,MB= 92 ,
∴ AMMB = 1292 = 19 ;
故答案为: 19
分析:设AM=x,BM=y,根据切线长定理得出AM=AR,BM=BN,CN=CP,DP=DQ,EQ=ER,AR=AM,进而得出x+y=5,①,y﹣4=x,②,解由①②组成的方程组,即可得出x,y的值,从而求出答案。
三、解答题
16. (1)解:在Rt△ABC中,∵∠C=90°,AB=13,BC=12,
∴AC= AB2-BC2 = 132-122 =5,
∵⊙O为Rt△ABC的内切圆,切点分别为D,E,F,
∴BD=BF,AD=AE,CF=CE,
设BF=BD=x,则AD=AE=13﹣x,CFCE=12﹣x,
∵AE+EC=5,
∴13﹣x+12﹣x=5,
∴x=10,
∴BF=10.
(2)解:连接OE,OF,
∵OE⊥AC,OF⊥BC,
∴∠OEC=∠C=∠OFC=90°,
∴四边形OECF是矩形,
∴OE=CF=BC﹣BF=12﹣10=2.
即r=2.
考点:切线长定理
分析:(1)设BF=BD=x,利用切线长定理,构建方程解决问题即可.(2)证明四边形OECF是矩形,推出OE=CF即可解决问题.
17. (1)解:∵PA、PB、DE都为⊙O的切线,
∴DA=DF,EB=EF,PA=PB=6,
∴DE=DA+EB,
∴PE+PD+DE=PA+PB=12,
即△PDE的周长为12
(2)解:连接OF,
∵PA、PB、DE分别切⊙O于A、B、F三点,
∴OB⊥PB,OA⊥PA,∠BOE=∠FOD= ∠BOF,∠FOD=∠AOD= ∠AOF,
∵∠APB=52°,
∴∠AOB=360°﹣90°﹣90°﹣52°=128°,
∴∠DOE=∠FOE+∠FOD= (∠BOF+∠AOF)= ∠BOA=64°.
考点:切线长定理
分析:(1)根据切线长定理得到DA=DF,EB=EF,PA=PB=6,于是得到DE=DA+EB,即可得到结论;(2)根据切线的性质得到OB⊥PB,OA⊥PA,∠BOE=∠FOD= ∠BOF,∠FOD=∠AOD= ∠AOF,根据四边形的内角和得到∠AOB=360°﹣90°﹣90°﹣52°=128°,即可得到结论.
18. (1)解:连接OF;
根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°
(2)解:由(1)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC= =10cm,
∴BE+CG=BC=10cm
(3)解:∵OF⊥BC,
∴OF= =4.8cm
考点:切线长定理
分析:(1)根据切线的性质得到OB平分∠EBF,OC平分∠GCF,OF⊥BC,再根据平行线的性质得∠GCF+∠EBF=180°,则有∠OBC+∠OCB=90°,即∠BOC=90°;(2)由勾股定理可求得BC的长,进而由切线长定理即可得到BE+CG的长;(3)最后由三角形面积公式即可求得OF的长.
一、单选题
1.如图,P为圆O外一点, PA,PB 分别切圆O于 A,B 两点,若 PA=5 ,则 PB= (?? ).
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
2.如图, PA 、 PB 、 AB 与圆O相切, ∠P=60° ,则 ∠AOB= (??? )
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
3.如图,AD , AE分别是⊙O的切线,D , E为切点,BC切⊙O于F , 交AD , AE于点B , C , 若AD=8.则三角形ABC的周长是(????? )
A.?8??????????????????????????????????????B.?10??????????????????????????????????????C.?16??????????????????????????????????????D.?不能确定
4.如图,AB、AC是圆O的两条切线,切点为B、C且∠BAC=50°,D是优弧BDC上一动点(不与B、C重合),则∠BDC的度数为(? )
A.?130°???????????????????????????????B.?65°???????????????????????????????C.?50°或130°???????????????????????????????D.?65°或115°
5.如图, PA 切 ⊙O 于点 A,PB 切 ⊙O 于点 B,PO 交 ⊙O 于点 C ,下列结论中不一定成立的是(? )
A.?PA=PB????????????????B.?PO 平分 ∠APB????????????????C.?AB⊥OP????????????????D.?∠PAB=2∠APO
6.如图PA,PB分别与 ⊙O 相切于A,B两点.若 ∠C=65° ,则 ∠P 的度数为(??? )
A.?65°???????????????????????????????????B.?130°???????????????????????????????????C.?50°???????????????????????????????????D.?115°
7.如图,AB,BC,CD,DA都是⊙O的切线,已知AD=2,BC=5,则AB+CD的值是(?? )
A.?14??????????????????????????????????????????B.?12??????????????????????????????????????????C.?9??????????????????????????????????????????D.?7
8.如图,AB,AC,BD是⊙O的切线,切点分别是P,C,D.若AC=5,BD=3,则AB的长是( )
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?6???????????????????????????????????????????D.?8
9.《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:“今有勾八步,股十五步,问勾中容圆,径几何?”其意思是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径是(?? )
A.?5步??????????????????????????????????????B.?6步??????????????????????????????????????C.?8步??????????????????????????????????????D.?10步
10.如图,是用一把直尺、含60°角的直角三角板和光盘摆放而成,点 A 为60°角与直尺交点,点 B 为光盘与直尺唯一交点,若 AB =3 ,则光盘的直径是(??? ).
A.?63????????????????????????????????????????B.?33????????????????????????????????????????C.?6????????????????????????????????????????D.?3
二、填空题
11.如图,PA、PB是⊙O的切线,若∠APO=25°,则∠BPA=________.
12.如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过弧DE (不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为________.
13.如图,PA、PB、DE切分别切⊙O于点A、B、C,若∠P=50°,则∠DOE=________°.
14.如图,直线PA过半圆的圆心O,交半圆于A,B两点,PC切半圆与点C,已知PC=3,PB=1,则该半圆的半径为________.
15.如图,已知圆O内切于五边形ABCDE,切点分别是M、N、P、Q、R,且AB=5,BC=7,CD=8,DE=9,EA=4,则 AMMB 的值是________.
三、解答题
16.如图,已知⊙O为Rt△ABC的内切圆,切点分别为D,E,F,且∠C=90°,AB=13,BC=12.
(1)求BF的长;
(2)求⊙O的半径r.
17.如图,∠APB=52°,PA、PB、DE都为⊙O的切线,切点分别为A、B、F,且PA=6.
(1)求△PDE的周长;
(2)求∠DOE的度数.
18.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
答案解析部分
一、单选题
1. D
考点:切线长定理
解:∵P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=5,
∴PB=PA=5,
故答案为:D.
分析:由切线长定理“从圆外一点引圆的两条切线,它们的切线长相等”可求解.
2. B
考点:切线长定理
解:设PA、PB、AB分别与⊙O相切于点C、D、E,然后连接OC、OD、OE,如图所示:
∵ PA 、 PB 、 AB 与圆O相切,
∴∠OCA=∠ODB=∠OEB=90°,OC=OD=OE,
∴OA、OB分别平分∠EOC、∠EOD,
∵∠P=60°,
∴∠COD=120°,
∴ ∠AOE=12∠COE,∠BOE=12∠EOD ,
∴ ∠AOB=∠AOE+∠BOE=12(∠EOC+∠EOD)=60° ,
故答案为:B.
分析:设PA、PB、AB分别与⊙O相切于点C、D、E,然后连接OC、OD、OE,由题可知:∠AOE=12∠COE,∠BOE=12∠EOD , 再利用四边形的内角和求出∠COD的度数即可。
3. C
考点:切线长定理
解:由切线长定理得: AE=AD=8,BD=BF,CE=CF ,
则三角形ABC的周长为 AB+BC+AC=AB+BF+CF+AC ,
=(AB+BD)+(CE+AC) ,
=AD+AE ,
=8+8 ,
=16 ,
故答案为:C.
分析:先根据切线长定理可得 AE=AD=8,BD=BF,CE=CF ,再根据三角形的周长公式、等量代换即可得.
4. B
考点:切线长定理
解:连接BO,CO,
∵AB、AC是⊙O的两条切线,切点分别为B、C,
∴∠ABO=∠ACO=90°,
∵∠BAC=50°,
∴∠BOC=130°,
∴∠BDC=65°.
故答案为:B.
分析:直接利用切线的性质得到∠ABO=∠ACO=90°,进而利用四边形内角和定理得出∠BOC=100°,再利用圆周角定理得出答案。
5. D
考点:切线长定理
解:连接OA,OB,AB,AB交PO于点G,
由切线长定理可得:∠APO=∠BPO,PA=PB,
又∵PG=PG,
∴△PAG≌△PBG,
从而AB⊥OP.
因此A.B.C都符合题意.
无法得出AB=PA=PB,可知:D是错误的.
综上可知:只有D是错误的.
故答案为:D.
分析:根据切线长定理证出△PAG≌△PBG,再利用全等的性质逐项判定即可。
6. C
考点:切线长定理
解:∵PA、PB是⊙O的切线,
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°,
又∵∠AOB=2∠C=130°,
则∠P=360°-(90°+90°+130°)=50°.
故答案为:C.
分析:根据圆周角的性质求出∠AOB=2∠C=130°,再根据切线的性质得到∠OAP=∠OBP=90°,最后利用四边形的内角和求解即可。
7. D
考点:切线长定理
解:∵AB、BC、CD、DA都是⊙O的切线,
∴可以假设切点分别为E、H、G、F,
∴AF=AE,BE=BH,CH=CG,DG=DF,
∴AD+BC=AF+DF+BH+CH=AE+BE+DG+CG=AB+CD,
∵AD=2,BC=5,
∴AB+CD=AD+BC=7,
故答案为:D.
分析:根据切线长定理,可以证明圆的外切四边形的对边和相等,由此即可解决问题.
8. D
考点:切线长定理
解:∵AB,AC,BD是⊙O的切线,切点分别是P,C,D,
∴AC=AP,BP=BD,
∵AC=5,BD=3
∴AB=AP+BP=AC+BD=5+3=8.
故答案为:D.
分析:利用切线长定理可证得AC=AP,BP=BD,再结合已知条件可求出AB的长。
9. B
考点:切线长定理
解:勾股定理知,斜边是 82+152 =17,利用切线长定理知,
半径= 8+15-172 =3,直径是6.
故答案为:B.
分析:先利用勾股定理求出斜边的长,然后利用公式计算.即直角△ABC的三边长为a,b,c(斜边),则其内切圆的半径r=a+b-c2.
10. A
考点:切线长定理
解:设三角板与圆的切点为C , 连接OA、OB , 如下图所示:
由切线长定理知 AB=AC=3,OA平分∠BAC ,
∴ ∠OAB=60° ,
在 Rt△ABO 中, tan∠OAB=OBAB
∴ OB=ABtan∠OAB=3×3=33
∴光盘的直径为 63 ,
故答案为:A.
分析:设三角板与圆的切点为C , 连接 OA、OB ,由切线长定理得出 AB=AC=3 、 ∠OAB=60° ,根据 tan∠OAB=OBAB 可得答案.
二、填空题
11. 50°
考点:切线长定理
解:∵PA、PB是⊙O的切线,
∴∠BPO=∠APO=25°,
∴∠BPA=50°,
故答案为:50°.
分析:根据切线长定理得到∠BPO=∠APO,结合图形计算,得到答案.
12. 2r
考点:切线长定理
解:连接OD、OE,
求出∠ODB=∠DBE=∠OEB=90°,推出四边形ODBE是正方形,得出BD=BE=OD=OE=r,根据切线长定理由MN与⊙O相切于点P,且⊙O是△ABC的内切圆,得出MP=DM,NP=NE,代入MB+NB+MN=MB+BN+NE+DM=BD+BE=r+r=2r,
故答案为:2r.
分析:连接OD、OE,可得∠ODB=∠DBE=∠OEB=90°,可得推出四边形ODBE是正方形,利用正方形的性质可得BD=BE=OD=OE=r,根据切线长定理可得MP=DM,NP=NE,根据MB+NB+MN=MB+BN+NE+DM=BD+BE,即可求出结论.
13. 65
考点:切线长定理
解:连接OA、OC、OB,
∵OA⊥PA,OB⊥PB,OC⊥DE,
∴∠DAO=∠EBO=90°,
∴∠P+∠AOB=180°,
∴∠AOB=180°﹣50°=130°;
∵∠AOD=∠DOC,∠COE=∠BOE,
∴∠DOE= 12 ∠AOB= 12 ×130°=65°.
故答案为:65.
分析:连接OA、OC、OB,根据切线的性质定理可得∠DAO=∠EBO=90°,由是必须的内角和为360°可得∠P+∠AOB=180°,由此求得∠AOB=130°,由切线长定理可得∠AOD=∠DOC,∠COE=∠BOE,从而得∠DOE= 12 ∠AOB=65°.
14. 4
考点:切线长定理
解:∵PC切半圆与点C,
∴PC2=PA?PB,
即PA=9,
则AB=9﹣1=8,
则圆的半径是4.
故答案为4.
分析:利用切割线定理得出PC2=PA?PB,利用等积式即可算出AB的长,进而得出答案。
15.
考点:切线长定理
解:设AM=x,BM=y,
∵圆O内切于五边形ABCDE,
∴AM=AR,BM=BN,CN=CP,DP=DQ,EQ=ER,AR=AM,
∴BN=y,
∵AB=5,
∴x+y=5,
∵BC=7,
∴CN=CP=7﹣y,
∵CD=8,∴DQ=DP=y+1,
∵DE=9,
∴EQ=ER=8﹣y,
∵EA=4,
∴AR=AM=y﹣4,
∴y﹣4=x,
∴ {x+y=5y-4=x ,
解得: {x=12y=92 ,
∴AM= 12 ,MB= 92 ,
∴ AMMB = 1292 = 19 ;
故答案为: 19
分析:设AM=x,BM=y,根据切线长定理得出AM=AR,BM=BN,CN=CP,DP=DQ,EQ=ER,AR=AM,进而得出x+y=5,①,y﹣4=x,②,解由①②组成的方程组,即可得出x,y的值,从而求出答案。
三、解答题
16. (1)解:在Rt△ABC中,∵∠C=90°,AB=13,BC=12,
∴AC= AB2-BC2 = 132-122 =5,
∵⊙O为Rt△ABC的内切圆,切点分别为D,E,F,
∴BD=BF,AD=AE,CF=CE,
设BF=BD=x,则AD=AE=13﹣x,CFCE=12﹣x,
∵AE+EC=5,
∴13﹣x+12﹣x=5,
∴x=10,
∴BF=10.
(2)解:连接OE,OF,
∵OE⊥AC,OF⊥BC,
∴∠OEC=∠C=∠OFC=90°,
∴四边形OECF是矩形,
∴OE=CF=BC﹣BF=12﹣10=2.
即r=2.
考点:切线长定理
分析:(1)设BF=BD=x,利用切线长定理,构建方程解决问题即可.(2)证明四边形OECF是矩形,推出OE=CF即可解决问题.
17. (1)解:∵PA、PB、DE都为⊙O的切线,
∴DA=DF,EB=EF,PA=PB=6,
∴DE=DA+EB,
∴PE+PD+DE=PA+PB=12,
即△PDE的周长为12
(2)解:连接OF,
∵PA、PB、DE分别切⊙O于A、B、F三点,
∴OB⊥PB,OA⊥PA,∠BOE=∠FOD= ∠BOF,∠FOD=∠AOD= ∠AOF,
∵∠APB=52°,
∴∠AOB=360°﹣90°﹣90°﹣52°=128°,
∴∠DOE=∠FOE+∠FOD= (∠BOF+∠AOF)= ∠BOA=64°.
考点:切线长定理
分析:(1)根据切线长定理得到DA=DF,EB=EF,PA=PB=6,于是得到DE=DA+EB,即可得到结论;(2)根据切线的性质得到OB⊥PB,OA⊥PA,∠BOE=∠FOD= ∠BOF,∠FOD=∠AOD= ∠AOF,根据四边形的内角和得到∠AOB=360°﹣90°﹣90°﹣52°=128°,即可得到结论.
18. (1)解:连接OF;
根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBE+∠OCF=90°,
∴∠BOC=90°
(2)解:由(1)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC= =10cm,
∴BE+CG=BC=10cm
(3)解:∵OF⊥BC,
∴OF= =4.8cm
考点:切线长定理
分析:(1)根据切线的性质得到OB平分∠EBF,OC平分∠GCF,OF⊥BC,再根据平行线的性质得∠GCF+∠EBF=180°,则有∠OBC+∠OCB=90°,即∠BOC=90°;(2)由勾股定理可求得BC的长,进而由切线长定理即可得到BE+CG的长;(3)最后由三角形面积公式即可求得OF的长.
