2.7 正多边形与圆同步练习(含解析)
图片预览


文档简介
初中数学湘教版九年级下册2.7正多边形与圆 同步练习
一、单选题
1.下列几何图形中,既是中心对称图形又是轴对称图形的个数是(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.在半径为R的圆上依次截取等于R的弦,顺次连接各分点得到的多边形是( )
A.?正三角形???????????????????????????B.?正四边形???????????????????????????C.?正五边形???????????????????????????D.?正六边形
3.已知一个正多边形的每个内角是 150? ,则这个正多边形是(?? )
A.?正八边形?????????????????????????B.?正十边形?????????????????????????C.?正十二边形?????????????????????????D.?正十四边形
4.如图,正六边形ABCDEF内接于于⊙O,连接BD,则∠CBD的度数是(?? )
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?60°???????????????????????????????????????D.?90°
5.下列说法正确的是(?? )
A.?五条长度相等的线段首尾顺次相接所构成的图形是正五边形
B.?正六边形各内角都相等,所以各内角都相等的六边形是正六边形
C.?从n边形的一个顶点出发可以引(n-2)条对角线
D.?n边形共有 n(n-3)2 条对角线
6.若一个正多边形的一个内角为 144? ,则这个图形为正(?? )边形.
A.?八?????????????????????????????????????????B.?九?????????????????????????????????????????C.?七?????????????????????????????????????????D.?十
7.正六边形的边长为 2a ,则它的面积为(?? )
A.?3a2?????????????????????????????????B.?323a2?????????????????????????????????C.?33a2?????????????????????????????????D.?63a2
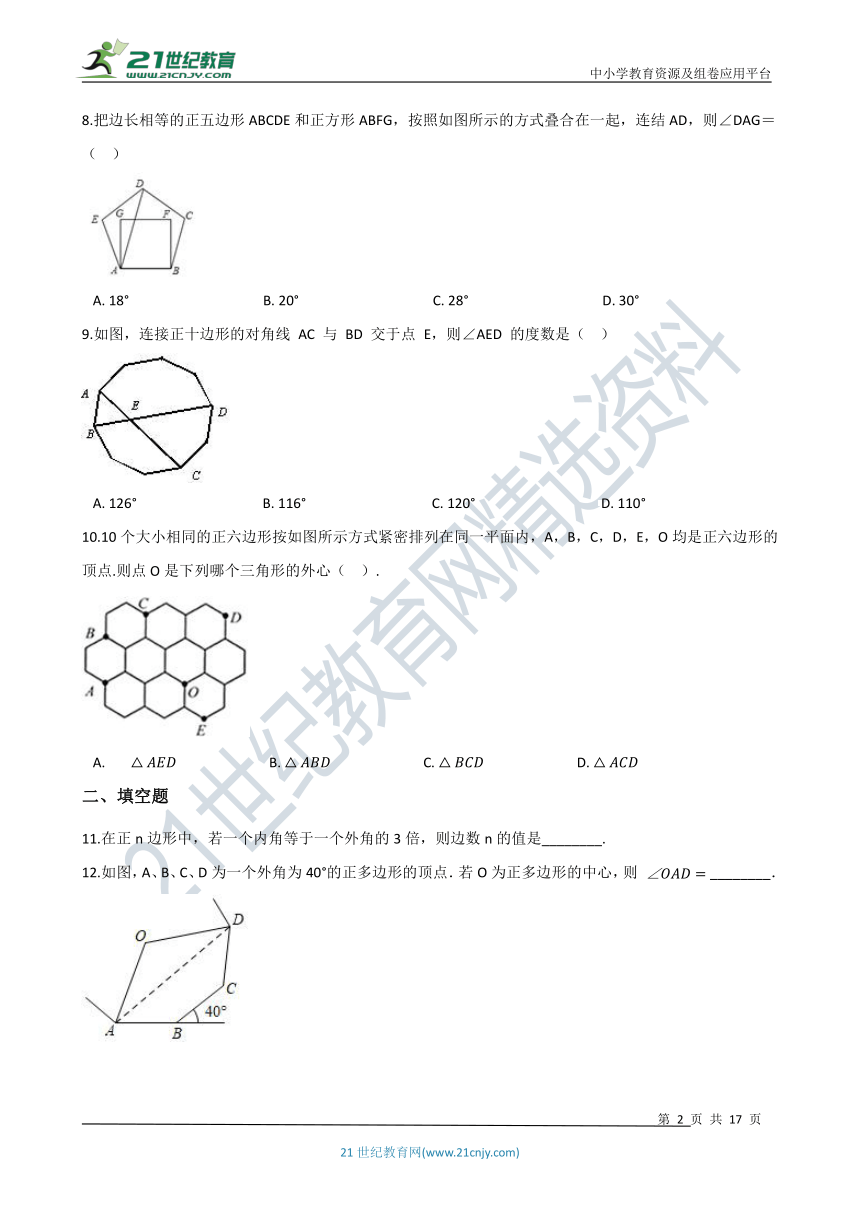
8.把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=(?? )
A.?18°???????????????????????????????????????B.?20°???????????????????????????????????????C.?28°???????????????????????????????????????D.?30°
9.如图,连接正十边形的对角线 AC 与 BD 交于点 E,则∠AED 的度数是(?? )
A.?126°????????????????????????????????????B.?116°????????????????????????????????????C.?120°????????????????????????????????????D.?110°
10.10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A,B,C,D,E,O均是正六边形的顶点.则点O是下列哪个三角形的外心(?? ).
A.??? △AED???????????????????????????B.?△ABD???????????????????????????C.?△BCD???????????????????????????D.?△ACD
二、填空题
11.在正n边形中,若一个内角等于一个外角的3倍,则边数n的值是________.
12.如图,A、B、C、D为一个外角为40°的正多边形的顶点.若O为正多边形的中心,则 ∠OAD= ________.
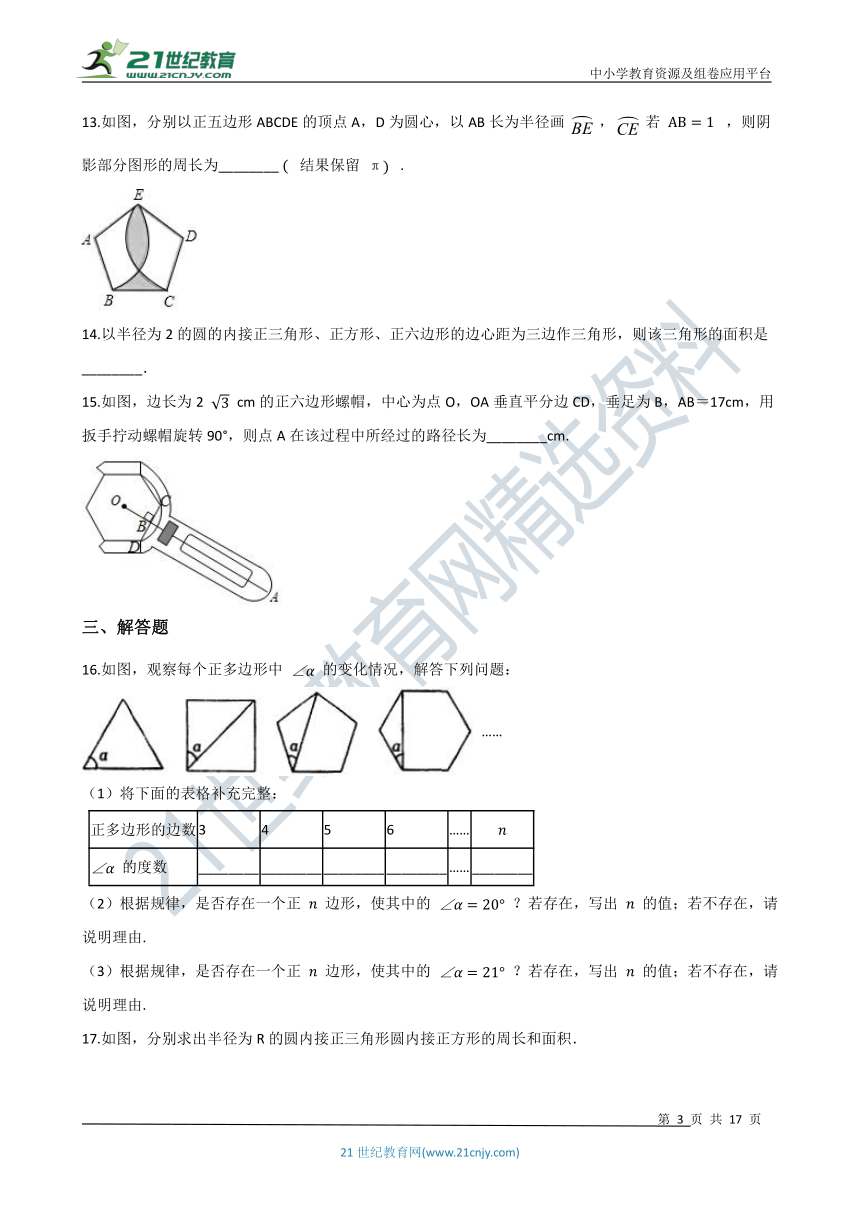
13.如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画??,?若 AB=1 ?,则阴影部分图形的周长为________ ( ?结果保留 π) ?.
14.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是________.
15.如图,边长为2 3 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为________cm.
三、解答题
16.如图,观察每个正多边形中 ∠α 的变化情况,解答下列问题:
……
(1)将下面的表格补充完整:
正多边形的边数
3
4
5
6
……
n
∠α 的度数
________
________
________
________
……
________
(2)根据规律,是否存在一个正 n 边形,使其中的 ∠α=20° ?若存在,写出 n 的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正 n 边形,使其中的 ∠α=21° ?若存在,写出 n 的值;若不存在,请说明理由.
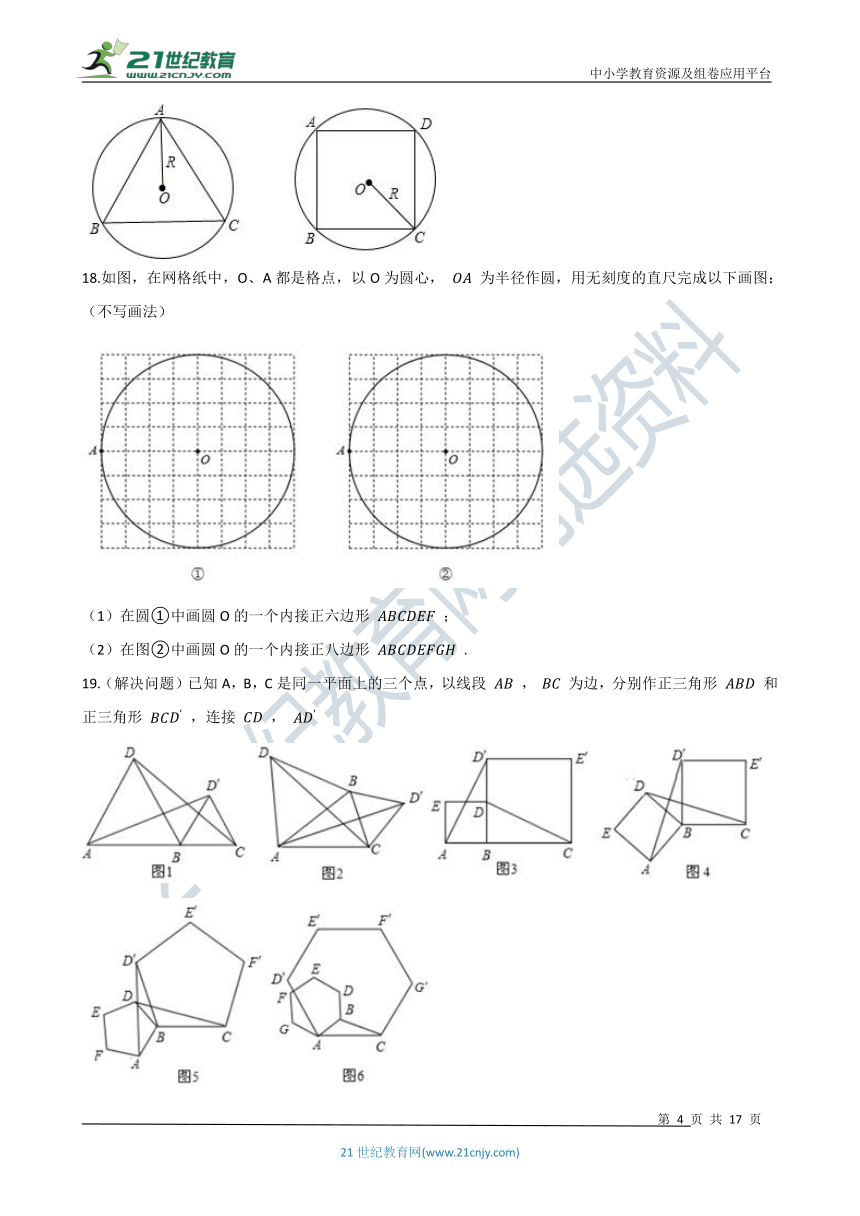
17.如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
18.如图,在网格纸中,O、A都是格点,以O为圆心, OA 为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
(1)在圆①中画圆O的一个内接正六边形 ABCDEF ;
(2)在图②中画圆O的一个内接正八边形 ABCDEFGH .
19.(解决问题)已知A,B,C是同一平面上的三个点,以线段 AB , BC 为边,分别作正三角形 ABD 和正三角形 BCD' ,连接 CD , AD'
(1)如图1,当点A,B,C在同一直线上时,线段 CD 与 AD' 的大小关系是________;
(2)如图2,当A,B,C为三角形的顶点时(点A,B, D' 不在同一条直线上),判断线段 CD 与 AD' 的大小关系是否发生改变,并说明理由;
(3)(类比猜想)
已知A,B,C是同一平面上的三个点,以线段 AB , BC 为边,分别作正方形,连接 CD , AD' ,如图3和图4所示.判断线段 CD 与 AD' 的大小关系,并在图4(点A,B, D' 不在同一条直线上)中证明你的判断;
?
(4)(推广应用)
上面的这些结论能否推广到任意正多边形(不必证明)?
(5)如图5, CD 与 AD' 的大小关系是________,并写出它们分别在哪两个全等三角形中________;
(6)请在图6中连接图中两个顶点,构造处一组全等三角形,并写出这两个全等的三角形.
答案解析部分
一、单选题
1. B
考点:轴对称图形,中心对称及中心对称图形
解:第二个图形、第四个图形既是中心对称图形又是轴对称图形,共2个.
故答案为:B.
分析:根据中心对称图形以及轴对称图形的含义,判断得到答案即可。
2. D
考点:正多边形的性质
解:由题意这个正n边形的中心角=60°,
∴n= 360°60° =6
∴这个多边形是正六边形,
故答案为:D.
分析:求出正多边形的中心角即可解决问题.
3. C
考点:多边形内角与外角,正多边形的性质
解:∵一个正多边形的每个内角为150°,
∴这个正多边形的每个外角=180°-150°=30°,
∴这个正多边形的边数= 360°30° ?=12.
故答案为:C.
分析:根据多边形的一个内角和它相邻的外角互补可求得一个外角的度数,再根据多边形的外角和等于360°和正多边形的各个外角都相等可求解.
4. A
考点:圆内接正多边形
解:∵ 正六边形ABCDEF ,
∴∠BCD=180°-(360°÷6)=120°,
∵CB=CD,
∴∠CBD=180°-120°2=30°;
故答案为:A.
分析:先根据正多边形的外角和求出这个正六边形的一个内角的度数,再结合等腰三角形的性质,利用三角形的内角和定理即可求出∠CBD的度数.
5. D
考点:多边形的对角线,正多边形的性质
解:A、五条长度相等的线段首尾顺次相接所构成的图形不一定是正五边形,故本选项说法错误,不符合题意;
B、正六边形各内角都相等,但各内角都相等的六边形不一定是正六边形,故本选项说法错误,不符合题意;
C、从n边形的一个顶点出发可以引(n-3)条对角线,本选项说法错误,不符合题意;
D、n边形共有 n(n-3)2 条对角线,故本选项说法正确,符合题意.
故答案为:D.
分析:根据正多边形的定义即可判断A、B两项,根据多边形对角线的性质和条数公式即可判断C、D两项,进而可得答案.
6. D
考点:多边形内角与外角,正多边形的性质
解:设所求正n边形边数为n,?则 144°?n=(n-2)?180° ,
解得 n=10 ,
故答案为:D.
分析:利用多边形的内角和定理建立方程计算得结论.
7. D
考点:解直角三角形,正多边形的性质
解:设O是正六边形的中心,AB是正六边形的一边,OC是边心距
∵ ∠AOB=360°6=60°,OA=OB
∴△OAB是正三角形.
∴AO=AB=2a,∠OAB=60° ?
∵OC=OA?sin∠OAB= 2a·32=3a ,
∴S△OAB= 12 AB?OC= 12×2a×3a=3a2 ,
∴正六边形的面积为 6×3a2=63a2 .
故答案为::D.
分析:由题意画出图形,设O是正六边形的中心,AB是正六边形的一边,OC是边心距,由正多边形的性质可得△OAB是正三角形,解直角三角形OAC可求得OC的长,然后根据S正六边形=6×S△AOB可求解.
8. A
考点:等腰三角形的性质,正多边形的性质
解:∵正五边形ABCDE和正方形ABFG
∴∠EAB=∠E=5-2×180°5=108° , ∠GAB=90°,EA=ED,
∴∠EAD=12180°-108°=36°
∴∠BAD=∠EAB-∠EAD=108°-36°=72°,
∴∠GAD=∠GAB-∠BAD=90°-72°=18°.
故答案为:A.
分析:正多边形的内角和定理求出∠EAB,EA=ED,∠GAB的度数,再利用等腰三角形的性质及三角形内角和定理,可求出∠EAD,∠BAD的度数;然后根据∠GAD=∠GAB-∠BAD,可求出∠GAD的度数。
9. A
考点:三角形的外角性质,正多边形的性质
解:正十边形的每个内角的度数为 (10-2)×180°10=144° ,
则 ∠BAE=12×[(5-2)×180°-144°×3]=54° ,
∠ABE=12×[(6-2)×180°-144°×4]=72° ,
由三角形的外角性质得: ∠AED=∠BAE+∠ABE=126° ,
故答案为:A.
分析:根据正十边形的性质求出各内角的度数,再根据正五边形及正六边形的内角和公式分别求出∠BAE、∠ABE的度数,最后利用三角形外角的性质进行解答即可.
10. D
考点:三角形的外接圆与外心,正多边形的性质
解:因为三角形的外心到三角形的三个顶点的距离相等,所以由正六边形性质可知,点O到A,B,C,D,E的距离中,只有OA=OC=OD.
故答案为:D.
分析:根据三角形外心的性质,到三个顶点的距离相等,可以依次判断.
二、填空题
11. 8
考点:多边形内角与外角,正多边形的性质
解:设多边形的外角是x,则内角是3x.
则 x+3x=180° ,
解得 x=45° .
∴n=36045=8 .
故答案为8.
分析:本题考查了正多边形的外角与内角的知识,设外角为x,则其内角为3x , 然后利用正多边形的内角与外角互补列出方程求得x的值,然后根据多边形的外角和为 360° 求边数即可.
12. 30°
考点:三角形内角和定理,等腰三角形的性质,正多边形的性质
解:多边形的每个外角相等,且其和为 360?
据此可得多边形的边数为: 36040=9
∴ ∠AOD=3×360?9=120?
∵OA=OD
∴ ∠OAD=∠ODA=180?-∠AOD2=180?-120?2=30?
故答案为:30°.
分析:利用正多边形的边数=360°÷一个外角的度数,可求出此多边形的边数,再求出∠AOD的度数,再利用等边对等角及三角形的内角和定理求出∠OAD的度数。
13. 65π +1
考点:弧长的计算,正多边形的性质
解:∵五边形ABCDE为正五边形,AB=1,∴AB=BC=CD=DE=EA=1,∠A=∠D=108°,∴ BE? = CE? = 108180 ?πAB= 35π ,∴C阴影=?BE? +?CE? +BC= 65π +1.
故答案为: 65π +1.
分析:观察图形可知,阴影部分的周长=弧BE+弧CE+BC,根据弧长公式l=nπR180可求解.
14. 22
考点:圆内接正多边形
解:如图所示,
∵OC=2,
∴OD=2×sin30°=1;
如图所示,
∵OC=2,
∴OD=2×sin45°= 2 ;
如图所示,
∵OA=2,
∴OD=2×cos30°= 3 ,
则该三角形的三边分别为:, 2 , 3 ,
∵12+( 2 )2=( 3 )2 ,
∴该三角形是直角边,
∴该三角形的面积是: 12 ×1× 2 = 22 .
故答案为 22 .
分析:由于内接正三角形、正方形、正六边形是特殊内角的多边形,可构造直角三角形分别求出边心距的长,再由勾股定理逆定理可得该三角形是直角三角形,进而可得其面积.
15. 10π
考点:圆内接正多边形,弧长的计算
解:连接OD,OC.
∵∠DOC=60°,OD=OC,
∴△ODC是等边三角形,
∴OD=OC=DC= 23 (cm),
∵OB⊥CD,
∴BC=BD= 3 (cm),
∴OB= 3 BC=3(cm),
∵AB=17cm,
∴OA=OB+AB=20(cm),
∴点A在该过程中所经过的路径长= 90?π?20180 =10π(cm),
故答案为:10π.
分析:利用正六边形的性质求出OB的长度,进而得到OA的长度,根据弧长公式进行计算即可.
三、解答题
16. (1)60°;45°;36°;30°;180°n
(2)存在一个正 n 边形,使其中的 ∠α=20°
理由是:根据题意得: (180n)°=20° ,解得: n=9 ,
即当多边形是正九边形,能使其中的 ∠α=20° ;
(3)不存在,理由如下:
假设存在正 n 边形使得 ∠α=21° ,得 ∠α=21°=(180n)° ,
解得: n=847 ,与 n 是正整数矛盾,
所以不存在正 n 边形使得 ∠α=21° .
考点:多边形内角与外角,圆内接正多边形
解:(1)填表如下:
正多边形的边数
3
4
5
6
……
n
∠α 的度数
60°
45°
36°
30°
……
(180n)°
60° , 45° , 36° , 30° , 180°n ;(可以观察归纳出来,也可以计算出来).
分析:(1)首先根据多边形的内角公式:(n-2)×180°,将n=3、4、5、6、8、12代入公式分别计算出各多边形的内角和;然后再根据多边形的外角和为360°,即可得到各多边形的内角和,进而完成表格.(2)依据题意得∠α=20°= 180°n ,即可求出n的值。(3)依据题意∠α=21°= 180°n ,求出n的值是否为正整数即可.
17. 解:如图1,连接OB、OC,过O作OD⊥AB于D,
∵⊙O是正三角形ABC的外接圆,
∴∠AOB= 360°3 =120°,
∵OA=OB,
∴∠AOD=∠BOD=60°,
在Rt△ADO中,AO=R,AD=R×sin60°= 32 R,OD=Rcos60°= 12 R,
∵OD⊥AB,
∴AB=2AD= 3 R,
∴正△ABC的周长是3AB=3 3 R;面积是3× 12 AB×OD=3× 12 × 3 R× 12 R= 34 R2;
如图2,连接OA、OB、OD,
∵⊙O是正方形ABCD的外接圆,
∴∠COD= 360°4 =90°,
∵OD=OC=R,由勾股定理得;CD= R2+R2 = 2 R,
∴正方形ABCD的周长为4× 2 R=4 2 R,面积为 2 R× 2 R=2R2 .
考点:圆内接正多边形,解直角三角形
分析: 如图1,连接OB、OC,过O作OD⊥AB于D, 利用正多边形和圆的性质,可得出∠AOD=60°,由OA=R,利用解直角三角形分别求出AD、OD,即可求出AB的长,继而可求出△ABC的周长,再由△ABC的面积=3×△AOB的面积,即可求解;如图2, 连接OA、OB、OD,利用正方形的性质,可知∠COD=90°,OC=OD=R,利用勾股定理求出CD,然后求出正方形ABCD的周长和面积。
?18. (1)解:设AO的延长线与圆交于点D,
根据圆的内接正六边形的性质,点D即为正六边形的一个顶点,且正六边形的边长等于圆的半径,即OB=AB,故在图中找到AO的中垂线与圆的交点即为正六边形的顶点B和F;同理:在图中找到OD的中垂线与圆的交点即为正六边形的顶点C和E,连接AB、BC、CD、DE、EF、FA,如图①,正六边形 ABCDEF 即为所求.
(2)解:圆的内接八边形的中心角为360°÷8=45°,而正方形的对角线与边的夹角也为45°
∴在如②图所示的正方形OMNP中,连接对角线ON并延长,交圆于点B,此时∠AON=45°;∵∠NOP=45°,
∴OP的延长线与圆的交点即为点C
同理,即可确定点D、E、F、G、H的位置,顺次连接,
如图②,正八边形 ABCDEFGH 即为所求.
考点:正方形的性质,圆内接正多边形,正多边形的性质
分析:(1)设AO的延长线与圆交于点D,根据正六边形的性质,点D即为正六边形的一个顶点,且正六边形的边长等于圆的半径,根据垂直平分线的性质即可确定其它的顶点;(2)先求出内接八边形的中心角,然后根据正方形的性质即可找到各个顶点.
19. (1)解:相等
(2)解:线段 CD 与 AD' 的大小关系没有改变,理由如下:
∵△ABD、△BCD’是等边三角形,
∴AB=BD,BD’=BC, ∠ABD=∠CBD'=60°
∵ ∠ABD'=∠ABC+∠CBD' , ∠DBC=∠ABC+∠ABD
∴ ∠ABD'=∠DBC
∴△ABD’≌△DBC(SAS)
∴ CD = AD'
(3)解:在如图3和图4.判断线段 CD 与 AD' 的大小关系为相等,理由如下:
∵四边形ABDE、四边形BCD’E’是正方形,
∴AB=BD,BD’=BC, ∠ABD=∠CBD'=90°
∵ ∠ABD'=∠ABD+∠DBD' , ∠DBC=∠D'BC+∠DBD'
∴ ∠ABD'=∠DBC
∴△ABD’≌△DBC(SAS)
∴ CD = AD'
故线段 CD 与 AD' 的大小关系为相等;
(4)能推广到任意正多边形
(5)相等;△ABD’≌△DBC
(6)解:如图,连接GD’,
∵六边形ABDEFG、六边形ACG’F’E’ D’是正方形,
∴AB=AG,AD’=AC, ∠GAB=∠CAD'=120°
∵ ∠GAD'=∠GAB-∠BAD' , ∠BAC=∠D'AC-∠BAD'
∴ ∠GAD'=∠BAC
∴△GAD’≌△BAC(SAS)
故答案为△GAD’≌△BAC.
考点:三角形全等及其性质,正多边形的性质
解:(1)∵△ABD、△BCD’是等边三角形,
∴AB=BD,BD’=BC, ∠ABD=∠CBD'=60°
∵ ∠ABD'=∠ABD+∠DBD' , ∠DBC=∠D'BC+∠DBD'
∴ ∠ABD'=∠DBC
∴△ABD’≌△DBC(SAS)
∴ CD = AD'
故答案为:相等;(4)根据题意及图形的特点同理可得△ABD’≌△DBC,则 CD = AD'
故线段 CD 与 AD' 的大小关系为相等,能推广到任意正多边形;(5)∵五边形ABDEF、五边形BCF’E’ D’是正方形,
∴AB=BD,BD’=BC, ∠ABD=∠CBD'=108°
∵ ∠ABD'=∠ABD+∠DBD' , ∠DBC=∠D'BC+∠DBD'
∴ ∠ABD'=∠DBC
∴△ABD’≌△DBC(SAS)
∴ CD = AD'
故答案为:相等;△ABD’≌△DBC;
分析:(1)根据正三角形的性质证明△ABD’≌△DBC,即可求解;(2)同理证明△ABD’≌△DBC,即可求解;(3)根据正方形的性质同理证明△ABD’≌△DBC,即可求解;(4)根据题意及图形的特点可知这些结论能否推广到任意正多边形;(5)根据正五边形的性质同理证明△ABD’≌△DBC,即可求解;(6)连接GD’,证明△ABC≌△AGD’即可求解.
、
一、单选题
1.下列几何图形中,既是中心对称图形又是轴对称图形的个数是(?? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.在半径为R的圆上依次截取等于R的弦,顺次连接各分点得到的多边形是( )
A.?正三角形???????????????????????????B.?正四边形???????????????????????????C.?正五边形???????????????????????????D.?正六边形
3.已知一个正多边形的每个内角是 150? ,则这个正多边形是(?? )
A.?正八边形?????????????????????????B.?正十边形?????????????????????????C.?正十二边形?????????????????????????D.?正十四边形
4.如图,正六边形ABCDEF内接于于⊙O,连接BD,则∠CBD的度数是(?? )
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?60°???????????????????????????????????????D.?90°
5.下列说法正确的是(?? )
A.?五条长度相等的线段首尾顺次相接所构成的图形是正五边形
B.?正六边形各内角都相等,所以各内角都相等的六边形是正六边形
C.?从n边形的一个顶点出发可以引(n-2)条对角线
D.?n边形共有 n(n-3)2 条对角线
6.若一个正多边形的一个内角为 144? ,则这个图形为正(?? )边形.
A.?八?????????????????????????????????????????B.?九?????????????????????????????????????????C.?七?????????????????????????????????????????D.?十
7.正六边形的边长为 2a ,则它的面积为(?? )
A.?3a2?????????????????????????????????B.?323a2?????????????????????????????????C.?33a2?????????????????????????????????D.?63a2
8.把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=(?? )
A.?18°???????????????????????????????????????B.?20°???????????????????????????????????????C.?28°???????????????????????????????????????D.?30°
9.如图,连接正十边形的对角线 AC 与 BD 交于点 E,则∠AED 的度数是(?? )
A.?126°????????????????????????????????????B.?116°????????????????????????????????????C.?120°????????????????????????????????????D.?110°
10.10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A,B,C,D,E,O均是正六边形的顶点.则点O是下列哪个三角形的外心(?? ).
A.??? △AED???????????????????????????B.?△ABD???????????????????????????C.?△BCD???????????????????????????D.?△ACD
二、填空题
11.在正n边形中,若一个内角等于一个外角的3倍,则边数n的值是________.
12.如图,A、B、C、D为一个外角为40°的正多边形的顶点.若O为正多边形的中心,则 ∠OAD= ________.
13.如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画??,?若 AB=1 ?,则阴影部分图形的周长为________ ( ?结果保留 π) ?.
14.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是________.
15.如图,边长为2 3 cm的正六边形螺帽,中心为点O,OA垂直平分边CD,垂足为B,AB=17cm,用扳手拧动螺帽旋转90°,则点A在该过程中所经过的路径长为________cm.
三、解答题
16.如图,观察每个正多边形中 ∠α 的变化情况,解答下列问题:
……
(1)将下面的表格补充完整:
正多边形的边数
3
4
5
6
……
n
∠α 的度数
________
________
________
________
……
________
(2)根据规律,是否存在一个正 n 边形,使其中的 ∠α=20° ?若存在,写出 n 的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正 n 边形,使其中的 ∠α=21° ?若存在,写出 n 的值;若不存在,请说明理由.
17.如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
18.如图,在网格纸中,O、A都是格点,以O为圆心, OA 为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
(1)在圆①中画圆O的一个内接正六边形 ABCDEF ;
(2)在图②中画圆O的一个内接正八边形 ABCDEFGH .
19.(解决问题)已知A,B,C是同一平面上的三个点,以线段 AB , BC 为边,分别作正三角形 ABD 和正三角形 BCD' ,连接 CD , AD'
(1)如图1,当点A,B,C在同一直线上时,线段 CD 与 AD' 的大小关系是________;
(2)如图2,当A,B,C为三角形的顶点时(点A,B, D' 不在同一条直线上),判断线段 CD 与 AD' 的大小关系是否发生改变,并说明理由;
(3)(类比猜想)
已知A,B,C是同一平面上的三个点,以线段 AB , BC 为边,分别作正方形,连接 CD , AD' ,如图3和图4所示.判断线段 CD 与 AD' 的大小关系,并在图4(点A,B, D' 不在同一条直线上)中证明你的判断;
?
(4)(推广应用)
上面的这些结论能否推广到任意正多边形(不必证明)?
(5)如图5, CD 与 AD' 的大小关系是________,并写出它们分别在哪两个全等三角形中________;
(6)请在图6中连接图中两个顶点,构造处一组全等三角形,并写出这两个全等的三角形.
答案解析部分
一、单选题
1. B
考点:轴对称图形,中心对称及中心对称图形
解:第二个图形、第四个图形既是中心对称图形又是轴对称图形,共2个.
故答案为:B.
分析:根据中心对称图形以及轴对称图形的含义,判断得到答案即可。
2. D
考点:正多边形的性质
解:由题意这个正n边形的中心角=60°,
∴n= 360°60° =6
∴这个多边形是正六边形,
故答案为:D.
分析:求出正多边形的中心角即可解决问题.
3. C
考点:多边形内角与外角,正多边形的性质
解:∵一个正多边形的每个内角为150°,
∴这个正多边形的每个外角=180°-150°=30°,
∴这个正多边形的边数= 360°30° ?=12.
故答案为:C.
分析:根据多边形的一个内角和它相邻的外角互补可求得一个外角的度数,再根据多边形的外角和等于360°和正多边形的各个外角都相等可求解.
4. A
考点:圆内接正多边形
解:∵ 正六边形ABCDEF ,
∴∠BCD=180°-(360°÷6)=120°,
∵CB=CD,
∴∠CBD=180°-120°2=30°;
故答案为:A.
分析:先根据正多边形的外角和求出这个正六边形的一个内角的度数,再结合等腰三角形的性质,利用三角形的内角和定理即可求出∠CBD的度数.
5. D
考点:多边形的对角线,正多边形的性质
解:A、五条长度相等的线段首尾顺次相接所构成的图形不一定是正五边形,故本选项说法错误,不符合题意;
B、正六边形各内角都相等,但各内角都相等的六边形不一定是正六边形,故本选项说法错误,不符合题意;
C、从n边形的一个顶点出发可以引(n-3)条对角线,本选项说法错误,不符合题意;
D、n边形共有 n(n-3)2 条对角线,故本选项说法正确,符合题意.
故答案为:D.
分析:根据正多边形的定义即可判断A、B两项,根据多边形对角线的性质和条数公式即可判断C、D两项,进而可得答案.
6. D
考点:多边形内角与外角,正多边形的性质
解:设所求正n边形边数为n,?则 144°?n=(n-2)?180° ,
解得 n=10 ,
故答案为:D.
分析:利用多边形的内角和定理建立方程计算得结论.
7. D
考点:解直角三角形,正多边形的性质
解:设O是正六边形的中心,AB是正六边形的一边,OC是边心距
∵ ∠AOB=360°6=60°,OA=OB
∴△OAB是正三角形.
∴AO=AB=2a,∠OAB=60° ?
∵OC=OA?sin∠OAB= 2a·32=3a ,
∴S△OAB= 12 AB?OC= 12×2a×3a=3a2 ,
∴正六边形的面积为 6×3a2=63a2 .
故答案为::D.
分析:由题意画出图形,设O是正六边形的中心,AB是正六边形的一边,OC是边心距,由正多边形的性质可得△OAB是正三角形,解直角三角形OAC可求得OC的长,然后根据S正六边形=6×S△AOB可求解.
8. A
考点:等腰三角形的性质,正多边形的性质
解:∵正五边形ABCDE和正方形ABFG
∴∠EAB=∠E=5-2×180°5=108° , ∠GAB=90°,EA=ED,
∴∠EAD=12180°-108°=36°
∴∠BAD=∠EAB-∠EAD=108°-36°=72°,
∴∠GAD=∠GAB-∠BAD=90°-72°=18°.
故答案为:A.
分析:正多边形的内角和定理求出∠EAB,EA=ED,∠GAB的度数,再利用等腰三角形的性质及三角形内角和定理,可求出∠EAD,∠BAD的度数;然后根据∠GAD=∠GAB-∠BAD,可求出∠GAD的度数。
9. A
考点:三角形的外角性质,正多边形的性质
解:正十边形的每个内角的度数为 (10-2)×180°10=144° ,
则 ∠BAE=12×[(5-2)×180°-144°×3]=54° ,
∠ABE=12×[(6-2)×180°-144°×4]=72° ,
由三角形的外角性质得: ∠AED=∠BAE+∠ABE=126° ,
故答案为:A.
分析:根据正十边形的性质求出各内角的度数,再根据正五边形及正六边形的内角和公式分别求出∠BAE、∠ABE的度数,最后利用三角形外角的性质进行解答即可.
10. D
考点:三角形的外接圆与外心,正多边形的性质
解:因为三角形的外心到三角形的三个顶点的距离相等,所以由正六边形性质可知,点O到A,B,C,D,E的距离中,只有OA=OC=OD.
故答案为:D.
分析:根据三角形外心的性质,到三个顶点的距离相等,可以依次判断.
二、填空题
11. 8
考点:多边形内角与外角,正多边形的性质
解:设多边形的外角是x,则内角是3x.
则 x+3x=180° ,
解得 x=45° .
∴n=36045=8 .
故答案为8.
分析:本题考查了正多边形的外角与内角的知识,设外角为x,则其内角为3x , 然后利用正多边形的内角与外角互补列出方程求得x的值,然后根据多边形的外角和为 360° 求边数即可.
12. 30°
考点:三角形内角和定理,等腰三角形的性质,正多边形的性质
解:多边形的每个外角相等,且其和为 360?
据此可得多边形的边数为: 36040=9
∴ ∠AOD=3×360?9=120?
∵OA=OD
∴ ∠OAD=∠ODA=180?-∠AOD2=180?-120?2=30?
故答案为:30°.
分析:利用正多边形的边数=360°÷一个外角的度数,可求出此多边形的边数,再求出∠AOD的度数,再利用等边对等角及三角形的内角和定理求出∠OAD的度数。
13. 65π +1
考点:弧长的计算,正多边形的性质
解:∵五边形ABCDE为正五边形,AB=1,∴AB=BC=CD=DE=EA=1,∠A=∠D=108°,∴ BE? = CE? = 108180 ?πAB= 35π ,∴C阴影=?BE? +?CE? +BC= 65π +1.
故答案为: 65π +1.
分析:观察图形可知,阴影部分的周长=弧BE+弧CE+BC,根据弧长公式l=nπR180可求解.
14. 22
考点:圆内接正多边形
解:如图所示,
∵OC=2,
∴OD=2×sin30°=1;
如图所示,
∵OC=2,
∴OD=2×sin45°= 2 ;
如图所示,
∵OA=2,
∴OD=2×cos30°= 3 ,
则该三角形的三边分别为:, 2 , 3 ,
∵12+( 2 )2=( 3 )2 ,
∴该三角形是直角边,
∴该三角形的面积是: 12 ×1× 2 = 22 .
故答案为 22 .
分析:由于内接正三角形、正方形、正六边形是特殊内角的多边形,可构造直角三角形分别求出边心距的长,再由勾股定理逆定理可得该三角形是直角三角形,进而可得其面积.
15. 10π
考点:圆内接正多边形,弧长的计算
解:连接OD,OC.
∵∠DOC=60°,OD=OC,
∴△ODC是等边三角形,
∴OD=OC=DC= 23 (cm),
∵OB⊥CD,
∴BC=BD= 3 (cm),
∴OB= 3 BC=3(cm),
∵AB=17cm,
∴OA=OB+AB=20(cm),
∴点A在该过程中所经过的路径长= 90?π?20180 =10π(cm),
故答案为:10π.
分析:利用正六边形的性质求出OB的长度,进而得到OA的长度,根据弧长公式进行计算即可.
三、解答题
16. (1)60°;45°;36°;30°;180°n
(2)存在一个正 n 边形,使其中的 ∠α=20°
理由是:根据题意得: (180n)°=20° ,解得: n=9 ,
即当多边形是正九边形,能使其中的 ∠α=20° ;
(3)不存在,理由如下:
假设存在正 n 边形使得 ∠α=21° ,得 ∠α=21°=(180n)° ,
解得: n=847 ,与 n 是正整数矛盾,
所以不存在正 n 边形使得 ∠α=21° .
考点:多边形内角与外角,圆内接正多边形
解:(1)填表如下:
正多边形的边数
3
4
5
6
……
n
∠α 的度数
60°
45°
36°
30°
……
(180n)°
60° , 45° , 36° , 30° , 180°n ;(可以观察归纳出来,也可以计算出来).
分析:(1)首先根据多边形的内角公式:(n-2)×180°,将n=3、4、5、6、8、12代入公式分别计算出各多边形的内角和;然后再根据多边形的外角和为360°,即可得到各多边形的内角和,进而完成表格.(2)依据题意得∠α=20°= 180°n ,即可求出n的值。(3)依据题意∠α=21°= 180°n ,求出n的值是否为正整数即可.
17. 解:如图1,连接OB、OC,过O作OD⊥AB于D,
∵⊙O是正三角形ABC的外接圆,
∴∠AOB= 360°3 =120°,
∵OA=OB,
∴∠AOD=∠BOD=60°,
在Rt△ADO中,AO=R,AD=R×sin60°= 32 R,OD=Rcos60°= 12 R,
∵OD⊥AB,
∴AB=2AD= 3 R,
∴正△ABC的周长是3AB=3 3 R;面积是3× 12 AB×OD=3× 12 × 3 R× 12 R= 34 R2;
如图2,连接OA、OB、OD,
∵⊙O是正方形ABCD的外接圆,
∴∠COD= 360°4 =90°,
∵OD=OC=R,由勾股定理得;CD= R2+R2 = 2 R,
∴正方形ABCD的周长为4× 2 R=4 2 R,面积为 2 R× 2 R=2R2 .
考点:圆内接正多边形,解直角三角形
分析: 如图1,连接OB、OC,过O作OD⊥AB于D, 利用正多边形和圆的性质,可得出∠AOD=60°,由OA=R,利用解直角三角形分别求出AD、OD,即可求出AB的长,继而可求出△ABC的周长,再由△ABC的面积=3×△AOB的面积,即可求解;如图2, 连接OA、OB、OD,利用正方形的性质,可知∠COD=90°,OC=OD=R,利用勾股定理求出CD,然后求出正方形ABCD的周长和面积。
?18. (1)解:设AO的延长线与圆交于点D,
根据圆的内接正六边形的性质,点D即为正六边形的一个顶点,且正六边形的边长等于圆的半径,即OB=AB,故在图中找到AO的中垂线与圆的交点即为正六边形的顶点B和F;同理:在图中找到OD的中垂线与圆的交点即为正六边形的顶点C和E,连接AB、BC、CD、DE、EF、FA,如图①,正六边形 ABCDEF 即为所求.
(2)解:圆的内接八边形的中心角为360°÷8=45°,而正方形的对角线与边的夹角也为45°
∴在如②图所示的正方形OMNP中,连接对角线ON并延长,交圆于点B,此时∠AON=45°;∵∠NOP=45°,
∴OP的延长线与圆的交点即为点C
同理,即可确定点D、E、F、G、H的位置,顺次连接,
如图②,正八边形 ABCDEFGH 即为所求.
考点:正方形的性质,圆内接正多边形,正多边形的性质
分析:(1)设AO的延长线与圆交于点D,根据正六边形的性质,点D即为正六边形的一个顶点,且正六边形的边长等于圆的半径,根据垂直平分线的性质即可确定其它的顶点;(2)先求出内接八边形的中心角,然后根据正方形的性质即可找到各个顶点.
19. (1)解:相等
(2)解:线段 CD 与 AD' 的大小关系没有改变,理由如下:
∵△ABD、△BCD’是等边三角形,
∴AB=BD,BD’=BC, ∠ABD=∠CBD'=60°
∵ ∠ABD'=∠ABC+∠CBD' , ∠DBC=∠ABC+∠ABD
∴ ∠ABD'=∠DBC
∴△ABD’≌△DBC(SAS)
∴ CD = AD'
(3)解:在如图3和图4.判断线段 CD 与 AD' 的大小关系为相等,理由如下:
∵四边形ABDE、四边形BCD’E’是正方形,
∴AB=BD,BD’=BC, ∠ABD=∠CBD'=90°
∵ ∠ABD'=∠ABD+∠DBD' , ∠DBC=∠D'BC+∠DBD'
∴ ∠ABD'=∠DBC
∴△ABD’≌△DBC(SAS)
∴ CD = AD'
故线段 CD 与 AD' 的大小关系为相等;
(4)能推广到任意正多边形
(5)相等;△ABD’≌△DBC
(6)解:如图,连接GD’,
∵六边形ABDEFG、六边形ACG’F’E’ D’是正方形,
∴AB=AG,AD’=AC, ∠GAB=∠CAD'=120°
∵ ∠GAD'=∠GAB-∠BAD' , ∠BAC=∠D'AC-∠BAD'
∴ ∠GAD'=∠BAC
∴△GAD’≌△BAC(SAS)
故答案为△GAD’≌△BAC.
考点:三角形全等及其性质,正多边形的性质
解:(1)∵△ABD、△BCD’是等边三角形,
∴AB=BD,BD’=BC, ∠ABD=∠CBD'=60°
∵ ∠ABD'=∠ABD+∠DBD' , ∠DBC=∠D'BC+∠DBD'
∴ ∠ABD'=∠DBC
∴△ABD’≌△DBC(SAS)
∴ CD = AD'
故答案为:相等;(4)根据题意及图形的特点同理可得△ABD’≌△DBC,则 CD = AD'
故线段 CD 与 AD' 的大小关系为相等,能推广到任意正多边形;(5)∵五边形ABDEF、五边形BCF’E’ D’是正方形,
∴AB=BD,BD’=BC, ∠ABD=∠CBD'=108°
∵ ∠ABD'=∠ABD+∠DBD' , ∠DBC=∠D'BC+∠DBD'
∴ ∠ABD'=∠DBC
∴△ABD’≌△DBC(SAS)
∴ CD = AD'
故答案为:相等;△ABD’≌△DBC;
分析:(1)根据正三角形的性质证明△ABD’≌△DBC,即可求解;(2)同理证明△ABD’≌△DBC,即可求解;(3)根据正方形的性质同理证明△ABD’≌△DBC,即可求解;(4)根据题意及图形的特点可知这些结论能否推广到任意正多边形;(5)根据正五边形的性质同理证明△ABD’≌△DBC,即可求解;(6)连接GD’,证明△ABC≌△AGD’即可求解.
、
