3.1 投影同步练习(含解析)
图片预览



文档简介
初中数学湘教版九年级下册3.1投影 同步练习
一、单选题
1.如图所示是一天中不同时刻直立的灯杆在阳光下形成的影长,规定各图向右为正东方向,将各图按时间顺序排列正确的是(?? )
A.?②④①③???????????????????????????B.?①④③②???????????????????????????C.?②④③①???????????????????????????D.?①③②④
2.如图,水杯的杯口与投影面平行,投影线的几方向如箭头所示,它的正投影是(??? )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
3.如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是(???? )
A.?③—④—①—②????????????B.?②—①—④—③????????????C.?④—①—②—③????????????D.?④—①—③—②
4.下列投影现象属于平行投影的是(?? )
A.?手电筒发出的光线所形成的投影?????????????????????????B.?太阳光发出的光线所形成的投影
C.?路灯发出的光线所形成的投影?????????????????????????????D.?台灯发出的光线所形成的投影
5.小明在太阳光下观察矩形木板的影子,不可能是(?? )
A.?平行四边形?????????????????????????????????B.?矩形?????????????????????????????????C.?线段?????????????????????????????????D.?梯形
6.下列光线所形成的投影不是中心投影的是(?? )
A.?太阳光线???????????????????????B.?台灯的光线???????????????????????C.?手电筒的光线???????????????????????D.?路灯的光线
7.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为(?? )
A.?3???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
8.某数学兴趣小组利用阳光下的影子测量建筑物的高度,已知小明的身高1.5m,测量其影子为1.2m,建筑物的影长为14m,则建筑物的高是(?? )m.
A.?16.5???????????????????????????????????????B.?17???????????????????????????????????????C.?17.5???????????????????????????????????????D.?18
9.在同一时刻的阳光下,身高1.6 m的小强的影长是1.2 m,旗杆的影长是15 m,则旗杆的高为(? )
A.?16 m???????????????????????????????????B.?18 m???????????????????????????????????C.?20 m???????????????????????????????????D.?22 m
10.如图,在离某围端 AB 的6米处有一棵树 CD ,在某时刻2米长的竹竿垂直地面,太阳光下的影长为3米,此时,树的影子有一部分映在地面上,还有一部分影子映在墙上 AE 处,墙上的影高为4米,那么这棵树高约为(?? )
A.?6???????????????????????????????????????????B.?8???????????????????????????????????????????C.?9???????????????????????????????????????????D.?10
二、填空题
11.一天下午,小红先参加了校运动会女子 200m 比赛,然后又参加了女子 400m 比赛,摄影师在同一位置拍摄了她参加这两场比赛的照片如图所示,则小红参加 200m 比赛的照片是________.(填“图1”或“图2”)
12.地面上有一支蜡烛,蜡烛前面有一面墙,王涛同学在蜡烛与墙之间运动,则他在墙上的投影长度随着他离墙的距离变小而________(增大、变小)
13.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为________m.
14.墙壁CD上D处有一盏灯(如图),小明站在A处测得他的影长与身长相等,都为1.6m,他向墙壁走1m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD=________.
15.《孙子算经》是我国古代重要的数学著作,成书于约一千五百年前,其中有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问杆长几何?”歌谣的意思是:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五,同时立一根一尺五的小标杆,它的影长五寸(提示:仗和尺是古代的长度单位,1丈=10尺,1尺=10寸),可以求出竹竿的长为________尺.
三、解答题
16.如图,两幢楼高AB=CD=30m,两楼间的距离AC=24m,当太阳光线与水平线的夹角为30°时,求甲楼投在乙楼上的影子的高度.(结果精确到0.01, 3 ≈1.732, 2 ≈1.414)
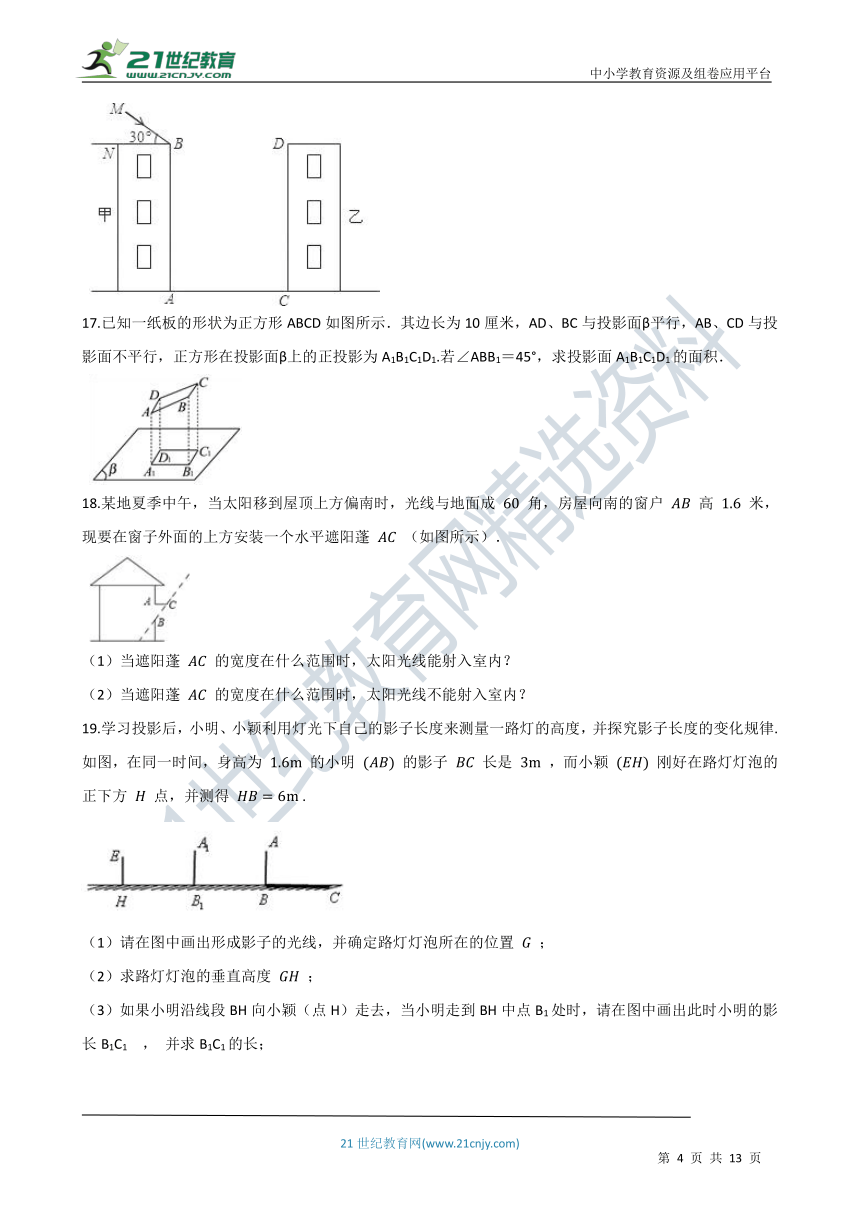
17.已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
18.某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成 60 角,房屋向南的窗户 AB 高 1.6 米,现要在窗子外面的上方安装一个水平遮阳蓬 AC (如图所示).
(1)当遮阳蓬 AC 的宽度在什么范围时,太阳光线能射入室内?
(2)当遮阳蓬 AC 的宽度在什么范围时,太阳光线不能射入室内?
19.学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为 1.6m 的小明 (AB) 的影子 BC 长是 3m ,而小颖 (EH) 刚好在路灯灯泡的正下方 H 点,并测得 HB=6m .
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置 G ;
(2)求路灯灯泡的垂直高度 GH ;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,请在图中画出此时小明的影长B1C1 , 并求B1C1的长;
答案解析部分
一、单选题
1. B
考点:平行投影
解:太阳从东方升起最后从西面落下,木杆的影子开始时应该在西面,随着时间的变化影子逐渐的向北偏西,北偏东,正东方向的顺序移动,故它们按时间先后顺序进行排列为:①④③②,
故答案为:B.
分析:太阳从东方升起最后从西面落下,木杆的影子开始时应该在西面,随着时间的变化影子逐渐的向北偏西,北偏东,正东方向的顺序移动可得结果.
2. D
考点:平行投影
解:依题意,光线是垂直照下的,它的正投影图有圆形,只有D符合,
故答案为:D.
分析:由于水杯的杯口与投影面平行,即与光线垂直,从而可知它的正投影有圆,据此逐一判断即可.
3. B
考点:中心投影
解:众所周知,影子方向的变化是上午时朝向西边,中午时朝向北边,下午时朝向东边;
影子长短的变化是由长变短再变长,结合方向和长短的变化即可得出答案
故答案为:B
分析:根据一天中影子的长短和方向判断即可.
4. B
考点:平行投影
解:因为投影线交于一点的投影为中心投影,投影线相互平行的投影称为平行投影,
所以A,C,D都属于中心投影,只有B属于平行投影.
故答案为:B.
分析:投影线交于一点的投影为中心投影,投影线相互平行的投影称为平行投影,由慨念进行逐一判断即可.
5. D
考点:平行投影
解:A.将木框倾斜放置形成的影子为平行四边形,故该选项不符合题意,
B.将矩形木框与地面平行放置时,形成的影子为矩形,故该选项不符合题意,
C.将矩形木框立起与地面垂直放置时,形成的影子为线段,
D.∵由物体同一时刻物高与影长成比例,且矩形对边相等,梯形两底不相等,
∴得到投影不可能是梯形,故该选项符合题意,
故答案为:D.
分析:根据平行投影的特点可确定矩形木板与地面平行且与光线垂直时所成的投影为矩形;当矩形木板与光线方向平行且与地面垂直时所成的投影为一条线段;除以上两种情况矩形在地面上所形成的投影均为平行四边形,据此逐一判断即可得答案.
6. A
考点:中心投影
解:A.太阳距离地球很远,我们认为是平行光线,因此不是中心投影.
B.台灯的光线是由台灯光源发出的光线,是中心投影;
C.手电筒的光线是由手电筒光源发出的光线,是中心投影;
D.路灯的光线是由路灯光源发出的光线,是中心投影.
所以,只有A不是中心投影.
故答案为:A.
分析:利用中心投影(光由一点向外散射形成的投影叫做中心投影)和平行投影(由平行光线形成的投影是平行投影)的定义即可判断出.
7. C
考点:相似三角形的判定与性质,中心投影
解:延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图
∵P(2,2),A(0,1),B(3,1).
∴PD=1,PE=2,AB=3,
∵AB∥A′B′,
∴△PAB∽△PA′B′,
∴ ABA'B'=ADAE ,即 3A'B'=12
∴A′B′=6,
故答案为:C.
分析:利用中心投影,延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,证明△PAB∽△PA′B′,然后利用相似比可求出A'B'的长.
8. C
考点:平行投影
解:设建筑物的高为x米,
根据题意得: x1.5=141.2 ,
解得: x=17.5 ,
故答案为:C.
分析:根据同一时刻同一地点的物高与影长成比例即可求得答案.
9. C
考点:平行投影
解:设旗杆高度为x米,有1.6:1.2=x:15,
解得:x=20.
故答案为:C.
分析:设旗杆高度为x米,则利用再同一时刻物高与影长的比相等列出比例式求解即可。
10. B
考点:平行投影
解:过点A作AF∥DE交CD于点F,
则DF=AE=4m,△CAF∽△C′CD′.
∴D′C′:C′C=CF:CA,即2:3=CF:6.
∴CF=4.
∴DC=4+4=8(m).
即:这棵树高8m.
故答案为:B.
分析:因为在同一时刻同一地点任何物体的高与其影子长的比值相同,利用竹竿这个参照物就可以求出图中的CF.CA是CF的影子,然后加上AE加上树高即可.
二、填空题
11. 图2
考点:平行投影
解:根据平行投影的规律:从早晨到傍晚物体的指向是:西-西北-北-东北-东,影长由长变短,再变长;当太阳光在中午时,所产生的影子就比较短,当太阳光在上午或者下午时,所产生的影子就比较长,所以这位同学参加200米比赛的照片是图2.
故答案为:图2.
分析:通过比较人的影子的方向可判断时间的先后顺序.
12. 变小
考点:中心投影
解:?距离墙越近,影长越短,距离墙越远,影长越长,则他在墙上的投影长度随着他离墙的距离变小而变小.
故答案为:变小.
分析:一般情况下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度短.
13. 2.4
考点:平行投影
解:如图,过N点作ND⊥PQ于D,
?
∴ BCAB=DNQD ,
又∵AB=2,BC=1.5,DN=PM=1.2, NM=0.8,
∴ 1.52=1.2QD ,
∴QD=1.6,
∴PQ=QD+DP=QD+NM=1.6+0.8=2.4(m).
故答案为:2.4.
分析:过N点作ND⊥PQ于D,先根据同一时刻物高与影长成正比求出QD的影长,再求出PQ即可.
14. 6415 m
考点:中心投影
解:如图:
根据题意得:BG=AF=AE=1.6m,AB=1m,
∵BG∥AF∥CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.6)m,AC=(x+1)m,
∴ 1.6x+2.6=1.6y , 1x+1=1.6y
解得:x= 53 , y= 6415 ,
∴CD= 6415 m.
∴灯泡与地面的距离为 6415 米,
故答案为 6415 m.
分析:根据题意找平行线得到△EAF∽△ECD,△ABG∽△ACD,再利用相似三角形的性质得到比例式求解即可。
15. 45
考点:平行投影
解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴ x15=0.51.5 ,解得x=45(尺).
故答案为:45.
分析:根据同一时刻物高与影长成正比可得出结论.
三、解答题
16. 解:如图,延长MB交CD于E,连接BD,
由于AB=CD=30m,AB⊥AC,CD⊥AC,
∴四边形ACDB是矩形,
∴NB和BD在同一直线上,∠DBE=∠MBN=30°
∴AC=BD=24m,∠BDE=90°,
在Rt△BED中tan30°= DEBD ,
DE=BD?tan30°=24× 33=83 ,
∴CE=30﹣8 3 ≈16.14(m),
答:甲楼投到乙楼影子高度是16.14m.
考点:锐角三角函数的定义,特殊角的三角函数值,平行投影
分析: 如图,延长MB交CD于E,连接BD, 首先判断出 四边形ACDB是矩形, 根据矩形的性质得出 AC=BD=24m,∠BDE=90°, 进而根据平角的定义判断出 NB和BD在同一直线上,根据对顶角相等得出∠DBE=∠MBN=30° , 在Rt△BED中 ,根据正切函数的定义,及特殊锐角三角函数值,由 DE=BD?tan30° 算出DE,从而得出答案。
17. 解:如图所示,过A作AH⊥BB1于H,
∵∠ABB1=45°,
∴△ABH是等腰直角三角形,
∴AH=AB·cos45°=10× 22 =5 2 ?(厘米),
∴A1B1=AH=5 2 (厘米),
∵A1D1=AD=10(厘米),
∴SA1B1C1D1?=A1B1×A1D1=52×10=502(平方厘米)
考点:锐角三角函数的定义,平行投影
分析: 如图所示,过A作AH⊥BB1于H, 首先很容易得出 △ABH是等腰直角三角形, 根据余弦函数的定义及特殊锐角三角函数值,由 AH=AB·cos45°即可算出AH的长,根据矩形的性质得出 A1B1=AH ,根据平行投影的性质得出 A1D1=AD ,然后滚局矩形面积的计算方法即可算出答案。
18. (1)解:在 △ABC 组成 ∠ABC 是 30° 的直角三角形.
∴ AC=AB?tan∠ABC=33AB=8153 (米).
当遮阳蓬 AC 的宽度小于等于 8153 米时,太阳光线能射入室内
(2)解:当遮阳蓬 AC 的宽度大于 8153 米时,太阳光线不能射入室内.
考点:锐角三角函数的定义,平行投影
分析:(1)根据题意直角三角形ABC中,∠ABC=30°,根据正切函数的定义及特殊锐角三角函数值,由AC=AB·tan∠ABC即可算出AC的长,从而得出当遮阳蓬 AC 的宽度小于等于计算的值的时候 太阳光线能射入室内 ;
(2)刚好是与(1)小题相反的结论。
19. (1)解:如图,连接CA,HE并延长相交于点G,即为所求路灯灯泡的位置,作出图形即可;
(2)解:由题意得:易得△ABC∽△GHC,
∴ ABGH=BCHC ,
∴ 1.6GH=36+3 ,
解得:GH=4.8,
答:路灯灯泡的垂直高度GH是4.8m;
(3)解:连接G A1 延长交HC于点 C1 ,则 B1 C1 即为小明的影子,在(1)中作图即得,与(2)类似,易证△ A1B1C1 ∽△GH C1 ,
∴ A1B1GH=B1C1HC1 ,
设 B1C1 长为xm, B1 为HB的中点,
则 1.64.8=xx+3 ,
解得:x= 32 ,
即 B1C1 = 32 m,
答:小明的影子 B1C1 的长是 32 m;
考点:相似三角形的判定与性质,中心投影
分析:(1)根据题意,连接CA,HE并延长相交于点G,即为所求路灯灯泡的位置,作出图形即可;(2)根据题意得到△ABC∽△GHC ,根据相似三角形的性质得到 ABGH=BCHC ,代入即可求出答案;
(3)与(2)类似得到△ A1B1C1 ∽△GH C1 ,根据相似三角形的性质推出 A1B1GH=B1C1HC1 ,代入即可求出答案,连接G A1 延长交HC于点 C1 ,即得小明的影子.
一、单选题
1.如图所示是一天中不同时刻直立的灯杆在阳光下形成的影长,规定各图向右为正东方向,将各图按时间顺序排列正确的是(?? )
A.?②④①③???????????????????????????B.?①④③②???????????????????????????C.?②④③①???????????????????????????D.?①③②④
2.如图,水杯的杯口与投影面平行,投影线的几方向如箭头所示,它的正投影是(??? )
A.???????????????????????????B.???????????????????????????C.???????????????????????????D.?
3.如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是(???? )
A.?③—④—①—②????????????B.?②—①—④—③????????????C.?④—①—②—③????????????D.?④—①—③—②
4.下列投影现象属于平行投影的是(?? )
A.?手电筒发出的光线所形成的投影?????????????????????????B.?太阳光发出的光线所形成的投影
C.?路灯发出的光线所形成的投影?????????????????????????????D.?台灯发出的光线所形成的投影
5.小明在太阳光下观察矩形木板的影子,不可能是(?? )
A.?平行四边形?????????????????????????????????B.?矩形?????????????????????????????????C.?线段?????????????????????????????????D.?梯形
6.下列光线所形成的投影不是中心投影的是(?? )
A.?太阳光线???????????????????????B.?台灯的光线???????????????????????C.?手电筒的光线???????????????????????D.?路灯的光线
7.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为(?? )
A.?3???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
8.某数学兴趣小组利用阳光下的影子测量建筑物的高度,已知小明的身高1.5m,测量其影子为1.2m,建筑物的影长为14m,则建筑物的高是(?? )m.
A.?16.5???????????????????????????????????????B.?17???????????????????????????????????????C.?17.5???????????????????????????????????????D.?18
9.在同一时刻的阳光下,身高1.6 m的小强的影长是1.2 m,旗杆的影长是15 m,则旗杆的高为(? )
A.?16 m???????????????????????????????????B.?18 m???????????????????????????????????C.?20 m???????????????????????????????????D.?22 m
10.如图,在离某围端 AB 的6米处有一棵树 CD ,在某时刻2米长的竹竿垂直地面,太阳光下的影长为3米,此时,树的影子有一部分映在地面上,还有一部分影子映在墙上 AE 处,墙上的影高为4米,那么这棵树高约为(?? )
A.?6???????????????????????????????????????????B.?8???????????????????????????????????????????C.?9???????????????????????????????????????????D.?10
二、填空题
11.一天下午,小红先参加了校运动会女子 200m 比赛,然后又参加了女子 400m 比赛,摄影师在同一位置拍摄了她参加这两场比赛的照片如图所示,则小红参加 200m 比赛的照片是________.(填“图1”或“图2”)
12.地面上有一支蜡烛,蜡烛前面有一面墙,王涛同学在蜡烛与墙之间运动,则他在墙上的投影长度随着他离墙的距离变小而________(增大、变小)
13.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ的长度为________m.
14.墙壁CD上D处有一盏灯(如图),小明站在A处测得他的影长与身长相等,都为1.6m,他向墙壁走1m到B处时发现影子刚好落在A点,则灯泡与地面的距离CD=________.
15.《孙子算经》是我国古代重要的数学著作,成书于约一千五百年前,其中有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问杆长几何?”歌谣的意思是:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五,同时立一根一尺五的小标杆,它的影长五寸(提示:仗和尺是古代的长度单位,1丈=10尺,1尺=10寸),可以求出竹竿的长为________尺.
三、解答题
16.如图,两幢楼高AB=CD=30m,两楼间的距离AC=24m,当太阳光线与水平线的夹角为30°时,求甲楼投在乙楼上的影子的高度.(结果精确到0.01, 3 ≈1.732, 2 ≈1.414)
17.已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
18.某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成 60 角,房屋向南的窗户 AB 高 1.6 米,现要在窗子外面的上方安装一个水平遮阳蓬 AC (如图所示).
(1)当遮阳蓬 AC 的宽度在什么范围时,太阳光线能射入室内?
(2)当遮阳蓬 AC 的宽度在什么范围时,太阳光线不能射入室内?
19.学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为 1.6m 的小明 (AB) 的影子 BC 长是 3m ,而小颖 (EH) 刚好在路灯灯泡的正下方 H 点,并测得 HB=6m .
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置 G ;
(2)求路灯灯泡的垂直高度 GH ;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,请在图中画出此时小明的影长B1C1 , 并求B1C1的长;
答案解析部分
一、单选题
1. B
考点:平行投影
解:太阳从东方升起最后从西面落下,木杆的影子开始时应该在西面,随着时间的变化影子逐渐的向北偏西,北偏东,正东方向的顺序移动,故它们按时间先后顺序进行排列为:①④③②,
故答案为:B.
分析:太阳从东方升起最后从西面落下,木杆的影子开始时应该在西面,随着时间的变化影子逐渐的向北偏西,北偏东,正东方向的顺序移动可得结果.
2. D
考点:平行投影
解:依题意,光线是垂直照下的,它的正投影图有圆形,只有D符合,
故答案为:D.
分析:由于水杯的杯口与投影面平行,即与光线垂直,从而可知它的正投影有圆,据此逐一判断即可.
3. B
考点:中心投影
解:众所周知,影子方向的变化是上午时朝向西边,中午时朝向北边,下午时朝向东边;
影子长短的变化是由长变短再变长,结合方向和长短的变化即可得出答案
故答案为:B
分析:根据一天中影子的长短和方向判断即可.
4. B
考点:平行投影
解:因为投影线交于一点的投影为中心投影,投影线相互平行的投影称为平行投影,
所以A,C,D都属于中心投影,只有B属于平行投影.
故答案为:B.
分析:投影线交于一点的投影为中心投影,投影线相互平行的投影称为平行投影,由慨念进行逐一判断即可.
5. D
考点:平行投影
解:A.将木框倾斜放置形成的影子为平行四边形,故该选项不符合题意,
B.将矩形木框与地面平行放置时,形成的影子为矩形,故该选项不符合题意,
C.将矩形木框立起与地面垂直放置时,形成的影子为线段,
D.∵由物体同一时刻物高与影长成比例,且矩形对边相等,梯形两底不相等,
∴得到投影不可能是梯形,故该选项符合题意,
故答案为:D.
分析:根据平行投影的特点可确定矩形木板与地面平行且与光线垂直时所成的投影为矩形;当矩形木板与光线方向平行且与地面垂直时所成的投影为一条线段;除以上两种情况矩形在地面上所形成的投影均为平行四边形,据此逐一判断即可得答案.
6. A
考点:中心投影
解:A.太阳距离地球很远,我们认为是平行光线,因此不是中心投影.
B.台灯的光线是由台灯光源发出的光线,是中心投影;
C.手电筒的光线是由手电筒光源发出的光线,是中心投影;
D.路灯的光线是由路灯光源发出的光线,是中心投影.
所以,只有A不是中心投影.
故答案为:A.
分析:利用中心投影(光由一点向外散射形成的投影叫做中心投影)和平行投影(由平行光线形成的投影是平行投影)的定义即可判断出.
7. C
考点:相似三角形的判定与性质,中心投影
解:延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图
∵P(2,2),A(0,1),B(3,1).
∴PD=1,PE=2,AB=3,
∵AB∥A′B′,
∴△PAB∽△PA′B′,
∴ ABA'B'=ADAE ,即 3A'B'=12
∴A′B′=6,
故答案为:C.
分析:利用中心投影,延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,证明△PAB∽△PA′B′,然后利用相似比可求出A'B'的长.
8. C
考点:平行投影
解:设建筑物的高为x米,
根据题意得: x1.5=141.2 ,
解得: x=17.5 ,
故答案为:C.
分析:根据同一时刻同一地点的物高与影长成比例即可求得答案.
9. C
考点:平行投影
解:设旗杆高度为x米,有1.6:1.2=x:15,
解得:x=20.
故答案为:C.
分析:设旗杆高度为x米,则利用再同一时刻物高与影长的比相等列出比例式求解即可。
10. B
考点:平行投影
解:过点A作AF∥DE交CD于点F,
则DF=AE=4m,△CAF∽△C′CD′.
∴D′C′:C′C=CF:CA,即2:3=CF:6.
∴CF=4.
∴DC=4+4=8(m).
即:这棵树高8m.
故答案为:B.
分析:因为在同一时刻同一地点任何物体的高与其影子长的比值相同,利用竹竿这个参照物就可以求出图中的CF.CA是CF的影子,然后加上AE加上树高即可.
二、填空题
11. 图2
考点:平行投影
解:根据平行投影的规律:从早晨到傍晚物体的指向是:西-西北-北-东北-东,影长由长变短,再变长;当太阳光在中午时,所产生的影子就比较短,当太阳光在上午或者下午时,所产生的影子就比较长,所以这位同学参加200米比赛的照片是图2.
故答案为:图2.
分析:通过比较人的影子的方向可判断时间的先后顺序.
12. 变小
考点:中心投影
解:?距离墙越近,影长越短,距离墙越远,影长越长,则他在墙上的投影长度随着他离墙的距离变小而变小.
故答案为:变小.
分析:一般情况下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度短.
13. 2.4
考点:平行投影
解:如图,过N点作ND⊥PQ于D,
?
∴ BCAB=DNQD ,
又∵AB=2,BC=1.5,DN=PM=1.2, NM=0.8,
∴ 1.52=1.2QD ,
∴QD=1.6,
∴PQ=QD+DP=QD+NM=1.6+0.8=2.4(m).
故答案为:2.4.
分析:过N点作ND⊥PQ于D,先根据同一时刻物高与影长成正比求出QD的影长,再求出PQ即可.
14. 6415 m
考点:中心投影
解:如图:
根据题意得:BG=AF=AE=1.6m,AB=1m,
∵BG∥AF∥CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.6)m,AC=(x+1)m,
∴ 1.6x+2.6=1.6y , 1x+1=1.6y
解得:x= 53 , y= 6415 ,
∴CD= 6415 m.
∴灯泡与地面的距离为 6415 米,
故答案为 6415 m.
分析:根据题意找平行线得到△EAF∽△ECD,△ABG∽△ACD,再利用相似三角形的性质得到比例式求解即可。
15. 45
考点:平行投影
解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴ x15=0.51.5 ,解得x=45(尺).
故答案为:45.
分析:根据同一时刻物高与影长成正比可得出结论.
三、解答题
16. 解:如图,延长MB交CD于E,连接BD,
由于AB=CD=30m,AB⊥AC,CD⊥AC,
∴四边形ACDB是矩形,
∴NB和BD在同一直线上,∠DBE=∠MBN=30°
∴AC=BD=24m,∠BDE=90°,
在Rt△BED中tan30°= DEBD ,
DE=BD?tan30°=24× 33=83 ,
∴CE=30﹣8 3 ≈16.14(m),
答:甲楼投到乙楼影子高度是16.14m.
考点:锐角三角函数的定义,特殊角的三角函数值,平行投影
分析: 如图,延长MB交CD于E,连接BD, 首先判断出 四边形ACDB是矩形, 根据矩形的性质得出 AC=BD=24m,∠BDE=90°, 进而根据平角的定义判断出 NB和BD在同一直线上,根据对顶角相等得出∠DBE=∠MBN=30° , 在Rt△BED中 ,根据正切函数的定义,及特殊锐角三角函数值,由 DE=BD?tan30° 算出DE,从而得出答案。
17. 解:如图所示,过A作AH⊥BB1于H,
∵∠ABB1=45°,
∴△ABH是等腰直角三角形,
∴AH=AB·cos45°=10× 22 =5 2 ?(厘米),
∴A1B1=AH=5 2 (厘米),
∵A1D1=AD=10(厘米),
∴SA1B1C1D1?=A1B1×A1D1=52×10=502(平方厘米)
考点:锐角三角函数的定义,平行投影
分析: 如图所示,过A作AH⊥BB1于H, 首先很容易得出 △ABH是等腰直角三角形, 根据余弦函数的定义及特殊锐角三角函数值,由 AH=AB·cos45°即可算出AH的长,根据矩形的性质得出 A1B1=AH ,根据平行投影的性质得出 A1D1=AD ,然后滚局矩形面积的计算方法即可算出答案。
18. (1)解:在 △ABC 组成 ∠ABC 是 30° 的直角三角形.
∴ AC=AB?tan∠ABC=33AB=8153 (米).
当遮阳蓬 AC 的宽度小于等于 8153 米时,太阳光线能射入室内
(2)解:当遮阳蓬 AC 的宽度大于 8153 米时,太阳光线不能射入室内.
考点:锐角三角函数的定义,平行投影
分析:(1)根据题意直角三角形ABC中,∠ABC=30°,根据正切函数的定义及特殊锐角三角函数值,由AC=AB·tan∠ABC即可算出AC的长,从而得出当遮阳蓬 AC 的宽度小于等于计算的值的时候 太阳光线能射入室内 ;
(2)刚好是与(1)小题相反的结论。
19. (1)解:如图,连接CA,HE并延长相交于点G,即为所求路灯灯泡的位置,作出图形即可;
(2)解:由题意得:易得△ABC∽△GHC,
∴ ABGH=BCHC ,
∴ 1.6GH=36+3 ,
解得:GH=4.8,
答:路灯灯泡的垂直高度GH是4.8m;
(3)解:连接G A1 延长交HC于点 C1 ,则 B1 C1 即为小明的影子,在(1)中作图即得,与(2)类似,易证△ A1B1C1 ∽△GH C1 ,
∴ A1B1GH=B1C1HC1 ,
设 B1C1 长为xm, B1 为HB的中点,
则 1.64.8=xx+3 ,
解得:x= 32 ,
即 B1C1 = 32 m,
答:小明的影子 B1C1 的长是 32 m;
考点:相似三角形的判定与性质,中心投影
分析:(1)根据题意,连接CA,HE并延长相交于点G,即为所求路灯灯泡的位置,作出图形即可;(2)根据题意得到△ABC∽△GHC ,根据相似三角形的性质得到 ABGH=BCHC ,代入即可求出答案;
(3)与(2)类似得到△ A1B1C1 ∽△GH C1 ,根据相似三角形的性质推出 A1B1GH=B1C1HC1 ,代入即可求出答案,连接G A1 延长交HC于点 C1 ,即得小明的影子.
