2021年人教版八年级下册17.1《勾股定理》同步培优卷(Word版 含解析)
文档属性
| 名称 | 2021年人教版八年级下册17.1《勾股定理》同步培优卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 290.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 09:35:14 | ||
图片预览



文档简介
2021年人教版八年级下册17.1《勾股定理》同步培优卷
一.选择题
1.如图所示,点B,D在数轴上,OB=3,OD=BC=1,∠OBC=90°,以D为圆心,DC长为半径画弧,与数轴正半轴交于点A,则点A表示的实数是( )
A. B.+1 C.﹣1 D.不能确定
2.如图,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3.若S1=9,S2=16,则S3的值为( )
A.7 B.10 C.20 D.25
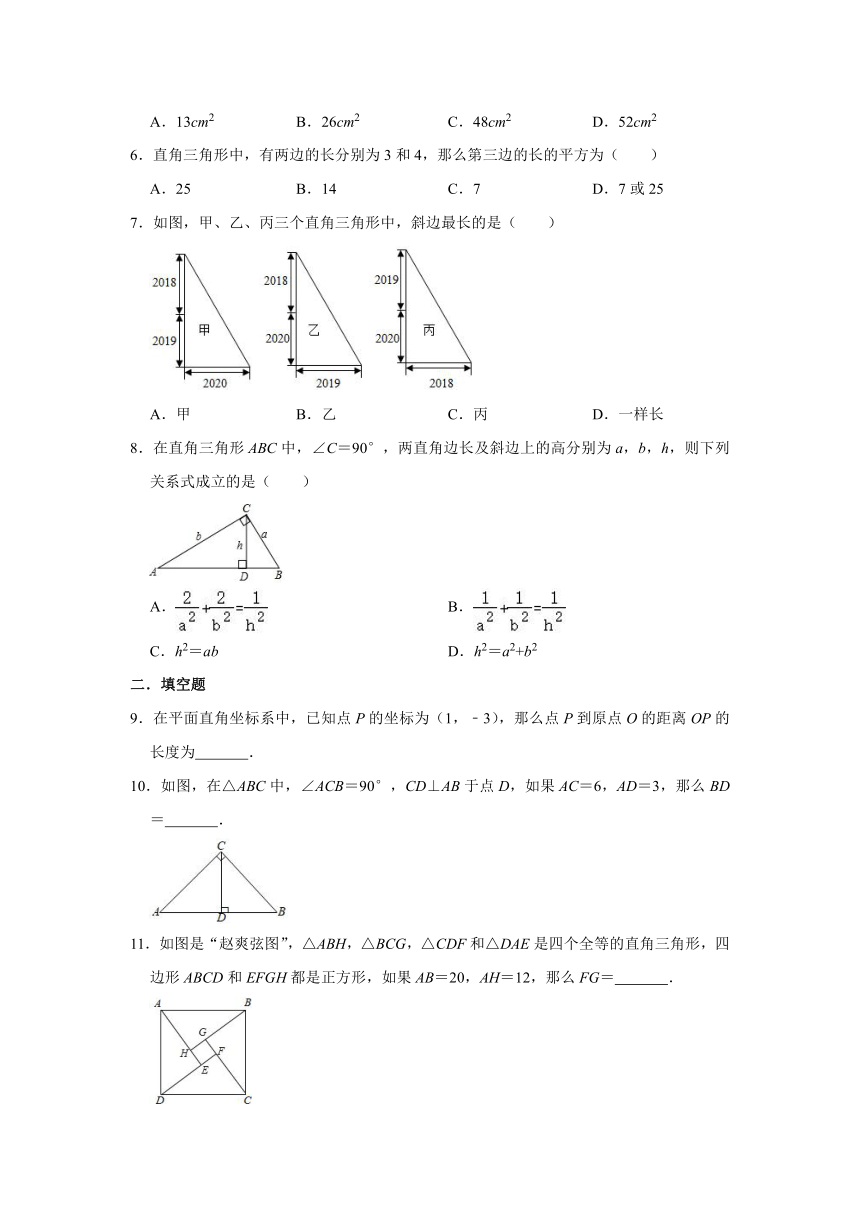
3.如图,在行距、列距都是1的的4×4方格网中,将任意连接两个格点的线段称作“格点线”,则“格点线”的长度不可能等于( )
A. B. C. D.
4.如图,OC平分∠AOB,点P是OC上一点,PM⊥OB于点M,点N是射线OA上的一个动点若OM=4,OP=5,则PN的最小值为( )
A.2 B.3 C.4 D.5
5.已知Rt△ABC中,∠C=90°.若a+b=14cm,c=12cm,则Rt△ABC的面积是( )
A.13cm2 B.26cm2 C.48cm2 D.52cm2
6.直角三角形中,有两边的长分别为3和4,那么第三边的长的平方为( )
A.25 B.14 C.7 D.7或25
7.如图,甲、乙、丙三个直角三角形中,斜边最长的是( )
A.甲 B.乙 C.丙 D.一样长
8.在直角三角形ABC中,∠C=90°,两直角边长及斜边上的高分别为a,b,h,则下列关系式成立的是( )
A. B.
C.h2=ab D.h2=a2+b2
二.填空题
9.在平面直角坐标系中,已知点P的坐标为(1,﹣3),那么点P到原点O的距离OP的长度为 .
10.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=6,AD=3,那么BD= .
11.如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=20,AH=12,那么FG= .
12.已知点A(3,3),B(0,t),C(7,0),且AB=AC,则t= .
13.Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D在AB边上,若△ACD为以AC为腰的等腰三角形,则DC的长为 .
14.如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度由A向B运动,设运动时间为t秒(t>0).在运动过程中,当t为 时,△BCP为等腰三角形.
三.解答题
15.如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,AB=5,AD=2.
(1)求CD的长;
(2)求四边形ABCD的面积.
16.如图,已知△ABC中,∠ACB=90°,过点B作BD∥AC,交∠ACB的平分线CD于点D,CD交BC于点E.
(1)求证:BC=BD;
(2)若AC=3,AB=6,求CD的长.
17.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
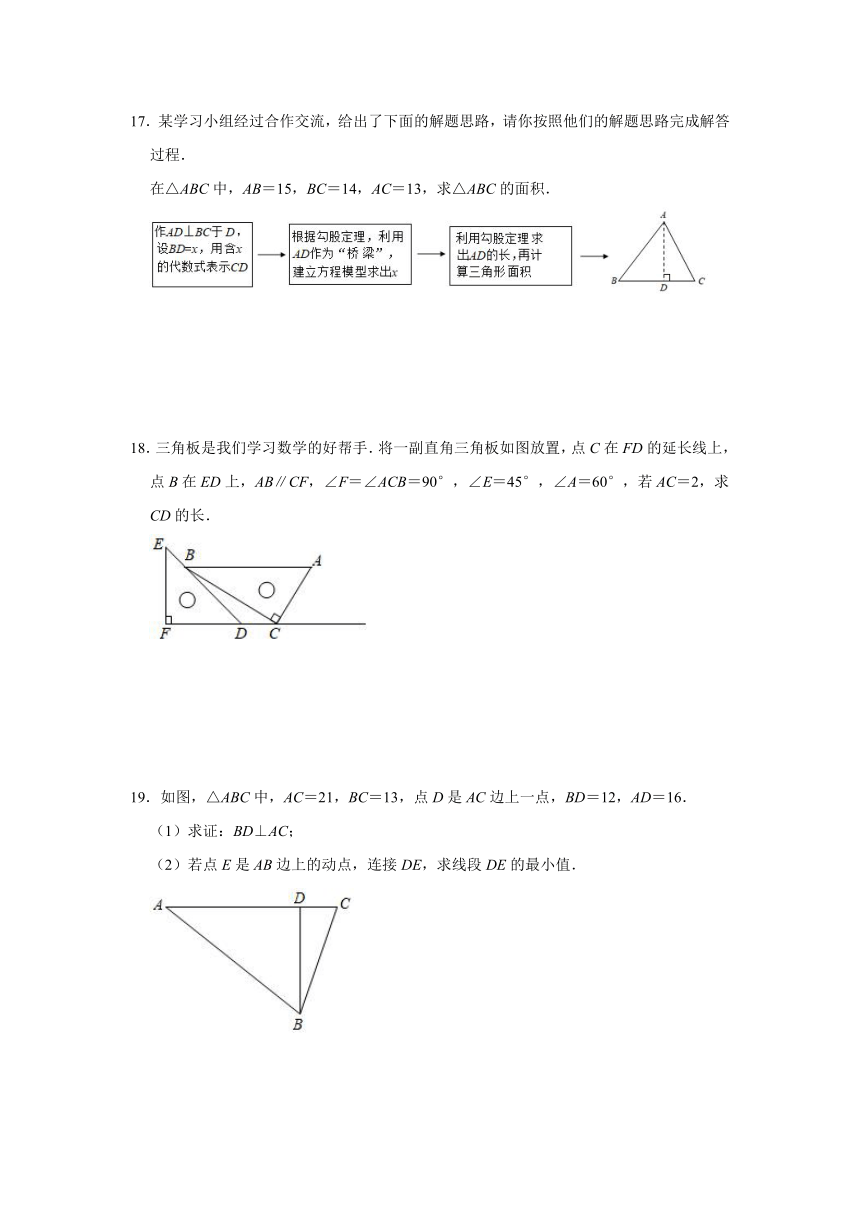
18.三角板是我们学习数学的好帮手.将一副直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,若AC=2,求CD的长.
19.如图,△ABC中,AC=21,BC=13,点D是AC边上一点,BD=12,AD=16.
(1)求证:BD⊥AC;
(2)若点E是AB边上的动点,连接DE,求线段DE的最小值.
20.如图,△ABC中,∠C=90°,CA=8cm,CB=6cm,D为动点,沿着C→A→B→C的路径运动(再次到达C点则停止运动),点D的运动速度为2cm/秒,设点D运动时间为t秒.
(1)当点D在AC上运动时,若DC=BC,则t= ;
(2)若点D与△ABC某一顶点的连线平分△ABC的周长,求t的值.
答案
一.选择题
1.解:由题意可得:BD=4,BC=1
则CD==,
A点对应的实数为:﹣1,
选:C.
2.解:在Rt△ABC中,AC2+AB2=BC2,
由正方形面积公式得S1=AB2,S2=AC2,S3=BC2,
∵S1=9,S2=16,
∴S3=S1+S2=9+16=25.
选:D.
3.解:∵==,可能是“格点线”的长度,选项A不符合题意;
∵==,可能是“格点线”的长度,选项B不符合题意;
∵=3,可能是“格点线”的长度,选项C不符合题意;
∵=,不可能是“格点线”的长度,选项D符合题意;
选:D.
4.解:∵PM⊥OB于点M,OM=4,OP=5,
∴PM=3,
当PN⊥OA时,PN的值最小,
∵OC平分∠AOB,PM⊥OB,
∴PM=PN,
∵PM=3,
∴PN的最小值为3.
选:B.
5.解:∵∠C=90°,
∴a2+b2=c2=144,
∴(a+b)2﹣2ab=144,
∴196﹣2ab=144,
∴ab=26,
∴S△ABC=ab=13cm2.
选:A.
6.解:分两种情况:
①当3和4为两条直角边长时,
由勾股定理得:第三边长的平方=斜边长的平方=32+42=25;
②当4为斜边长时,
第三边长的平方=42﹣32=7;
综上所述:第三边长的平方是7或25.
选:D.
7.解:由勾股定理可知甲、乙、丙三个直角三角形中,斜边的平方分别为:
甲:(2018+2019)2+20202;
乙:(2018+2020)2+20192;
丙:(2019+2020)2+20182.
∵(2018+2019)2+20202﹣[(2018+2020)2+20192]
=40372+20202﹣40382﹣20192
=(40372﹣40382)+(20202﹣20192)
=(4037+4038)(4037﹣4038)+(2020+2019)(2020﹣2019)
=﹣8075+4039
=﹣4036<0,
∴甲的斜边的小于乙的斜边;
∵(2018+2020)2+20192﹣[(2019+2020)2+20182]
=40382+20192﹣40392﹣20182
=(40382﹣40392)+(20192﹣20182)
=(4038+4039)(4038﹣4039)+(2019+2018)(2019﹣2018)
=﹣8077+4037
=﹣4040
<0,
∴乙的斜边的小于丙的斜边,
∴斜边最长的是丙.
选:C.
8.解:设斜边为c,根据勾股定理得出c=,
∵ab=ch,
∴ab=?h,即a2b2=a2h2+b2h2,
∴=+,
即.
选:B.
二.填空题
9.解:∵点P的坐标为(1,﹣3),点O为坐标原点,
∴OP==.
答:点P到原点O的距离OP的长度为.
答案为:.
10.解:在Rt△ACD中,CD===3,
在Rt△BCD中,BC==,
在Rt△ABC中,BC==,
∴=,
解得,BD=9,
答案为:9.
11.解:∵△ABH≌△BCG,
∴BG=AH=12,
∵四边形EFGH都是正方形,
在直角三角形AHB中,由勾股定理得到:BH=.
∴FG=GH=BH﹣BG=16﹣12=4,
答案为:4.
12.解:依题意,得=.
解得t=7或t=﹣1.
答案是:7或﹣1.
13.解:①当AC=CD时,
∵AC=6,
∴CD=6时,△ACD是以AC为腰的等腰三角形;
②当AC=AD′时,过点C作CE⊥AB于点E,
∵∠ACB=90°,AC=6,BC=8,
∴AB===10,
∵?AC?BC=?AB?CE,
∴EC=
∴AE===,
∴ED′=AD′﹣AE=6﹣=,
∴CD′===,
综上所述,CD的长为6或.
答案为:6或.
14.解:当P在AB上时,△BCP为等腰三角形,可分三种情况:
①CP=PB,点P在BC的垂直平分线上,如图1,
∵PC=PB,
∴∠B=∠PCB,
∵∠ACB=90°,
∴∠PCB+∠ACP=90°,∠B+∠A=90°,
∴∠A=∠ACP,
∴AP=PC,
∴PB=AB,即5﹣2t=,
解得:t=,
②PB=BC,
即5﹣2t=3,
解得:t=1,
③PC=BC,
如图3,过点C作CD⊥AB于点D,
∵∠ACB=90°,AB=5cm,BC=3cm,
∴AC===4(cm).
∵S△ABC=×AB×CD,
∴CD==,
∴BD==,
∵PC=BC,CD⊥AB,
∴BD=BP,
∴=×(5﹣2t),
解得:t=,
∴当t=1或或时,△BCP为等腰三角形.
答案为:1或或.
三.解答题
15.解:(1)延长BA、CD交于点H,如图所示:
∵∠B=∠ADC=90°,∠C=60°,
∴∠ADH=90°,∠H=30°,
∴HA=2AD=4,CH=2BC,
∴DH===2,BH=HA+AB=4+5=9,
∵BH===BC=9,
∴BC=3,
∴CH=2BC=6,
∴CD=CH﹣HD=6﹣2=4;
(2)四边形ABCD的面积=△BCH的面积﹣△ADH的面积=×3×9﹣×2×2=.
16.(1)证明:∵∠ACB=90°,CD平分∠ACB,
∴∠BCD=∠ACD=∠ACB=×90°=45°,
∵BD∥AC,
∴∠D=∠ACD=45°,
∴∠D=∠BCD,
∴BC=BD;
(2)解:在Rt△ACB中,BC===3,
∴BD=3,
∵∠BCD=∠D=45°,
∴∠CBD=90°,
∴CD===3.
17.解:在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则CD=14﹣x,
由勾股定理得:AD2=AB2﹣BD2=152﹣x2,AD2=AC2﹣CD2=132﹣(14﹣x)2,
∴152﹣x2=132﹣(14﹣x)2,
解得:x=9,
∴AD=12,
∴S△ABC=BC?AD=×14×12=84.
18.解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=2,
∴∠ABC=30°,
∴AB=2AC=4.
∴BC===2,
∵AB∥CF,
∴∠BCM=∠ABC=30°,
∴BM=BC=,
∴CM==3,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=,
∴CD=CM﹣MD=3﹣.
19.解:(1)∵AC=21,AD=16,
∴CD=AC﹣AD=5,
∵BD2+CD2=122+52=169=BC2,
∴∠BDC=90°,
∴BD⊥AC.
(2)当DE⊥AB时,DE最短,
∵AB==20,
∵?AD?DB=?AB?DE,
∴DE==9.6,
∴线段DE使得最小值为9.6.
20.解:(1)∵DC=BC=6,
∴2t=6,
解得:t==3,
当点D在AC上运动时,若DC=BC,则t=3;
答案为:3;
(2)△ABC中,∠C=90°,CA=8,CB=6,
∴AB==10,
∴△ABC的周长=6+8+10=24,
①当点D在CA上运动时,如图1,BC+CD=AB+AD,
即6+2t=,
解得:t=3;
②当点D在AB上运动时,如图2,AC+AD=BD+BC,
即2t=,
解得:t=6;
③当点D在BC上运动时,如图3,AB+BD=CD+AC,
即2t﹣8=,
解得:t=10;
综上所述,t的值是3或6或10.
一.选择题
1.如图所示,点B,D在数轴上,OB=3,OD=BC=1,∠OBC=90°,以D为圆心,DC长为半径画弧,与数轴正半轴交于点A,则点A表示的实数是( )
A. B.+1 C.﹣1 D.不能确定
2.如图,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3.若S1=9,S2=16,则S3的值为( )
A.7 B.10 C.20 D.25
3.如图,在行距、列距都是1的的4×4方格网中,将任意连接两个格点的线段称作“格点线”,则“格点线”的长度不可能等于( )
A. B. C. D.
4.如图,OC平分∠AOB,点P是OC上一点,PM⊥OB于点M,点N是射线OA上的一个动点若OM=4,OP=5,则PN的最小值为( )
A.2 B.3 C.4 D.5
5.已知Rt△ABC中,∠C=90°.若a+b=14cm,c=12cm,则Rt△ABC的面积是( )
A.13cm2 B.26cm2 C.48cm2 D.52cm2
6.直角三角形中,有两边的长分别为3和4,那么第三边的长的平方为( )
A.25 B.14 C.7 D.7或25
7.如图,甲、乙、丙三个直角三角形中,斜边最长的是( )
A.甲 B.乙 C.丙 D.一样长
8.在直角三角形ABC中,∠C=90°,两直角边长及斜边上的高分别为a,b,h,则下列关系式成立的是( )
A. B.
C.h2=ab D.h2=a2+b2
二.填空题
9.在平面直角坐标系中,已知点P的坐标为(1,﹣3),那么点P到原点O的距离OP的长度为 .
10.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=6,AD=3,那么BD= .
11.如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=20,AH=12,那么FG= .
12.已知点A(3,3),B(0,t),C(7,0),且AB=AC,则t= .
13.Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D在AB边上,若△ACD为以AC为腰的等腰三角形,则DC的长为 .
14.如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度由A向B运动,设运动时间为t秒(t>0).在运动过程中,当t为 时,△BCP为等腰三角形.
三.解答题
15.如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,AB=5,AD=2.
(1)求CD的长;
(2)求四边形ABCD的面积.
16.如图,已知△ABC中,∠ACB=90°,过点B作BD∥AC,交∠ACB的平分线CD于点D,CD交BC于点E.
(1)求证:BC=BD;
(2)若AC=3,AB=6,求CD的长.
17.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
18.三角板是我们学习数学的好帮手.将一副直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,若AC=2,求CD的长.
19.如图,△ABC中,AC=21,BC=13,点D是AC边上一点,BD=12,AD=16.
(1)求证:BD⊥AC;
(2)若点E是AB边上的动点,连接DE,求线段DE的最小值.
20.如图,△ABC中,∠C=90°,CA=8cm,CB=6cm,D为动点,沿着C→A→B→C的路径运动(再次到达C点则停止运动),点D的运动速度为2cm/秒,设点D运动时间为t秒.
(1)当点D在AC上运动时,若DC=BC,则t= ;
(2)若点D与△ABC某一顶点的连线平分△ABC的周长,求t的值.
答案
一.选择题
1.解:由题意可得:BD=4,BC=1
则CD==,
A点对应的实数为:﹣1,
选:C.
2.解:在Rt△ABC中,AC2+AB2=BC2,
由正方形面积公式得S1=AB2,S2=AC2,S3=BC2,
∵S1=9,S2=16,
∴S3=S1+S2=9+16=25.
选:D.
3.解:∵==,可能是“格点线”的长度,选项A不符合题意;
∵==,可能是“格点线”的长度,选项B不符合题意;
∵=3,可能是“格点线”的长度,选项C不符合题意;
∵=,不可能是“格点线”的长度,选项D符合题意;
选:D.
4.解:∵PM⊥OB于点M,OM=4,OP=5,
∴PM=3,
当PN⊥OA时,PN的值最小,
∵OC平分∠AOB,PM⊥OB,
∴PM=PN,
∵PM=3,
∴PN的最小值为3.
选:B.
5.解:∵∠C=90°,
∴a2+b2=c2=144,
∴(a+b)2﹣2ab=144,
∴196﹣2ab=144,
∴ab=26,
∴S△ABC=ab=13cm2.
选:A.
6.解:分两种情况:
①当3和4为两条直角边长时,
由勾股定理得:第三边长的平方=斜边长的平方=32+42=25;
②当4为斜边长时,
第三边长的平方=42﹣32=7;
综上所述:第三边长的平方是7或25.
选:D.
7.解:由勾股定理可知甲、乙、丙三个直角三角形中,斜边的平方分别为:
甲:(2018+2019)2+20202;
乙:(2018+2020)2+20192;
丙:(2019+2020)2+20182.
∵(2018+2019)2+20202﹣[(2018+2020)2+20192]
=40372+20202﹣40382﹣20192
=(40372﹣40382)+(20202﹣20192)
=(4037+4038)(4037﹣4038)+(2020+2019)(2020﹣2019)
=﹣8075+4039
=﹣4036<0,
∴甲的斜边的小于乙的斜边;
∵(2018+2020)2+20192﹣[(2019+2020)2+20182]
=40382+20192﹣40392﹣20182
=(40382﹣40392)+(20192﹣20182)
=(4038+4039)(4038﹣4039)+(2019+2018)(2019﹣2018)
=﹣8077+4037
=﹣4040
<0,
∴乙的斜边的小于丙的斜边,
∴斜边最长的是丙.
选:C.
8.解:设斜边为c,根据勾股定理得出c=,
∵ab=ch,
∴ab=?h,即a2b2=a2h2+b2h2,
∴=+,
即.
选:B.
二.填空题
9.解:∵点P的坐标为(1,﹣3),点O为坐标原点,
∴OP==.
答:点P到原点O的距离OP的长度为.
答案为:.
10.解:在Rt△ACD中,CD===3,
在Rt△BCD中,BC==,
在Rt△ABC中,BC==,
∴=,
解得,BD=9,
答案为:9.
11.解:∵△ABH≌△BCG,
∴BG=AH=12,
∵四边形EFGH都是正方形,
在直角三角形AHB中,由勾股定理得到:BH=.
∴FG=GH=BH﹣BG=16﹣12=4,
答案为:4.
12.解:依题意,得=.
解得t=7或t=﹣1.
答案是:7或﹣1.
13.解:①当AC=CD时,
∵AC=6,
∴CD=6时,△ACD是以AC为腰的等腰三角形;
②当AC=AD′时,过点C作CE⊥AB于点E,
∵∠ACB=90°,AC=6,BC=8,
∴AB===10,
∵?AC?BC=?AB?CE,
∴EC=
∴AE===,
∴ED′=AD′﹣AE=6﹣=,
∴CD′===,
综上所述,CD的长为6或.
答案为:6或.
14.解:当P在AB上时,△BCP为等腰三角形,可分三种情况:
①CP=PB,点P在BC的垂直平分线上,如图1,
∵PC=PB,
∴∠B=∠PCB,
∵∠ACB=90°,
∴∠PCB+∠ACP=90°,∠B+∠A=90°,
∴∠A=∠ACP,
∴AP=PC,
∴PB=AB,即5﹣2t=,
解得:t=,
②PB=BC,
即5﹣2t=3,
解得:t=1,
③PC=BC,
如图3,过点C作CD⊥AB于点D,
∵∠ACB=90°,AB=5cm,BC=3cm,
∴AC===4(cm).
∵S△ABC=×AB×CD,
∴CD==,
∴BD==,
∵PC=BC,CD⊥AB,
∴BD=BP,
∴=×(5﹣2t),
解得:t=,
∴当t=1或或时,△BCP为等腰三角形.
答案为:1或或.
三.解答题
15.解:(1)延长BA、CD交于点H,如图所示:
∵∠B=∠ADC=90°,∠C=60°,
∴∠ADH=90°,∠H=30°,
∴HA=2AD=4,CH=2BC,
∴DH===2,BH=HA+AB=4+5=9,
∵BH===BC=9,
∴BC=3,
∴CH=2BC=6,
∴CD=CH﹣HD=6﹣2=4;
(2)四边形ABCD的面积=△BCH的面积﹣△ADH的面积=×3×9﹣×2×2=.
16.(1)证明:∵∠ACB=90°,CD平分∠ACB,
∴∠BCD=∠ACD=∠ACB=×90°=45°,
∵BD∥AC,
∴∠D=∠ACD=45°,
∴∠D=∠BCD,
∴BC=BD;
(2)解:在Rt△ACB中,BC===3,
∴BD=3,
∵∠BCD=∠D=45°,
∴∠CBD=90°,
∴CD===3.
17.解:在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则CD=14﹣x,
由勾股定理得:AD2=AB2﹣BD2=152﹣x2,AD2=AC2﹣CD2=132﹣(14﹣x)2,
∴152﹣x2=132﹣(14﹣x)2,
解得:x=9,
∴AD=12,
∴S△ABC=BC?AD=×14×12=84.
18.解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=2,
∴∠ABC=30°,
∴AB=2AC=4.
∴BC===2,
∵AB∥CF,
∴∠BCM=∠ABC=30°,
∴BM=BC=,
∴CM==3,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=,
∴CD=CM﹣MD=3﹣.
19.解:(1)∵AC=21,AD=16,
∴CD=AC﹣AD=5,
∵BD2+CD2=122+52=169=BC2,
∴∠BDC=90°,
∴BD⊥AC.
(2)当DE⊥AB时,DE最短,
∵AB==20,
∵?AD?DB=?AB?DE,
∴DE==9.6,
∴线段DE使得最小值为9.6.
20.解:(1)∵DC=BC=6,
∴2t=6,
解得:t==3,
当点D在AC上运动时,若DC=BC,则t=3;
答案为:3;
(2)△ABC中,∠C=90°,CA=8,CB=6,
∴AB==10,
∴△ABC的周长=6+8+10=24,
①当点D在CA上运动时,如图1,BC+CD=AB+AD,
即6+2t=,
解得:t=3;
②当点D在AB上运动时,如图2,AC+AD=BD+BC,
即2t=,
解得:t=6;
③当点D在BC上运动时,如图3,AB+BD=CD+AC,
即2t﹣8=,
解得:t=10;
综上所述,t的值是3或6或10.
