4.1认识三角形课时训练(Word版 含答案)
文档属性
| 名称 | 4.1认识三角形课时训练(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 362.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 10:15:59 | ||
图片预览

文档简介
4.1认识三角形课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,平分,,则( )
A. B. C. D.
2.在三角形中,一定能将其面积分成相等两部分的是( )
A.中线 B.高线 C.角平分线 D.某一边的垂直平分线
3.三角形的内角和等于( )
A. B. C. D.
4.如图,在△ABC中,已知点 D,E,F 分别是 BC,AD,CE 的中点,且SΔABC=8,则SΔBEF的值是( )
A.2 B.3 C.4 D.5
5.如图,在中,,,为中线,则与的周长之差为( )
A.1 B.2 C.3 D.4
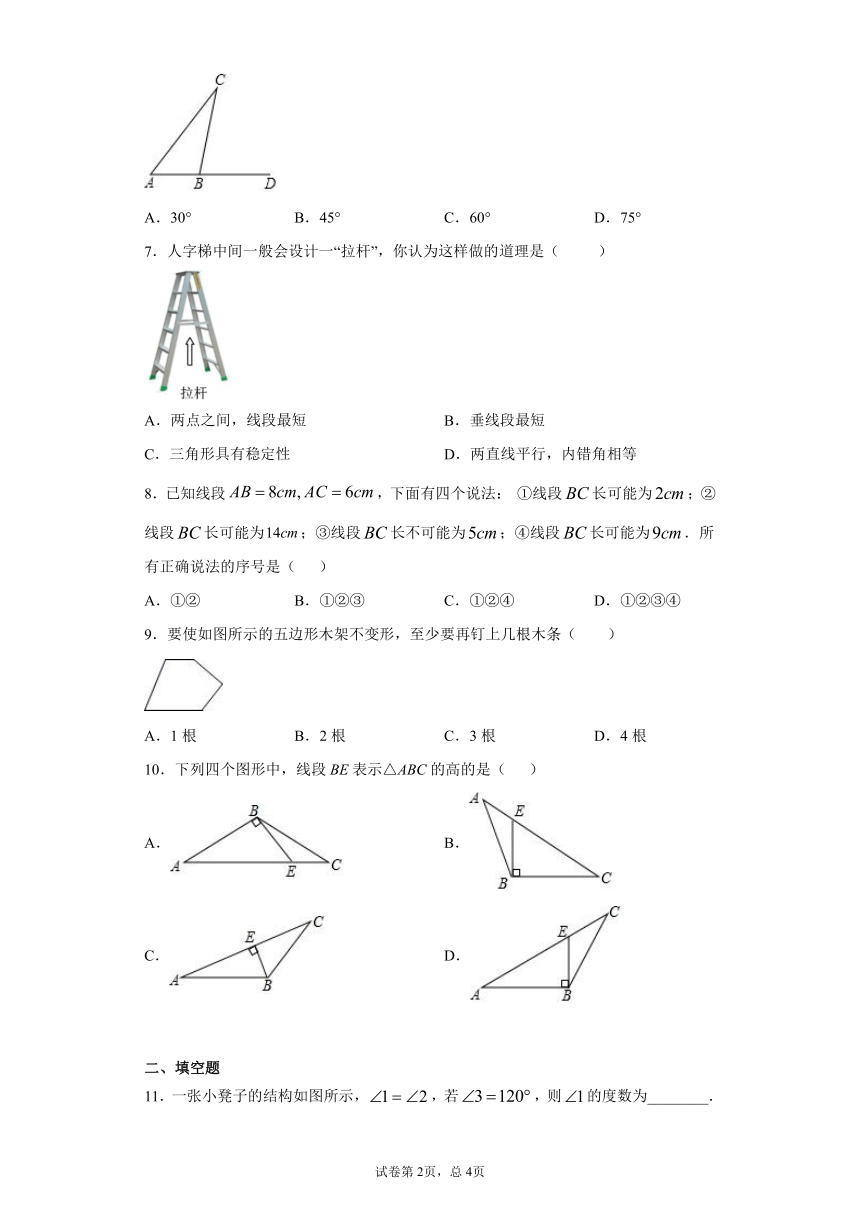
6.如图,在中,,的外角,则的度数是( )
A.30° B.45° C.60° D.75°
7.人字梯中间一般会设计一“拉杆”,你认为这样做的道理是( )
A.两点之间,线段最短 B.垂线段最短
C.三角形具有稳定性 D.两直线平行,内错角相等
8.已知线段,下面有四个说法: ①线段长可能为;②线段长可能为;③线段长不可能为;④线段长可能为.所有正确说法的序号是( )
A.①② B.①②③ C.①②④ D.①②③④
9.要使如图所示的五边形木架不变形,至少要再钉上几根木条( )
A.1根 B.2根 C.3根 D.4根
10.下列四个图形中,线段BE表示△ABC的高的是( )
A. B.
C. D.
二、填空题
11.一张小凳子的结构如图所示,,若,则的度数为________.
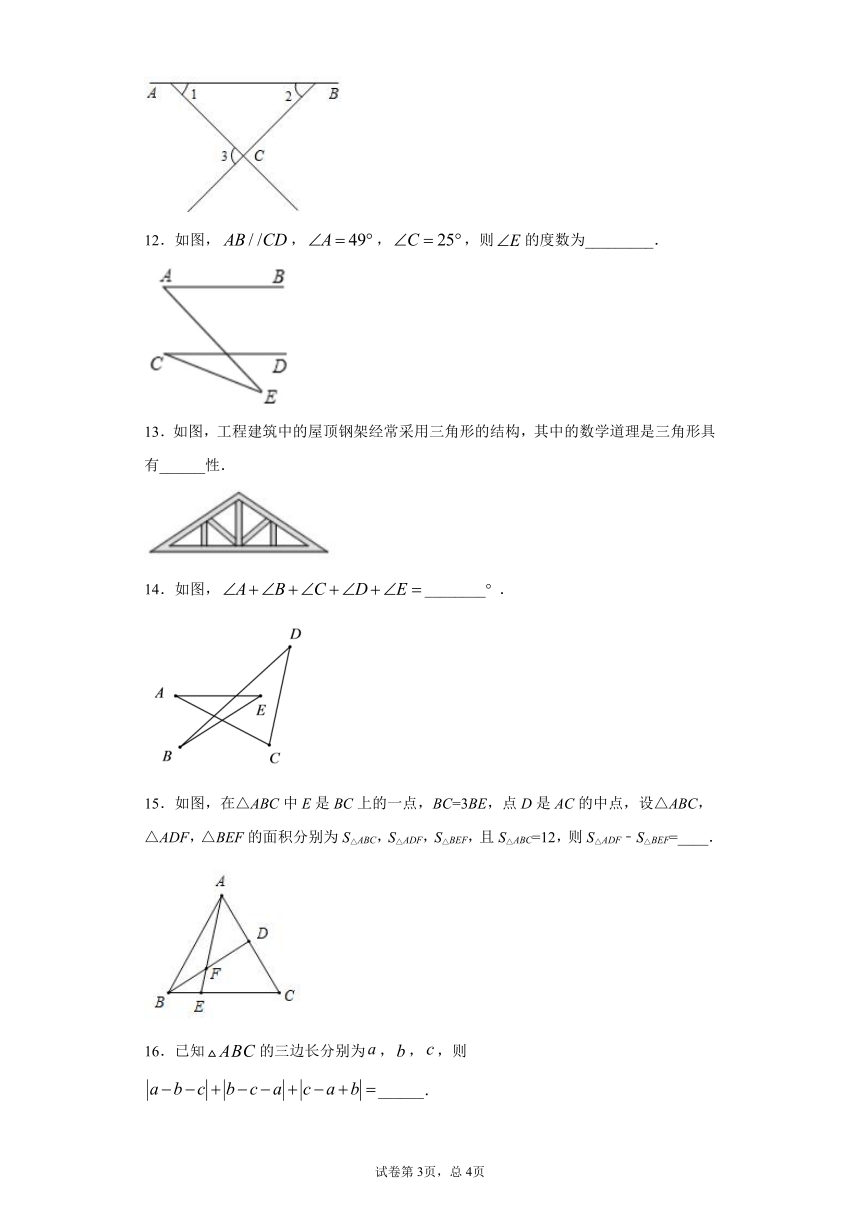
12.如图,,,,则的度数为_________.
13.如图,工程建筑中的屋顶钢架经常采用三角形的结构,其中的数学道理是三角形具有______性.
14.如图,________° .
15.如图,在△ABC中E是BC上的一点,BC=3BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF﹣S△BEF=____.
16.已知的三边长分别为,,,则______.
三、解答题
17.(1)已知直线,小亮把一块含角的直角三角尺的直角顶点放在直线上.
①若三角尺与平行线的位置如图1所示,,求的度数;
②若三角尺与平行线的位置如图2所示,且,则的度数又是多少?
(2)已知直线,小亮把一块含角的直角三角尺按图3所示放置,若,求的度数.
18.已知,的三边长为,,.
(1)求的周长的取值范围;
(2)当的周长为偶数时,求.
19.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为120°,40°,20°的三角形是“三倍角三角形”.
(1)△ABC中,∠A=35°,∠B=40°,△ABC是“三倍角三角形”吗?为什么?
(2)若△ABC是“三倍角三角形”,且∠B=60°,求△ABC中最小内角的度数.
20.如图,在平面内有三个点
(1)根据下列语句画图:
①连接;
②作直线;
③作射线,在的延长线上取一点使得,连接;
(2)比较的大小关系.
参考答案
1.D
2.A
3.C
4.A
5.B
6.A
7.C
8.C
9.B
10.C
11.60°
12.24°
13.稳定
14.180
15.2
16.
17.(1)①50°;②20°;(2)35°
【详解】
解:(1)①如图①∵∠1=40°,
∴∠3=180°-∠1-90°=180°-40°-90°=50°,
∵a∥b,
∴∠2=∠3=50°;
②如图②过点B作BD∥a,
∵直线a∥b,
∴BD∥a∥b,
∴∠4=∠1=25°,
∵∠ABC=45°,
∴∠3=∠ABC-∠4=45°-25°=20°,
∴∠2=∠3=20°;
(2)如图3,∵∠3是△ADG的外角,
∴∠3=∠A+∠1=30°+25°=55°,
∵直线a∥b,
∴∠3=∠4=55°,
∵∠4+∠EFC=90°,
∴∠EFC=90°-55°=35°,
∴∠2=35°.
18.(1)的周长;(2),或.
【详解】
解:(1)的三边长分别为,,,
,即,
的周长,
即:的周长;
(2)的周长是偶数,由(1)结果得的周长可以是,或,
的值为,或.
19.(1)是,理由见解析;(2)20°或30°
【详解】
解:(1) ∠A=35°,∠B=40°,
△ABC是“三倍角三角形”.
(2) △ABC是“三倍角三角形”,且∠B=60°,不妨设
当时,则
当时,
当时,则 不合题意舍去,
综上:△ABC是“三倍角三角形”,△ABC中最小内角的度数为或
20.(1)见解析;(2)
【详解】
解:(1)①如图,线段AB即为所求;
②如图,直线BC即为所求;
③如图,射线AC,点D,线段BD即为所求
(2)如图,在△BCD中,BC+CD>BD
∴
在△ABD中,AB+BD>AD
∴
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,平分,,则( )
A. B. C. D.
2.在三角形中,一定能将其面积分成相等两部分的是( )
A.中线 B.高线 C.角平分线 D.某一边的垂直平分线
3.三角形的内角和等于( )
A. B. C. D.
4.如图,在△ABC中,已知点 D,E,F 分别是 BC,AD,CE 的中点,且SΔABC=8,则SΔBEF的值是( )
A.2 B.3 C.4 D.5
5.如图,在中,,,为中线,则与的周长之差为( )
A.1 B.2 C.3 D.4
6.如图,在中,,的外角,则的度数是( )
A.30° B.45° C.60° D.75°
7.人字梯中间一般会设计一“拉杆”,你认为这样做的道理是( )
A.两点之间,线段最短 B.垂线段最短
C.三角形具有稳定性 D.两直线平行,内错角相等
8.已知线段,下面有四个说法: ①线段长可能为;②线段长可能为;③线段长不可能为;④线段长可能为.所有正确说法的序号是( )
A.①② B.①②③ C.①②④ D.①②③④
9.要使如图所示的五边形木架不变形,至少要再钉上几根木条( )
A.1根 B.2根 C.3根 D.4根
10.下列四个图形中,线段BE表示△ABC的高的是( )
A. B.
C. D.
二、填空题
11.一张小凳子的结构如图所示,,若,则的度数为________.
12.如图,,,,则的度数为_________.
13.如图,工程建筑中的屋顶钢架经常采用三角形的结构,其中的数学道理是三角形具有______性.
14.如图,________° .
15.如图,在△ABC中E是BC上的一点,BC=3BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF﹣S△BEF=____.
16.已知的三边长分别为,,,则______.
三、解答题
17.(1)已知直线,小亮把一块含角的直角三角尺的直角顶点放在直线上.
①若三角尺与平行线的位置如图1所示,,求的度数;
②若三角尺与平行线的位置如图2所示,且,则的度数又是多少?
(2)已知直线,小亮把一块含角的直角三角尺按图3所示放置,若,求的度数.
18.已知,的三边长为,,.
(1)求的周长的取值范围;
(2)当的周长为偶数时,求.
19.在一个三角形中,如果一个内角是另一个内角的3倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为120°,40°,20°的三角形是“三倍角三角形”.
(1)△ABC中,∠A=35°,∠B=40°,△ABC是“三倍角三角形”吗?为什么?
(2)若△ABC是“三倍角三角形”,且∠B=60°,求△ABC中最小内角的度数.
20.如图,在平面内有三个点
(1)根据下列语句画图:
①连接;
②作直线;
③作射线,在的延长线上取一点使得,连接;
(2)比较的大小关系.
参考答案
1.D
2.A
3.C
4.A
5.B
6.A
7.C
8.C
9.B
10.C
11.60°
12.24°
13.稳定
14.180
15.2
16.
17.(1)①50°;②20°;(2)35°
【详解】
解:(1)①如图①∵∠1=40°,
∴∠3=180°-∠1-90°=180°-40°-90°=50°,
∵a∥b,
∴∠2=∠3=50°;
②如图②过点B作BD∥a,
∵直线a∥b,
∴BD∥a∥b,
∴∠4=∠1=25°,
∵∠ABC=45°,
∴∠3=∠ABC-∠4=45°-25°=20°,
∴∠2=∠3=20°;
(2)如图3,∵∠3是△ADG的外角,
∴∠3=∠A+∠1=30°+25°=55°,
∵直线a∥b,
∴∠3=∠4=55°,
∵∠4+∠EFC=90°,
∴∠EFC=90°-55°=35°,
∴∠2=35°.
18.(1)的周长;(2),或.
【详解】
解:(1)的三边长分别为,,,
,即,
的周长,
即:的周长;
(2)的周长是偶数,由(1)结果得的周长可以是,或,
的值为,或.
19.(1)是,理由见解析;(2)20°或30°
【详解】
解:(1) ∠A=35°,∠B=40°,
△ABC是“三倍角三角形”.
(2) △ABC是“三倍角三角形”,且∠B=60°,不妨设
当时,则
当时,
当时,则 不合题意舍去,
综上:△ABC是“三倍角三角形”,△ABC中最小内角的度数为或
20.(1)见解析;(2)
【详解】
解:(1)①如图,线段AB即为所求;
②如图,直线BC即为所求;
③如图,射线AC,点D,线段BD即为所求
(2)如图,在△BCD中,BC+CD>BD
∴
在△ABD中,AB+BD>AD
∴
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
