2020-2021学年高中数学苏教版必修2单元测试卷 第一章 立体几何初步 Word版含解析
文档属性
| 名称 | 2020-2021学年高中数学苏教版必修2单元测试卷 第一章 立体几何初步 Word版含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 652.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览



文档简介
第一章 立体几何初步
1.在边长为30米的正六边形广场正上空悬挂一个照明光源,已知这个光源发出的光线过旋转轴的截面是一个等腰直角三角形,要使整个广场都照明,光源悬挂的高度至少为( )
A.30米 B.20米 C.米 D.15米
2.如图,圆柱的底面半径为1,平面为圆柱的轴截面,从点开始,沿着圆柱的侧面拉一条绳子到点,若绳子的最短长度为,则该圆柱的侧面积为( )
A. B. C. D.
3.《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(网格纸上小正方形的边长为1),则该“阳马”最长的棱长为(?? )
A.5 B. C. D.
4.如图,梯形是一平面图形ABCD的直观图(斜二测),若,,,,则梯形的面积是( )
A.10 B.5 C. D.
5.在三棱锥的棱上分别取四点,如果,则点( )
A.一定在直线上 B.一定在直线上
C.在直线或上 D.不在直线上,也不在直线上
6.若为异面直线,直线,则与的位置关系是( )
A.相交 B.异面 C.平行 ?D. 异面或相交
7.已知的一个内角为,并且三边长构成公差为2的等差数列,则的周长为( )
A.15 B.18 C.21 D.24
8.三棱锥中,平面与平面的法向量分别为.若,则二面角的大小为( )
A. B. C.或 D.或
9.已知圆柱的上、下底面的中心分别为,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A. B. C. D.
10.《九章算术》是我国古代第一部数学专著,它有如下问题:“今有圆堡瑽(cōng),周四丈八尺,高一丈一尺。问积几何?”意思是“今有圆柱体形的土筑小城堡,底面周长为4丈8尺,高1丈1尺。问它的体积是( )?”(注:1丈=10尺,取)
A.704立方尺 B.2112立方尺 C.2115立方尺 D.2118立方尺
11.已知圆锥的顶点为,母线所成角的余弦值为.与圆锥底面所成角为45°.若的面积为,则该圆锥的侧面积为______________.
12.某空间几何体的三视图如图所示,且该几何体的体积为1,则该几何体的所有面中最大面的面积为____________.
13.三棱柱中,平面平面,,是等腰直角三角形,,,则异面直线与所成角的余弦值为_______.
14.若圆锥的母线长为4,底面半径为,则圆锥的体积为______.
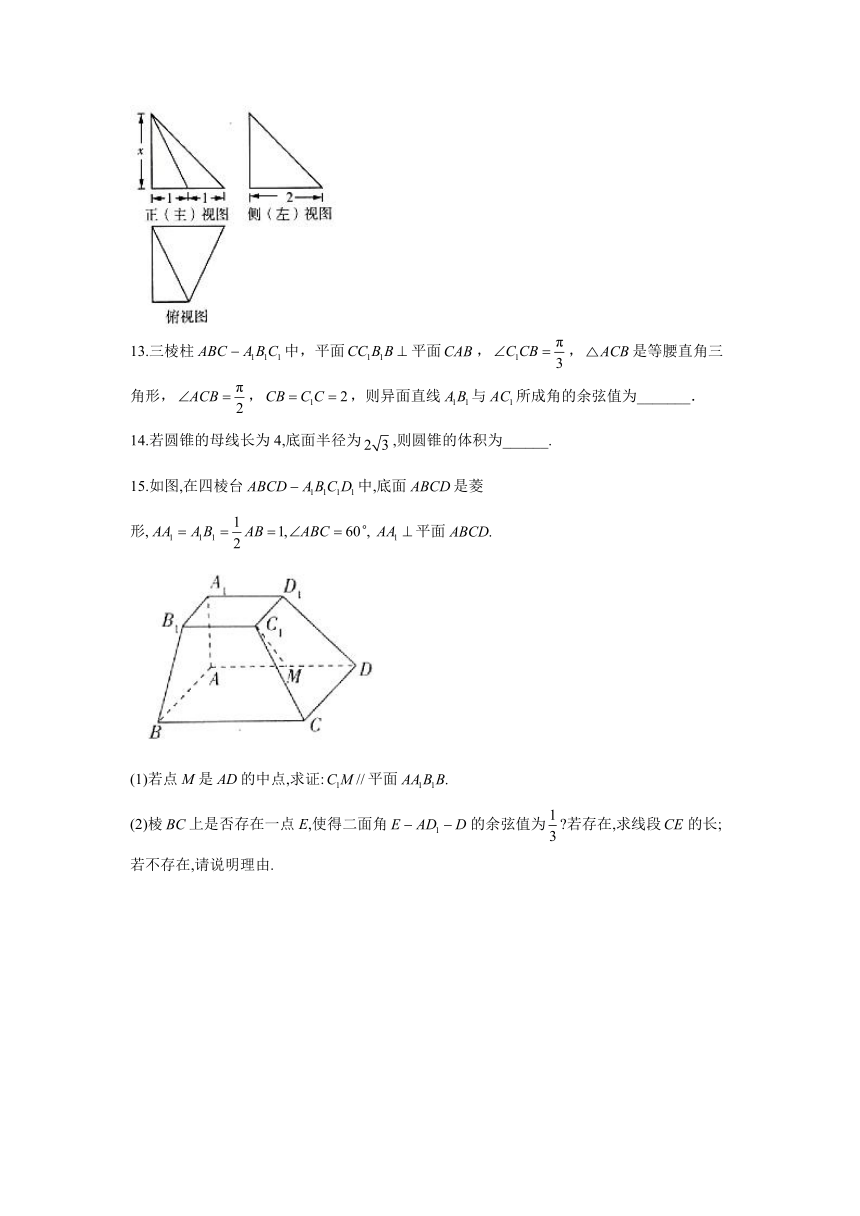
15.如图,在四棱台中,底面是菱形,平面
(1)若点M是的中点,求证:平面
(2)棱上是否存在一点E,使得二面角的余弦值为?若存在,求线段的长;若不存在,请说明理由.
答案以及解析
1.答案:A
解析:设正六边形广场为,光源悬挂的最低点为,则正六棱锥的底面边长为30米,高即所求,由题意可知为等腰直角三角形,米,所以正六棱锥的高为斜边的一半,即30米,故选A.
2.答案:A
解析:沿将圆柱的侧面展开,绳子的最短长度即侧面展开图中两点间的距离,连接,则,展开后的长度为.设圆柱的高为,则,即,得,所以圆柱的侧面积为.
3.答案:D
解析:由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,如图:
其中 平面,∴,,,∴,,.该几何体最长棱的棱长为.故选D.
4.答案:B
解析:如图,根据直观图画法的规则,直观图中,,原图中,从而得出,且,直观图中,, 原图中,,即四边形ABCD上底和下底边长分别为2,3,高为2,如图.故其面积.所以B选项是正确的.
5.答案:B
解析:如图所示,∵ 平面ABC,平面ACD,,∴平面ABC,平面ACD.又∵平面平面,,故选B.
6.答案:D
解析:若,这与是异面直线相矛盾;所以异面或相交
故选D
7.答案:A
解析:设中项为a则最短边为, 最长边为
则根据余弦定理
即
所以,或者(舍)
所以三角形的周长为
8.答案:C
解析:当二面角的大小为锐角时,其大小为;当二面角的大小为钝角时,其大小为.
9.答案:C
解析:设圆柱的底面半径为,高为,由题意得,所以,所以圆柱的表面积为.故选C.
10.答案:B
解析:设圆柱形城堡的底面半径为尺,高为尺,则尺,∴,
∴城堡的体积立方尺。
故选:B.
11.答案:
解析:如图所示,设在底面的射影为,连接.的面积为,.与底面所成的角为45°,底面周长圆锥的侧面积为.
12.答案:3
解析:由三视图可知,该几何体为如图所示的四棱锥,记为,其中平面,由该几何体的体积为1,得,解得,故,易得,
,,,故该几何体中最大面的面积为3 .
13.答案:
解析:因为,,所以,
又因为是等腰直角三角形,,,所以,
因为,又,平面平面
所以平面,所以.又,所以
根据题意可知异面直线与所成角为,
根据余弦定理得,
故答案为.
14.答案:
解析:因为圆锥的母线长为4,底面半径为,
所以圆锥的高为2,
所以圆锥的体积为.
故答案为:
15.答案:(1)证明:连接
由已知得且
所以四边形是平行四边形,所以
又因为平面平面
所以平面
(2)解:取中点Q,连接
因为是菱形,且
所以是正三角形,
所以即
又由于平面,
所以以所在直线分别为x轴、y轴、z轴,
建立空间直角坐标系,如图
则
假设点E存在,设点E的坐标为
所以
设平面的法向量,
则即可取
易知平面的法向量为
所以
解得
又由于二面角为锐角,由图可知,点E在线段上,
所以即
1.在边长为30米的正六边形广场正上空悬挂一个照明光源,已知这个光源发出的光线过旋转轴的截面是一个等腰直角三角形,要使整个广场都照明,光源悬挂的高度至少为( )
A.30米 B.20米 C.米 D.15米
2.如图,圆柱的底面半径为1,平面为圆柱的轴截面,从点开始,沿着圆柱的侧面拉一条绳子到点,若绳子的最短长度为,则该圆柱的侧面积为( )
A. B. C. D.
3.《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(网格纸上小正方形的边长为1),则该“阳马”最长的棱长为(?? )
A.5 B. C. D.
4.如图,梯形是一平面图形ABCD的直观图(斜二测),若,,,,则梯形的面积是( )
A.10 B.5 C. D.
5.在三棱锥的棱上分别取四点,如果,则点( )
A.一定在直线上 B.一定在直线上
C.在直线或上 D.不在直线上,也不在直线上
6.若为异面直线,直线,则与的位置关系是( )
A.相交 B.异面 C.平行 ?D. 异面或相交
7.已知的一个内角为,并且三边长构成公差为2的等差数列,则的周长为( )
A.15 B.18 C.21 D.24
8.三棱锥中,平面与平面的法向量分别为.若,则二面角的大小为( )
A. B. C.或 D.或
9.已知圆柱的上、下底面的中心分别为,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A. B. C. D.
10.《九章算术》是我国古代第一部数学专著,它有如下问题:“今有圆堡瑽(cōng),周四丈八尺,高一丈一尺。问积几何?”意思是“今有圆柱体形的土筑小城堡,底面周长为4丈8尺,高1丈1尺。问它的体积是( )?”(注:1丈=10尺,取)
A.704立方尺 B.2112立方尺 C.2115立方尺 D.2118立方尺
11.已知圆锥的顶点为,母线所成角的余弦值为.与圆锥底面所成角为45°.若的面积为,则该圆锥的侧面积为______________.
12.某空间几何体的三视图如图所示,且该几何体的体积为1,则该几何体的所有面中最大面的面积为____________.
13.三棱柱中,平面平面,,是等腰直角三角形,,,则异面直线与所成角的余弦值为_______.
14.若圆锥的母线长为4,底面半径为,则圆锥的体积为______.
15.如图,在四棱台中,底面是菱形,平面
(1)若点M是的中点,求证:平面
(2)棱上是否存在一点E,使得二面角的余弦值为?若存在,求线段的长;若不存在,请说明理由.
答案以及解析
1.答案:A
解析:设正六边形广场为,光源悬挂的最低点为,则正六棱锥的底面边长为30米,高即所求,由题意可知为等腰直角三角形,米,所以正六棱锥的高为斜边的一半,即30米,故选A.
2.答案:A
解析:沿将圆柱的侧面展开,绳子的最短长度即侧面展开图中两点间的距离,连接,则,展开后的长度为.设圆柱的高为,则,即,得,所以圆柱的侧面积为.
3.答案:D
解析:由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,如图:
其中 平面,∴,,,∴,,.该几何体最长棱的棱长为.故选D.
4.答案:B
解析:如图,根据直观图画法的规则,直观图中,,原图中,从而得出,且,直观图中,, 原图中,,即四边形ABCD上底和下底边长分别为2,3,高为2,如图.故其面积.所以B选项是正确的.
5.答案:B
解析:如图所示,∵ 平面ABC,平面ACD,,∴平面ABC,平面ACD.又∵平面平面,,故选B.
6.答案:D
解析:若,这与是异面直线相矛盾;所以异面或相交
故选D
7.答案:A
解析:设中项为a则最短边为, 最长边为
则根据余弦定理
即
所以,或者(舍)
所以三角形的周长为
8.答案:C
解析:当二面角的大小为锐角时,其大小为;当二面角的大小为钝角时,其大小为.
9.答案:C
解析:设圆柱的底面半径为,高为,由题意得,所以,所以圆柱的表面积为.故选C.
10.答案:B
解析:设圆柱形城堡的底面半径为尺,高为尺,则尺,∴,
∴城堡的体积立方尺。
故选:B.
11.答案:
解析:如图所示,设在底面的射影为,连接.的面积为,.与底面所成的角为45°,底面周长圆锥的侧面积为.
12.答案:3
解析:由三视图可知,该几何体为如图所示的四棱锥,记为,其中平面,由该几何体的体积为1,得,解得,故,易得,
,,,故该几何体中最大面的面积为3 .
13.答案:
解析:因为,,所以,
又因为是等腰直角三角形,,,所以,
因为,又,平面平面
所以平面,所以.又,所以
根据题意可知异面直线与所成角为,
根据余弦定理得,
故答案为.
14.答案:
解析:因为圆锥的母线长为4,底面半径为,
所以圆锥的高为2,
所以圆锥的体积为.
故答案为:
15.答案:(1)证明:连接
由已知得且
所以四边形是平行四边形,所以
又因为平面平面
所以平面
(2)解:取中点Q,连接
因为是菱形,且
所以是正三角形,
所以即
又由于平面,
所以以所在直线分别为x轴、y轴、z轴,
建立空间直角坐标系,如图
则
假设点E存在,设点E的坐标为
所以
设平面的法向量,
则即可取
易知平面的法向量为
所以
解得
又由于二面角为锐角,由图可知,点E在线段上,
所以即
