新人教A版高中数学必修第一册:指数函数
文档属性
| 名称 | 新人教A版高中数学必修第一册:指数函数 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 00:00:00 | ||
图片预览





文档简介
授课主题:指数函数
教学目标
1.熟练掌握指数函数的图象和性质.2.会求指数型函数y=kax(k∈R,a>0且a≠1)的定义域、值域,并能判断其单调性.3.理解指数函数的简单应用模型,培养数学应用意识
教学内容
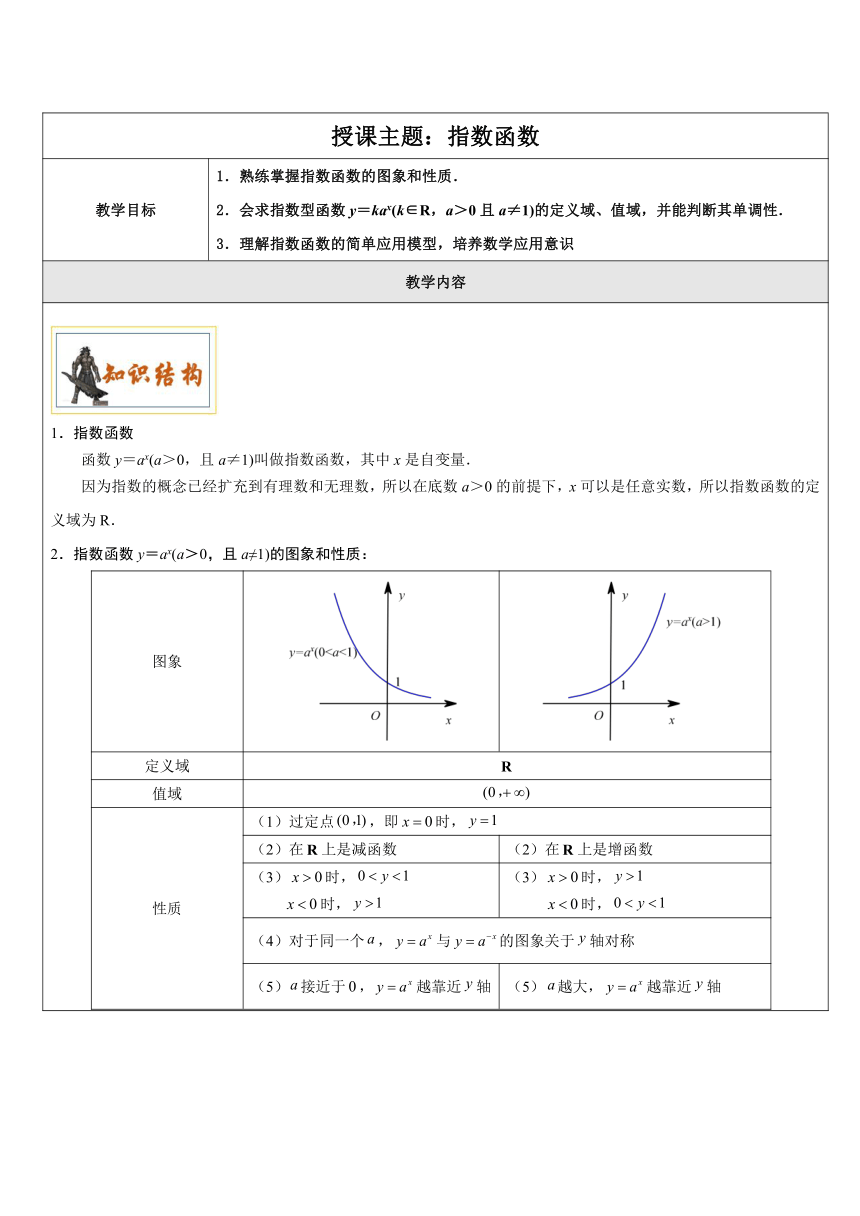
1.指数函数函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量.因为指数的概念已经扩充到有理数和无理数,所以在底数a>0的前提下,x可以是任意实数,所以指数函数的定义域为R.2.指数函数y=ax(a>0,且a≠1)的图象和性质:图象定义域值域性质(1)过定点,即时,(2)在上是减函数(2)在上是增函数(3)时,时,(3)时,时,(4)对于同一个,与的图象关于轴对称(5)接近于,越靠近轴(5)越大,越靠近轴题型一 指数函数概念的理解和应用
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
例1
点评:判断一个函数是否为指数函数,只需判定其解析式是否符合y=ax(a>0且a≠1)这一形式,即底数a为不等于1的正常数,指数只能是x,且ax的系数为1.
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
巩
固 下列函数是指数函数的是( )A.y=2x+1
B.y=x3C.y=3-x
D.y=3·2x答案:C题型二 求指数函数的定义域与值域
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
例2 求下列函数的定义域与值域:点评:函数y=af(x)的定义域、值域的求法.(1)函数y=af(x)的定义域与y=f(x)的定义域相同.(2)函数y=af(x)的值域的求法如下:①换元,令t=f(x);②求t=f(x)的定义域D;③求t=f(x)的值域M;④利用y=at的单调性求y=at,t∈M的值域.
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
巩
固 求下列函数的定义域和值域:题型三 指数函数的图象的应用
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
例3 下图是指数函数:①y=ax(a>0,且a≠1),②y=bx(b>0,且b≠1),③y=cx(c>0,且c≠1),④y=dx(d>0,且d≠1)的图象,则a,b,c,d与1的大小关系为( )A.a<b<1<c<d B.b<a<1<d<cC.b<a<1<c<d
D.a<b<1<d<c解析:法一:在①②中底数小于1且大于零,在y轴右侧,底数越小,图象向下越靠近x轴,故有b<a,在③④中底数大于1,在y轴右边,底数越大图象向上越靠近y轴,故有d<c.法二:设直线x=1与①、②、③、④的图象分别交于点A,B,C,D(如上图),则其坐标依次为(1,a),(1,b),(1,c),(1,d),由图象观察可得c>d>1>a>b.答案:B点评:1.指数函数的图象随底数变化的规律(1)无论指数函数的底数a如何变化,指数函数y=ax的图象都与直线x=1相交于点(1,a).由图象可知:在y轴右侧,图象从下到上相应的底数由小变大.(2)指数函数的底数与图象间的关系可概括为:在第一象限内,图高则底大.2.指数函数图象问题的处理方法(1)抓住图象上的特殊点,如指数函数的图象过定点(0,1);(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移);(3)利用函数的奇偶性与单调性.
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
巩
固 图中的曲线是指数函数的图象,已知取四个值,则相应于曲线的依次为_______________.答案:题型四 利用指数函数的单调性比较大小
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
例4 比较下列各组数的大小:
点评:比较幂的大小的方法
(1)对于底数相同,但指数不同的幂的大小比较,可以利用指数函数的单调性来判断.
(2)对于底数不同,指数相同的幂的大小比较,可利用指数函数的图象的变化规律来判断.
(3)对于底数不同且指数不同的幂的大小比较,则应通过中间值来比较.
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
巩
固 比较下列各组数的大小:题型五 求指数函数的单调区间例5 确定函数的单调区间,并对其加以证明.点评:1.关于指数型函数y=af(x)(a>0,且a≠1)的单调性由两点决定,一是底数a>1还是0<a<1;二是f(x)的单调性,它由两个函数y=au,u=f(x)复合而成.2.y=f(u),u=g(x),列函数y=f[g(x)]的单调性有如下特点:u=g(x)y=f(u)y=f[g(x)]增增增增减减减增减减减增3.求复合函数的单调区间,首先求出函数的定义域,然后把函数分解成y=f(u),u=φ(x),通过考查f(u)和φ(x)的单调性,求出y=f[φ(x)]的单调性.巩
固 已知a>0且a≠1,讨论函数的单调性.
题型六 解简单的指数不等式例6 已知不等式a2x+1≤ax-5(a>0,且a≠1),试求x的取值范围.点评:形如ax>ay的不等式,可借助y=ax的单调性求解.如果a的值不确定,需分0<a<1和a>1讨论.巩
固 已知集合,,则等于(
)A.{-1,1} B.{-1}
C.{0}
D.{-1,0}题型七 根据指数函数的图象研究其定义域、值域例7 求函数的定义域、值域,并作出图像.点评:含绝对值问题注意讨论去绝对值,指数函数定义域、值域相关问题注意利用函数的图象.巩
固 画出函数y=2|x+1|的图象.
分析:通过分类讨论可去掉绝对值号,变为分段函数,进而作出图象.另外,也可把函数y=2|x+1|看作由y=2|x|左移一个单位得到,而y=2|x|的图象,可由y=2x的图经对称变换得到.解析:法一:由函数解析式可得法二:故先作出y=2x(x≥0)的图象,再作关于y轴对称,y=2|x|的图象,再将y=2|x|的图象左移一个单位即可得到y=2|x+1|的图象.点评:函数y=ax的图象与y=a-x的图象关于y轴对称,y=ax的图象与y=-ax的图象关于x轴对称,函数y=ax的图象与y=-a-x的图象关于坐标原点对称.A组1.
指数函数y=f(x)的图象经过点(2,4),那么f(2)·f(4)的值为( )A.64
B.256
C.8
D.162.设,则有(
)A.y3>y1>y2
B.y2>y1>y3C.y1>y2>y3
D.y1>y3>y23.函数的定义域为___________;值域为____________.答案:;B组1.函数f(x)=的定义域是( )A.(-∞,0)
B.[0,+∞)C.(-∞,0]
D.(-∞,+∞)解析:由1-2x≥0,得2x≤1,由指数函数y=2x的性质可知x≤0.答案:C2.一种细胞在分裂时由一个分裂成两个,两个分裂成四个,四个分裂成八个,……每天分裂一次,现在将一个该细胞放入一个容器,发现经过10天就可充满整个容器,则当细胞分裂到充满容器的一半时需要的天数是( )A.5天
B.6天C.8天
D.9天答案:D 3.若0<a<1,b<-2,则函数y=ax+b的图象一定不经过( )A.第一象限
B.第二象限C.第三象限
D.第四象限答案:A4.函数=y的定义域是________.C组1.已知a,b>1,f(x)=ax,g(x)=bx,当f(x1)=g(x2)=2时,
有x1>x2,则a,b的大小关系是( )A.a=b
B.a>bC.a<b
D.不能确定解析:∵a>1,b>1,由图示知b>a.答案:C2.定义运算,例如,则函数的值域为______________.3.若函数f(x)=ax-1+3恒过定点P,试求点P的坐标.分析:研究f(x)=ax的图象和f(x)=ax-1+3图象的关系,由指数函数恒过(0,1)点推导.解析:将指数函数y=ax(a>0,且a≠1)的图象沿x轴右移一个单位,再沿y轴向上平移3个单位,即可得到y=ax-1+3的图象,因为y=ax的图象恒过(0,1),故相应的y=ax-1+3恒过定点(1,4).4.的最大、最小值.
A组1.
函数f(x)=3-x-1的值域是( )A.R
B.(0,+∞)C.(-1,+∞)
D.[0,+∞)答案:CA.
B.
C.
D.
B组1.已知指数函数y=ax(a>0,且a≠1)在[0,1]上的最大值与最小值的和为3,则a等于( )A.
B.2
C.4
D.解析:∵指数函数在其定义域内是单调函数,∴端点处取得最大、小值,∴a0+a=3,故a=2.答案:B2.下列不等关系中,正确的是( )A.eq
\f(2,3)<1<
B.eq
\f(1,3)<eq
\f(2,3)<1C.1<eq
\f(1,3)<eq
\f(2,3)
D.eq
\f(2,3)<eq
\f(1,3)<13.函数f(x)=ax(a>0且a≠1),对于任意实数x,y都有( )A.f(xy)=f(x)f(y)
B.f(xy)=f(x)+f(y)C.f(x+y)=f(x)f(y)
D.f(x+y)=f(x)+f(y)解析:f(x+y)=ax+y=axay=f(x)f(y).故选C.答案:C4.将函数y=2x的图象先向右平移1个单位,再向上平移2个单位可得到函数__________的图象.答案:y=2x-1+25.函数y=x-2x在区间[-1,
1]上的最大值为________.解析:∵y=x-2x在区间[-1,1]上是单调减函数,∴当x=-1时,有最大值为.答案:C组1.函数y=|2-x-2|的图象是( )答案:D2.已知(a2+a+2)x>(a2+a+2)1-x,则x的取值范围为( )A.(-∞,1)
B.C.(0,2)
D.R解析:∵a2+a+2=2+>1,∴由题设知x>1-x,解得x>.答案:B3.已知函数f(x)=a-,若f(x)为奇函数,则a=__________.解析:∵f(-x)=a-=a-,∵f(x)为奇函数,∴f(-x)=-f(x),∴a-=-a?2a=1?a=.答案:4.解析:令t=x2-4x+3,则y=3t.(1)当x∈[2,+∞)时,t=x2-4x+3是x的增函数,而y=3t是t的增函数
,故y=3x2-4x+3的单调递增区间是[2,+∞).(2)当x∈(-∞,2]时,t=x2-4x+3是x的减函数,而y=3t是t的增函数,故y=3x2-4x+3的单调递减区间是(-∞,2].
PAGE
教学目标
1.熟练掌握指数函数的图象和性质.2.会求指数型函数y=kax(k∈R,a>0且a≠1)的定义域、值域,并能判断其单调性.3.理解指数函数的简单应用模型,培养数学应用意识
教学内容
1.指数函数函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量.因为指数的概念已经扩充到有理数和无理数,所以在底数a>0的前提下,x可以是任意实数,所以指数函数的定义域为R.2.指数函数y=ax(a>0,且a≠1)的图象和性质:图象定义域值域性质(1)过定点,即时,(2)在上是减函数(2)在上是增函数(3)时,时,(3)时,时,(4)对于同一个,与的图象关于轴对称(5)接近于,越靠近轴(5)越大,越靠近轴题型一 指数函数概念的理解和应用
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
例1
点评:判断一个函数是否为指数函数,只需判定其解析式是否符合y=ax(a>0且a≠1)这一形式,即底数a为不等于1的正常数,指数只能是x,且ax的系数为1.
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
巩
固 下列函数是指数函数的是( )A.y=2x+1
B.y=x3C.y=3-x
D.y=3·2x答案:C题型二 求指数函数的定义域与值域
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
例2 求下列函数的定义域与值域:点评:函数y=af(x)的定义域、值域的求法.(1)函数y=af(x)的定义域与y=f(x)的定义域相同.(2)函数y=af(x)的值域的求法如下:①换元,令t=f(x);②求t=f(x)的定义域D;③求t=f(x)的值域M;④利用y=at的单调性求y=at,t∈M的值域.
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
巩
固 求下列函数的定义域和值域:题型三 指数函数的图象的应用
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
例3 下图是指数函数:①y=ax(a>0,且a≠1),②y=bx(b>0,且b≠1),③y=cx(c>0,且c≠1),④y=dx(d>0,且d≠1)的图象,则a,b,c,d与1的大小关系为( )A.a<b<1<c<d B.b<a<1<d<cC.b<a<1<c<d
D.a<b<1<d<c解析:法一:在①②中底数小于1且大于零,在y轴右侧,底数越小,图象向下越靠近x轴,故有b<a,在③④中底数大于1,在y轴右边,底数越大图象向上越靠近y轴,故有d<c.法二:设直线x=1与①、②、③、④的图象分别交于点A,B,C,D(如上图),则其坐标依次为(1,a),(1,b),(1,c),(1,d),由图象观察可得c>d>1>a>b.答案:B点评:1.指数函数的图象随底数变化的规律(1)无论指数函数的底数a如何变化,指数函数y=ax的图象都与直线x=1相交于点(1,a).由图象可知:在y轴右侧,图象从下到上相应的底数由小变大.(2)指数函数的底数与图象间的关系可概括为:在第一象限内,图高则底大.2.指数函数图象问题的处理方法(1)抓住图象上的特殊点,如指数函数的图象过定点(0,1);(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移);(3)利用函数的奇偶性与单调性.
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
巩
固 图中的曲线是指数函数的图象,已知取四个值,则相应于曲线的依次为_______________.答案:题型四 利用指数函数的单调性比较大小
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
例4 比较下列各组数的大小:
点评:比较幂的大小的方法
(1)对于底数相同,但指数不同的幂的大小比较,可以利用指数函数的单调性来判断.
(2)对于底数不同,指数相同的幂的大小比较,可利用指数函数的图象的变化规律来判断.
(3)对于底数不同且指数不同的幂的大小比较,则应通过中间值来比较.
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
INCLUDEPICTURE
"F:\\源文件\\人教B版\\左括.TIF"
\
MERGEFORMATINET
巩
固 比较下列各组数的大小:题型五 求指数函数的单调区间例5 确定函数的单调区间,并对其加以证明.点评:1.关于指数型函数y=af(x)(a>0,且a≠1)的单调性由两点决定,一是底数a>1还是0<a<1;二是f(x)的单调性,它由两个函数y=au,u=f(x)复合而成.2.y=f(u),u=g(x),列函数y=f[g(x)]的单调性有如下特点:u=g(x)y=f(u)y=f[g(x)]增增增增减减减增减减减增3.求复合函数的单调区间,首先求出函数的定义域,然后把函数分解成y=f(u),u=φ(x),通过考查f(u)和φ(x)的单调性,求出y=f[φ(x)]的单调性.巩
固 已知a>0且a≠1,讨论函数的单调性.
题型六 解简单的指数不等式例6 已知不等式a2x+1≤ax-5(a>0,且a≠1),试求x的取值范围.点评:形如ax>ay的不等式,可借助y=ax的单调性求解.如果a的值不确定,需分0<a<1和a>1讨论.巩
固 已知集合,,则等于(
)A.{-1,1} B.{-1}
C.{0}
D.{-1,0}题型七 根据指数函数的图象研究其定义域、值域例7 求函数的定义域、值域,并作出图像.点评:含绝对值问题注意讨论去绝对值,指数函数定义域、值域相关问题注意利用函数的图象.巩
固 画出函数y=2|x+1|的图象.
分析:通过分类讨论可去掉绝对值号,变为分段函数,进而作出图象.另外,也可把函数y=2|x+1|看作由y=2|x|左移一个单位得到,而y=2|x|的图象,可由y=2x的图经对称变换得到.解析:法一:由函数解析式可得法二:故先作出y=2x(x≥0)的图象,再作关于y轴对称,y=2|x|的图象,再将y=2|x|的图象左移一个单位即可得到y=2|x+1|的图象.点评:函数y=ax的图象与y=a-x的图象关于y轴对称,y=ax的图象与y=-ax的图象关于x轴对称,函数y=ax的图象与y=-a-x的图象关于坐标原点对称.A组1.
指数函数y=f(x)的图象经过点(2,4),那么f(2)·f(4)的值为( )A.64
B.256
C.8
D.162.设,则有(
)A.y3>y1>y2
B.y2>y1>y3C.y1>y2>y3
D.y1>y3>y23.函数的定义域为___________;值域为____________.答案:;B组1.函数f(x)=的定义域是( )A.(-∞,0)
B.[0,+∞)C.(-∞,0]
D.(-∞,+∞)解析:由1-2x≥0,得2x≤1,由指数函数y=2x的性质可知x≤0.答案:C2.一种细胞在分裂时由一个分裂成两个,两个分裂成四个,四个分裂成八个,……每天分裂一次,现在将一个该细胞放入一个容器,发现经过10天就可充满整个容器,则当细胞分裂到充满容器的一半时需要的天数是( )A.5天
B.6天C.8天
D.9天答案:D 3.若0<a<1,b<-2,则函数y=ax+b的图象一定不经过( )A.第一象限
B.第二象限C.第三象限
D.第四象限答案:A4.函数=y的定义域是________.C组1.已知a,b>1,f(x)=ax,g(x)=bx,当f(x1)=g(x2)=2时,
有x1>x2,则a,b的大小关系是( )A.a=b
B.a>bC.a<b
D.不能确定解析:∵a>1,b>1,由图示知b>a.答案:C2.定义运算,例如,则函数的值域为______________.3.若函数f(x)=ax-1+3恒过定点P,试求点P的坐标.分析:研究f(x)=ax的图象和f(x)=ax-1+3图象的关系,由指数函数恒过(0,1)点推导.解析:将指数函数y=ax(a>0,且a≠1)的图象沿x轴右移一个单位,再沿y轴向上平移3个单位,即可得到y=ax-1+3的图象,因为y=ax的图象恒过(0,1),故相应的y=ax-1+3恒过定点(1,4).4.的最大、最小值.
A组1.
函数f(x)=3-x-1的值域是( )A.R
B.(0,+∞)C.(-1,+∞)
D.[0,+∞)答案:CA.
B.
C.
D.
B组1.已知指数函数y=ax(a>0,且a≠1)在[0,1]上的最大值与最小值的和为3,则a等于( )A.
B.2
C.4
D.解析:∵指数函数在其定义域内是单调函数,∴端点处取得最大、小值,∴a0+a=3,故a=2.答案:B2.下列不等关系中,正确的是( )A.eq
\f(2,3)<1<
B.eq
\f(1,3)<eq
\f(2,3)<1C.1<eq
\f(1,3)<eq
\f(2,3)
D.eq
\f(2,3)<eq
\f(1,3)<13.函数f(x)=ax(a>0且a≠1),对于任意实数x,y都有( )A.f(xy)=f(x)f(y)
B.f(xy)=f(x)+f(y)C.f(x+y)=f(x)f(y)
D.f(x+y)=f(x)+f(y)解析:f(x+y)=ax+y=axay=f(x)f(y).故选C.答案:C4.将函数y=2x的图象先向右平移1个单位,再向上平移2个单位可得到函数__________的图象.答案:y=2x-1+25.函数y=x-2x在区间[-1,
1]上的最大值为________.解析:∵y=x-2x在区间[-1,1]上是单调减函数,∴当x=-1时,有最大值为.答案:C组1.函数y=|2-x-2|的图象是( )答案:D2.已知(a2+a+2)x>(a2+a+2)1-x,则x的取值范围为( )A.(-∞,1)
B.C.(0,2)
D.R解析:∵a2+a+2=2+>1,∴由题设知x>1-x,解得x>.答案:B3.已知函数f(x)=a-,若f(x)为奇函数,则a=__________.解析:∵f(-x)=a-=a-,∵f(x)为奇函数,∴f(-x)=-f(x),∴a-=-a?2a=1?a=.答案:4.解析:令t=x2-4x+3,则y=3t.(1)当x∈[2,+∞)时,t=x2-4x+3是x的增函数,而y=3t是t的增函数
,故y=3x2-4x+3的单调递增区间是[2,+∞).(2)当x∈(-∞,2]时,t=x2-4x+3是x的减函数,而y=3t是t的增函数,故y=3x2-4x+3的单调递减区间是(-∞,2].
PAGE
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
