1.4解直角三角形课时训练(Word版 含答案)
文档属性
| 名称 | 1.4解直角三角形课时训练(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 913.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-17 00:00:00 | ||
图片预览


文档简介
1.4解直角三角形课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
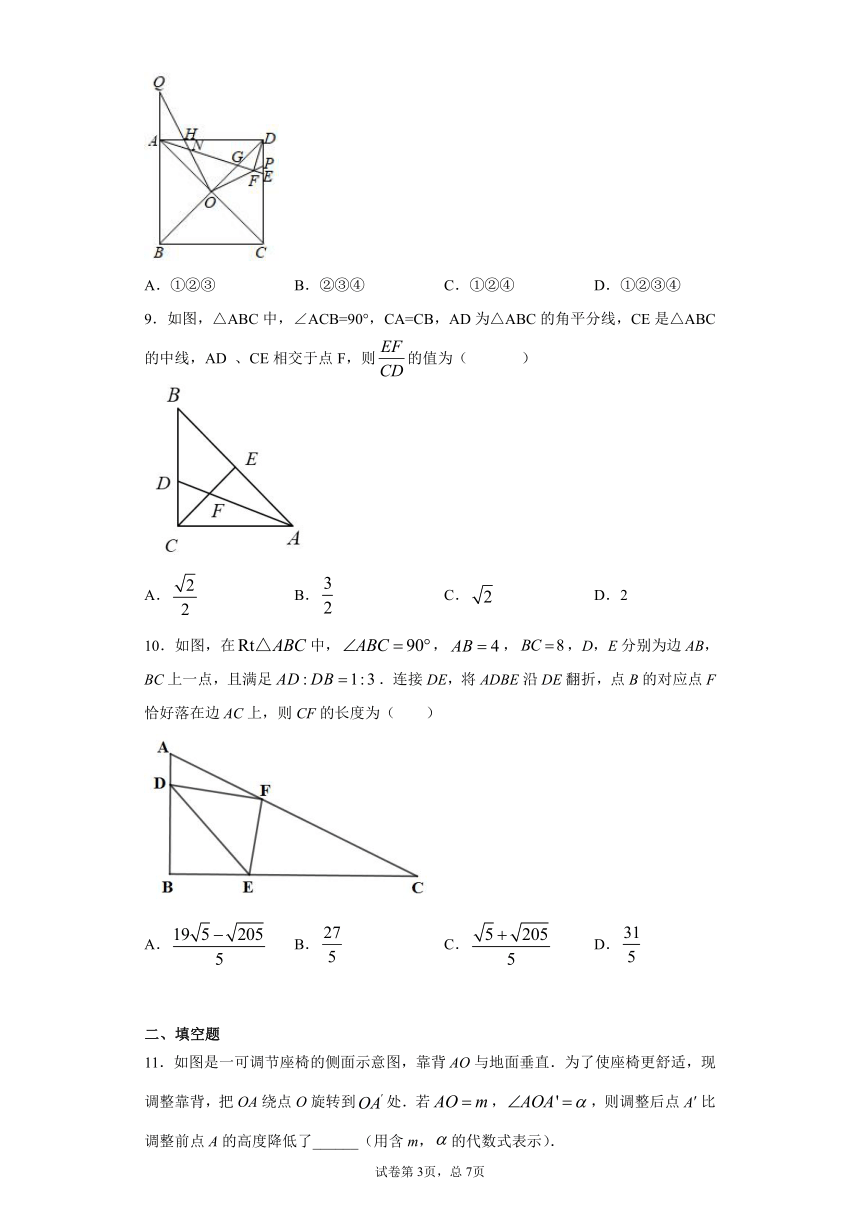
1.如图,在中,,则等于( )
A. B. C. D.
2.小明沿着坡度为的山坡向下走了,则他下降了( )
A. B. C. D.
3.如图,在中,平分,交于点,交于点,且交于点,若,则的值为( )
A. B. C. D.
4.如图,中,,,,若,则的长为( )
A.6 B. C.7.5 D.10
5.如图,与都是等腰三角形,且,,若,则与的面积比为( )
A. B. C. D.
6.如图在一笔直的海岸线l上有相距3km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离是( )
A.km B.km C.km D.km
7.如图,中,,点D在上,.若,,则的长度为( )
A. B. C. D.4
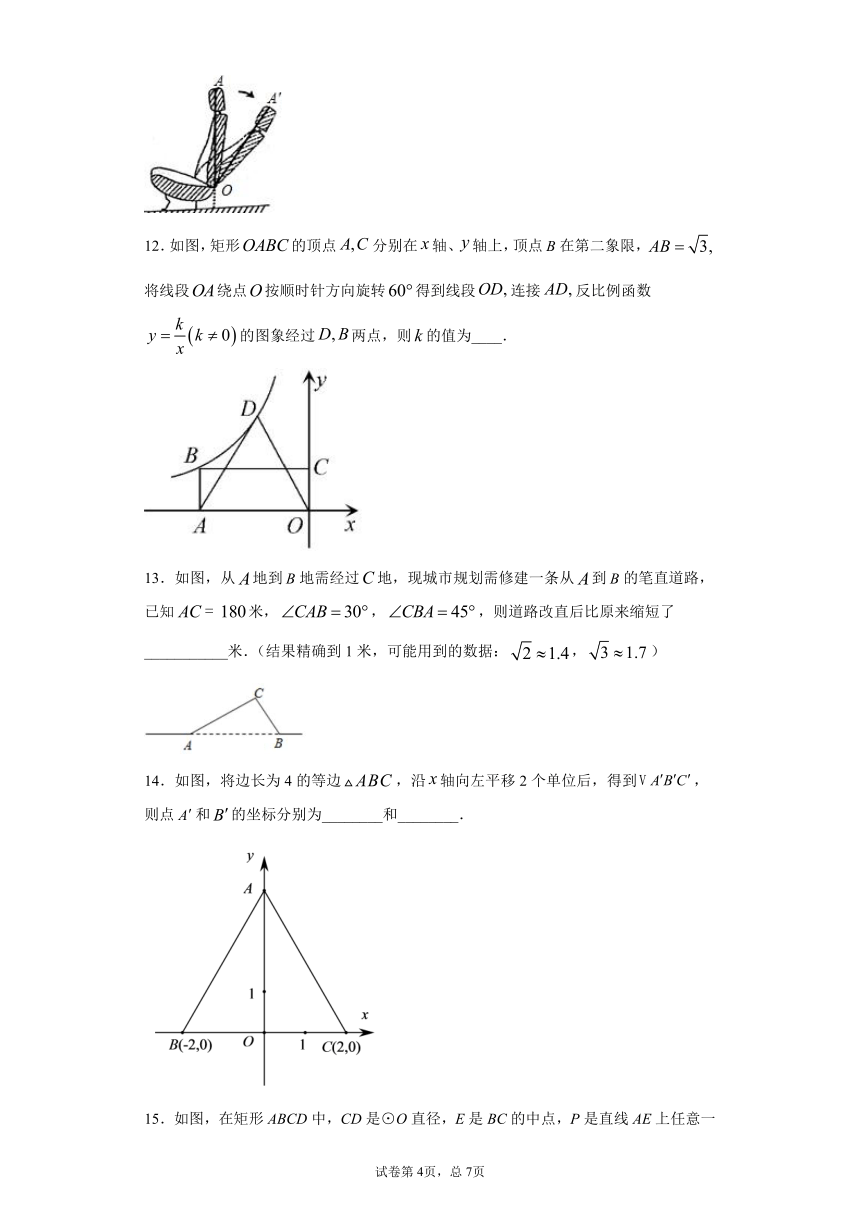
8.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E在DC边上,且CE=2DE,连接AE交BD于点G,过点D作DF⊥AE,连接OF并延长,交DC于点P,过点O作OQ⊥OP分别交AE、AD于点N、H,交BA的延长线于点Q,现给出下列结论:①∠AFO=45°;②OG=DG;③DP2=NH?OH;④sin∠AQO=;其中正确的结论有( )
A.①②③ B.②③④ C.①②④ D.①②③④
9.如图,△ABC中,∠ACB=90°,CA=CB,AD为△ABC的角平分线,CE是△ABC的中线,AD 、CE相交于点F,则的值为( )
A. B. C. D.2
10.如图,在中,,,,D,E分别为边AB,BC上一点,且满足.连接DE,将ADBE沿DE翻折,点B的对应点F恰好落在边AC上,则CF的长度为( )
A. B. C. D.
二、填空题
11.如图是一可调节座椅的侧面示意图,靠背AO与地面垂直.为了使座椅更舒适,现调整靠背,把OA绕点O旋转到处.若,,则调整后点比调整前点A的高度降低了______(用含m,的代数式表示).
12.如图,矩形的顶点分别在轴、轴上,顶点在第二象限,将线段绕点按顺时针方向旋转得到线段连接反比例函数的图象经过两点,则的值为____.
13.如图,从地到地需经过地,现城市规划需修建一条从到的笔直道路,已知米,,,则道路改直后比原来缩短了___________米.(结果精确到1米,可能用到的数据:,)
14.如图,将边长为4的等边,沿轴向左平移2个单位后,得到,则点和的坐标分别为________和________.
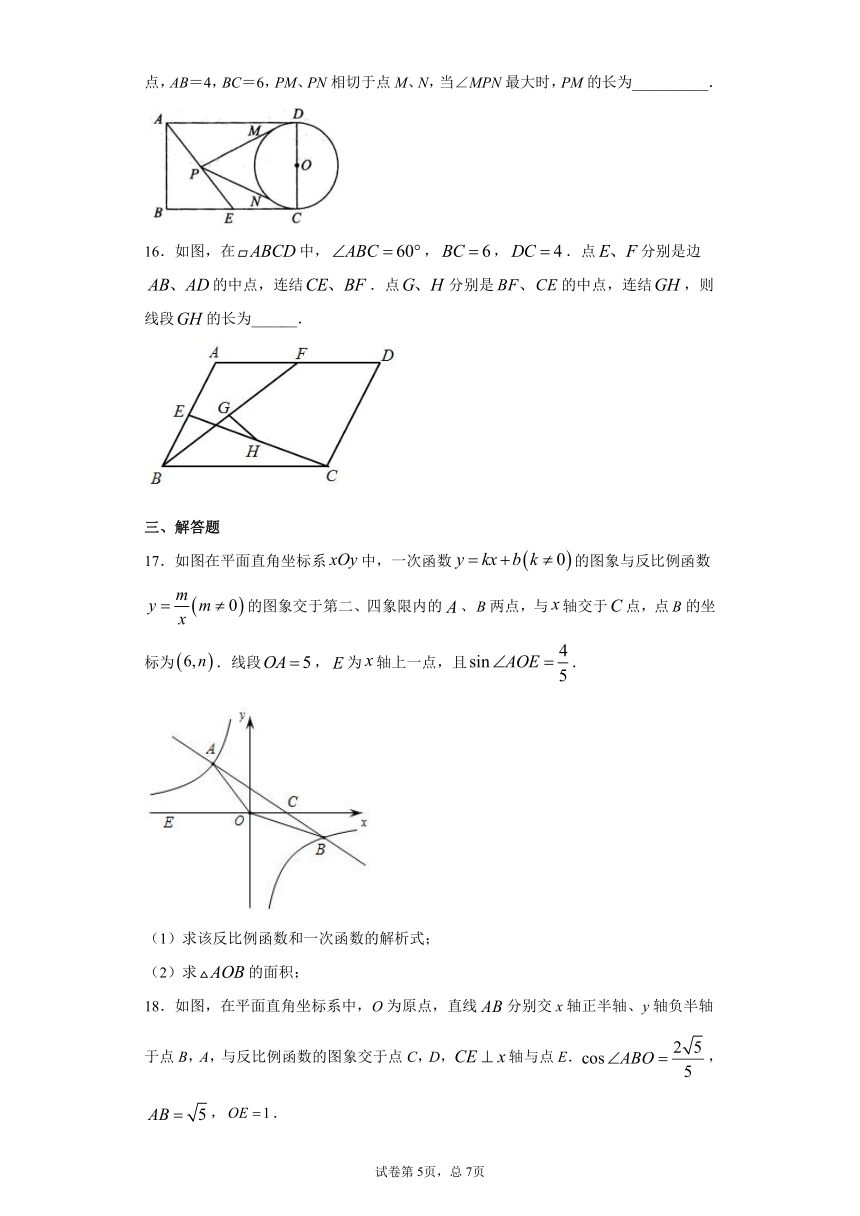
15.如图,在矩形ABCD中,CD是⊙O直径,E是BC的中点,P是直线AE上任意一点,AB=4,BC=6,PM、PN相切于点M、N,当∠MPN最大时,PM的长为__________.
16.如图,在中,,,.点分别是边的中点,连结.点分别是的中点,连结,则线段的长为______.
三、解答题
17.如图在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的、两点,与轴交于点,点的坐标为.线段,为轴上一点,且.
(1)求该反比例函数和一次函数的解析式;
(2)求的面积;
18.如图,在平面直角坐标系中,O为原点,直线分别交x轴正半轴、y轴负半轴于点B,A,与反比例函数的图象交于点C,D,轴与点E.,,.
(1)求直线和反比例函数的解析式;
(2)求的值.
19.已知:在矩形中,连接,过点作,交于点,交于点.
(1)如图1,若.
①求证:;
②连接,求证:.
(2)如图2,若,求的值.
20.我南海巡逻船接到有人落水求救信号,如图,巡逻船观测到,同时,巡逻船观测到,,两巡逻船相距海里,求此时巡逻船与落水人之间的距离是多少海里?(结果精确到海里.参考数据:,,,)
参考答案
1.C
2.A
3.C
4.B
5.C
6.C
7.B
8.D
9.A
10.A
11.
12.
13.63.
14.
15.
16.
17.(1),;(2)9
【详解】
解:(1)过作轴交轴于,
∴,,
∴,
∴,
∴,
将代入,得,
∴反比例函数的解析式为,
将代入,得,
∴,
将和分别代入,
得,解得,
∴直线解析式:;
(2)在直线中,令,则有,解得,
∴,即,
∴;
同理,则.
18.(1),;(2)
【详解】
解:(1)∵cos∠ABO=,AB=,
∴OB=2,
根据勾股定理得:OA=1,
∴点B(2,0),点A(0,-1),
设直线AB的表达式为y=kx+b,
则,解得:,
∴直线AB:,
∵OE=1,
∴点C的横坐标为-1,代入直线AB表达式,
得,y=,
∴点C的坐标为(-1,),
-1×()=,
∴反比例函数表达式为:;
(2)过点O作AB边上的高OF,
∵AB×OF=OA×OB,
∴OF==,
∵OE=1,CE=,
∴OC==,CF==,
∴tan∠OCD=.
19.(1)①见解析;②见解析;(2).
【详解】
(1)证明:①如图,在矩形中,∠DAB=∠ADC=90°,
∴∠1+∠EDC=90°,
又∵,
∴∠2+∠EDC=90°,
∴,
∵,
∴,
∴,
又∵AB=CD,
∴,
∴.
②证明:如解图2,延长、,交于点.
∵在矩形中,AD//BC,
∴,
在和中,
∴≌,
∴,
故中,.
由(1)可知,
∴,
∴,
(2)∵,,
∴,
又∵∠ADF=∠DCA,
∴,
∴,
在Rt△ADF中,,
∴,
∴,
又∵在矩形中,AB//CD,
∴,
∴.
20.52海里
【详解】
解:如图,过点作,垂足为,
设海里.
在中,
,
在中,
,
,
,解得.
海里
,
(海里).
巡逻船与落水人的距离约为海里.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,则等于( )
A. B. C. D.
2.小明沿着坡度为的山坡向下走了,则他下降了( )
A. B. C. D.
3.如图,在中,平分,交于点,交于点,且交于点,若,则的值为( )
A. B. C. D.
4.如图,中,,,,若,则的长为( )
A.6 B. C.7.5 D.10
5.如图,与都是等腰三角形,且,,若,则与的面积比为( )
A. B. C. D.
6.如图在一笔直的海岸线l上有相距3km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离是( )
A.km B.km C.km D.km
7.如图,中,,点D在上,.若,,则的长度为( )
A. B. C. D.4
8.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E在DC边上,且CE=2DE,连接AE交BD于点G,过点D作DF⊥AE,连接OF并延长,交DC于点P,过点O作OQ⊥OP分别交AE、AD于点N、H,交BA的延长线于点Q,现给出下列结论:①∠AFO=45°;②OG=DG;③DP2=NH?OH;④sin∠AQO=;其中正确的结论有( )
A.①②③ B.②③④ C.①②④ D.①②③④
9.如图,△ABC中,∠ACB=90°,CA=CB,AD为△ABC的角平分线,CE是△ABC的中线,AD 、CE相交于点F,则的值为( )
A. B. C. D.2
10.如图,在中,,,,D,E分别为边AB,BC上一点,且满足.连接DE,将ADBE沿DE翻折,点B的对应点F恰好落在边AC上,则CF的长度为( )
A. B. C. D.
二、填空题
11.如图是一可调节座椅的侧面示意图,靠背AO与地面垂直.为了使座椅更舒适,现调整靠背,把OA绕点O旋转到处.若,,则调整后点比调整前点A的高度降低了______(用含m,的代数式表示).
12.如图,矩形的顶点分别在轴、轴上,顶点在第二象限,将线段绕点按顺时针方向旋转得到线段连接反比例函数的图象经过两点,则的值为____.
13.如图,从地到地需经过地,现城市规划需修建一条从到的笔直道路,已知米,,,则道路改直后比原来缩短了___________米.(结果精确到1米,可能用到的数据:,)
14.如图,将边长为4的等边,沿轴向左平移2个单位后,得到,则点和的坐标分别为________和________.
15.如图,在矩形ABCD中,CD是⊙O直径,E是BC的中点,P是直线AE上任意一点,AB=4,BC=6,PM、PN相切于点M、N,当∠MPN最大时,PM的长为__________.
16.如图,在中,,,.点分别是边的中点,连结.点分别是的中点,连结,则线段的长为______.
三、解答题
17.如图在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的、两点,与轴交于点,点的坐标为.线段,为轴上一点,且.
(1)求该反比例函数和一次函数的解析式;
(2)求的面积;
18.如图,在平面直角坐标系中,O为原点,直线分别交x轴正半轴、y轴负半轴于点B,A,与反比例函数的图象交于点C,D,轴与点E.,,.
(1)求直线和反比例函数的解析式;
(2)求的值.
19.已知:在矩形中,连接,过点作,交于点,交于点.
(1)如图1,若.
①求证:;
②连接,求证:.
(2)如图2,若,求的值.
20.我南海巡逻船接到有人落水求救信号,如图,巡逻船观测到,同时,巡逻船观测到,,两巡逻船相距海里,求此时巡逻船与落水人之间的距离是多少海里?(结果精确到海里.参考数据:,,,)
参考答案
1.C
2.A
3.C
4.B
5.C
6.C
7.B
8.D
9.A
10.A
11.
12.
13.63.
14.
15.
16.
17.(1),;(2)9
【详解】
解:(1)过作轴交轴于,
∴,,
∴,
∴,
∴,
将代入,得,
∴反比例函数的解析式为,
将代入,得,
∴,
将和分别代入,
得,解得,
∴直线解析式:;
(2)在直线中,令,则有,解得,
∴,即,
∴;
同理,则.
18.(1),;(2)
【详解】
解:(1)∵cos∠ABO=,AB=,
∴OB=2,
根据勾股定理得:OA=1,
∴点B(2,0),点A(0,-1),
设直线AB的表达式为y=kx+b,
则,解得:,
∴直线AB:,
∵OE=1,
∴点C的横坐标为-1,代入直线AB表达式,
得,y=,
∴点C的坐标为(-1,),
-1×()=,
∴反比例函数表达式为:;
(2)过点O作AB边上的高OF,
∵AB×OF=OA×OB,
∴OF==,
∵OE=1,CE=,
∴OC==,CF==,
∴tan∠OCD=.
19.(1)①见解析;②见解析;(2).
【详解】
(1)证明:①如图,在矩形中,∠DAB=∠ADC=90°,
∴∠1+∠EDC=90°,
又∵,
∴∠2+∠EDC=90°,
∴,
∵,
∴,
∴,
又∵AB=CD,
∴,
∴.
②证明:如解图2,延长、,交于点.
∵在矩形中,AD//BC,
∴,
在和中,
∴≌,
∴,
故中,.
由(1)可知,
∴,
∴,
(2)∵,,
∴,
又∵∠ADF=∠DCA,
∴,
∴,
在Rt△ADF中,,
∴,
∴,
又∵在矩形中,AB//CD,
∴,
∴.
20.52海里
【详解】
解:如图,过点作,垂足为,
设海里.
在中,
,
在中,
,
,
,解得.
海里
,
(海里).
巡逻船与落水人的距离约为海里.
